一類變指數退化拋物方程的解

許文彬

(集美大學理學院，福建 廈門 361021)

0 引言

考慮如下帶有變指數增長階的非線性方程

(1)

v(x,0)=v0(x),x∈Ω

(2)

是需要的。但如果b(x,t)|x∈?Ω=0，則不需要一般的邊界條件v(x,t)=0,(x,t)∈?Ω×(0,T)。

當p(x,t)=p是常數時，方程(1)就是經典的具有對流項的非牛頓流方程，對此已經有許多的研究成果[1-9]。當b(x,t)≡1及gi=0時，方程(1)是電流變方程，其特征就是具有變指數p(x,t)增長階。21世紀以來，較多的研究者對該方程進行了研究[10-15]。

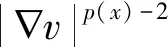
b(x,t)>0,x∈Ω,b(x,t)=0,x∈?Ω。

(3)

本文借鑒了文獻[16-20]的一些經驗，但本文的擴散系數b(x,t)和變指數p(z,t)均依賴于時間變量t，所以要克服時間變量t所帶來的一些本質的不同和困難。

1 定義和引理

定義2W1,p(x)(Ω)空間W1,p(x)(Ω)={u∈Lp(x)(Ω):|?u|∈Lp(x)(Ω)}具有范數|u|W1,p(x)=|u|Lp(x)(Ω)+|?u|Lp(x)(Ω),?u∈W1,p(x)(Ω)。

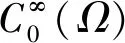
W1,p(x)(Ω)被稱為具有變指數的Sobolev空間，具有以下性質[21-22]。

現在考慮以下的初邊值問題

(4)

v(x,0)=v0(x),x∈Ω，(5)

v(x,t)=0,(x,t)∈?Ω×(0,T)。

(6)

則稱v(x,t)是問題(4)～(6)的弱解。

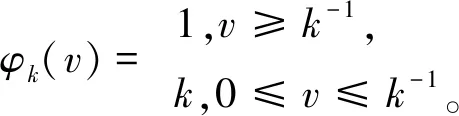
(7)

vk(x,t)=0，v(x,t)∈?Ω×(0,T),(8)

vk(x,0)=v0k(x)，x∈Ω,(9)

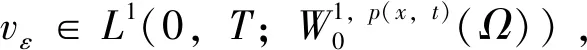
(10)

(11)

意義下成立，則稱b(x,t)是方程(1)具有初值條件(2)的弱解。

2 主要結果

(12)

則存在一方程(1)具有初值條件(2)的非負弱解b(x,t),這里c=c(T)表示常數與T有關。

(13)

由定理2，由于在Ω的內部函數b(x,t)>0,從式(13)可以看出，當u0(x)=v0(x)時，u(x,t)=v(x,t)幾乎處處成立，即解的唯一性成立。

3 定理1和定理2的證明

3.1 定理1的證明

取在定義4意義下問題(4)～(6)的非負弱解vε作為檢驗函數,則

(14)

因為，

(15)

根據gi(x,t)∈C1(QT),γi(s)∈C1(R)，所以由式(10)、(14)～(15)可推出

(16)

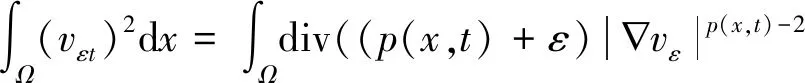
(17)

因為，有

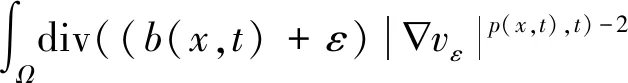
(18)

(19)

由式(17)～(19)可以推出

于是有

(20)

由式(16)和式(20)可以知道，vε→v于QT內幾乎處處收斂，于是γi(vε)→γi(v)于QT內也幾乎處處收斂。

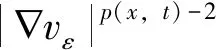
3.2 定理2的證明

取χ[τ,s](t)[u(x,t)-v(x,t)]ξλ(x,t)為檢驗函數，這里χ[τ,s]是區間[τ,s]?(0,T)特征函數,并記Qτs=Ω×(τ,s)。于是，有

?Qτs(u-v)ξλ(x,t)(?(u-v)/?t)dxdt=

(21)

首先，有

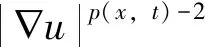
(22)

(23)

如果記Ω1t={x∈Ω:p(x,t)≥2},Ω2t={x∈Ω:p(x,t)<2}，因為u,v∈L∞，則有

(24)

利用H?lder不等式，可得

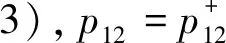
其次，有

(26)

由于β≥2p+，有

[b(x,t)-λ]β/p(x,t)-1|bxi|dxdt≤

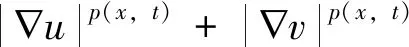
(28)

(29)

當p(x,t)≥2時，則q(x,t)<2。由β≥2，利用H?lder不等式，可以得到

c[?Qτs[b(x,t)(β-1)/(p(x,t)-1)-β/(2p(x,t)-1)]2/(2-q(x,t))dxdt]1/q22q1·

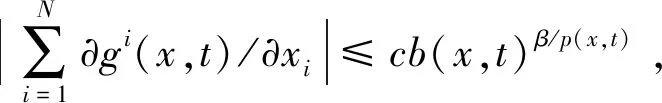
(31)

利用式(22)～(31)，在式(21)中令λ→0，可以推斷出，存在某個l≤1，使得

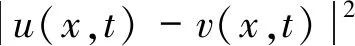
(32)

成立。

又

?Qτsb(x,t)β/p(x,t)(u-v)(?(u-v)/?t)dxdt=(1/2)?Qτsb(x,t)β/p(x,t)(?(u-v)2/?t)dxdt。

(33)

式(33)的一種可能情況是，對任意的s≥τ，有

(34)

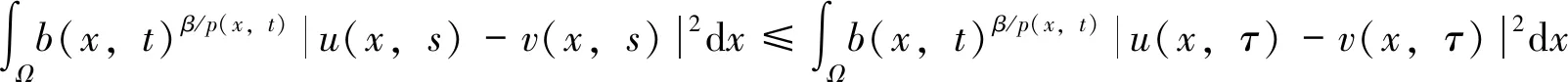
式(33)另一種可能是，存在s0≥τ，使得

(35)

結合式(32)～(33)，有

(36)

應用一個Gronwall不等式的推廣形式[28]，由式(36)可以推出，

這與式(35)矛盾，即式(35)是不可能發生的。意味著，對于任何的s,τ∈[0,T]，不等式(34)總成立。由τ的任意性，有

定理2得證。