一種凸極式磁阻型球形電機的結構設計

王群京，喬元忠，鞠魯峰，周睿，何競雄

(1.安徽大學 電氣工程與自動化學院，合肥 230601；2.安徽大學 高節能電機及控制技術國家地方聯合工程實驗室，合肥 230601；3.安徽大學 工業節電與電能質量控制協同創新中心，合肥 230601)

0 引 言

對于傳統的單軸電機而言，完成多自由度動作需要多臺電機進行組合控制，其機械系統效率低下，體積過大，控制繁瑣[1]。球形電機由于自身的結構特性可單獨完成三自由度運動，引起了人們的關注和研究，體積小、響應速度快、定位精確的優點使得其在機器人、攝像頭、汽車航天等領域擁有廣泛的應用前景[2]。

近年來，國內外學者對球形電機進行了大量的研究，并且設計分析了不同形式的球形電機。文獻[3]提出了永磁球形步進電動機，該電機轉子結構上均勻分布了40個永磁體，定子線圈共有16個，不考慮輸出軸的情況下，可以實現全角度旋轉，缺點是體積較大。文獻[4]基于定轉子磁場分析設計出一種新型永磁球形電機，轉子球表面的40個永磁體NS極交替分布，增大了電機的運動角，提高了電機輸出轉矩。文獻[5]把球形電機應用到了保形打印上(噴射印花機)，結合底座三軸運動可以實現6自由度運動，并且詳細探討了球形電機應用于保形打印的可行性。文獻[6]首次將Halbach陣列的永磁體引入到球形電機中，并分別采用解析法和有限元法對電機的磁場進行分析，該電機氣隙磁密近正弦分布。文獻[7]采用雙相正交繞組設計了一種新穎的殼式感應球形電機，并使用解析法和有限元法進行了磁場分析,該電機可以真正意義上不受結構限制實現三自由度旋轉。

為解決永磁類球形電機中出現的轉矩小、控制難的問題[8-9]，本文提出了一種新型磁阻型球形電機結構。電機中轉子結構得到了簡化，方便了磁場分析，為進一步精確確定電機參數、控制球形電機運動提供了理論依據。仿真結果證明了該設計方法是有效的和可行的。本文提出的電機的不同之處和顯著特點在于：1)轉子采用凸極式結構，減少了漏磁，并且將轉子中心掏空，減少了轉子23.59%的轉動慣量，使得電機有良好的動態響應；2)定子線圈含鐵心，降低了磁路中的磁勢消耗，提升了電機整體的動態性能，增加了轉矩輸出；3)電機的電磁轉矩與磁路中的磁阻大小相關，因此電磁轉矩方向與輸入電流的方向無關，而與轉子位置有關。

1 磁阻型球形電機結構與運動原理

1.1 電機結構

新型磁阻型球形電機的基本結構如圖1所示，電機本體由定子(球殼與定子鐵心)、轉子、線圈、轉軸四部分組成。電機的定子由2個電工純鐵材料制成的球殼合并而成，鐵心材料同樣使用電工純鐵，鐵心末端的極靴既可以增加定轉子相對接觸的有效面積，又可以防止線圈脫落。使用24個通電線圈可以滿足球形電機自旋運動、偏轉運動及側旋運動等復雜運動的要求，通電線圈分上中下3層，每層均勻分布8個，硅鋼片疊制成的轉子包裹于PC材料制成的輕質薄殼中。轉子齒每隔60°對稱分布，共有6個。

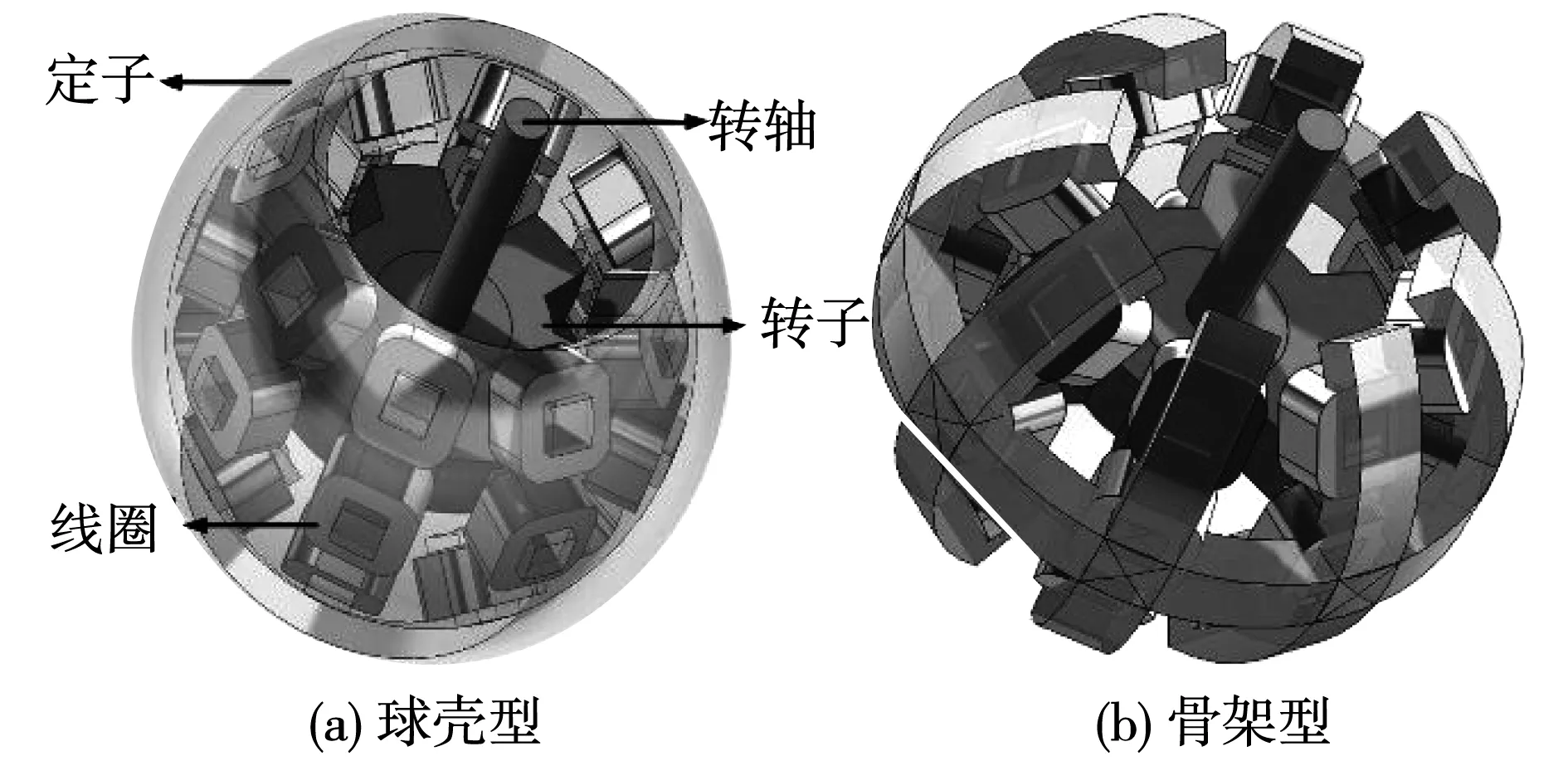
圖1 新型磁阻型球形電機結構

球形電機的結構特殊，對加工性能與制造工藝的要求較高，因此在本體設計階段必須保證現有的生產加工方式和工藝水平符合性能要求。根據文獻[10]，得知轉子結構可以通過沖片疊壓的方式制成，保證轉子齒表面整齊平滑，盡可能降低由于結構上的不對稱帶來的氣隙磁場畸變。本文中的球形電機繞組設計采用集中繞組的方案，便于線圈的繞制和繞組的安裝，查閱文獻[11]，考慮電磁線的安全載流量為8 A/mm2，為滿足電機轉動所需的電磁力矩輸出要求，滿足電機繞組與槽間的隔離絕緣要求，電磁線采用線徑為0.48 mm的漆包線。

1.2 自旋運動原理

磁阻型球形電機的繞組共有3層，目前，實現自旋運動的通電線圈組合方式有單個線圈、單對線圈、3個線圈等等，詳細內容見文獻[12]。為方便分析電機多自由度運動原理，將電機運動分解為自旋運動與傾斜運動進行描述。關于自旋運動，取電機橫剖面的定轉子進行概述。

如圖2(a)所示，在只考慮通電處于0°緯度角(使用類似地球的坐標系統)位置的線圈時，球形電機的自旋運動與8/6極開關磁阻電機運行原理相同，自旋運動的步進角[13]為

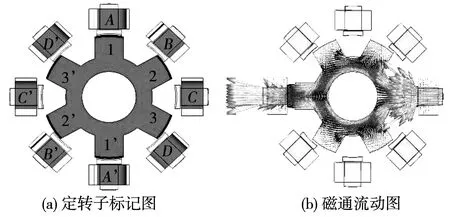
圖2 自旋運動示意圖

βstep=τr/m=360°/(mNr)。

(1)

式中:Nr為轉子極數；m為定子相數；τr為轉子極距。

圖2中的定子相A-A’與轉子齒1-1’重合(中心線對齊),此時A-A’-1-1’這條直線上磁阻最小，磁通的方向以此線為主流動，若給A-A’相通電，1-1’轉子齒受到徑向的電磁力，而切向電磁力可以視為0，轉子因而可以達到“自鎖”的狀態。反觀2-2’齒與B-B’相之間有15°的角度差，3-3’齒與D-D’相亦有15°的角度差，若僅給B-B’相通電，則轉子齒2-2’受到切向磁拉力逆時針向B-B’轉動。以圖3為起始位置，順序循環按照相序B-B’,C-C’,D-D’,A-A’通電，則電機產生逆時針方向的自旋運動；相反，若順序循環按照相序D-D’,C-C’,B-B’,A-A’通電，電機產生順時針自旋運動。

1.3 傾斜運動原理

磁阻型球形電機定轉子結構關于俯仰運動與偏航運動高度對稱，因此，可以通過分析轉子單對齒以及縱剖面下的3組線圈的通電作用，了解電機傾斜運動原理。與自旋運動不同，在完成傾斜運動時，轉子只有兩極，因此，定子相間的緯度角越大，電機對完成傾斜運動時的啟動轉矩的要求越高。本文設計的定子相間緯度角為33°，既符合電機完成傾斜運動的結構需求，又可以為轉子線圈留下足夠的工程余量。

圖3(a)為0°經度角時的剖面圖，轉子齒與定子F-F’相對齊(中心線重合)，此時磁通主要在F-4-4’-F’軸線上流動。同樣，若此時給F-F’相通電，轉子僅受徑向磁拉力可以達到“自鎖”的狀態。僅通電G-G’相，轉子受到切向磁拉力順時針偏轉。此種通電方法的步進角αstep與定子相經度角相同為33°。為減小步距角，可以使用兩對線圈的通電方法，具體的開環通電相序如下：如圖3(a)定轉子磁極對齊為起始位置，同時通電F-F’,G-G’兩相，在轉子4-4’偏轉經度角略小于16.5°時，接著斷開F-F’相，轉子繼續順時針偏轉。這種方法減少了一半的步距角，但也相應減少了電機關于傾斜運動的輸出轉矩。

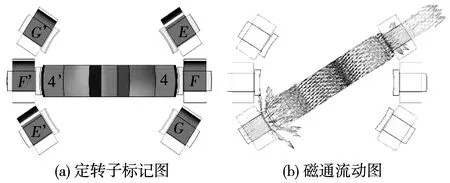
圖3 傾斜運動示意圖

從理論上可以通過多對線圈的通電方法，完成電機的傾斜運動，但多對線圈與轉子間的電磁場計算更為復雜，考慮到通電線圈的激勵磁場之間存在相互影響，限于硬件設備條件有限，本文暫不分析多種通電方法下的傾斜運動。

2 磁阻型球形電機建模

2.1 數學模型

目前，關于球形電機常用的轉矩建模的方法有洛倫茲力法、虛位移法以及麥克斯韋張量法[14-16]。由上文可知本文提出的磁阻型球形電機的工作原理與永磁式球形電機完全不同，參考文獻[17]，類似于開關磁阻電機的線性建模，基于能量法對球形電機進行數學建模。忽略通電線圈間的磁場影響，建立磁阻型球形電機最小模型，圖4為單線圈和轉子組合模型。

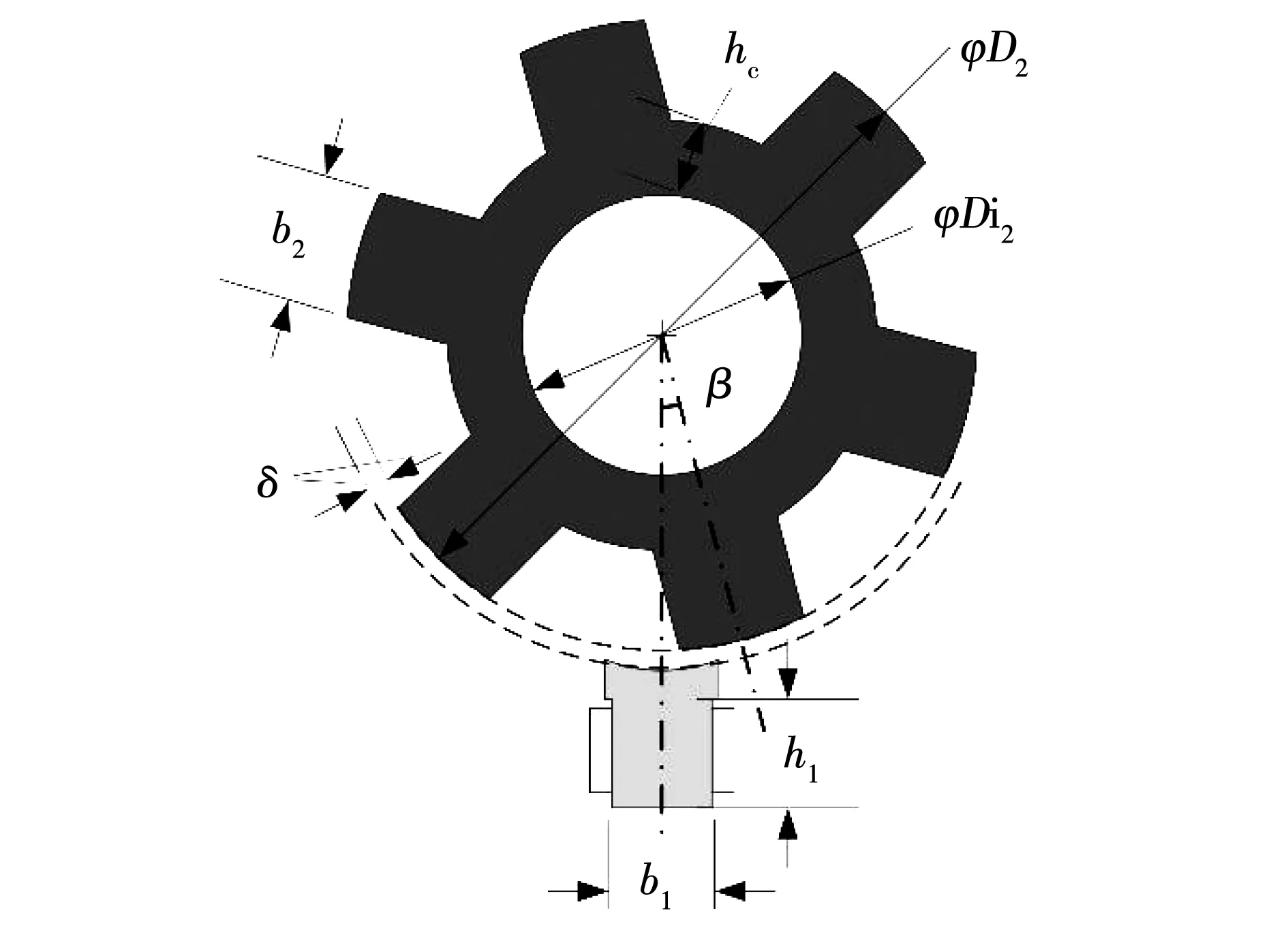
圖4 單線圈最小模型示意圖

與傳統旋轉電機不同，球形電機不僅在空間運動方面增加了2個自由度，而且轉子位置與姿態也會影響電機的動靜態性能。為了便于分析和描述球形電機的運動特性，如圖5建立定轉子坐標系，定子固定坐標系為XYZ直角坐標系，轉子動坐標系為αβγ旋轉坐標系，其中β角為轉子繞Ζ軸逆時針旋轉角度，α角為轉子從XOY平面逆時針旋轉角度，γ角為轉子逆時針自旋角度。

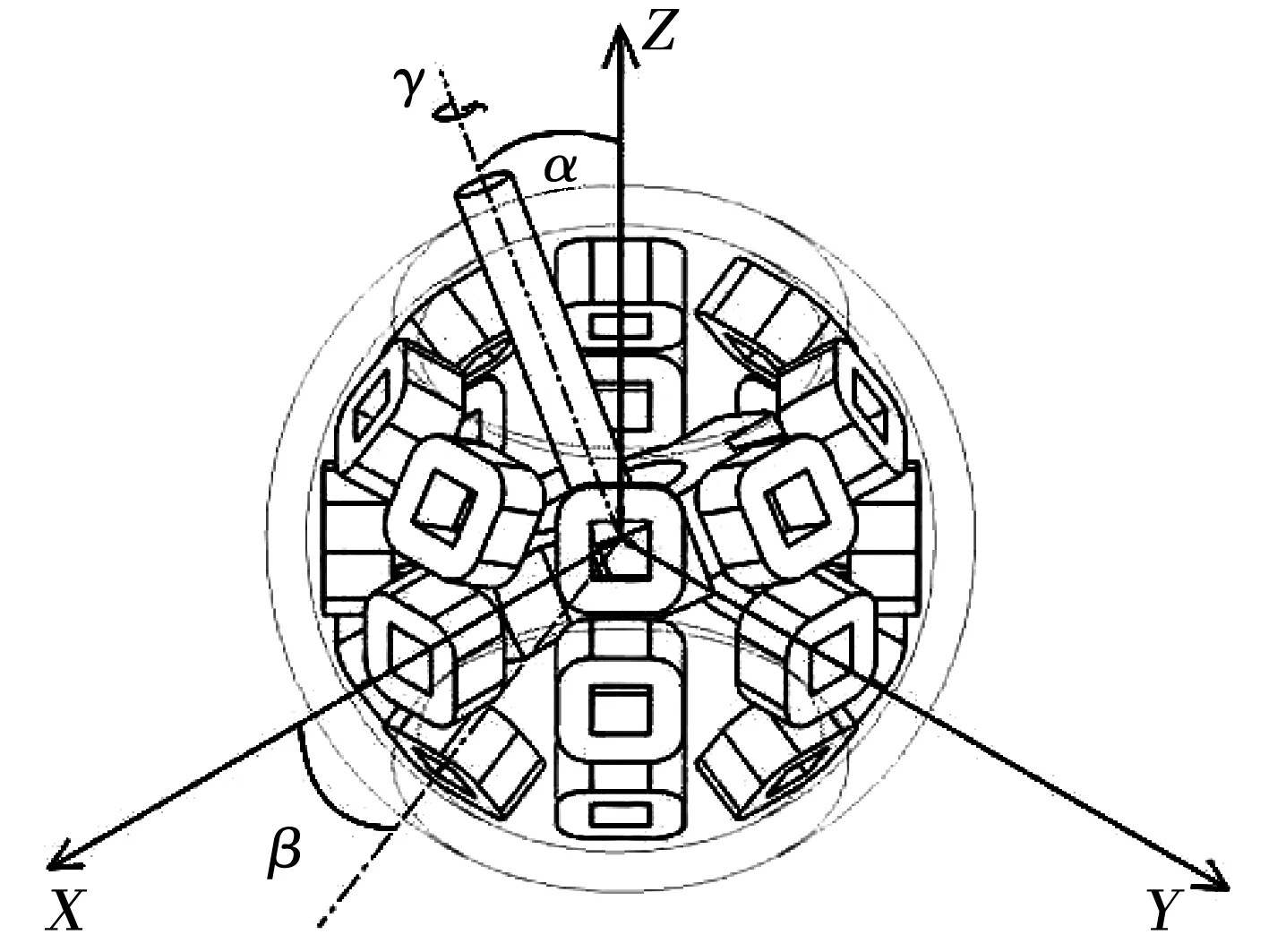
圖5 定轉子坐標系

在基本數學建模之前，假設模型滿足以下條件：

1)忽略集膚效應和邊緣效應；

2)忽略漏磁通；

3)忽略定子鐵心與定子磁軛處磁飽和；

4)定轉子徑向與軸向的相對氣隙均勻；

5)轉子繞三軸旋轉規定逆時針方向為正；

6)定子鐵心和轉子體磁導率無窮大。

本文提出的電機模型共有24個通電線圈，取單線圈進行分析，電壓方程為

(2)

忽略定子繞組上的電阻Rk的情況下，式(2)可以變化為

(3)

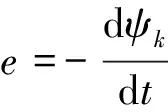
在球形電機中，ψk為關于繞組電流和轉子位置角的函數，表達式為

ψk=ψk(i1,i2,i3,…i24,β,α)。

(4)

單個通電線圈導通時，忽略相間電感，磁鏈方程可以表示為

ψk=Lk(ik,β,α)ik。

(5)

其中α為轉子傾斜位置角，即傾斜方向下轉子中心線與定子相中心線夾角。

根據文獻[15]，球形電機采用笛卡爾方法建立的多剛體動力學方程組為：

(6)

(7)

(8)

(9)

(10)

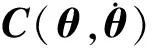
磁阻型球形電機轉子體關于x、y方向結構對稱，轉動慣量一致，在z方向的轉動慣量則偏大，具體數值如表1所示。

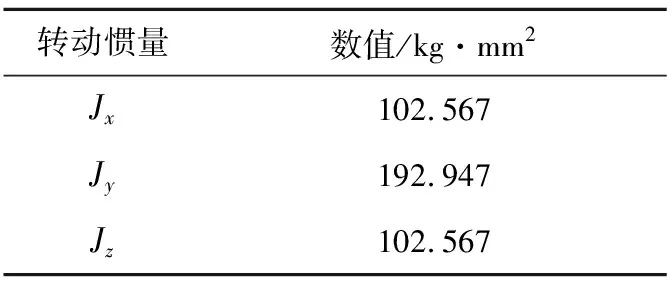
表1 球形電機轉子體轉動慣量J

基于能量法推導磁阻型球形電機的機電聯系方程為

dWe=dWm+dWmec。

(11)

其中：

(12)

式中:dWe為dt時間內輸入電機中的凈電能；dWm為dt時間內磁場吸收的總能量；dWmec表示為dt時間內機械能的增加量；在式(12)中的磁場儲能Wm和磁鏈ψ都為線圈電流i和位移x的函數；將式(12)代入式(11)中，可以得到

(13)

由于di和dx相互獨立，因此滿足(13)式時di和dx系數皆為0，所以

(14)

在旋轉電機中，位移?x可以表示為?x=r?θ，將其代入式(14)可得

(15)

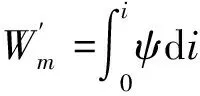
根據本節假設條件1)和3)，球形電機的電感模型為線性化模型，轉矩可以根據電感關于角位移的微分求得：

(16)

在安匝數一定的情況下，電感L的取值可以通過等效磁阻求解，即

(17)

式中:N為線圈匝數；R為氣隙磁阻；μ0為真空磁導率；Ag為等效氣隙截面積；δ為氣隙長度。

2.2 電機有限元建模

由于電機的電感模型在三維場域的高度非線性，電機的動靜態求解和磁場分析十分復雜，基于建立的電機數學模型，本文采用有限元法完成數值求解。Maxwell軟件中，分析三維電磁場域時有限元分析的剖分單元為三維單元，軟件使用的單元為四面體。文獻[18]在軟件中對磁阻型球形電機進行建模，手動剖分電機模型，得到207 822個最小網格，由圖6可以看出電機的剖分足夠精密，仿真得出的結果將更加精確。

圖6 電機剖分圖

本文基于Maxwell 3D的靜磁場仿真計算是在一對線圈通電的條件下進行分析，以數值解的形式驗證上述基本數學模型，并通過曲線擬合的方法表征電機的矩角特性和電感曲線，對電機的動靜態性能起著重要作用。Maxwell軟件提供虛位移法和洛倫茲力法對3D模型進行磁場分析，本文基于虛位移法對電機進行電磁仿真。磁阻型電機有限元建模參數如表2所示。

表2 球形電機結構參數

取球形電機中2種基本運動—自旋運動和傾斜運動進行靜磁場計算，仿真結果如圖7所示。

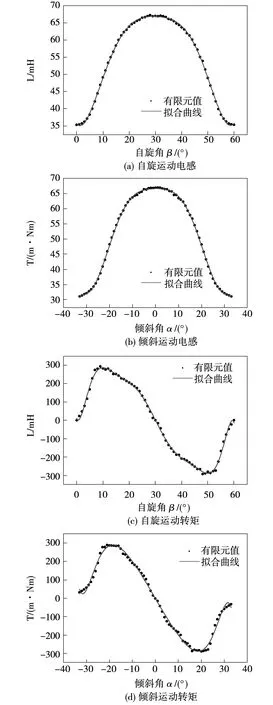
圖7 電感、轉矩—位置角特性曲線

其中(a)和(b)圖分別表示2種運動情況下的相電感曲線，(c)和(d)圖分別表示自旋轉矩和傾斜轉矩。從圖(a)和圖(b)可知相電感曲線關于定轉子對齊位置對稱分布，由于極靴的存在，電感線性變化區域較寬。從圖(c)和圖(d)可知，自旋運動下的有效轉矩區域為β=5°～25°，傾斜運動下的有效轉矩區域為α=5°～25°。分析靜態下的相電感曲線和矩角特性可以更加清楚的了解球形運動的原理，并為電機開環和閉環運行做好理論基礎。

3 電機模型結構設計

在電機設計的過程中，考慮到電機參數對電機性能的影響，限于篇幅，本文取5個主要參數進行仿真分析。針對球形電機中2種典型運動—自旋運動與傾斜運動，以電機的輸出轉矩、氣隙磁密和定子磁軛的磁密大小為目標，分析不同參數的影響效果。轉子初始位置如圖3(a)和圖4所示，計算長度為單對通電線圈條件下一個步進角。

3.1 定子形狀

設計電機之初，提出了2種形狀的定子外殼，圖1(a)和圖1(b)分別表明了球殼型定子與骨架型定子的結構。分析不同形狀的定子結構對磁場的影響，可以得出在電磁線圈通電的情況下，磁通的流動方向因為定子磁軛結構的不同而不同。在磁路中，磁通總是尋找最小磁阻的位置進行流通，因此在傾斜運動時，球殼型的定子結構中磁通流動更加均勻理想，電機的效率將更高。

經過有限元計算，由圖8可以得出，無論是自旋運動還是傾斜運動，就電磁轉矩大小而言，球殼型電機的優勢更大。氣隙磁密與定子磁軛的磁密影響如圖9所示，圖9(a)～圖9(c)圖分別表示骨架型電機的氣隙磁密與自旋、傾斜運動狀態下的軛部磁密，圖9(d)～圖9(f)則表示球殼型電機。對比分析，骨架型結構鐵心磁密高過1.8 T,更容易工作在磁飽和狀態。多重比較，最終選擇球殼型結構。

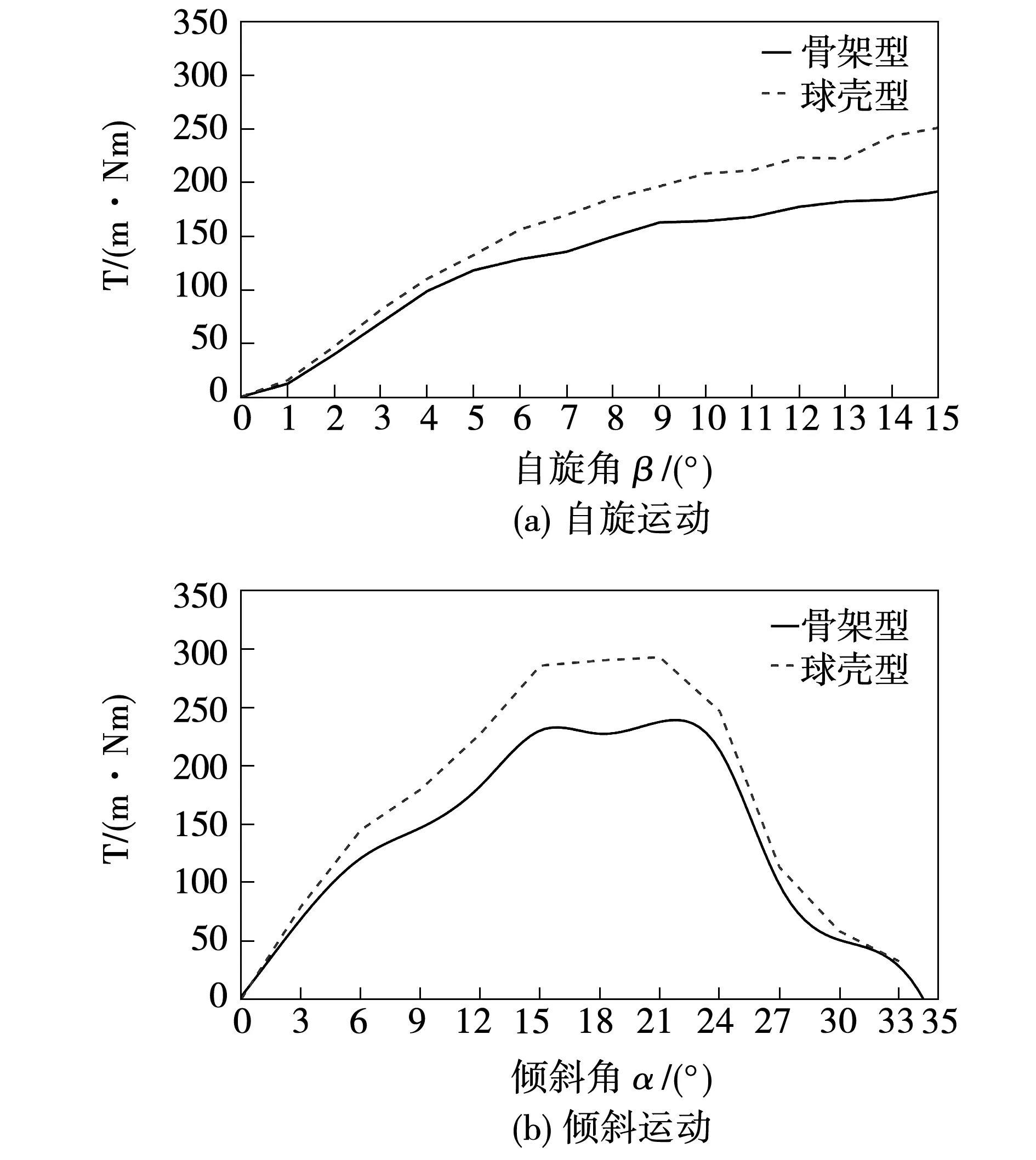
圖8 單步進角矩角特性曲線

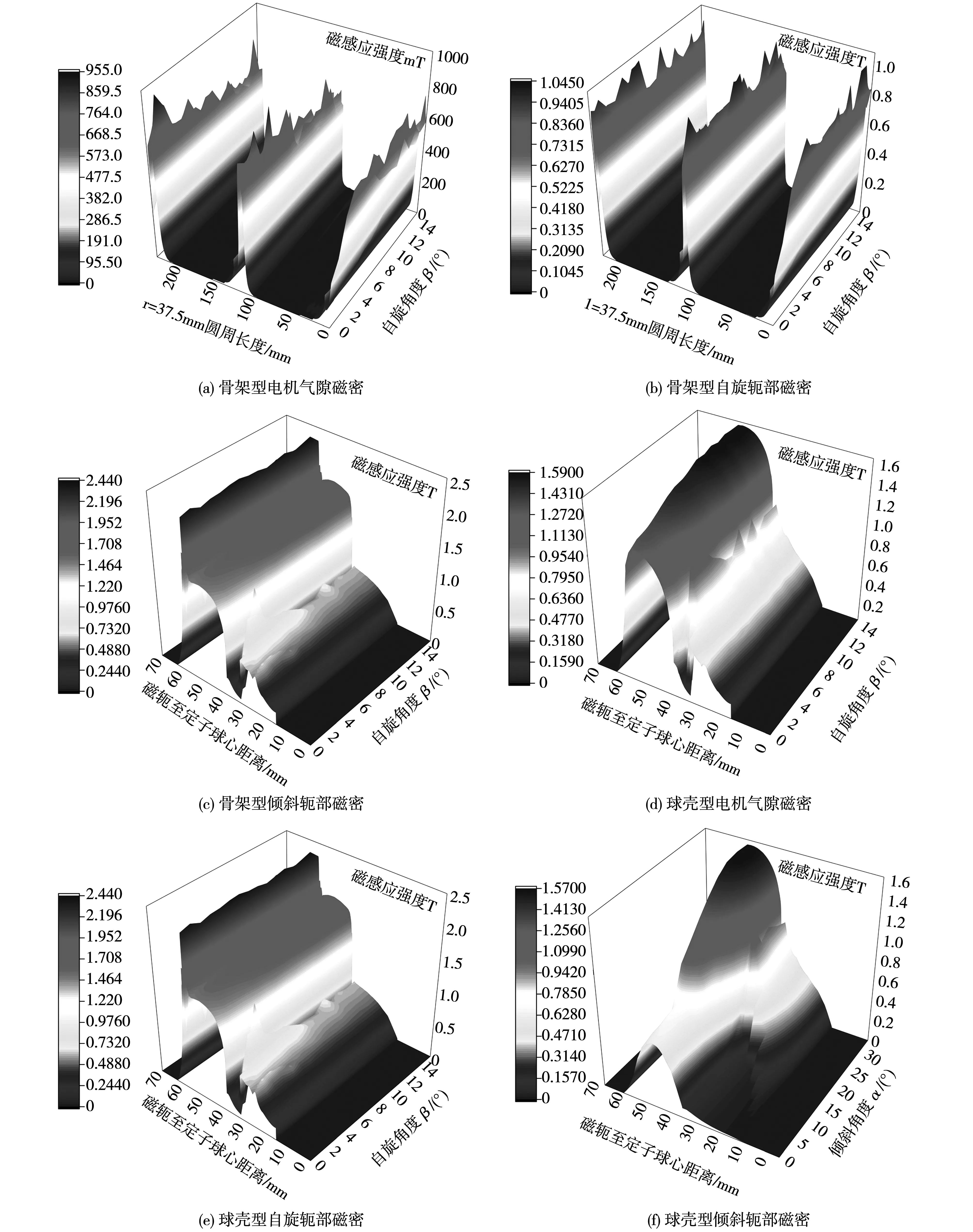
圖9 氣隙磁密與磁軛磁密分布圖

3.2 極靴尺寸

在電機定子鐵心末端添加極靴可以增大定轉子極相對接觸的面積，增大有效轉矩的作用范圍。取0.5～2.5 mm的極靴高度hj進行計算，如圖10，極靴的高度對輸出轉矩的幅值影響不大。對氣隙磁密、定子軛部磁密的影響也在5%以內。因此在電機本體設計中，另外考慮到防止線圈滑落的作用和方便電機加工，如表2所示選擇2 mm高度的極靴進行設計。

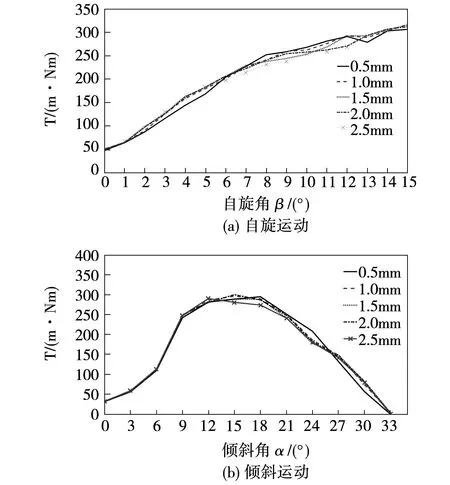
圖10 單步進角矩角特性曲線

3.3 線圈安匝數

由文獻[14-16、19]可以得出，在開環通電一對線圈且安匝數為2 400 A的情況下，永磁球形電機的輸出轉矩在150～250 m·Nm范圍。相比較而言，觀察圖12可知，在新型磁阻型球形電機上使用700 A的安匝數，在減少近一倍安匝數的情況下，電機的輸出轉矩依然可以達到250 m·Nm，相比較同等尺寸的永磁球形電機，至少提高了74%的電磁轉矩。

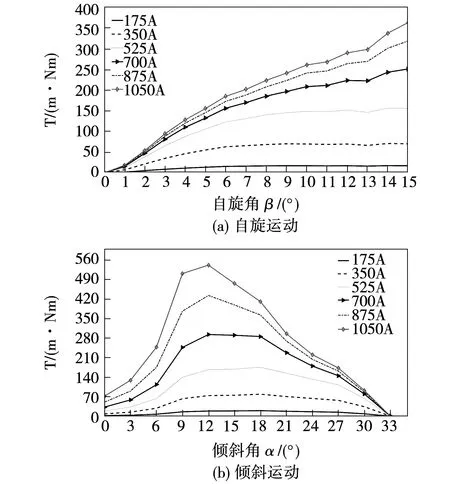
圖12 單步進角矩角特性曲線

圖13表明安匝數在0～850 A范圍內電機鐵心工作在未飽和區域，通電線圈超過850 A安匝數，應考慮鐵心飽和對電機性能的影響及電機效率的下降。

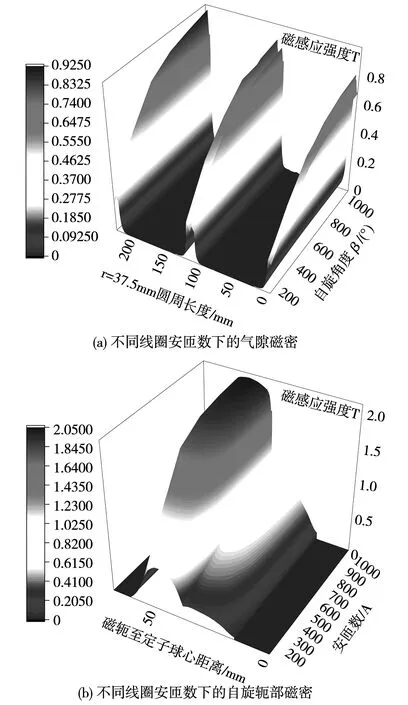
圖13 氣隙磁密與磁軛磁密分布圖

3.4 氣隙長度

球形電機的有效電磁轉矩直接受氣隙磁密徑向分量的基波幅值影響[20]。假設磁通全部在徑向上通過氣隙，定子極靴與轉子之間的氣隙將直接影響電機電磁轉矩的大小。隨著氣隙長度δ的增大，磁路磁勢消耗增大，輸出轉矩減小。

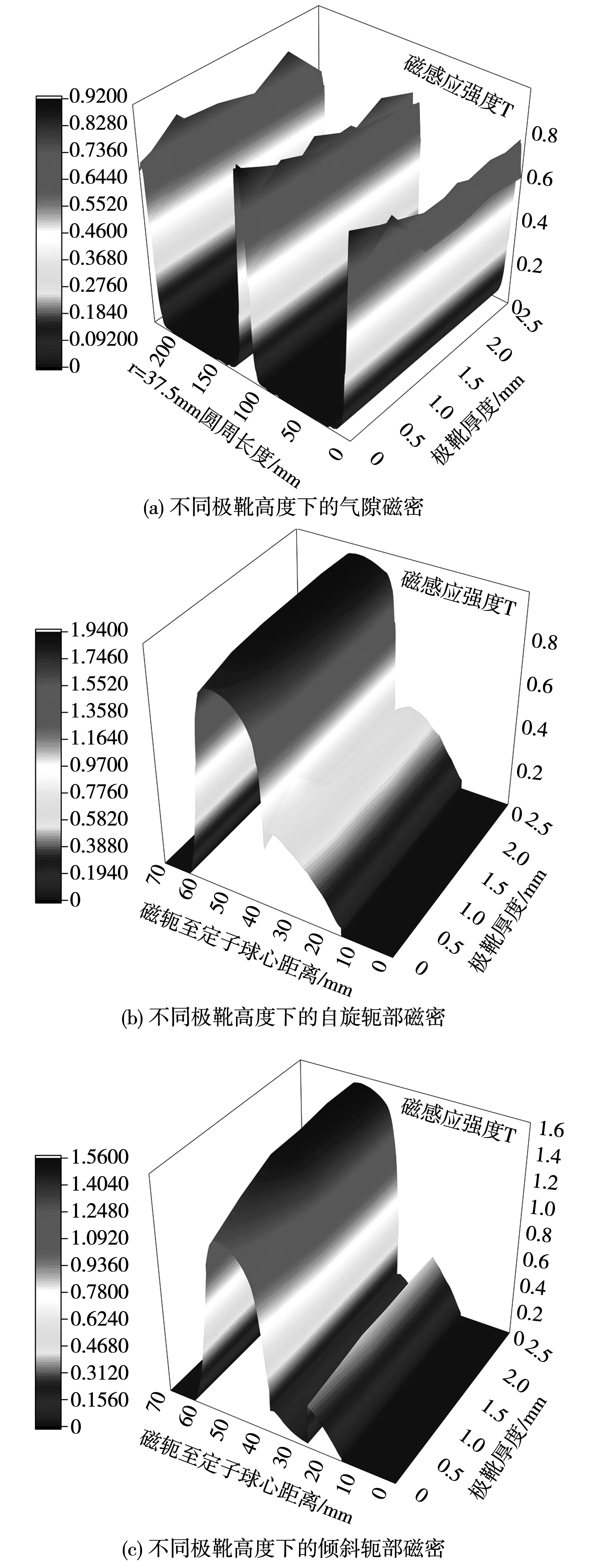
圖11 氣隙磁密與磁軛磁密分布圖

取氣隙長度δ范圍為0.5～2 mm的電機模型進行分析計算，其對2種典型運動的輸出轉矩影響如圖14所示。由于極靴的存在，氣隙長度對轉矩的影響集中在β=0～7°，α=6～24°的范圍內，在δ=0.5 mm時，轉矩波動比較明顯。由圖15可知，氣隙長度對氣隙磁密的影響比較明顯，式(17)表明氣隙長度在恒定安匝數條件下與電感成反比，即與磁鏈、磁密成反比，而自旋與傾斜狀態下的磁軛密度分布趨勢大致相同。

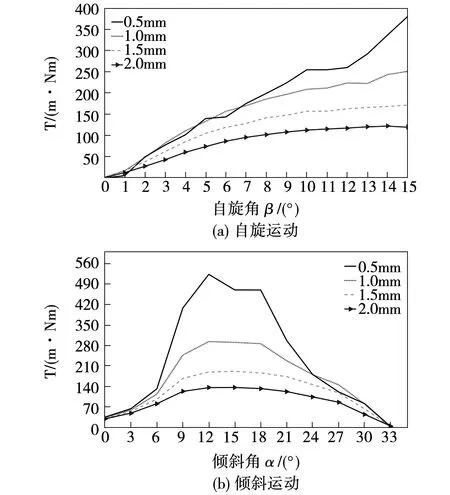
圖14 單步進角矩角特性曲線

圖15 氣隙磁密與磁軛磁密分布圖

3.5 定轉子尺寸

為簡化電磁場分析，電機的定子磁極結構設計關于XOY面與XOZ面均勻對稱。取定子磁極寬度b1(長度l1)范圍8～10 mm進行計算，在自旋運動的換向位置角附近和傾斜運動初始位置處，定子磁極寬度對輸出轉矩的影響很小，如圖16所示，這是因為磁阻型球形電機極靴的存在，增大了定轉子相對接觸面積，而在轉子運動一定角度后，空間位置的改變使得定子磁極寬度對輸出轉矩的影響更為明顯。圖17是轉子磁極寬度b2對電機轉矩的影響曲線。隨著轉子寬度的增大，自旋運動的輸出轉矩得到提高，傾斜運動的啟動轉矩也有所提升。另一方面，需要考慮的是，轉子的轉動慣量也會增加，相應減弱了電機的負載能力。

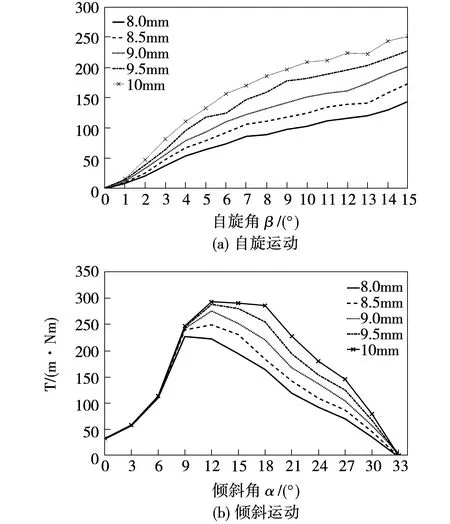
圖16 單步進角矩角特性曲線

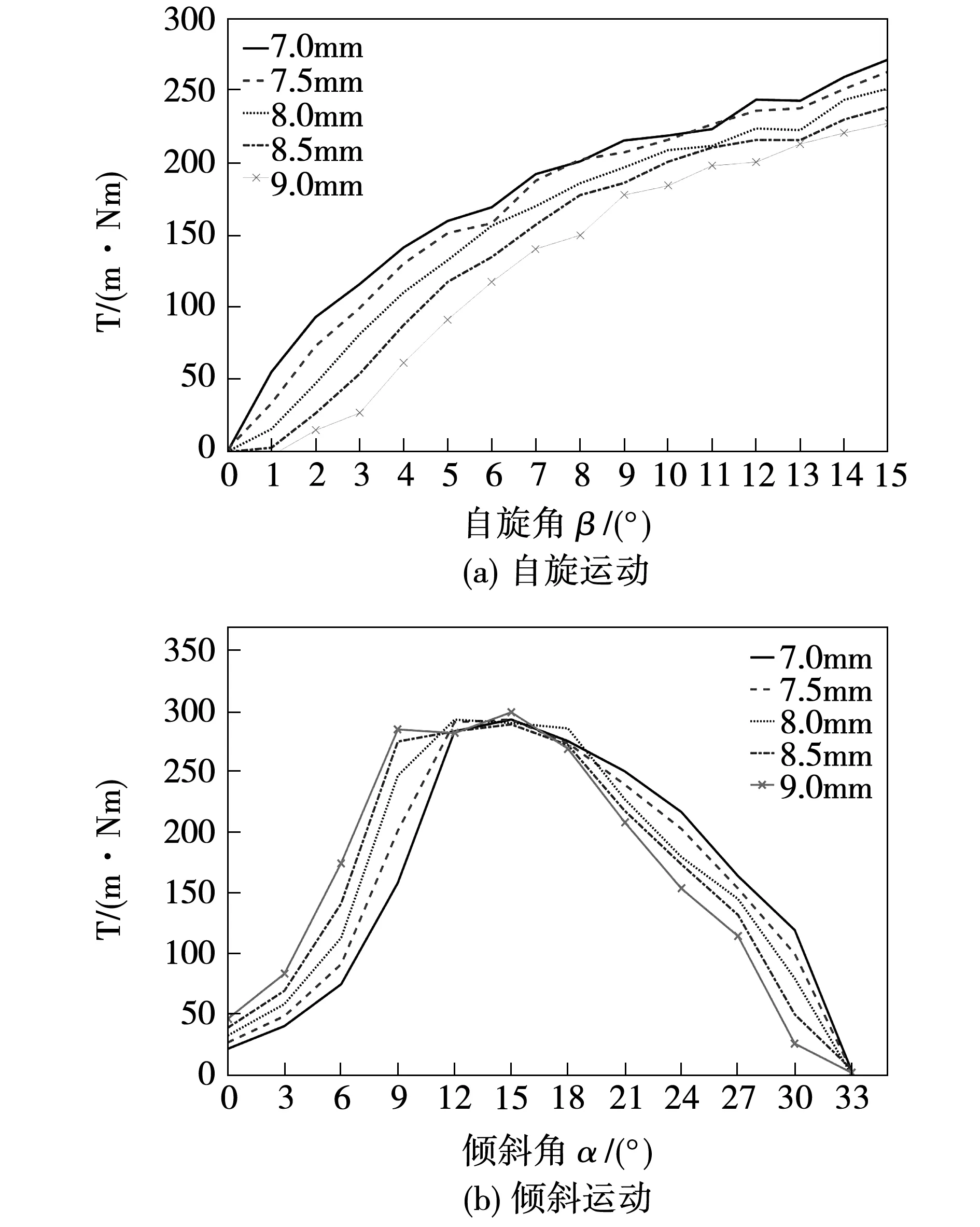
圖17 單步進角矩角特性曲線

圖18表明定子鐵心長度對氣隙磁密的影響近似線性，從磁路的角度分析這是由于鐵磁材料的空間占用率變高，磁勢消耗減小所致。定子鐵心長度和轉子磁極寬度對磁軛磁密的影響較小，在電機設計的過程中優先級較低。

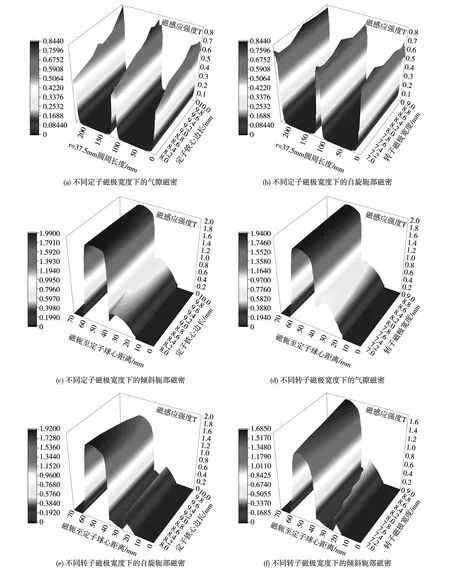
圖18 氣隙磁密與磁軛磁密分布圖

表3給出了本節電機結構設計使用的主要參數及其仿真范圍。

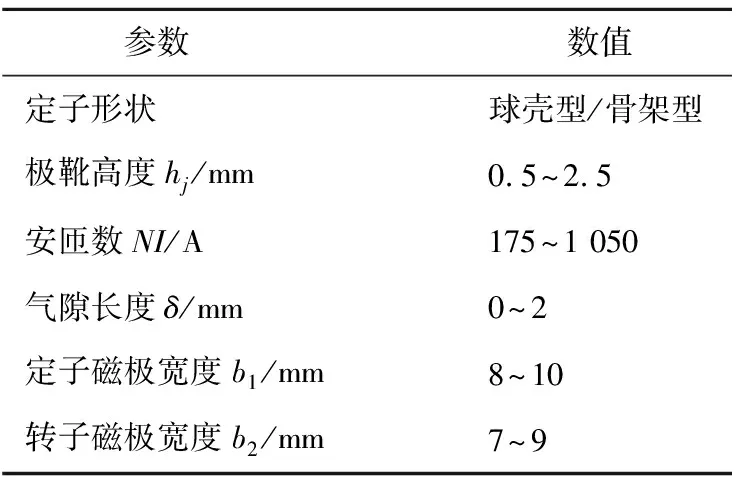
表3 主要參數仿真范圍

4 結 論

本文提出了一種新型磁阻型球形電機，在有限元法的基礎上對其進行結構設計與磁場分析。相比較永磁球形電機，新型結構的轉子簡化了電機結構，提高了電機的輸出轉矩，降低了通電策略的難度。通過分析電機參數對輸出轉矩、氣隙磁密和定子軛部磁密的影響，確定主要參數的優化范圍。本文設計電機的方法為相似結構的球形電機設計提供了參考，得出的結論為下一步電機的參數優化提供了依據。