考慮荷載修正的襯砌背后空洞對結構安全性影響分析*

肖南潤 丁祖德 劉正初 任志華

(1.昆明理工大學建筑工程學院 昆明 650500； 2.中鐵二院昆明勘察設計研究院有限責任公司 昆明 650200； 3.云南省公路科學技術研究院 昆明 650513)

0 引言

隨著我國西部大開發的進一步推進，大量基礎設施建設進入了快速發展階段。在隧道建設快速發展的同時，由于西部地質條件復雜，且受限于施工及監測技術水平，引發隧道缺陷，影響隧道的安全運營[1-2]。其中，襯砌背后空洞是我國山嶺隧道最為常見的質量缺陷之一[3-4]。空洞會直接影響襯砌結構的受力狀態，從而影響其承載力和安全性[5]。

國內外學者分別采用理論分析、數值計算和模型試驗等方法進行了相關研究[6-13]。應國剛等[6]提出了一種荷載-結構模型的修正計算方法，確定了空洞臨近范圍內的圍巖壓力。MEGUID M A等[7]通過數值模擬，分析了襯砌背后空洞對圍巖壓力的影響，認為圍巖壓力在空洞臨近范圍隨空洞尺寸的增大而增大。謝鋒等[8]采用地層-結構法探討了襯砌背后空洞存在時圍巖壓力的分布規律，并對荷載結構計算模型進行修正。在模型試驗方面，方勇等[9]和佘健等[10]通過室內模型試驗，對不同圍巖、不同空洞位置以及不同地應力場條件下，襯砌的破壞形式、受力分布規律及承載力大小進行了研究。也有學者通過數值計算與模型試驗相結合的方法，從空洞位置、空洞類型等方面，對襯砌結構承載力及安全性展開研究[11-13]。

現有研究加深了襯砌背后空洞對襯砌及圍巖受力影響的認識，但考慮圍巖壓力修正，開展不同空洞位置與空洞范圍下，襯砌安全性變化的研究較少。鑒于此，本文改進了空洞存在時的荷載修正計算方法，建立不同空洞位置、不同空洞范圍條件下的襯砌結構內力計算模型，分析襯砌的內力分布特征及安全系數變化規律，為既有隧道襯砌結構安全性評價提供依據。

1 計算模型

1.1 工程背景

以云南省某公路隧道為背景，開展襯砌背后空洞對結構安全性影響的研究。隧道開挖斷面寬12.24 m，高9.57 m。襯砌斷面如圖1所示。二次襯砌采用C30素混凝土襯砌，厚40 cm。隧道按深埋考慮，圍巖級別為Ⅳ級，相關計算參數參照《公路隧道設計細則》[14]選取，具體見表1。

表1 計算模型材料參數

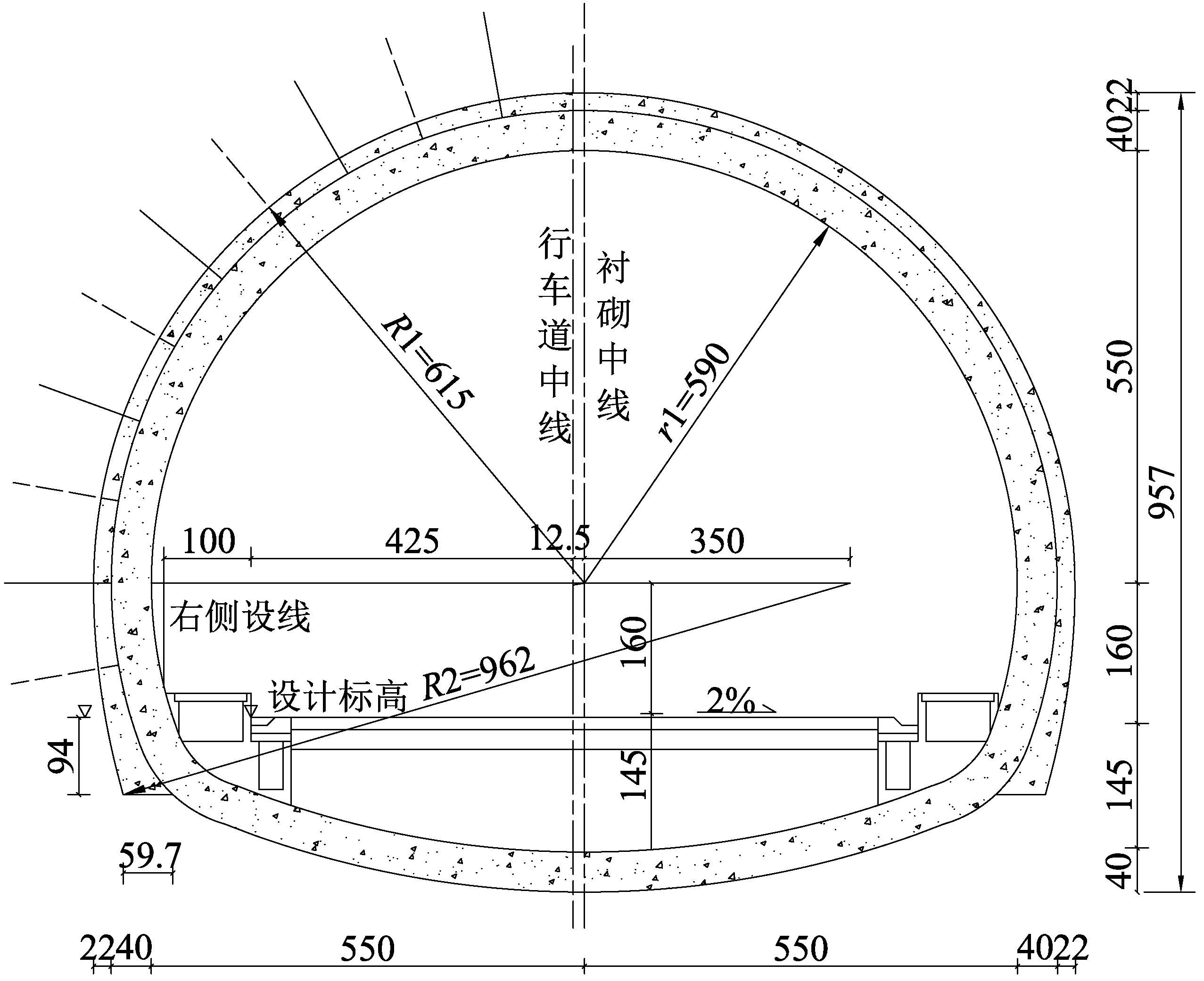
圖1 隧道斷面圖(單位：mm)

1.2 圍巖壓力修正計算方法

依照規范計算得到隧道豎向圍巖壓力q=136.5 kN/m，水平向圍巖壓力e=54.4 kN/m，二次襯砌承載圍巖荷載比例取30%[14]。采用荷載-結構法計算背后空洞對襯砌結構受力性能的影響時，圍巖壓力取值不能簡單地去除空洞區荷載與約束，必須考慮空洞兩側的圍巖壓力集中效應[15]。應國剛等[6]提出了基于三角面積等效的圍巖壓力修正計算方法，但采用三角形面積等效，襯砌背后空洞較大時應力集中效應偏大，鑒于此，本文采用梯形面積等效方法，以改進圍巖壓力計算方法，如圖2所示。

圖中，r為空洞半徑；q為無空洞時隧道上覆荷載；θ為空洞存在對圍巖壓力的影響范圍與空洞半徑之比；λ為圍巖壓力增大段與圍巖壓力影區域比例；qmax為壓力峰值；B0表示最大開挖寬度的一半。

空洞影響范圍一般為3r[6]，最大影響范圍為B0，根據空洞半徑大小，有以下3種情況：

當r≤B0/4時，空洞區域荷載由空洞兩側襯砌承擔。因此，圖中兩陰影面積相等：

S1=S2

(1)

(2)

S2=qr

(3)

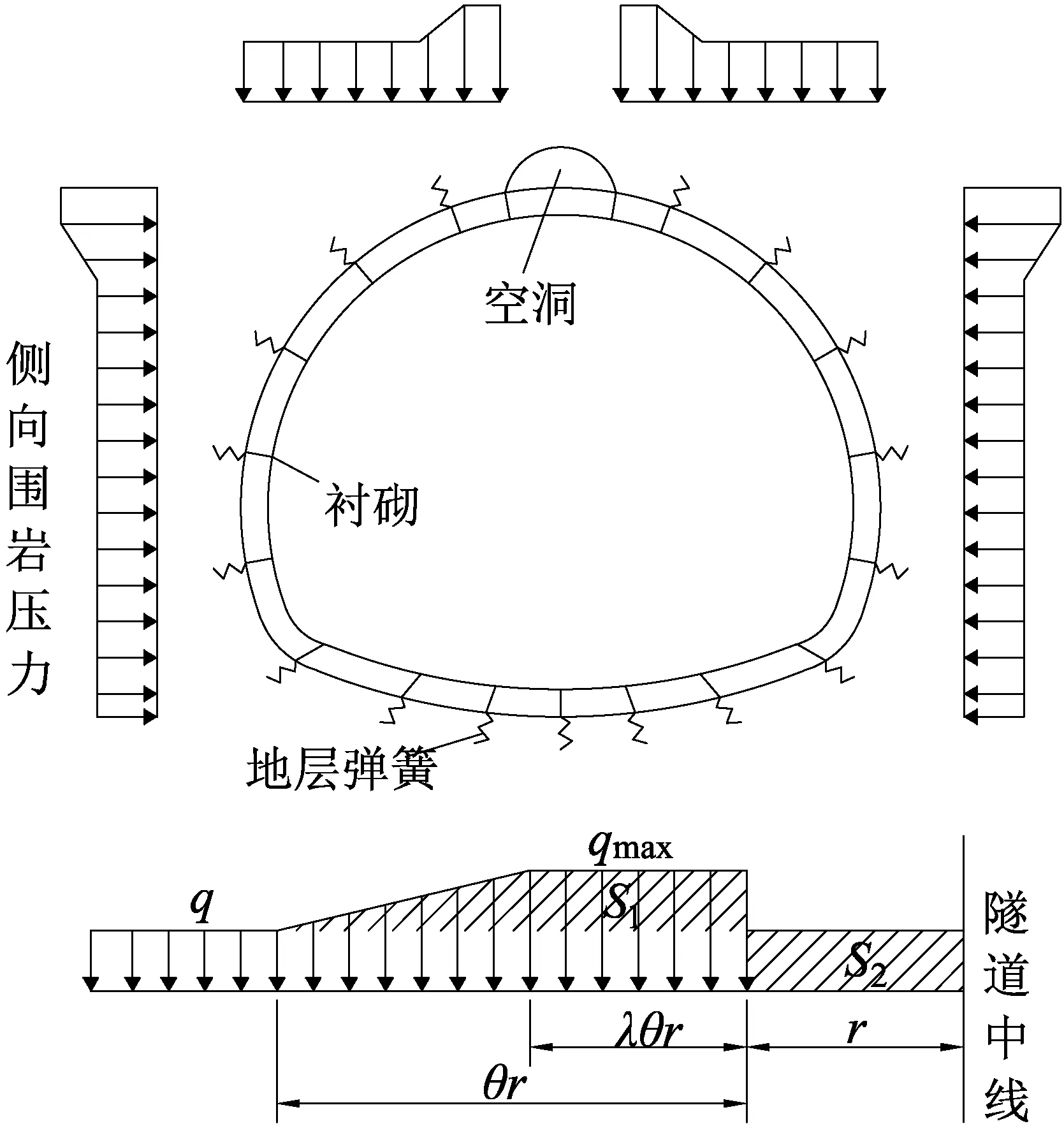
圖2 空洞存在時的修正荷載-結構計算模型

當r>B0/4時，空洞影響范圍到最大開挖寬度處，同理可知:

(4)

根據相關模型試驗[6]，空洞影響范圍一般為3r，峰值靠近空洞邊緣側，位置約為1/3影響范圍內，故θ和λ的取值分別為3和1/3。當r≥B0/2后，空洞影響區域變為矩形，綜上可得qmax為：

(5)

確定隧道最大開挖寬度及空洞半徑后，結合圖2及式(5)，計算可得空洞存在時的修正圍巖壓力。

1.3 計算工況

本次計算主要考慮空洞位置和空洞范圍的影響，其中空洞位置取為拱頂空洞和左側拱腰空洞，空洞范圍α取15°至60°。圖3為空洞缺陷示意，計算工況見表2。

(a) 拱頂空洞

(b) 單側拱腰空洞

表2 計算工況

1.4 襯砌安全性評價方法

襯砌截面安全系數K為襯砌極限承載力與其所受軸力之比[14]。根據襯砌所受偏心距不同，可分為兩種情況：

(1)當偏心距e0≤0.2 h時，安全系數按抗壓強度進行計算：

(6)

式中，Ra為混凝土的抗壓極限強度；K為安全系數；N為軸力，kN；b為截面寬度，m；h為截面厚度，m；φ為構件縱向彎曲系數；α為軸向力的偏心影響系數。

(2)當偏心距e0>0.2 h時，由截面抗拉強度控制其承載能力，安全系數計算公式為：

(7)

式中，Rl為混凝土的抗拉極限強度；其他符號含義同前。

2 計算結果分析

2.1 軸力分析

以襯砌空洞范圍α=30°為例，計算得到襯砌的軸力分布云圖如圖4所示。襯砌軸力隨著空洞范圍變化的分布曲線見圖5，軸力以受壓為負。

(a)完好襯砌

(b)拱頂空洞

(c)左側拱腰空洞

由圖4可知，空洞出現位置不同，軸力分布形態基本一致，但空洞的出現引起襯砌軸力重分布，各典型部位軸力值差異明顯。結合圖5分析可知,隨著空洞范圍增大，空洞發生處，襯砌軸力明顯降低，其余部位軸力變化較小。拱頂空洞角度從0°增大到60°時，拱頂軸力從-221 kN變化到-128.7 kN，減小了41.8%。當單側拱腰存在空洞，空洞范圍從0°增大到60°時，拱腰軸力從-281.6 kN變化到-242.9 kN，減小了13.7%。拱頂空洞對襯砌軸力的影響明顯大于單側拱腰空洞。

(a)拱頂空洞

(b)左側拱腰空洞

2.2 彎矩分析

以襯砌空洞范圍α=30°為例，計算得到襯砌的彎矩分布云圖如圖6所示，彎矩以結構內側受拉為正。由圖6可知，拱頂存在空洞時，拱頂處的彎矩方向發生反轉，表現為拱頂外側受拉，其余典型部位彎矩變化較小。當拱腰存在空洞時，彎矩最大值出現在空洞部位，表現為外側受拉破壞。

(a)完好襯砌

(b)拱頂空洞

(c)左側拱腰空洞

由圖7可知，拱頂空洞時，隨空洞范圍的增大，彎矩圖呈現“花瓣狀”，具體表現為拱頂及臨近部位彎矩方向發生反轉，彎矩幅值先減小后增大。當拱頂空洞角度從0°增大到60°時，拱頂彎矩從37.14 kN·m變化到-45.79 kN·m，彎矩幅值增長了約23%。單側拱腰出現空洞時，彎矩圖表現為“羊角狀”。隨著拱腰空洞范圍增大，拱腰及臨近部位彎矩有增大趨勢，而其他典型部位未見明顯變化。當拱腰空洞角度從0°增至60°時，拱腰彎矩從-29.42 kN·m變化到-132 kN·m，彎矩幅值增大了3.49倍，拱頂及邊墻部位彎矩則分別增大了55.49 kN·m和51.25 kN·m。總體而言，空洞存在的部位，其彎矩分布形態發生改變，且隨著空洞范圍的增大，襯砌受力條件惡化。

2.3 安全性分析

為反應襯砌安全性，計算襯砌各部位安全系數，將其最小值定義為襯砌最小安全系數。襯砌拱頂、單側拱腰背后存在空洞時，采用三次多項式對不同空洞范圍下的襯砌最小安全系數進行擬合，擬合相關系數(R2)分別為0.88和0.99，擬合度較好，結果如圖8所示。圖中采用線圈和箭頭指出最小安全系數所屬部位。

(a)拱頂空洞

(b)左側拱腰空洞

由圖8可知，拱頂存在空洞時，隨著拱頂空洞范圍增大，襯砌最小安全系數出現部位由墻角轉至拱頂，最小安全系數隨空洞范圍增大整體呈下降趨勢。當拱頂空洞范圍在30°以內時，結構最小安全系數出現在墻腳，空洞范圍增至45°及以上時，襯砌最小安全系數則出現在拱頂部位。拱頂空洞60°時，襯砌最小安全系數僅為無空洞時的65%。當單側拱腰存在空洞時，襯砌的最小安全系數均出現在空洞處，拱腰空洞范圍由0°增加至60°，襯砌的最小安全系數減小了80%。

圖8 最小安全系數變化曲線

相同空洞范圍下，相較于拱頂空洞，單側拱腰洞時，襯砌的最小安全系數更低。在空洞范圍均達到60°時，單側拱腰空洞的最小安全系數僅為拱頂空洞的31%。

3 結論

本文以存在空洞缺陷的襯砌為研究對象，建立了考慮空洞影響的圍巖荷載-結構修正計算模型，通過算列研究了拱頂空洞、單側拱腰空洞對襯砌內力和最小安全系數的影響，得出了如下主要結論：

(1)背后存在空洞時，襯砌受力條件惡化，空洞引起襯砌內力重分布，空洞處襯砌彎矩分布形態改變，且彎矩幅值呈增大趨勢。

(2)拱頂或單側拱腰存在空洞時，隨著空洞范圍增加，襯砌最小安全系數降低。

(3)相同空洞范圍下，相較于拱頂空洞，拱腰空洞的安全系數更低。