混凝土箱形截面考慮二階效應的配筋圖算法*

李彬 周東華

(昆明理工大學建筑工程學院 昆明 650500)

0 引言

隨著高強材料的出現使得建筑高度不斷增加，對壓彎構件二階效應分析與計算顯得愈為重要，二階效應會降低結構構件的剛度和承載力，如果在設計階段未考慮二階效應對結構構件的影響，則相當于降低了結構的安全系數。

箱形和工字形截面壓彎構件在結構工程中很常見，如連續剛構橋中的空心薄壁墩、工業廠房中上部設置有牛腿的工字形截面柱。以往對這種工字形或箱形截面配筋是用《混凝土結構設計規范》[1](以下簡稱《規范》)6.2條中工字形正截面承載力計算公式。混凝土構件正截面承載力計算公式的推導，采用等效矩形[2-3]應力圖換算，并規定混凝土受壓區邊緣應變為-3.3‰，也就是無論構件截面內力大小，混凝土受壓區邊緣應變始終為極限應變，這與構件實際受力時的應變狀態不相符，而實際上構件截面上內力大時應變大，內力小時應變小。《規范》中計算壓彎構件配筋時，需要先判斷截面類型是大偏壓還是小偏壓，根據截面類型運用不同的公式計算受壓區高度，再由受壓區高度求配筋面積，計算過程繁瑣。為了避免等效矩形應力換算帶來的誤差，減小計算過程繁瑣，本文嚴格按照混凝土和鋼筋的本構關系，結合《規范》中二階效應計算的增大系數法，經過推導繪制出了二階效應下箱形和工字形截面配筋計算的圖表[4-5]，為箱形和工字形截面壓彎構件配筋計算提供一種簡便的方法[6-7]。

1 計算原理與方法

1.1 本構關系

《規范》中給出的完整的混凝土和鋼筋的本構關系，如圖1。

(a)混凝土 (b)鋼筋

混凝土(a)和鋼筋(b)本構關系的數學表達式：

式中 ，σc、σs為混凝土和鋼筋的應力；εc、εs為混凝土和鋼筋的應變；fc為混凝土抗壓強度設計值；fy為鋼筋抗拉強度設計值；Es為鋼筋的彈性模量。

1.2 混凝土和鋼筋應變區域

《規范》中鋼筋和混凝土的極限應變取值分別為-3.3‰和10‰，據此將混凝土和鋼筋的應變劃分為如圖2的5個區域，每個區域總有一邊上的一點處于極限狀態，這樣就保證了截面上應變組合都處于極限狀態，使得構件破壞時是受壓破壞、受拉破壞或受拉受壓同時破壞。

圖2 截面應變分區圖

混凝土結構受力(包括軸拉、大小偏拉、純彎、大小偏壓、軸壓)時所有的應變狀態，都完全能在圖2中表示出來，這5個區域的截面應變規律和受力情況，如表1所示。

表1 截面應變與實際受力狀態

續表1

上述的5個應變分布區域，適用于各種截面類型的鋼筋混凝土構件，因為①區是軸拉或者偏拉的“受拉”狀態，不考慮其二階效應，所以下文推導的箱形和工字形截面配筋計算方法，是基于②③④⑤區的應變求得的。以矩形截面計算模型，推導公式的最后減去內部小矩形的抗力，即可得到箱形和工字形截面構件的承載力。

1.3 截面承載力

1.3.1 受壓區混凝土合力及位置

圖3 混凝土彈性的應變和應力

(1)

式中，C為混凝土受壓區合力；b、x為混凝土受壓區寬度和高度；αc為混凝土壓應力不均勻系數。

令受壓區合力點對混凝土受壓區邊緣取矩得：

(2)

式中，a為混凝土合力到受壓區上邊緣距離。

可以推出混凝土合力點到受壓區邊緣的距離：

(3)

式中，ka為混凝土受壓合力位置系數。

(2)混凝土邊緣應變-2‰≥εc≥-3.3‰。混凝土處于彈性+塑性階段，混凝土受壓區應力分布為拋物線+矩形，應變及應力分布如圖4。

r=-(2x)/εc

(4)

s=x-r=(1+2/εc)x

(5)

式中，r為混凝土受壓彈性區高度；s為混凝土受壓塑性區高度。

圖4 混凝土塑性階段應變和應力

彈性+塑性階段混凝土受壓區合力：

(6)

αc為混凝土彈性+塑性階段的壓應力不均勻系數，當εc=εcu=-3.3‰時，αc=0.798。令受壓區合力點對混凝土受壓區邊緣取矩得：

(7)

可以推出混凝土合力點到受壓區邊緣的距離：

(8)

1.3.2 受壓區高度系數和內力臂系數

如果知道受拉鋼筋應變，那么再根據已知的混凝土受壓區邊緣應變，就可以確定受壓區高度系數kx和內力臂系數ka，見圖5。

圖5 受壓區高度及內力臂

由圖5的幾何關系可得：

(9)

z=h0-a=(1-kakx)h0=kzh0

(10)

(11)

式中，x、kx為混凝土受壓高度和高度系數；z、kz為截面內力臂和內力臂系數。kx、kz都只與混凝土邊緣應變和受拉鋼筋應變有關。

1.4 截面軸力及彎矩

上文得到了受壓區混凝土的合力及其位置的表達式，不難列出截面的軸力和彎矩的平衡條，下面就分別按兩種情況(中性軸在截面內和在截面外)來計算截面的軸力承載力和彎矩承載力。計算時，考慮為對稱配筋，即有如下關系：

(12)

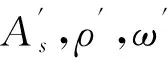
1.4.1中性軸在截面內(區域②③④)

此時，中性軸在截面內，構件受力狀態為大偏拉、純彎、大偏壓，見圖6。

圖6 區域②③④內力圖

由圖6的平衡關系得：

(13)

(14)

式(13)和式(14)兩邊分別同時除以fcbh和fcbh2，得無量綱軸力n和彎矩m：

(15)

(16)

1.4.2中性軸在截面外(區域⑤)

此時，中性軸在截面內，構件受力狀態是小偏壓過渡到軸壓，見圖7。

圖7 區域⑤內力圖

由圖7的平衡關系得：

(17)

(18)

式(17)和(18)兩邊分別同時除以fcbh和fcbh2，得無量綱軸力n和彎矩m：

(19)

(20)

上面推導的為單個矩形截面的軸力和彎矩承載力的計算公式。若要得到箱形和工字形的計算公式，只需從大矩形受壓混凝土的內力中減去小矩形的內力，無須重新推導公式。鋼筋的內力計算則沒有任何變化。混凝土受壓區截面如圖8所示。

圖8 混凝土受壓區截面

綜上所述，在上面推導的公式中截面的彎矩和軸力承載力都是εc和εs的函數，已知了εc和εs，方程中便沒有任何未知量，應力和內力計算變得非常簡單，在圖2的5個應變區域中εc和εs是交替保持在極限應變，另一個可變化，即可按等間隔的賦予不同的值。將圖2中5個區域的應變代入上面的公式進行計算，并將得到的值繪制成圖9中m-n相關曲線族。

圖9 箱形截面一階m-n相關曲線

上圖中包含了軸拉、小大偏拉、純彎、大小偏壓和軸壓等7種受力狀態，可用于配筋計算或截面強度驗算。

1.5 考慮二階效應的m-n相關曲線

當考慮二階效應時，構件或結構的一階彎矩會增大，為簡化計算，可用彎矩增大系數η乘以一階彎矩m1而得到二階彎矩m2，即m2=ηm1，但二階彎矩不得大于截面的彎矩承載力m，即：

m2=ηm1≤m

(21)

上式中的η可按《規范》6.2.4計算：

(22)

式中，e0為初始偏心距，e0=m0/n；m0為荷載彎矩；ea為附加偏心距，ea=max{h/30,20 mm}；l0為構件計算長度。

由于彎矩增大系數中考慮了附加偏心距，一階彎矩中也應包含附加偏心引起的彎矩，即：

m1=m0+ma=n(e0+ea)

(23)

由式(21)和(23)可得到考慮二階效應的設計表達式：

m1=n(e0+ea)≤m/η

(24)

由上式中便可得到：用大于1的η除以彎矩承載力m，便得到了考慮二階效應的m-n的相關曲線，曲線中還包含了參數l0和ω的影響，見圖10。

圖10既可用以配筋計算，也可用以截面承載力復核；配筋計算時，由3個無量綱參數m1、n及λ，便可查得無量綱強度的配筋率ω。另外，考慮了二階效應的圖10中的曲線族均比圖9中壓彎區的沒有考慮二階效應的曲線族縮小了，長細比越大，縮小的程度越大。

(a) λ=30、40、50、60

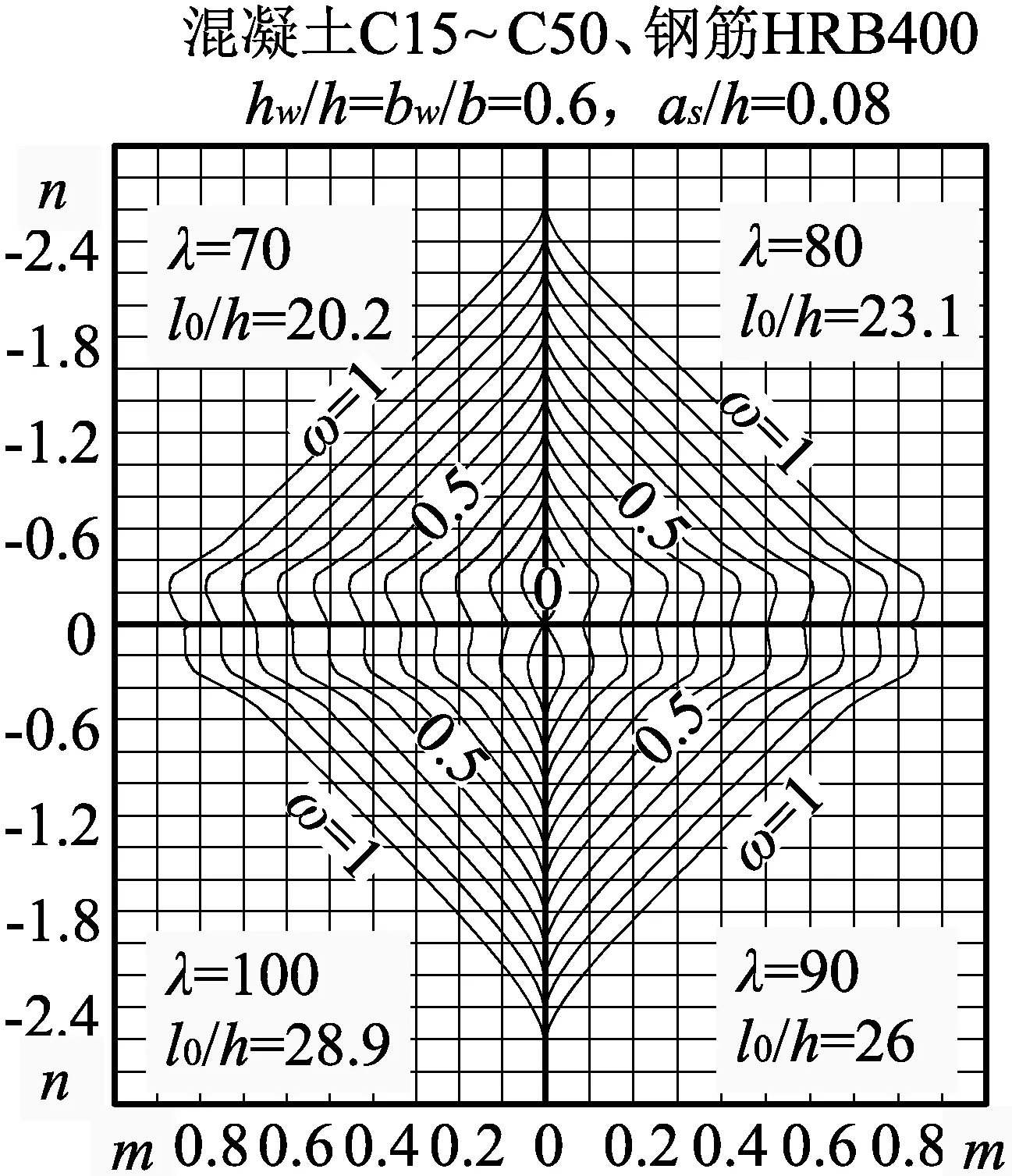
(b) λ=70、80、90、100

2 算例

2.1 規范解法

(1)求附加偏心距：

ea=max{h/30,20 mm}=20 mm

(2)求偏心距增大系數：

h0=h-as=510 mm

l0/h=8 000/550=14.5

(3)計算壓力對受拉鋼筋的偏心距：

ei=η(e0+ea)=209.6 mm

e=ei+h/2-as=444.6 mm

(4)判斷大小偏心：

ei>0.3h0=153 mm

Nb

(5)求相對和受壓區高度：

x=ξ·h0=320.7 mm

(6)計算配筋：

=622 mm2>0.2%A=282 mm2

2.2 本文解法

(1)計算無量綱系數：

(2)計算配筋：

l0/h=14.5，可在圖10(a)第3象限得ω=0.07。

從上面的計算過程可以看到，按《規范》計算相對較為繁瑣，需要計算偏心距增大系數、判斷大小偏心、判斷截面類型等，而本文算法過程則很簡單，無需任何判斷的計算。兩方法的配筋率之比為1 244/1 224=1.016，誤差在3%以內。

3 結論

本文用由應變求應力和內力的新的計算方法，能完整利用《規范》中混凝土和鋼筋的本構關系，構造出5個可能的應變區域，將應變變成了已知量，使得應力和內力的計算變得簡單。

圖9中的諾模圖可用于不需考慮二階效應的配筋計算，而圖10 中的諾模圖則可用于考慮二階效應時的配筋計算。

用本文的諾謨圖計算配筋，快速方便。另外，諾模圖均采用無量綱形式，可一表多用，即可用于C50及以下強度的混凝土和任意大小的截面寬度和高度(b×h)。