電機-減速一體化殼體有限元分析

馬銀生，馮圣國，焦學健，蘇尚彬

（1.255049 山東省 淄博市 山東理工大學 交通與車輛工程學院；2.266071 山東省 青島市 青島天贏智能工業股份有限公司；3.256414 山東省 淄博市 山東工業職業學院 冶金與汽車工程系）

0 引言

隨著社會經濟的快速發展，世界范圍內汽車保有量不斷攀升，對石油的需求也在日益增加，由此引發的環境污染問題愈發嚴重。另外，石油等不可再生資源日益減少。在此背景下，新能源汽車因節能環保等優點獲得迅速發展，純電動汽車成為各國的研究熱點。

純電動汽車減速器是傳動系統的重要部件，減速器殼體對支撐和保護殼體內部齒輪軸系起到重要作用。減速器殼體的強度會直接影響減速器的傳動性能[1]，應有足夠的強度才能保證汽車安全行駛，因此有必要對減速器殼體結構進行強度校核計算。

本文以純電動汽車電機-減速一體化殼體為研究對象，應用有限元法對殼體的強度進行計算，通過力的平衡關系求解各個軸承座承受的載荷大小，建立殼體有限元模型，求解計算后得到殼體的應力及位移分布云圖，并通過查看殼體的最大應力及最大位移來判斷殼體是否滿足強度和剛度要求。

1 殼體強度校核理論

電機-減速一體化殼體采用塑性材料鋁合金，當殼體承受一定程度的載荷后將發生塑性屈服，常用第四強度理論，即畸變能密度理論（Von Mises 理論）作為殼體靜力分析的強度準則。通過該理論可知，若結構上的某一部位的最大應力超過了結構材料的屈服極限，該點就會發生塑性屈服。通過式（1）計算畸變能密度：

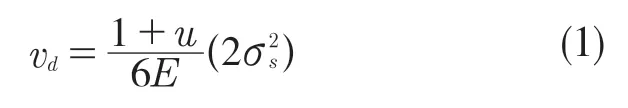
式中：vd——畸變能密度；u——材料的泊松比；E——材料的彈性模量；σs——材料的屈服強度。

通過式（2）對畸變能密度進行計算：

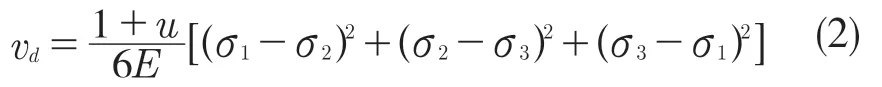
式中：σ1，σ2，σ3——單元的主應力。

由式（1）、式（2）可得屈服準則：

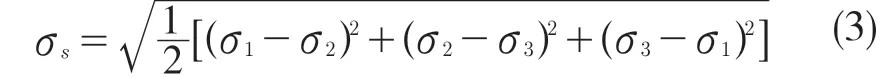
畸變能密度理論的強度應滿足：

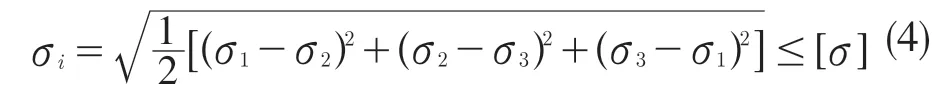
式中：σi——結構上某一點的應力；[σ]——許用應力，可通過式（5）求得：

式中：ns——選取的材料安全系數。

1.3療效標準和評價標準參照《中醫病癥診斷療效標準》,療效標準:有效:治療后癥狀和體征得到有效緩解甚至消失;無效:癥狀和體征無變化,腰痛情況持續存在或12個月內復發持續性疼痛。評價標準:VAS評定疼痛程度:0表示無痛;1-3分表示輕微疼痛,能忍受;4-6分表示疼痛已經困擾患者的生活,睡眠,但尚可忍受;7-10分表示無法忍受的疼痛。

由于電機-減速一體化殼體的結構比較復雜，并且在減速器工作過程中，殼體承受的載荷也比較復雜，因此不能使用傳統的理論力學計算殼體的強度。本文應用有限元法對殼體強度進行計算求解，首先建立殼體有限元模型，然后對模型準確施加載荷及位移約束等邊界條件，最后可通過分析后的應力云圖得到殼體應力分布情況。

2 殼體結構及受力分析

2.1 殼體結構

電機-減速一體化殼體共由2 部分組成：前殼體及后殼體。前殼體與后殼體、后殼體與電機之間均采用螺紋連接，前殼體與后殼體上均設有軸承孔、加強筋及螺紋孔等結構。在前處理軟件HyperMesh 中雖然有三維實體建模功能，但只能創建簡單模型，并不能建立空間結構較復雜的模型。本文使用三維建模軟件CATIA 建立的電機-減速一體化殼體幾何模型如圖1 所示。

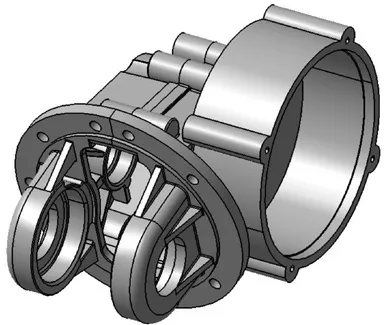
圖1 電機-減速一體化殼體模型Fig.1 Motor-reducer integrated housing model

純電動汽車減速器的傳動原理如圖2 所示。純電動汽車以驅動電機作為動力輸入的來源，電機軸與輸入軸為一體軸，電機帶動一體軸上的齒輪Z1 轉動，齒輪Z1 與中間軸上的齒輪Z2 相嚙合帶動中間軸轉動，然后中間軸上的齒輪Z3 與減速齒輪相嚙合，最終帶動半軸的轉動，驅動汽車能夠正常行駛。

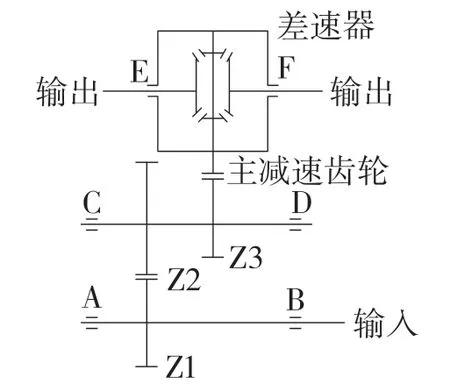
圖2 減速器傳動原理圖Fig.2 Schematic diagram of reducer drive

2.2 受力分析

由于減速器內部的齒輪、軸系及軸承等結構部件的重力對殼體的性能影響很小，所以在分析過程中忽略其重力的影響。

在對殼體進行靜力分析前，需要先計算殼體所承受的載荷。減速器的傳動系采用斜齒輪，斜齒輪在傳動過程中嚙合產生的軸向力Fa、徑向力Fr以及周向力Ft通過齒輪軸傳遞給軸承，進而作用在殼體上，因此先計算各齒輪軸的受力情況，進而計算出殼體所承受的載荷。

斜齒輪間產生的嚙合力可分解成沿齒輪的軸向力Fa、徑向力Fr以及周向力Ft三個相互垂直的分力，各力的計算公式為[2]

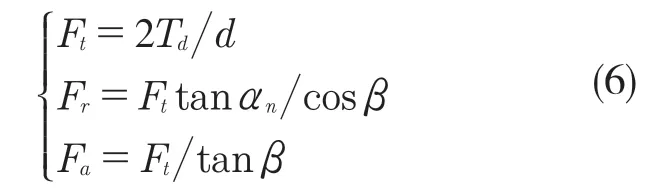
式中：Ft——周向力；Td——齒輪傳遞的扭矩；d——齒輪分度圓直徑；Fr——齒輪徑向力；αn——齒輪法向壓力角；β——齒輪分度圓螺旋角；Fa——齒輪軸向力。

建立峰值轉矩工況下輸入軸的受力分析簡圖如圖3 所示。

軸的兩端支撐點處的受力大小由力學平衡關系式（7）可得：

同樣，根據力學平衡關系式可計算得到中間軸及差速器總成兩端軸承支撐點的載荷大小，最終得到各軸承座所受支反力的大小。各個軸承座所承受的載荷如表1 所示。

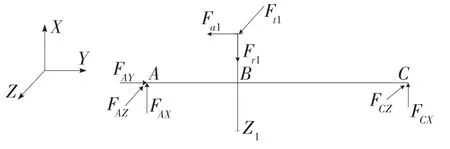
圖3 輸入軸受力分析簡圖Fig.3 Simple diagram of input shaft force analysis

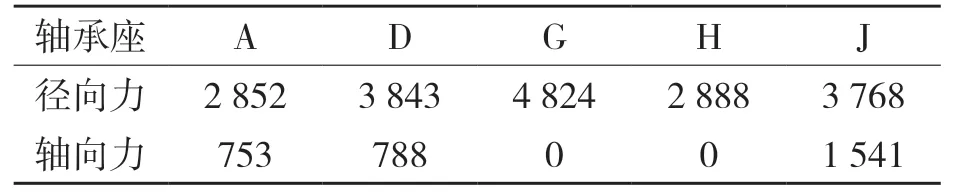
表1 各軸承座支反力載荷(N)Tab.1 Reaction force load of each bearing block (N)

通過上述對各個傳動軸所受載荷大小的計算，得到各軸承座所承受的載荷，軸承座處承受一個徑向合力FR和一個軸向力。徑向合力作用在軸承上，通過軸承以分布壓力載荷的形式作用在軸承座上，在以下分析過程中，作用于軸承座上的徑向載荷按照余弦函數分布在以豎直方向為中心的兩側各60°范圍內[3]。作用在軸承座上的余弦規律載荷分布如圖4 所示。

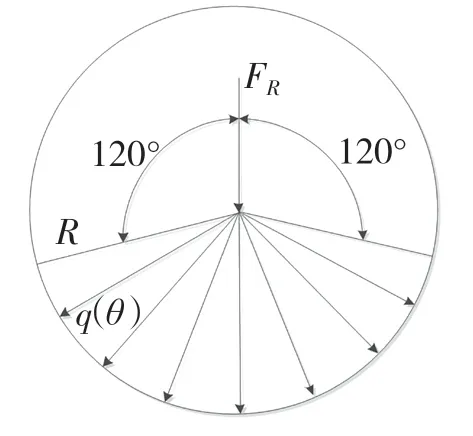
圖4 軸承座徑向壓力載荷余弦函數分布Fig.4 Distribution of cosine function of radial pressure load of bearing block

圖4 中：θ——弧度；FR——在軸承孔處施加的徑向載荷；R——軸承孔處的圓弧半徑。

假設在α 弧度范圍內，在軸承孔寬度為W的圓弧范圍上施加余弦載荷[3]。分布載荷公式為

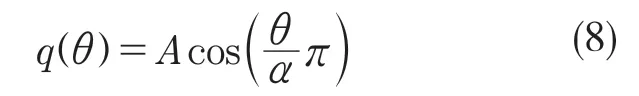
最后可得軸承孔余弦載荷分布形式為

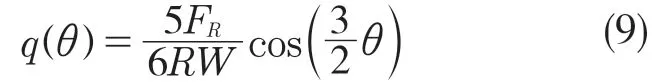
3 有限元建模

3.1 簡化模型

在建立殼體的有限元模型時，應該簡化對殼體強度影響較小的部位，如去除非關鍵部位的過渡圓角，只保留受力較大的軸承座附近的圓角特征，并去掉螺栓孔上的螺紋及倒角。

3.2 設置材料屬性

電機-減速一體化殼體采用6061-T6 鋁合金材料，其彈性模量為70 MPa，泊松比為0.33，密度為2 700 kg/m3，屈服強度為240 MPa[4]。

3.3 劃分網格

由于電機-減速一體化殼體結構較復雜，六面體網格不容易劃分，因此選用四面體進行劃分網格。為得到比較精確的計算結果，本文選用二階四面體CTETRA 單元對模型進行網格劃分。單元尺寸確定為3 mm，對于承受較大載荷的軸承座及附近區域進行細網格的劃分。檢查網格的質量并改進不合格的單元，網格質量的良好與否將直接影響計算過程能否順利完成，并且也會影響分析結果的精度[5]，因此在網格劃分過程中必須檢查網格的質量，通過改進網格質量使得所有網格符合長寬比（Aspect）、翹曲度（Warpage）、偏斜度（Skew）、雅克比（Jacobian）、內角等標準。本文檢查標準如圖5 所示。

圖5 網格質量檢查標準Fig.5 Grid quality inspection standard

4 邊界條件

電機-減速一體化殼體通過法蘭與驅動橋殼連接，后殼體與電機相連接。因此約束殼體上與驅動橋殼相連接的9 個螺栓孔的所有自由度，考慮到電機剛性較大，約束后殼體與電機連接部位的所有自由度。

在殼體軸承座位置施加分布載荷及相應位置施加位移約束后，最終的有限元模型如圖6 所示。

圖6 殼體有限元模型Fig.6 Shell finite element model

5 結果分析

應用OptiStruct 求解器對有限元模型分析計算，殼體的應力及位移云圖分別如圖7、圖8 所示。

圖7 殼體應力云圖Fig.7 Shell stress cloud diagram

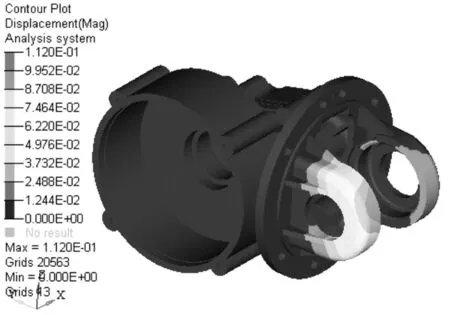
圖8 殼體位移云圖Fig.8 Shell displacement cloud diagram

由應力分布云圖可知，殼體的最大應力為63.3 MPa，位于軸承座J 處。殼體其他區域的應力較小，均在35MPa 以下。

進行靜力分析時，通常取塑性材料的安全系數為1.2～2.5[6]。本文是在電機峰值轉矩下對殼體進行校核，取安全系數為1.5，通過材料許用應力計算公式可知許用應力[σ]=160 MPa。殼體上的最大應力值為63.3 MPa，小于材料的許用應力160 MPa，因此殼體在峰值轉矩工況下滿足強度要求，不會發生屈服失效。

從位移分布云圖可以看出，殼體的最大位移為0.112 mm，根據QC/T 534-1999《汽車驅動橋臺架試驗評價指標》可知，驅動殼體的最大變形必須小于1.5 mm/m。本文中的減速器搭載的樣車的輪距為1 360 mm，計算出殼體的最大變形為0.015 mm/m，滿足性能要求。

6 結論

本文應用有限元分析軟件HyperWorks 對電機-減速一體化殼體進行靜力分析，得到殼體的應力云圖及位移云圖。由云圖可以看出，殼體在極限工況下的最大應力小于材料的許用應力，且具有一定程度的強度余量。殼體的最大位移相對較小，不會影響殼體內部齒輪軸系的正常工作。因此，殼體的強度和剛度均滿足使用要求。