“圓”來如此

蔡雄壯

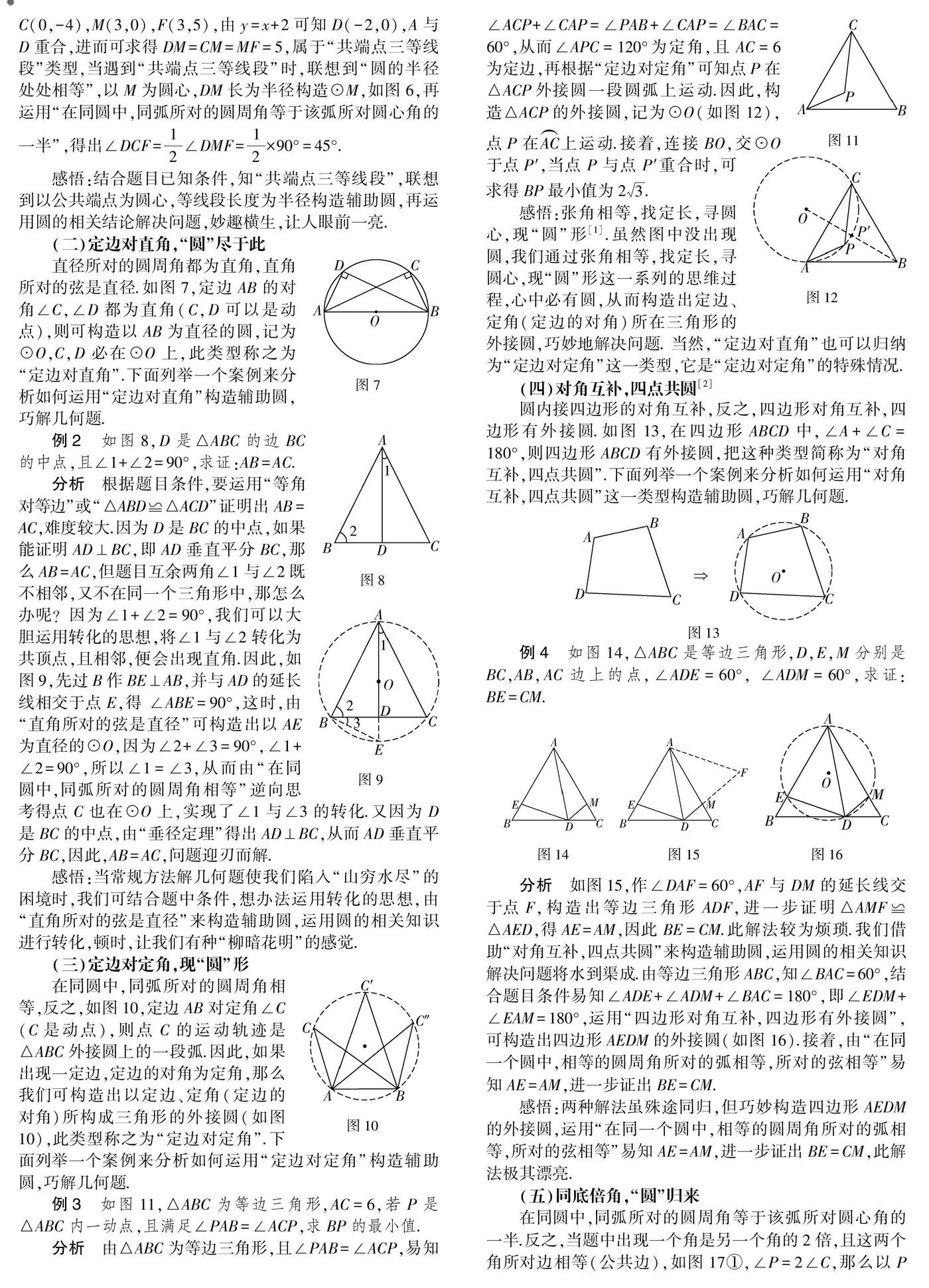
【摘要】構造輔助圓，建立圓的模型，運用圓的相關知識解決幾何問題，化難為易，化隱為顯，會帶來柳暗花明的效果.文章歸納構造輔助圓解幾何題的五種類型以及依據，并列舉案例分析闡述如何運用相應的類型來構造輔助圓解幾何題，從根源上解決學生的困惑，讓學生知其所以然.

【關鍵詞】輔助圓;幾何題;模型;類型

在解幾何題時，經常通過作輔助線，化繁為簡、化難為易，讓題目迎刃而解.對于有些幾何題，相比其他解法，構造輔助圓，建立圓的模型，運用圓的相關知識解決問題，會帶來意想不到的效果，驚嘆構造輔助圓的妙處.

一、由一道模擬題引發的思考

課堂上講解一份泉州中考數學模擬卷時，其中一道選擇題，有學生提出不同的解法，并且這種解法簡單、明了，學生容易理解，但如何準確構造出輔助圓是解決問題的關鍵，這引發了筆者的思考.筆者對如何構造出合適的輔助圓進行了深入的探究.

（一）原題呈現

圖1如圖1，在菱形ABCD中，點P是BC邊上的一動點，連接AP，AP的垂直平分線交BD于點G，交AP于點E，在P點由B點向C點（不與C點重合）運動的過程中，∠APG的大小變化情況

是（?? ）.

A.變大?????? B.先變大后變小

C.先變小后變大 D.不變

（二）解法探究

解法一：根據“線段垂直平分線的性質定理”和“角平分線的性質定理”作輔助線.

分析：由“見垂直平分線，連端點，得等線段”，連接GA.由EG垂直平分AP，知GA=GP.由“見角平分線，作雙垂線，得等線段”，及菱形ABCD易知∠ABD=∠CBD，即BD平分∠ABC.因此，過點G作GM⊥BA于M，作GN⊥BC于N，可得GM=GN，如圖2所示，易證Rt△AMG≌Rt△PNG.從而得∠AGM=∠PGN，進而得∠AGP=∠MGN.再由四邊形BMGN內角和為360°，易知∠MGN+∠MBN=180°，而∠MBN為定值，從而∠MGN也是定值的.由∠AGP=∠MGN，知∠AGP也是定值.在等腰三角形AGP中，頂角∠AGP不變，其底角∠APG也不變，故選D.

解法二：根據“圓的定義”構造輔助圓.

分析：“由垂直平分線得等線段”，連接GA，由EG垂直平分AP，知GA=GP，再由“菱形的軸對稱性”，連接CG，知GA=GC，因此，GA=GP=GC，即A，P，C三點到點G的距離相等，由“圓的定義”知A，P，C三點在以G為圓心，AG長為半徑的圓上，因此，構造出輔助圓，如圖3所示.由“在同圓中，同弧所對的圓周角等于該弧所對圓心角的一半”，知∠AGP=2∠ACP.因為在菱形ABCD中，∠ACP不變，所以∠AGP不變，進而知∠APG不變，故選D.

感悟：解法二通過線段垂直平分線的性質定理和菱形的軸對稱性，結合待解決的問題，巧妙地運用圓的定義，構造輔助圓，運用圓的相關知識找到不變角，進而解決問題.兩種解法相比，解法二簡單、明了，給人一種頓悟的感覺，讓人賞心悅目.

在解幾何題中，結合題目條件巧妙地構造輔助圓，建立圓的模型，化繁為簡、化難為易、化隱為顯，會帶領我們走向柳暗花明.但是在解題中，如何構造出輔助圓，這是學生感到困惑的問題，怎樣解決學生的困惑將成為教師關注的焦點.筆者將構造輔助圓解幾何題歸納出五種類型，與學生、教師共同學習、探究.

二、構造輔助圓的幾種類型

圓是一個重要的數學模型，有了圓這個關鍵載體，其豐富的內涵價值可以直接為我們所用，文章歸納五種構造輔助圓的類型，建立圓的模型，運用圓中的相關結論，巧妙地解決幾何問題.

（一）共端點三等線段，“圓”形畢露

圖4圓的集合定義：在同一個平面內，到定點O的距離等于定長r的點的集合，其中定點O叫作圓心，定長r叫作半徑.由定義可知“圓中半徑處處相等”，如圖4所示，已知AB=AC=AD，那么我們聯想到“圓中半徑處處相等”，可巧妙地構造出以A為圓心，AB長為半徑的⊙A，AB，AC，AD三條線段有公共端點A，且AB=AC=AD，這種類型稱為“共端點三等線段”.下面列舉一個案例來分析如何運用“共端點三等線段”構造輔助圓，巧解幾何題.

例1 如圖5，拋物線y=14x2-32x-4與x軸交于A，B兩點，與y軸交于點C，對稱軸與x軸交于點M，直線y=x+2與拋物線交于點D，E（D在E的左側），與拋物線的對稱軸交于點F，求∠DCF的大小.

分析 由y=14x2-32x-4易求出A（-2，0），B（8，0），C（0，-4），M（3，0），F（3，5），由y=x+2可知D（-2，0），A與D重合，進而可求得DM=CM=MF=5，屬于“共端點三等線段”類型，當遇到“共端點三等線段”時，聯想到“圓的半徑處處相等”，以M為圓心，DM長為半徑構造⊙M，如圖6，再運用“在同圓中，同弧所對的圓周角等于該弧所對圓心角的一半”，得出∠DCF=12∠DMF=12×90°=45°.

感悟：結合題目已知條件，知“共端點三等線段”，聯想到以公共端點為圓心，等線段長度為半徑構造輔助圓，再運用圓的相關結論解決問題，妙趣橫生，讓人眼前一亮.

（二）定邊對直角，“圓”盡于此

圖7直徑所對的圓周角都為直角，直角所對的弦是直徑.如圖7，定邊AB的對角∠C，∠D都為直角（C，D可以是動點），則可構造以AB為直徑的圓，記為⊙O，C，D必在⊙O上，此類型稱之為“定邊對直角”.下面列舉一個案例來分析如何運用“定邊對直角”構造輔助圓，巧解幾何題.

圖8例2 如圖8，D是△ABC的邊BC的中點，且∠1+∠2=90°，求證：AB=AC.

分析 根據題目條件，要運用“等角對等邊”或“△ABD≌△ACD”證明出AB=AC，難度較大.因為D是BC的中點，如果能證明AD⊥BC，即AD垂直平分BC，那么AB=AC，但題目互余兩角∠1與∠2既不相鄰，又不在同一個三角形中，那怎么辦呢？因為∠1+∠2=90°，我們可以大膽運用轉化的思想，將∠1與∠2轉化為共頂點，且相鄰，便會出現直角.因此，如圖9，先過B作BE⊥AB，并與AD的延長線相交于點E，得 ∠ABE=90°，這時，由“直角所對的弦是直徑”可構造出以AE為直徑的⊙O，因為∠2+∠3=90°，∠1+∠2=90°，所以∠1=∠3，從而由“在同圓中，同弧所對的圓周角相等”逆向思考得點C也在⊙O上，實現了∠1與∠3的轉化.又因為D是BC的中點，由“垂徑定理”得出AD⊥BC，從而AD垂直平分BC，因此，AB=AC，問題迎刃而解.

感悟：當常規方法解幾何題使我們陷入“山窮水盡”的困境時，我們可結合題中條件，想辦法運用轉化的思想，由“直角所對的弦是直徑”來構造輔助圓，運用圓的相關知識進行轉化，頓時，讓我們有種“柳暗花明”的感覺.

（三）定邊對定角，現“圓”形

圖10在同圓中，同弧所對的圓周角相等，反之，如圖10，定邊AB對定角∠C（C是動點），則點C的運動軌跡是△ABC外接圓上的一段弧.因此，如果出現一定邊，定邊的對角為定角，那么我們可構造出以定邊、定角（定邊的對角）所構成三角形的外接圓（如圖10），此類型稱之為“定邊對定角”.下面列舉一個案例來分析如何運用“定邊對定角”構造輔助圓，巧解幾何題.

例3 如圖11，△ABC為等邊三角形，AC=6，若P是△ABC內一動點，且滿足∠PAB=∠ACP，求BP的最小值.

分析 由△ABC為等邊三角形，且∠PAB=∠ACP，易知∠ACP+∠CAP=∠PAB+∠CAP=∠BAC=60°，從而∠APC=120°為定角，且AC=6為定邊，再根據“定邊對定角”可知點P在△ACP外接圓一段圓弧上運動.因此，構造△ACP的外接圓，記為⊙O（如圖12），點P在AC上運動.接著，連接BO，交⊙O于點P′，當點P與點P′重合時，可求得BP最小值為23.

感悟：張角相等，找定長，尋圓心，現“圓”形[1].雖然圖中沒出現圓，我們通過張角相等，找定長，尋圓心，現“圓”形這一系列的思維過程，心中必有圓，從而構造出定邊、定角（定邊的對角）所在三角形的外接圓，巧妙地解決問題. 當然，“定邊對直角”也可以歸納為“定邊對定角”這一類型，它是“定邊對定角”的特殊情況.

（四）對角互補，四點共圓[2]

圓內接四邊形的對角互補，反之，四邊形對角互補，四邊形有外接圓.如圖13，在四邊形ABCD中，∠A+∠C=180°，則四邊形ABCD有外接圓，把這種類型簡稱為“對角互補，四點共圓”.下面列舉一個案例來分析如何運用“對角互補，四點共圓”這一類型構造輔助圓，巧解幾何題.

例4 如圖14，△ABC是等邊三角形，D，E，M分別是BC，AB，AC邊上的點，∠ADE=60°， ∠ADM=60°，求證：BE=CM.

分析 如圖15，作∠DAF=60°，AF與DM的延長線交于點F，構造出等邊三角形ADF，進一步證明△AMF≌△AED，得AE=AM，因此BE=CM.此解法較為煩瑣.我們借助“對角互補，四點共圓”來構造輔助圓，運用圓的相關知識解決問題將水到渠成.由等邊三角形ABC，知∠BAC=60°，結合題目條件易知∠ADE+∠ADM+∠BAC=180°，即∠EDM+∠EAM=180°，運用“四邊形對角互補，四邊形有外接圓”，可構造出四邊形AEDM的外接圓（如圖16）.接著，由“在同一個圓中，相等的圓周角所對的弧相等，所對的弦相等”易知AE=AM，進一步證出BE=CM.

感悟：兩種解法雖殊途同歸，但巧妙構造四邊形AEDM的外接圓，運用“在同一個圓中，相等的圓周角所對的弧相等，所對的弦相等”易知AE=AM，進一步證出BE=CM，此解法極其漂亮.

（五）同底倍角，“圓”歸來

在同圓中，同弧所對的圓周角等于該弧所對圓心角的一半.反之，當題中出現一個角是另一個角的2倍，且這兩個角所對邊相等（公共邊），如圖17①，∠P=2∠C，那么以P為圓心，PA的長度為半徑，構造出輔助圓（如圖17②），則點C在⊙P上，此種類型稱之為“同底倍角”.下面列舉一個案例來分析如何運用“同底倍角”構造輔助圓，巧解幾何題.

例5 如圖18，以△ABC的邊AB為底作等腰三角形△PAB，且∠P=2∠C，AC與PB交于點D，若PB=4，PD=3，求AD·DC的值.

分析 題目中出現∠P=2∠C，且PA=PB，∠P與∠C所對的邊相同（公共邊），可以聯想到“在同圓中，同弧所對的圓周角等于該弧所對圓心角的一半”，運用“同底倍角”這一類型來構造輔助圓，如圖19，以P為圓心，PB的長度為半徑作圓，并延長BP交⊙P于點Q，連接AQ，易知∠C=∠Q，從而得△BDC∽△ADQ，可得BDAD=CDQD，即CD·AD=BD·QD，易知BD=1，QD=7.因此，CD·AD=7.

感悟：本題運用“在同圓中，同弧所對的圓周角等于該弧所對圓心角的一半”，借助“同底倍角”這一類型，構造出輔助圓，運用圓中的知識解決問題，思路精巧，方法獨特，但需要注意的是題目恰巧PA=PB，點A在此圓上，又由∠P=2∠C，可知點C也在圓上，其間的細節還有待我們仔細琢磨.

三、“圓”來如此

以上歸納出構造輔助圓解幾何題的五種類型，并列舉案例分析闡述如何運用相應的類型來構造輔助圓，妙解幾何題.現對這五種類型的知識依據做進一步的概括：運用“共端點三等線段”這一類型構造輔助圓主要的知識依據是圓的定義;運用“定邊對直角”這一類型構造輔助圓主要的知識依據是直徑所對的圓周角都為直角，直角所對的弦是直徑;運用“定邊對定角”這一類型構造輔助圓主要的知識依據是在同圓中，同弧所對的圓周角相等;運用“對角互補，四點共圓”這一類型構造輔助圓主要的知識依據是對角互補的四邊形必有外接圓;運用“同底倍角”這一類型構造輔助圓主要的知識依據是在同圓中，同弧所對的圓周角是該弧所對圓心角的一半.五種類型構造輔助圓，并非無中生有，而是基于學生已扎實掌握圓的相關知識，結合題目已知條件和所要解決的問題進行構造，建立圓的模型，運用圓的相關結論以及其他知識點解決問題.

學生在學習中更需明白其中構造輔助圓的數學原理，知其所以然，真正領會“圓”來如此，才能深知其中的奧妙，做到圖中無圓，心中有圓.

【參考文獻】

[1]沈岳夫.微專題：道是無“圓”卻有“圓”[J].中學數學雜志，2019（06）：50-52.

[2]李昌剛.圖中無圓，心中構圓：談中考壓軸題巧構輔助圓的策略[J].福建中學數學，2018（06）：40-42.