基于灰色預測模型的山東省高考人數的分析與預測

程子超

【摘要】本文使用MATLAB實現灰色預測，對2007年至2019年山東省高考人數進行分析和計算，得到了預測山東省高考人數的灰色系統中GM（1，1）模型.該灰色預測模型合理性通過了檢驗，最后利用所得到的模型預測出未來5年山東省高考人數呈緩慢下降的趨勢.同時，在分析模型時，發現高考人數與對應高考年份18年前的出生人數具有一定相關性的規律.

【關鍵詞】MATLAB;灰色預測;山東省;高考人數

“每一代青年都有自己的際遇和機緣，都要在自己所處的時代條件下謀劃人生、創造歷史.”[1]當今社會，青年實現理想的有效途徑之一就是參加高考，跨入大學校門，接受高等教育，為實現人生價值積蓄能量，回報父母和祖國.高考一直是牽動中國千家萬戶的大事，2019年全國高考報名人數已經達到1031萬，創造歷史新高.山東省作為人口大省，也是高考大省，多年來高考報名人數位居全國前列.在查閱相關資料時發現，研究高考改革方向的學術文章較多[2，3]，探究未來高考人數趨勢方面的研究較少.本文通過建立灰色預測模型來預測未來5年山東省高考人數，為廣大山東考生、家長、教育機構提供有效參考.

一、灰色預測模型的構建

1.主要研究的樣本數據和方法

數據選取2007—2019年山東省高考報名人數，具體數據見表1.

2.GM（1，1）模型的原理

灰色預測是“通過鑒別系統因素之間發展趨勢的相異程度，生成有較強規律性的數據序列，然后建立相應的微分方程模型，從而預測事物未來的發展趨勢.在諸多的灰色模型中，以灰色系統中單序列一階線性微分方程GM（1，1）模型最為常用.” [4]

第一，將原始數據x（0）={x（0）（1），x（0）（2），…，x（0）（n）}（n為數據個數）累加以便弱化隨機序列的波動性和隨機性，得到新數據序列：x（1）={x（1）（1），x（1）（2），…，x（1）（n）}，建立x（1）（t）的一階線性微分方程

dx（1）dt+ax（1）=u.（1）

其中，a，u為待定系數，分別稱為發展系數和灰色常用量，求解a，u構成的矩陣.

u^=au=BTB-1BTYn.（2）

其中，B與常數項Yn為累加生成數據做均值產生的變量.再將u^代入式（1），并求解，將結果x^（1）t+1=x（0）（1）-uae-at+ua及x^（1）（t）進行離散并將二者作差以還原x^（0）原序列.

第二，對建立的灰色模型進行檢驗精密度，若精密度較高，則輸出結果：

x^（0）=x^（0）（1），x^（0）（2），…，x^（0）（n），x^（0）n+1，…，x^（0）n+m.

其中前n項為原數列的模擬，后m項為未來數列的模擬.

3.GM（1，1）灰色預測模型對山東省高考人數的分析

因為灰色預測中矩陣運算較多，而MATLAB可以很高效地進行計算，所以MATLAB是實現灰色預測的首選.

依據原理編寫并運行程序，得到的預測數據如下：

‘Prediction=

77.6000 69.6412 67.7547 65.9194 64.1337 62.3964 60.7062 59.0618 57.4619 55.9053 54.3909 53.4176 51.4841 50.0895 48.7326 47.4125 46.1282 44.8787 43.6630 42.4802

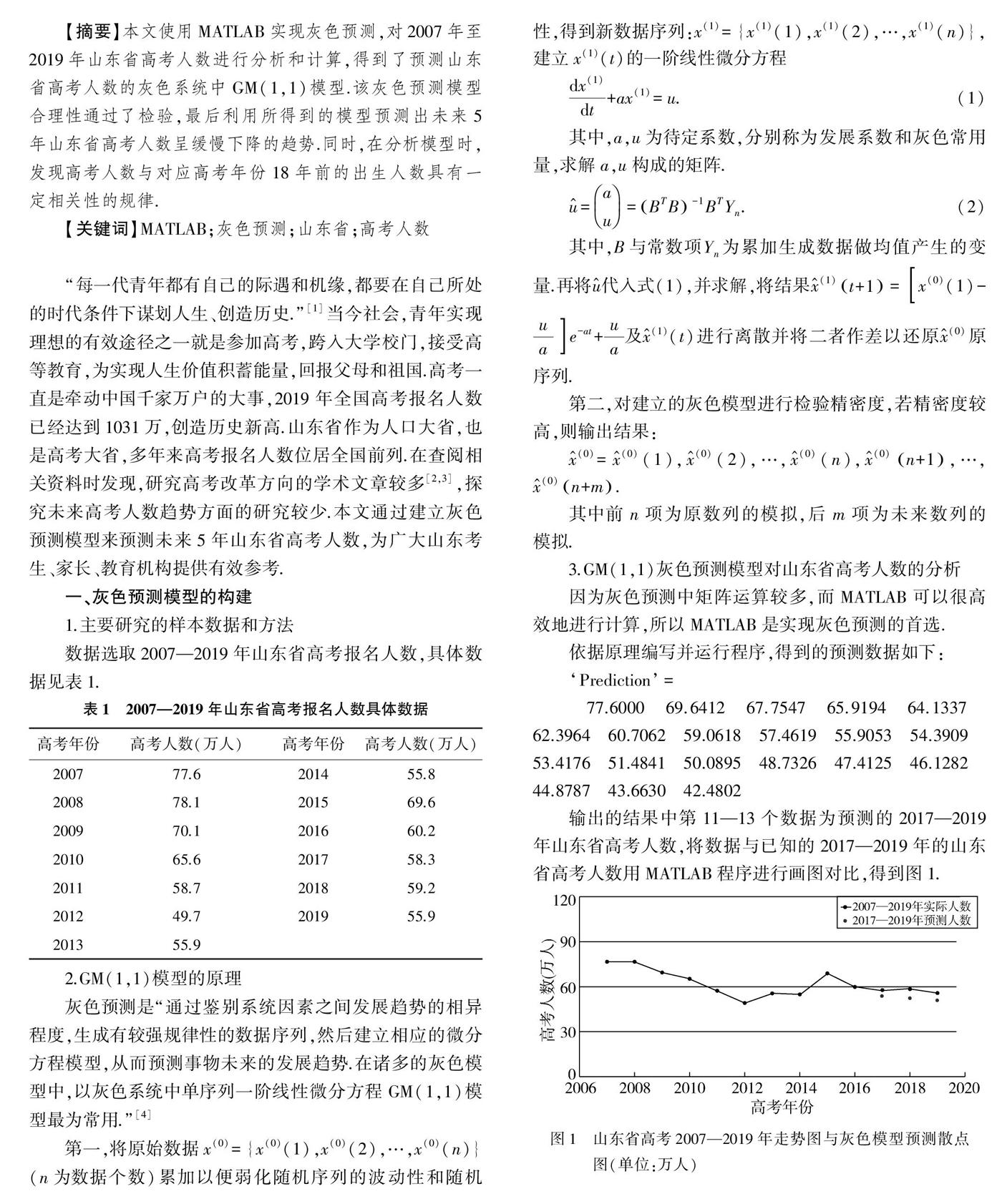
輸出的結果中第11—13個數據為預測的2017—2019年山東省高考人數，將數據與已知的2017—2019年的山東省高考人數用MATLAB程序進行畫圖對比，得到圖1.

圖1 山東省高考2007—2019年走勢圖與灰色模型預測散點圖（單位：萬人）

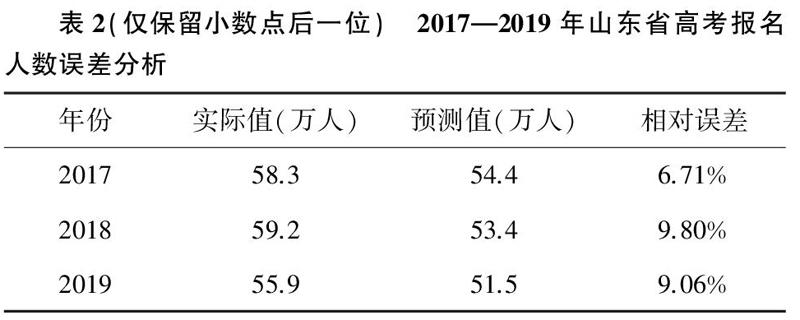
由表2可知灰色預測中預測2017—2019的數據與實際數據變化趨勢和數值均相近，這表明通過預測的數據可信度較大，可以繼續通過該模型預測未來的山東省高考報名人數.

二、灰色模型的預測及建議

1.對未來5年的山東省高考報名人數的預測

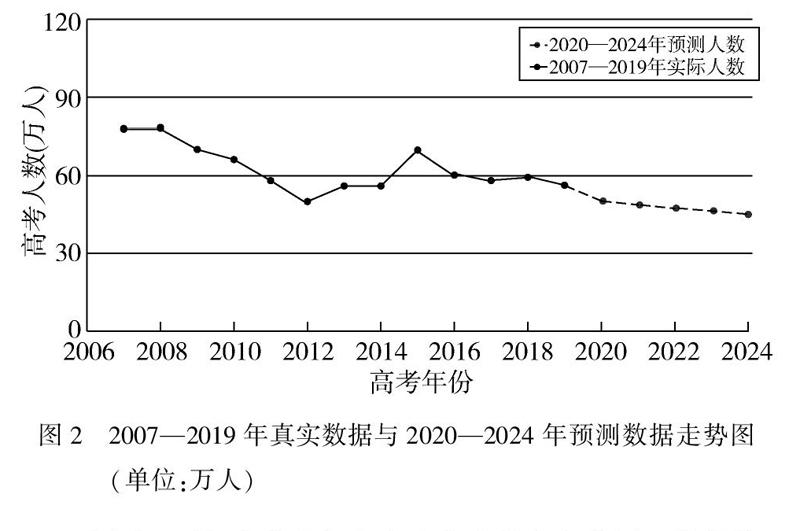
為保證精確度，只預測未來五年的山東省高考報名人數.在上述程序運行后輸出的結果中第14—18個數據為預測的2020—2024年山東省高考人數，再通過MATLAB畫圖與2007—2019年的數據對比進行預測并分析.

圖2 2007—2019年真實數據與2020—2024年預測數據走勢圖（單位：萬人）

由圖2可知未來幾年山東省高考報名人數呈下降趨勢.這表明在未來5年山東省高考人數會緩慢持續下降.

2.對于灰色預測模型的建議

由表2知建立的模型的最大相對誤差為9.80%，可知歷年高考人數并不是單純的函數關系，而是由眾多影響因素所綜合決定的.在此僅分析一項因素——對應高考年份18年前的出生人數，將數據用MATLAB繪成圖像.（定義“對應年份”，對應年份為實際年份18年前的年份，例如，2003年對應年份為1985年，2019年對應年份為2001年）

圖3 2003—2019年對應年份出生人數走勢圖與2003—2019年高考人數梯形圖（單位：萬人）

由圖3可知二者的波動趨勢相近，表明二者有一定的相關性.通過對應年份出生人數與高考人數之比R繪圖分析.

圖4 2003—2019年對應年份出生人數與高考人數之比R走勢圖

由圖4可知R雖然存在波動，但是波動逐漸減小，最終穩定在1.26.說明對應年份出生人數是最主要影響因素之一，且相關性隨時間在不斷增大.但受制于灰色理論GM（1，1）本身的局限性，無法進一步探究.建議在未來使用更加先進、科學的模型進行預測.

三、小 結

本文依據灰色理論，利用2007—2019年山東省高考報名人數，通過建立基于MATLAB下灰色預測的山東省高考人數模型，對于模型的擬合度進行了驗證，并得出擬合度較高，可以較精確預測未來的結論.在此基礎上，利用該模型對2020—2024年的山東省高考報名人數進行了預測，預測結果為未來5年山東省高考報名人數會逐漸減少.同時，分析出對應年份的出生人數與高考報名人數有一定的相關性，且在近十年相關性增大.

【參考文獻】

[1]習近平.青年要自覺踐行社會主義核心價值觀-在北京大學師生座談會上的講話[N].人民日報，2014-5-5（1）.

[2]張明坤.山東省高考錄取機制改革與應對[J].中國成人教育，2018（18）：78-81.

[3]張明遠，高洋.山東省高考制度改革，機遇與挑戰并存[J].教育觀察，2019（05）： 51-52.

[4]卓金武，王鴻鈞.MATLAB數學建模方法與實踐：第3版[M].北京： 北京航空航天大學出版社，2018.