考慮蠕變作用的2.25Cr-1Mo-V鋼加氫反應器設計方法

萬里平,李 宇

(中國石化工程建設有限公司,北京 100101)

0 引言

加氫反應器等高溫設備通常采用高強度抗氫腐蝕的鉻鉬鋼，成本較高。近年出現的2.25Cr-1Mo-V(SA-182 F22V,以下簡稱加釩鋼)許用應力較鉻鉬鋼大幅提升，見表1。這對操作壓力和溫度要求更高的反應器是很好的選擇，可大幅降低壁厚。隨著反應器的規模擴大，對于上千萬噸的漿態床加氫反應器沸騰床加氫反應器及渣油加氫反應器等，輕量化設計舉足輕重，因此加釩鋼在國產加氫反應器中的應用日益增多[1-5]。加氫反應器承受苛刻載荷，需采用分析方法設計。加氫反應器設計的難點很多，本文僅討論反應器殼體結構的設計。

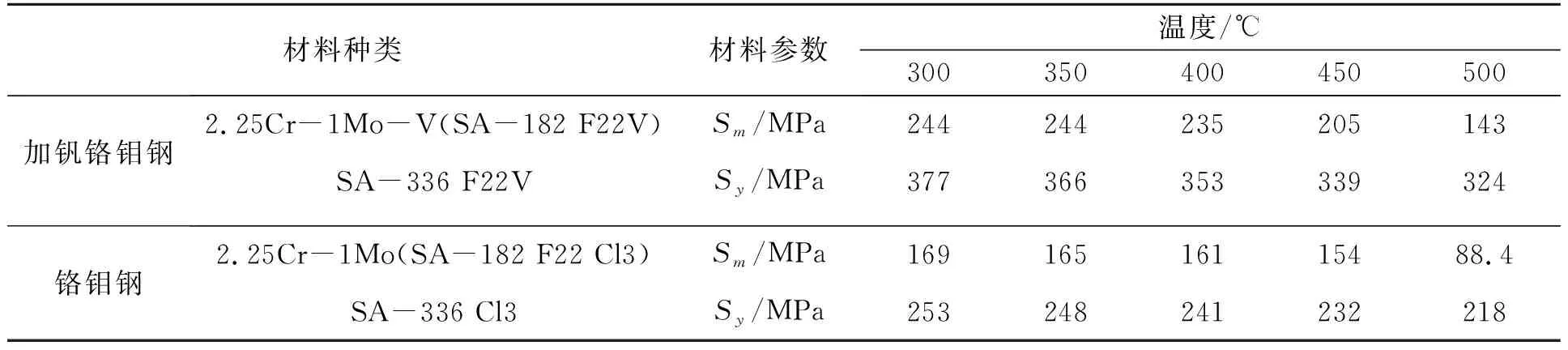
表1 不同溫度下的許用應力與屈服強度Tab.1 Allowable stress and yield stress at different temperatures

1 加釩鉻鉬鋼加氫反應器設計方法介紹

加釩鋼在400 ℃以上的許用應力主要由與時間相關的材料參數控制，Sy為屈服強度。2.25Cr-1Mo-V許用應力隨溫度的變化曲線見圖1。可以看出，許用應力Sm在400 ℃之后有明顯下降。

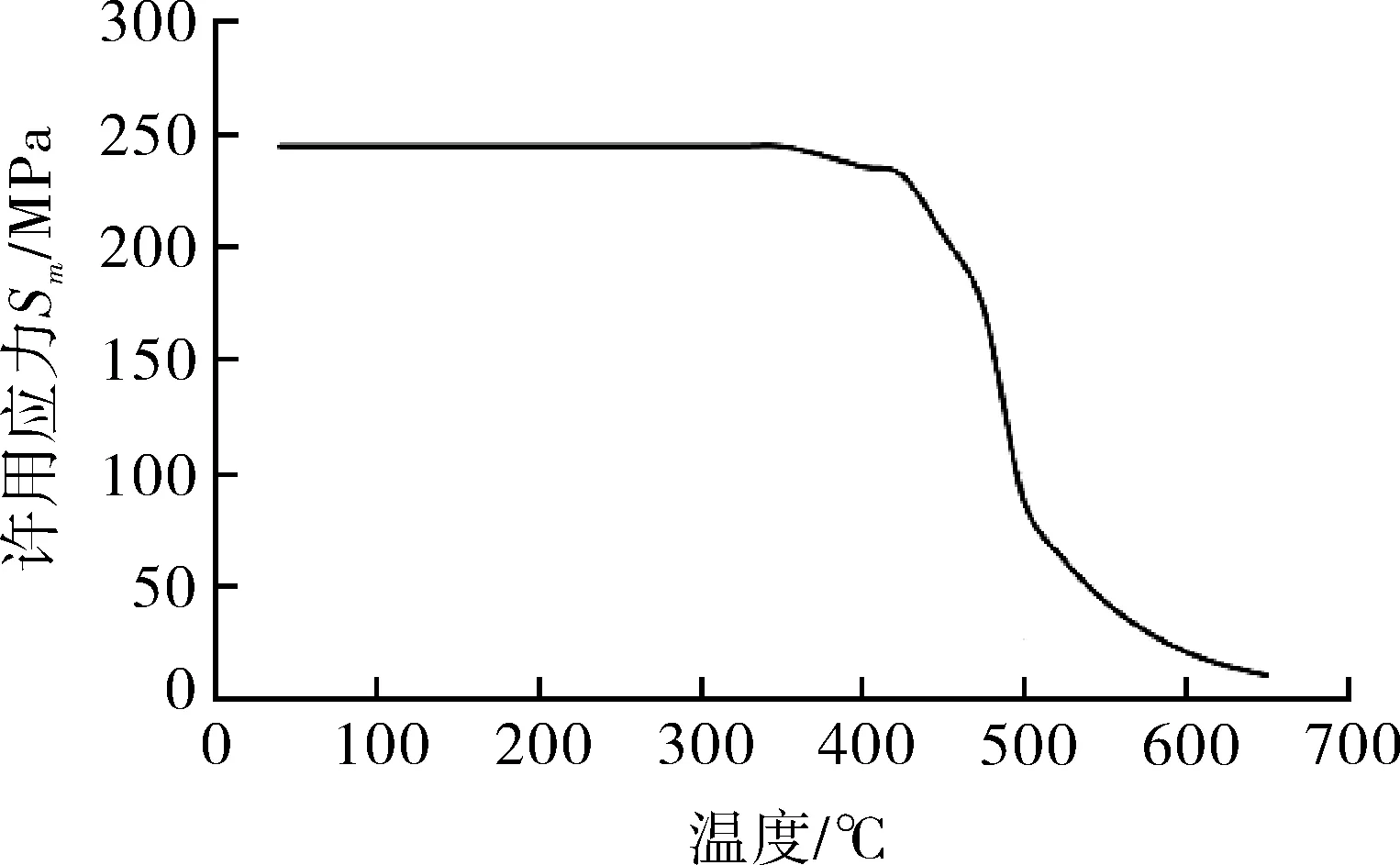
圖1 2.25Cr-1Mo-V許用應力隨溫度的變化曲線

國內常規設計規范GB/T 150.1～150.4—2011《壓力容器》引入試件發生1%蠕變和斷裂持久極限的強度參數對材料許用應力進行限制。分析設計規范JB 4732—1995《鋼制壓力容器——分析設計標準》無相應的蠕變和蠕變疲勞校核方法，新版標準正在修訂，送審稿第5部分引入了兩種高溫蠕變分析方法，其中方法A與ASME Code Case 2605-3(以下簡稱CC2605-3)相似，方法B與ASME Code Case 2843相似，單就適用材料和溫度看，均可用于加氫反應器的設計。

1.1 目前常見的彈性分析方法

加氫反應器最大應力通常出現在頂部人孔、熱電偶口、裙座過渡段等部位，設計時主要關注其強度問題，選用與蠕變和持續斷裂相關的許用應力以保證設計安全,基本設計思路如下：(1)初步確定殼體和接管的壁厚；(2)對應力集中區域采用彈性應力分析+應力分類法，進行塑性垮塌和安定性校核。

1.2 蠕變疲勞校核方法

蠕變本構方程眾多，比較有代表性的有NORTON[6]本構方程，PRAGER[7]提出的Omega方程，BAKER等[8]提出的方程等。CC2605-3采用的Omega方程見式(1)，描述蠕變變形的第二和第三階段。該方法并非強制要求，但國外業主通常要求必須采用。

(1)

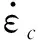
CC2605-3需進行4種失效模式的校核：防止塑性垮塌、防止棘輪、防止蠕變疲勞、防止外壓屈曲。首先根據用戶說明書確定最苛刻的應力和溫度對應的工況，其中設計工況用于校核塑性垮塌，操作工況用于校核棘輪和蠕變疲勞，根據不同情況選擇Option1或Option2方案，兩種方案對應的校核要求不同。CC2605-3允許采用彈性分析方法校核棘輪，見式(2)。

PL+Pb+Q+F≤(Sh+Syc)

(2)

采用理想彈塑性應力應變曲線和Omega方程計算蠕變率和蠕變損傷，進而得到純蠕變壽命，由當量應力幅查得允許循環次數，從而得到蠕變疲勞壽命。CC2605-3校核流程在文獻[9-10]有詳細介紹，這里不再贅述。

2 加釩鋼加氫反應器算例的討論

2.1 彈性分析方法

采用彈性分析設計的某4臺加釩鋼加氫反應器(由于技術保密，對工藝條件進行合理調整)，設計壽命30年，開停工循環次數為30次(每年停工檢修1次)。最大應力出現在頂部人孔，熱電偶口，裙座與筒體連接處(見圖2)。由于國內項目遵循的分析設計標準是JB 4732，本節采用第三強度理論。各部位在設計和操作工況下的SINT應力如表2所示。

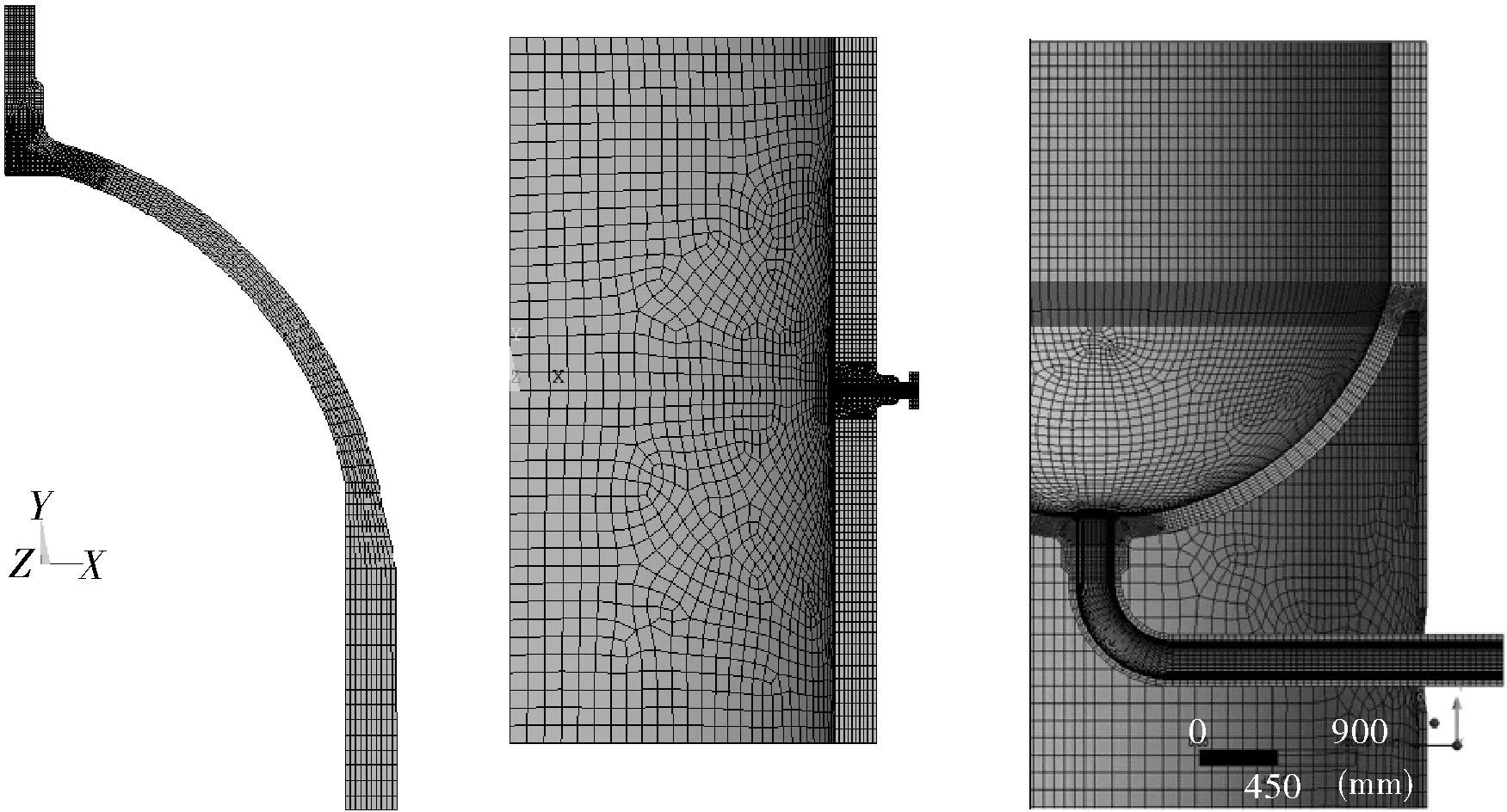
圖2 反應器頂部人孔、熱電偶口及裙座與筒體連接處的網格模型Fig.2 The mesh model of manhole,thermocouple port andconnection of shell and skirt at top of the reactor

表2 4臺加釩鋼反應器的彈性分析結果Tab.2 The elasticity analysis results of 4 vanadium-containing hydrogenation reactors

從表2可以看出，熱電偶開口處的應力強度最大，頂部人孔應力最小。其中，第2臺反應器的操作條件最苛刻，以該反應器為例，對應力強度最小的頂部人孔和應力最大的熱電偶口進行校核。

(1)塑性垮塌校核。

設計工況下，人孔、熱電偶口的SINT云圖及線性化路徑SCL_1～SCL_10見圖3,4。

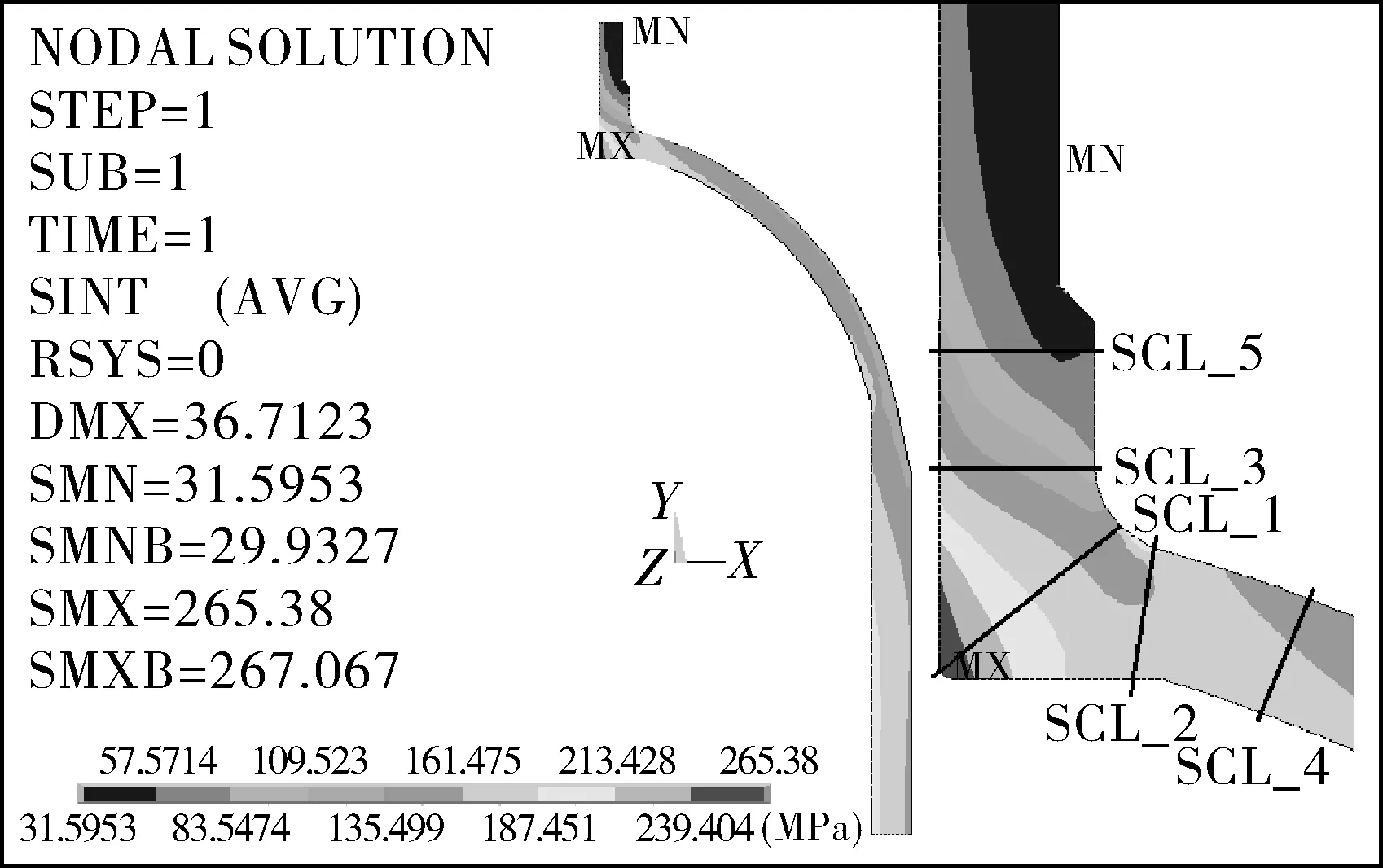
圖3 頂部人孔設計工況下的應力強度云圖及線性化路徑示意Fig.3 The stress intensity nephogram and schematic diagramof linearization path of manhole under design condition

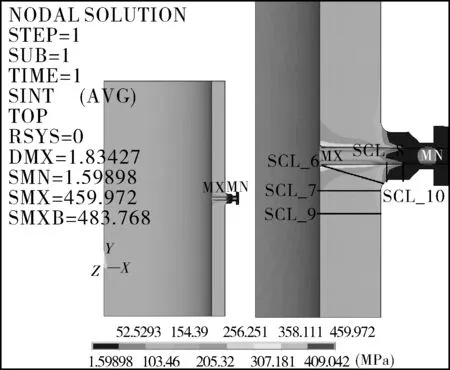
圖4 熱電偶口設計工況下的應力強度云圖及線性化路徑示意Fig.4 The stress intensity nephogram and schematic diagramof linearization path of thermocouple under design condition

(2)安定性校核。

安定性校核基于操作工況，由于溫差應力非常小，因此采用設計工況的結果等比例折算。

從表3校核結果可以看出，塑性垮塌的評定和安定性校核設計余量都較大。

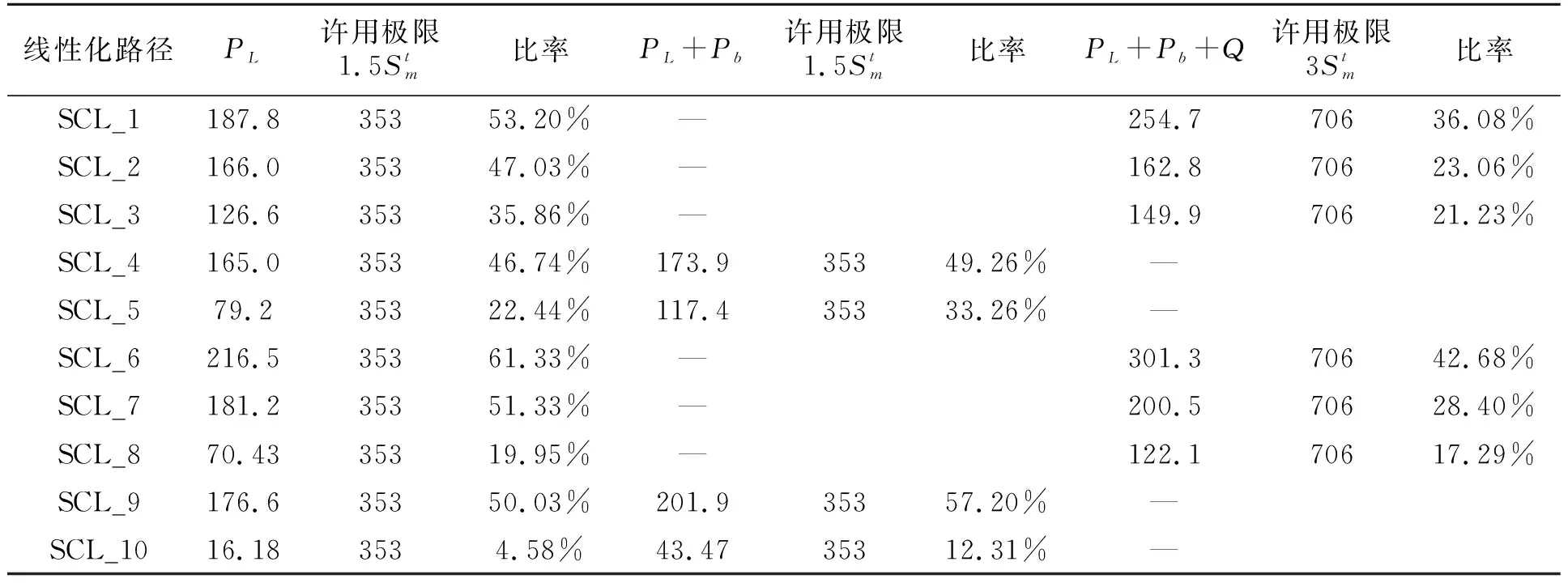
表3 第2臺反應器的應力校核結果Tab.3 Stress check results of the second reactor MPa

2.2 CC2605-3的非彈性方法

與第2.1節相同，選取第2臺反應器的頂部人孔和熱電偶口作為研究對象。根據CC2605-3(b)和(c)的要求，塑性垮塌校核與第2.1節(1)相同，這里重點介紹棘輪評定和蠕變疲勞評定。CC2605-3(d)(1)中Option1要求采用最苛刻的溫度和壓力組合，設置3個完整循環，每個循環在操作溫度下保載8 725 h(即1年時間)，如圖5所示。

圖5 載荷隨時間變化曲線(含3次完整循環)Fig.5 Variation curve of load with time(Including 3 complete cycles)

2.2.1 棘輪校核

經過3次循環，在圖6中的A點(人孔接管內倒角)，B點(熱電偶口內倒角)取得應力應變曲線，見圖7，8。

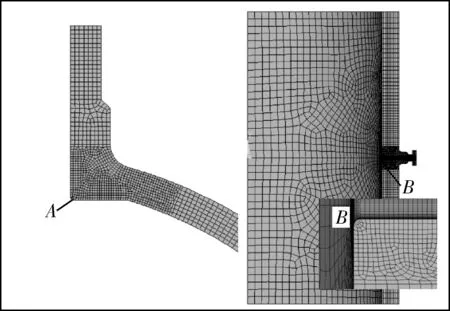
圖6 點A和點B示意圖Fig.6 Schematic diagram of point A and B

由圖7可以看出，人孔的A點，3次循環過程均未發現非彈性行為，棘輪校核通過。由于最大應力強度僅248 MPa，遠低于該溫度下的屈服強度353 MPa，保載時間內蠕變應變很小，應力松弛不明顯。由圖8可以看出，熱電偶口的B點，在第一次循環加載過程中產生了塑性屈服，此后兩次加載過程均在彈性范圍內。盡管應力強度達到了屈服強度353 MPa，但在操作溫度400 ℃下，應力松弛也不明顯。經過3次循環，A點的非彈性應變最大值1.79×10-7mm/mm，B點的非彈性應變最大值3.32×10-4mm/mm，均小于CC2605-3中表2的限值，滿足規范中(d)(6)(a)的要求。因此棘輪校核通過。

圖7 3次循環載荷作用下A點的應力-應變曲線Fig.7 Stress-strain curve of point A under 3 cyclic loads

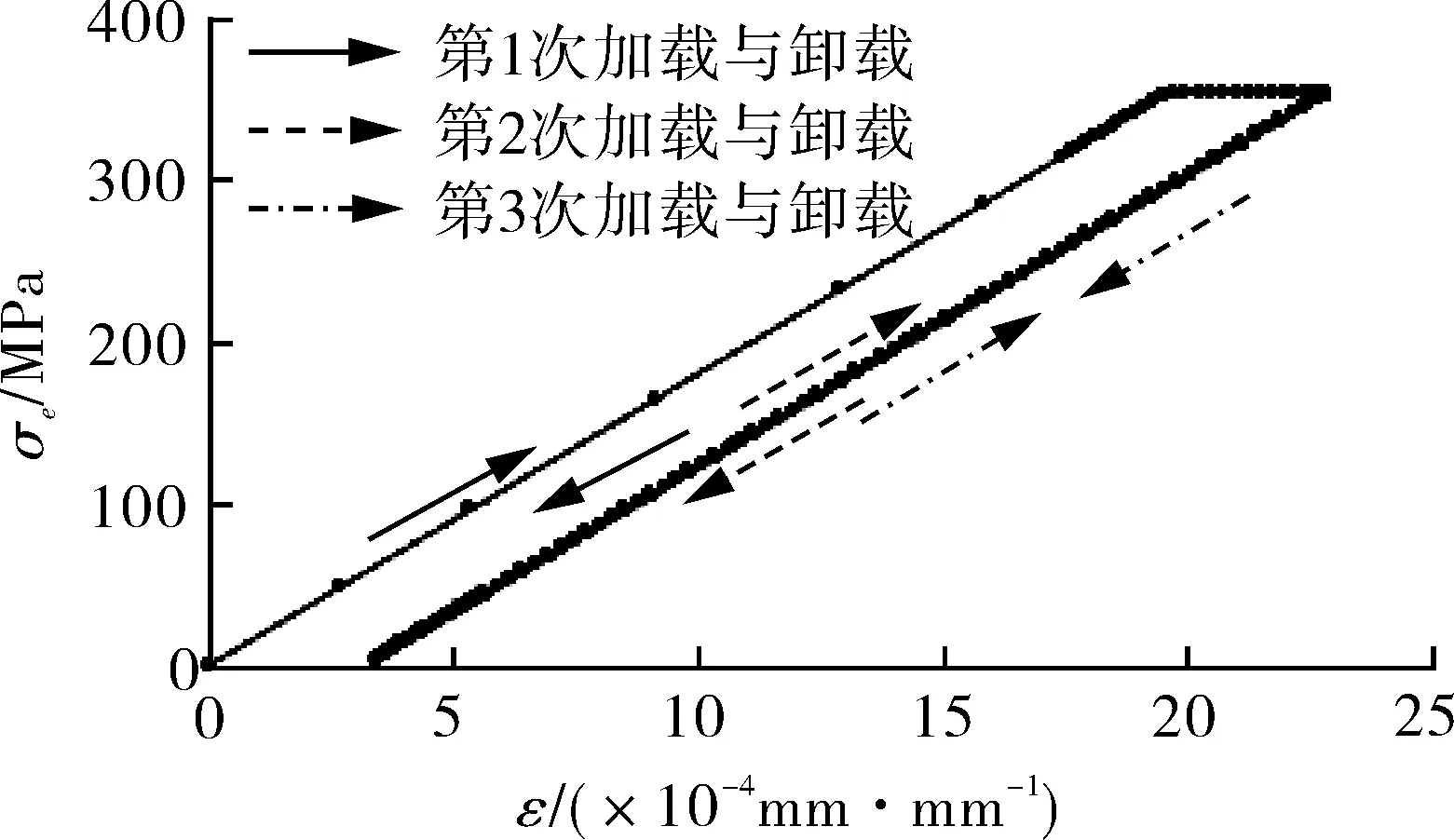
圖8 3次循環載荷作用下B點的應力-應變曲線Fig.8 Stress-strain curve of point B under 3 cyclic loads

第1.2節已經介紹過，對于棘輪的校核還可采用彈性分析，通過式(2)進行校核，這里不再贅述。

2.2.2 蠕變疲勞校核

(1)確定純蠕變壽命。

在操作溫度400 ℃和操作壓力19.22 MPa下保載1×106h，頂部人孔點A的蠕變損傷DC=0.023<0.95(見圖9)，純蠕變壽命Lcaf=1×106h。經過3.17×105h，熱電偶口點B的DC達到0.95(見圖10)，該處Lcaf為3.17×105h。

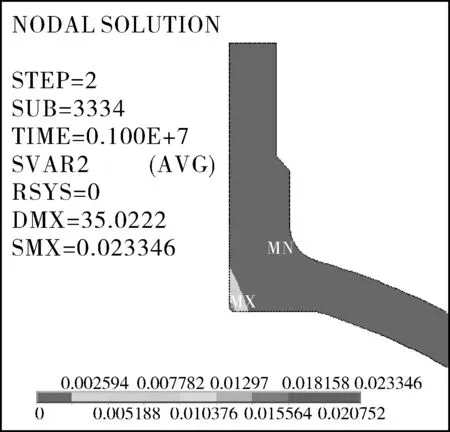
圖9 1×106 h后頂部人孔模型的蠕變損傷云圖Fig.9 Creep damage nephogram of top manhole modelafter 1×106 h

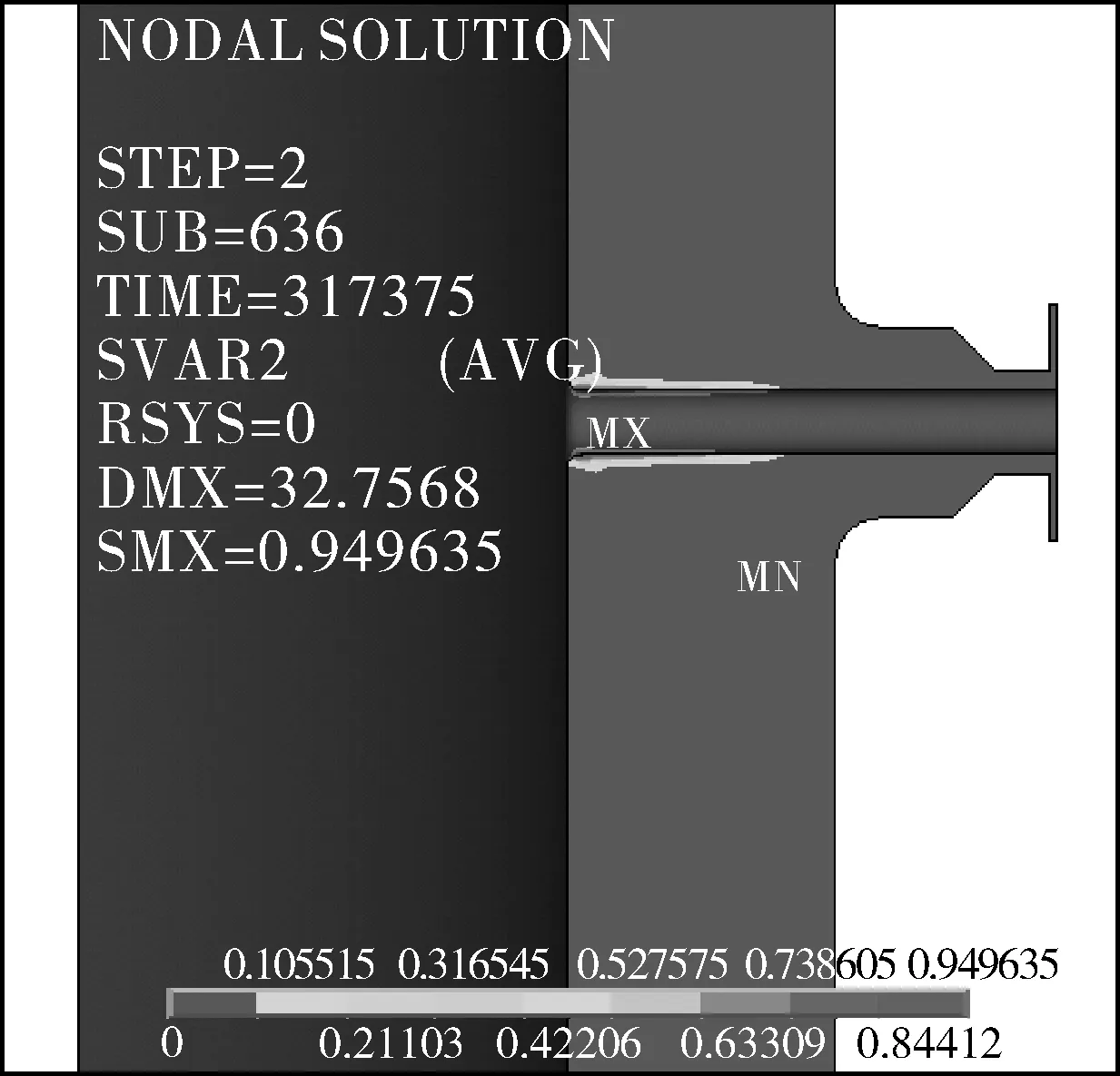
圖10 3.17×105 h后熱電偶模型的蠕變損傷云圖Fig.10 Creep damage nephogram of thermocouple modelafter 3.17×105 h

(a)

(b)圖11 人孔在操作壓力19.22 MPa下的應力強度云圖和靜水壓云圖Fig.11 Stress intensity nephogram and hydrostatic stress nephogram of manhole under the operating pressure of 19.22 MPa

(2)校核蠕變疲勞壽命。

根據CC2605-3式(15)和式(16)，A點操作壓力下的當量應力幅為123.35 MPa，Δεeqv=0,允許循環次數N=29 891，大于實際循環次數30次，Lcwf=Lcaf=1×106h，大于設計壽命2.628×105h。B點操作壓力下當量應力幅為229.9 MPa，Δεeqv=0.000 004 97，N=418，大于實際循環次數30次，Lcwf=3.16×105h，大于設計壽命2.628×105h。

因此，兩者蠕變疲勞校核通過。

2.3 對兩種方法計算結果的分析

彈性分析方法設計的典型部位余量較大，尤其是頂部人孔。熱電偶口開孔率很小，但開孔內壁出現了較大的應力集中，對于蠕變疲勞壽命的影響非常大。

由第2.2節可知，對于頂部人孔，操作壓力產生的最大應力約248 MPa，尚未屈服，溫度400 ℃對應的蠕變損傷非常小，蠕變疲勞校核余量很大。對于熱電偶口，B點進入屈服，400 ℃的操作溫度下保載3.17×105萬h后，蠕變損傷就達到了0.95。以上的分析可知，對于彈性虛擬應力超過屈服強度的部位，應特別注意其蠕變疲勞的校核。

文中案例是近年來國內加氫裝置的典型加釩鋼加氫反應器，本節對其中設計條件較苛刻的一臺補充了蠕變疲勞校核，發現該反應器具有一定設計余量，這也側面說明，由于設計時留有足夠的安全余量，近年來設計的加釩鋼加氫反應器在使用中通常不會出現蠕變失效問題。

3 操作溫度和操作壓力對蠕變參數的影響

3.1 同一操作溫度不同操作壓力對蠕變參數的影響

文獻[11]指出，三軸度系數(σe/p)較大的點是蠕變疲勞校核的危險點。以人孔為例，操作溫度400 ℃，操作壓力19.22 MPa時，應力強度σe云圖及靜水壓p云圖見圖11。最大應力強度σe出現在A點，最大靜水壓p出現在A′點。逐漸加大操作內壓，從19.22 MPa增至19.22×2.0 MPa，表4列出A點附近與A′點附近的σe和p及σe/p的數據。

表4 人孔在不同操作壓力作用下的σe，p及σe/pFig.4 σe,p,σe/p of manhole under action of different operating pressure MPa

A點的σe/p始終大于A′點。從第2.2節可知，經過3次循環，A點的蠕變損傷大于A′點。隨著內壓增加，應力強度σe和靜水壓p等比例增加，σe/p保持不變，當內壓增至27.68 MPa(19.22×1.44)，A點率先進入屈服，繼續增大內壓，A點的σe保持不變，而p繼續增加，當A′點直到內壓達到36.52 MPa(19.22×1.9)左右時才進入屈服。

可以看到，表征危險點的σe/p在彈性狀態和彈塑性狀態下，其數值是變化的，在彈性狀態下，每個部位的σe/p保持不變，一次加載即可找到危險點。但若操作壓力使得結構進入彈塑性狀態，危險點可能變化。

3.2 同一操作壓力不同操作溫度對蠕變參數的影響

蠕變應變εc是蠕變損傷Dc的函數，而Dc是應力強度σe，靜水壓p，操作溫度T和時間增量t的函數，即Dc=f(σe,p,T,t)。已知σe和p，可以通過CC2605-3中的式(3)～(14)得到某時間增量下的Dc。隨著應力松弛的持續，σe和p逐漸下降。

圖13示出了操作溫度390 ℃下，B點的Dc實際模擬值和公式估算值的對比。表5為公式計算過程的示范。可以看出，隨保載時間的增加，實際模擬的Dc始終低于公式估算值。采用公式計算得到的純蠕變壽命必定大于實際考慮蠕變松弛的純蠕變壽命，使用該壽命進行蠕變疲勞校核是保守和安全的。

圖13 實際模擬與公式估算的蠕變損傷Dc隨時間變化的對比Fig.13 Comparison of variations of creep damage Dcactually simulated and estimated by formula with time

表5 公式計算的蠕變損傷Tab.5 Creep damage calculated by formula

4 Omega方法的工程簡化

彈性分析在加氫反應器設計中已非常成熟，而CC2605-3需編寫子程序，有一定難度。彈性分析是一次加載，而CC2605-3需要計算成千上萬個載荷步，尤其是節點較多的三維模型(如文中熱電偶口)，對計算機要求很高，工程中實施起來費時費力。

加氫反應器的操作壓力通常為15～20 MPa，操作溫度為380～440 ℃,運行過程中一般不會出現復雜的載荷波動。由于這個特點，可以將CC2605-3進行合理簡化。CC2605-3的重點是棘輪和蠕變疲勞的校核。其中，棘輪可以通過彈性分析校核。蠕變疲勞校核要點是計算蠕變疲勞壽命Lcwf。采用初始σe和p，通過公式計算Lcwf和允許循環次數N，進行蠕變疲勞的初步評估，是保守而安全的。若蠕變疲勞校核非設計文件要求必須完成，可以通過如下步驟，對結構合理性進行預判或保守地回避完整的蠕變疲勞校核。

(1)初步確定結構尺寸，在設計壓力和設計溫度下，采用彈性分析方法[12-13]，進行塑性垮塌校核；

(2)采用CC2605-3中(d)(1)Option1的方法確定最苛刻的操作載荷，通過彈性分析方法和式(2)進行棘輪校核，采用彈塑性分析方法，獲得三軸度系數較大的危險點的σe和p；

(3)采用CC2605-3中的式(3)～式(14)，計算(2)中危險點的純蠕變壽命Lcaf；

(4)求得危險點的當量應力幅，通過CC2605-3中表3M和表4求得允許循環次數N及當量應變幅Δεeqv，得到蠕變疲勞壽命Lcwf。

若棘輪或蠕變疲勞校核不通過，則調整結構，重新校核。如此，無需調用蠕變子程序，僅進行簡單易行的彈性分析和彈塑性分析，即可保守得到允許循環次數N和蠕變疲勞壽命Lcwf，降低了設計難度。

5 結語

首先介紹了加釩鋼加氫反應器常用的彈性分析方法和CC2605-3進行蠕變疲勞校核的流程。以國內某臺反應器為例，對頂部人孔和熱電偶口分別采用兩種方法進行校核，發現反應器雖未進行蠕變疲勞校核，由于彈性分析的設計余量較大，蠕變疲勞校核是合格的，并且指出雖然熱電偶口開口率較小，但由于內倒角附近存在非常大的應力集中，極大降低了該處的蠕變疲勞壽命，在未來的設計中應優化結構，降低這類結構的應力集中。

研究了操作溫度和操作壓力對于蠕變參數的影響。若某操作壓力使得結構處于彈性狀態，通過一次加載的彈性分析可確定三軸度系數較大的危險點，若操作壓力使結構進入塑性，則隨著保載的持續，三軸度系數較大點的位置可能變化。若結構處于彈性狀態，對于加氫反應器常見的操作溫度，蠕變疲勞壽命通常較大，如本文中的人孔結構；若結構進入塑性，隨溫度的增加，蠕變疲勞壽命會迅速下降，且此時由于當量應力幅較大，允許循環次數較小。此時需優化結構形式，改善應力集中，提高蠕變疲勞壽命。

最后對CC2605-3中的重難點進行歸納，提出采用彈性分析和彈塑性分析方法，利用初始σe和p，通過公式保守估算蠕變疲勞壽命。在非必需進行蠕變疲勞分析的項目中，這樣的簡化回避了編寫蠕變子程序和計算機硬件不足的困難，方便工程人員進行蠕變疲勞壽命預估，可快速預判結構設計是否安全合理。