基于延性耗竭模型的邊緣型穿透多裂紋干涉與合并分析

齊 磊，張學偉，溫建鋒

(華東理工大學 機械與動力工程學院 承壓系統與安全教育部重點實驗室,上海 200237)

0 引言

現役工程結構中，經常發現多個裂紋共存的情況，如管道、壓力容器及焊縫接頭等[1-5]。根據裂紋尺寸和相對距離不同，相鄰的多裂紋可能以單裂紋不干涉的形式獨立擴展；也可能相互干涉進而合并成大裂紋繼續擴展[6-7]。與此同時，多裂紋的干涉效應會顯著影響實際工程構件的承載能力。由于問題的復雜性，采用斷裂力學方法來預測多裂紋的干涉與合并行為仍是一項困難的工作。

針對多裂紋共存的情況，現有的合乎使用(Fitness-For-Service,FFS)規范(例如ASME BPVC Ⅺ—2019《鍋爐及壓力容器》、BS 7910：2019《金屬結構中缺陷驗收評定方法指南》、API 579 / ASME FFS-1：2016《合乎使用》、GB/T 19624—2019《在用含缺陷壓力容器安全評定》等)已提出多種共線和合并準則。這些合并準則通常基于經驗或裂紋尖端斷裂參量的增量來制定[8]。表1列出現有FFS規范中用于評估兩個穿透裂紋的共線與合并準則。可以發現，這些合并準則都是簡單地通過評估裂紋之間的尺寸或距離是否滿足指定的條件，從而來判斷多個裂紋是否可以合并成一個大的裂紋。值得注意的是，不同的評定標準或規范會給出不同的評估結果[9]，并且現有的規范可能給出不準確的評估結果[10]。另外，TU等[11]進行了含二維非共面裂紋試樣的疲勞試驗，并提出表面多裂紋合并準則。MIYAZAKI等[12]對含有多個穿透裂紋的延性鋼板進行一系列的斷裂破壞試驗，根據試驗測得的最大載荷提出了極限載荷預測公式。之后，HASEGAWA等[13-15]進行了含周向多裂紋的管道試驗，并提出了多裂紋共線與合并準則。但是，這些新的合并準則僅由少量試驗驗證，對于普遍情況的適用性尚不清楚。

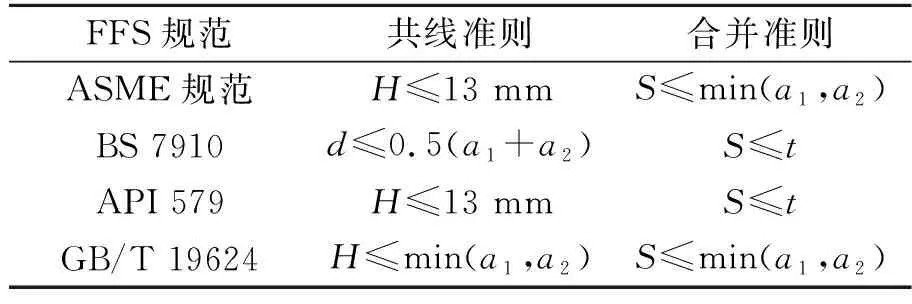
表1 FFS規范中用于評估兩個穿透裂紋的共線與合并準則Tab.1 Alignment and coalescence rules used to assesstwo through-wall cracks in FFS codes

目前，國內外學者對含有多裂紋的構件也進行了許多數值模擬研究。不同的數值模擬方法被用來研究含裂紋構件的延性斷裂行為，如擴展有限元法(XFEM)、廣義有限元法(GFEM)和蒙特卡羅(Monte Carlo)模擬法等。例如，BIDOKHTI等[9]采用擴展有限元方法研究了含兩個偏置穿透裂紋板的裂紋擴展和干涉合并行為，并提出了新的裂紋合并評估準則。O’HARA等[16]基于廣義有限元法，研究了表面多裂紋的干涉與合并行為，并給出基于廣義有限元法研究多裂紋相互作用的有效性和適用性。ZHU等[17]采用蒙特卡羅模擬與試驗數據相結合的方法，建立了一種模擬表面多裂紋擴展和合并的概率方法，并給出了試樣從初始狀態到臨界狀態的剩余使用壽命。隨著數值模擬技術的發展，采用連續損傷力學理論結合有限元的方法[18-20]，開始廣泛應用于研究多裂紋的干涉與合并行為，并且已經給出多種預測模型與極限載荷公式[21-23]。例如，KIM等[6]采用修正應力斷裂應變損傷模型，預測了含有內部穿透多裂紋的平板及含有表面多裂紋管道的最大載荷及裂紋合并載荷。ZHANG等[24]進行了含平行偏置穿透裂紋平板的拉伸試驗，初步驗證了考慮非單調斷裂應變軌跡關系的延性損傷分析方法的有效性。WEN等[25-27]分別在疲勞、蠕變作用下，研究表面或埋藏多裂紋的擴展行為及干涉效應，并提出了采用新的裂紋合并準則來評估多裂紋的相互作用。然而，這些數值模擬方法或缺乏試驗的驗證、或無法準確預測裂紋的干涉與合并行為。因此，進一步預測多裂紋的干涉與合并行為，還需要進行更深入的數值研究工作。

本文基于延性耗竭理論的簡單損傷模型，并結合三種斷裂應變軌跡關系，模擬含有邊緣型穿透多裂紋的平板試樣的延性斷裂行為，將模擬結果與試驗結果以及基于FFS規范評定的結果進行對比，并比較幾何模型應力狀態假設對預測結果的影響。

1 試驗數據

為了研究穿透裂紋的干涉與合并行為，HASEGAWA等對一系列含有兩個邊緣型穿透裂紋平板試樣進行了拉伸試驗，試樣材料為低碳鋼JIS SM400A。KIM等在文獻[6]中給出了Hasegawa等進行的含有兩個邊緣性穿透裂紋平板試樣的拉伸試驗結果。含有邊緣型穿透裂紋平板試樣的結構見圖1，試樣寬度50 mm，厚度5.7 mm。

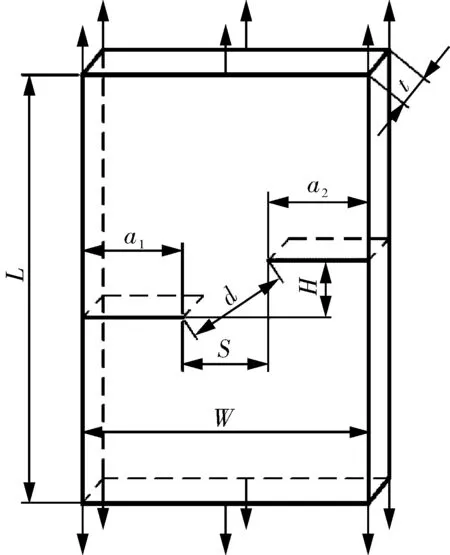
圖1 含兩個邊緣型穿透裂紋平板試樣結構示意Fig.1 Schematic diagram of flat plate specimen withtwo edge through-wall cracks

利用電火花線切割方法在試樣上預制兩個邊緣型穿透裂紋，裂紋長度a1,a2尺寸相等且隨兩個裂紋之間橫向距離S和豎向距離H變化而變化，試樣尺寸、試驗最大載荷及裂紋合并情況見表2[6]。

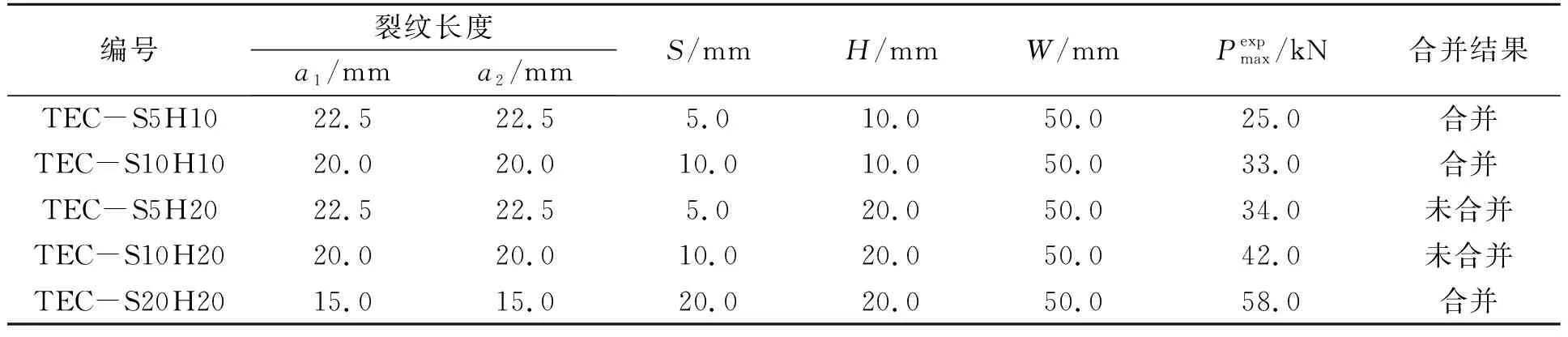
表2 含邊緣型穿透裂紋平板試樣尺寸及拉伸試驗結果Tab.2 Summary of dimensions and tensile experiment results of flat plate specimen with two edge through-wall cracks

2 有限元分析

2.1 材料參數與力學性能

假定材料為各向同性硬化的彈塑性材料，并遵從J2塑性流動法則，HASEGAWA等通過對平板試樣(厚度5.7 mm，寬度12.5 mm)進行室溫下拉伸試驗，獲得了材料的拉伸力學性能，如表3[6]所示。為了描述材料的塑性變形行為，在有限元分析中需要提供真應力-應變關系，通過對拉伸試驗數據進行處理獲得了頸縮前的真應力-應變關系，隨后利用Swift硬化定律[28]對試驗數據進行擬合，以外推到更大的應變水平，即：

表3 SM400A材料的拉伸力學性能和材料參數Tab.3 Tensile mechanical properties and material parameters for SM400A

σtrue=A(εture+ε0)N

(1)

式中,σtrue為真應力;εtrue為真應變;A,ε0,N為材料參數。

擬合得到的參數如表3所示，SM400A材料的真應力-應變關系如圖2[6]所示。

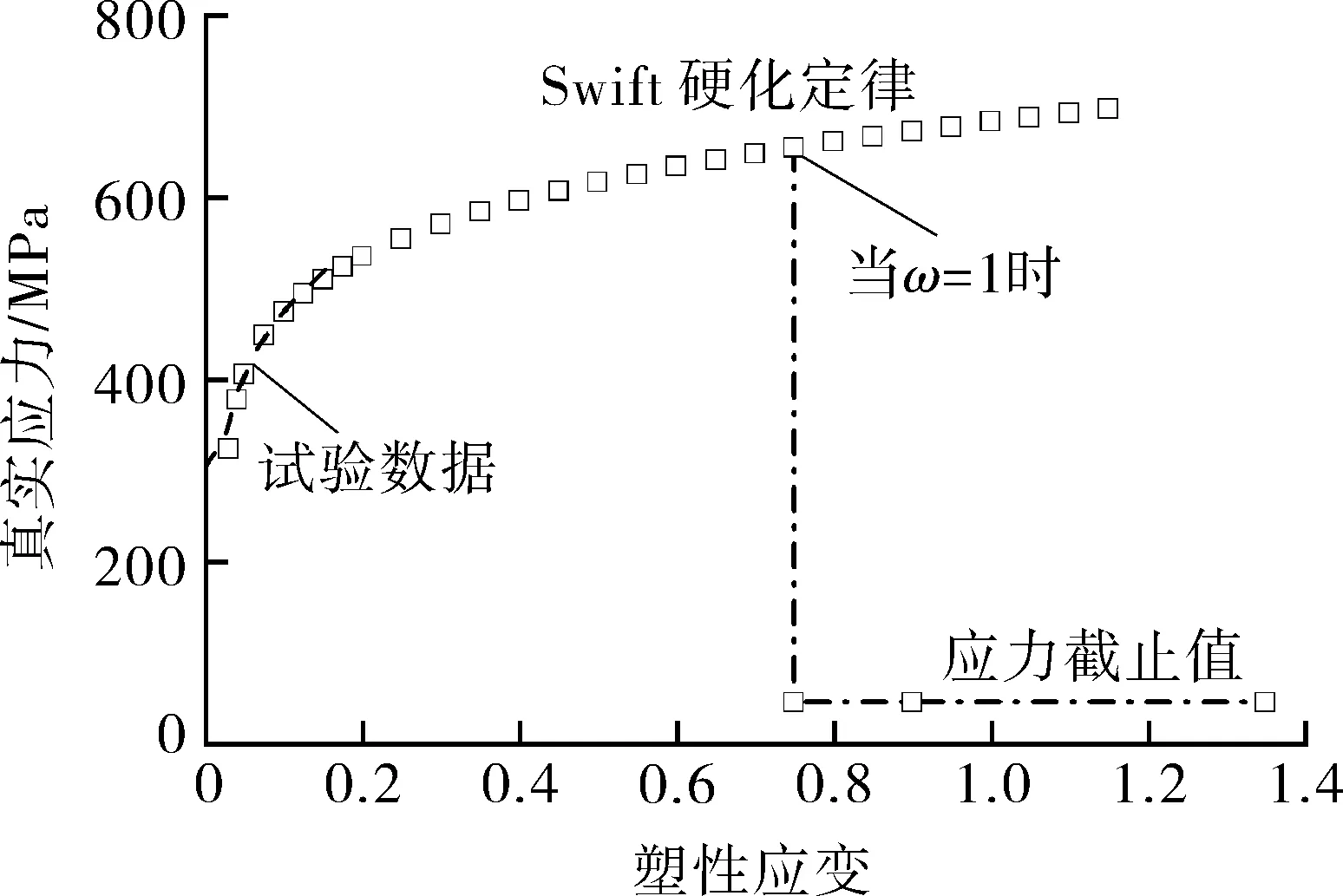
圖2 SM400A材料的真應力-應變曲線和應力釋放示意Fig.2 True stress-strain curves and schematic diagram ofstress release of SM400A

2.2 損傷演化模型

應力狀態一般用應力三軸度η來表征，定義為：

η=σm/σe

(2)

式中，σm為平均應力;σe為von Mises等效應力。

平均應力σm為：

(3)

式中，σi，σ2，σ3代表3個主應力。

von Mises等效應力σe為：

(4)

在整個加載過程中，應力三軸度的值并不是恒定的，通常用平均三軸度ηave來定量描述變形過程中的應力三軸度，定義為：

(5)

式中，εf為等效塑性斷裂應變；εp為等效塑性應變。

模擬中使用的損傷演化模型是基于延性耗竭概念建立的。文獻[3,19,29]也采用了類似的損傷演化模型。通過定義一個參數ω來定量描述加載過程中的累積損傷量。損傷增量Δω定義為等效塑性應變增量Δεp和等效塑性斷裂應變εf的比值，即：

Δω=Δεp/εf

(6)

利用簡單的線性損傷累積規則來計算損傷參數ω，表達式如下：

(7)

當ω=1時，認為發生延性破壞，相應的單元失去承載能力，即裂紋出現擴展。這一過程可以通過將高斯積分點處的所有應力分量減小到一個非常小的值實現，本文通過修改屈服面的方式來實現這一過程，以避免將所有應力分量減小到零后可能會導致數值不收斂的問題。因此，本文將應力截止值取為抗拉強度值的10%，應力釋放的示意如圖2所示。

在ABAQUS軟件中，應用兩個用戶子程序實現上述過程。第一個是用于計算損傷增量和累積損傷量的子程序USDFLD；然后，累積損傷量通過狀態變量傳遞到第二個子程序UHARD，當累積損傷量達到1時，通過改變屈服面的方式將所有應力分量急劇減小到應力截止值。

2.3 斷裂應變軌跡

延性斷裂破壞強烈依賴于應力狀態，并且在不同的應力三軸度下會有不同的失效機制[30-32]。因此，考慮不同的斷裂應變軌跡是準確預測結構延性斷裂行為的關鍵。在之前的工作[33]中，利用一系列拉伸剪切組合試樣的拉伸試驗結果，已經建立SM400A材料的斷裂應變軌跡，如圖3[6，33]所示，結果發現，等效塑性斷裂應變與平均應力三軸度之間呈現非單調的關系，通過對試驗結果進行擬合，獲得非單調斷裂應變軌跡如式(8)所示。

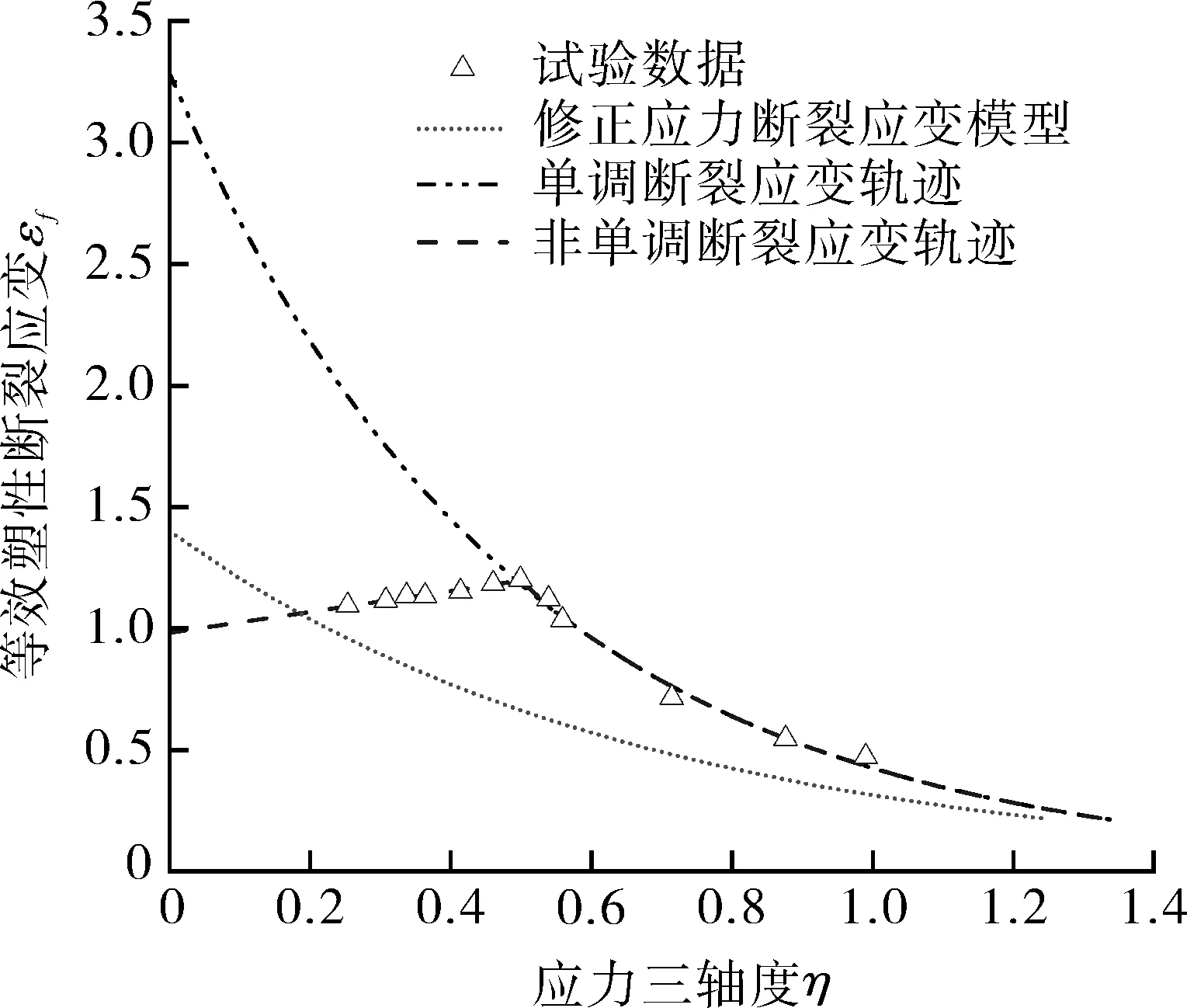
圖3 SM400A材料不同斷裂應變軌跡Fig.3 Different fracture strain locus for SM400A

(8)

εf=3.29exp(-0.25ηave) (ηave≥0)

(9)

(10)

為了進行對比，本文還采用了另外兩種斷裂應變軌跡關系，一種是單調斷裂應變軌跡關系，其斷裂應變隨平均應力三軸度的增加呈指數減少，如式(9)所示；另一種斷裂應變軌跡關系是文獻[6]提出的修正應力斷裂應變模型，是基于斷裂應變與初始應力三軸度呈現指數函數的關系，如式(10)所示。圖3也給出了單調斷裂應變軌跡和修正應力斷裂應變模型的變化曲線。

2.4 有限元模型建立

利用ABAQUS軟件[34]對含兩個邊緣型穿透裂紋的平板試樣進行數值模擬分析。利用模型和載荷的對稱性，采用1/2的3D幾何模型建模，并采用Seam方式創建裂紋。平板一端完全固定；另一端進行位移加載。為了保證數值計算結果的準確性，對裂紋附近的網格進行細化，最小網格尺寸約為0.4 mm×0.4 mm×0.4 mm，裂紋尖端的網格細節如圖4所示，單元類型為C3D8。另外，本文還采用二維幾何模型建模，在不同應力狀態假設條件下，對試樣進行有限元模擬分析。

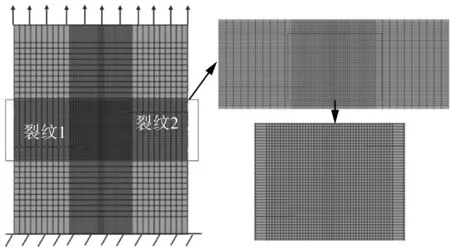
圖4 含兩個邊緣型穿透裂紋平板試樣的有限元網格Fig.4 Finite element mesh of flat plate specimen withtwo edge through-wall cracks

3 結果與討論

3.1 有限元數值模擬結果

采用結合非單調斷裂應變軌跡的損傷演化模型對含有邊緣型穿透裂紋進行了數值模擬，有限元模擬結果與試驗結果對比見表4，可以看出，有限元模擬預測結果與試驗結果吻合較好，說明采用非單調斷裂應變軌跡的有限元模擬可以準確預測裂紋干涉與合并行為。對于TEC-S5H10，TEC-S10H10和TEC-S20H20試樣，有限元分析結果表明，兩裂紋最終發生了合并；對于TEC-S5H20和TEC-S10H20試樣，裂紋未發生合并。此外，現有的FFS規范中，在某些情況下無法準確預測裂紋的合并，例如，對于TEC-S20H20試樣的兩個穿透裂紋，基于所有FFS規范中的共線與合并準則而得到的評估結果都是未合并，然而試驗結果卻是合并的，這說明FFS規范中的共線與合并準則給出了非保守的評估結果。另外，對于TEC-S5H20試樣，BS 7910和GB/T 19624—2019標準的評估結果認為兩個裂紋發生合并，而試驗結果是未發生合并，說明這兩個規范給出了保守的評估結果。因此，現有的FFS規范中的共線與合并準則可能不足以預測裂紋干涉與合并行為。相比之下，本文采用非單調斷裂應變軌跡得到的預測結果明顯優于基于現有的FFS規范中的共線與合并準則得到的評估結果。

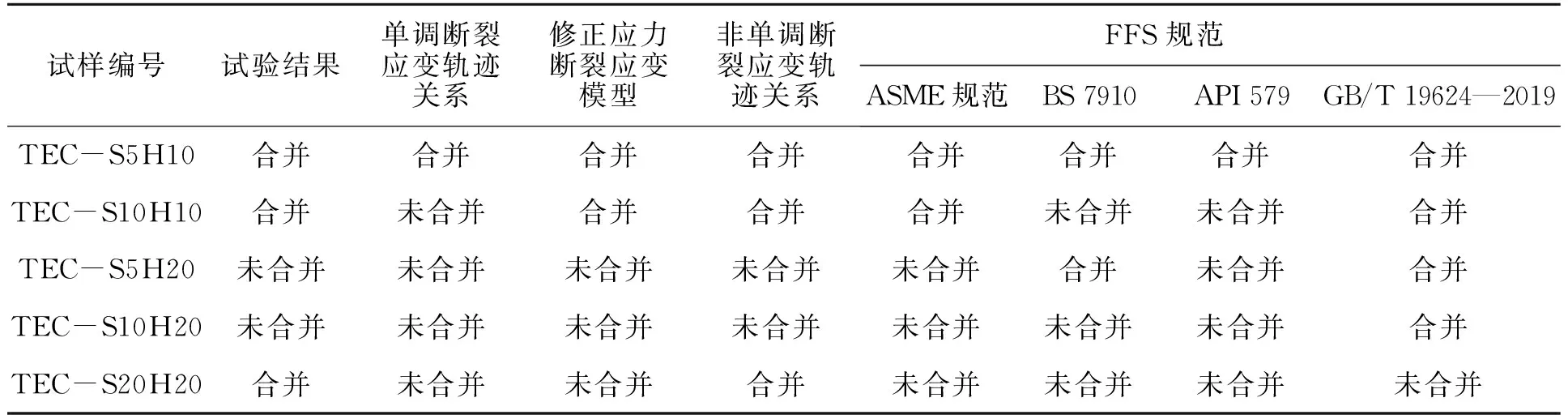
表4 裂紋合并試驗結果與采用不同斷裂應變軌跡關系預測結果以及基于FFS規范得到的裂紋評估結果之間的對比Tab.4 Comparisons among experimental results of crack coalescence,simulation results predicted by different fracture strainlocus and evaluation results obtained based on FFS codes

圖5示出試樣的損傷云圖與斷后試樣對比，可以更直觀地發現有限元預測結果與試驗結果相符。另外，損傷主要集中在兩個裂紋之間。其中，對于TEC-S5H10試樣，兩個裂紋尖端在加載過程中逐漸靠近，合并成一個單獨的大裂紋，最終平板斷裂失效；對于TEC-S5H20和TEC-S10H20試樣，兩個裂紋尖端的擴展方向近乎垂直于加載方向，兩裂紋獨立擴展未發生合并，直至平板斷裂失效。通過計算平板斷裂失效時的Kr值和Lr值，并在失效評定圖上作圖，可發現平板的失效模式為韌性撕裂。

(a)TEC-S5H10試樣(S=5 mm,H=10 mm)

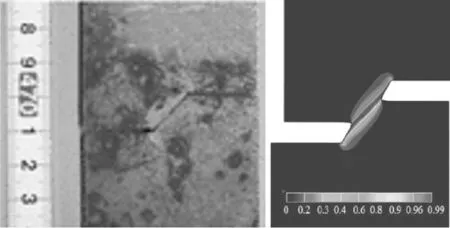
(b)TEC-S10H10試樣(S=10 mm,H=10 mm)

(c)TEC-S5H20試樣(S=5 mm,H=20 mm)

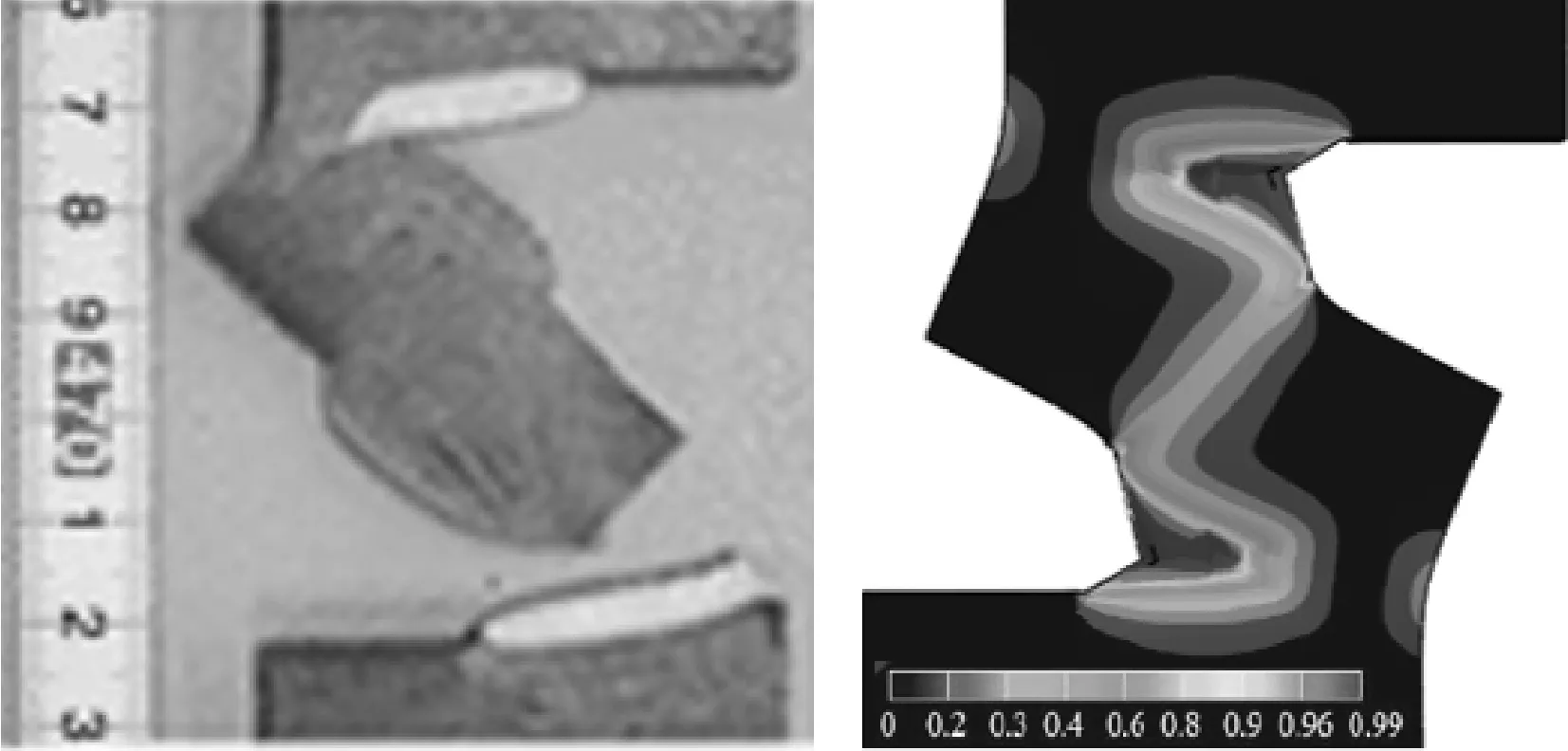
(d)TEC-S10H20試樣(S=10 mm,H=20 mm)圖5 采用非單調斷裂應變軌跡關系時，不同試樣的損傷云圖與斷后試樣照片[6]對比Fig.5 Comparisons between damage nephogram of different specimen using non-monotonic fracture strain locusand photographs of fractured specimen[6]

3.2 斷裂應變軌跡關系對模擬結果的影響

為了驗證不同斷裂應變軌跡關系對多裂紋合并結果的影響，進一步采用單調斷裂應變軌跡關系和修正應力斷裂應變模型對試樣進行模擬，預測的裂紋合并結果如表4所示。圖6示出了TEC-S20H20試樣采用不同斷裂應變軌跡關系時模擬結果與試驗結果對比，可以看出，當采用非單調斷裂應變軌跡關系時，預測結果與試驗結果一致。相反地，由于單調斷裂應變軌跡關系和修正應力斷裂應變模型忽略了低應力三軸度對材料延性的影響，有限元模擬不能準確地再現裂紋合并過程。圖7示出TEC-S20H20試樣在最大載荷時的應力三軸度分布，結果表明兩個裂紋之間的區域處于低應力三軸度水平。因此，如果斷裂應變軌跡關系是單調的，會極大高估該區域的斷裂應變，進而影響對裂紋擴展方向的預測。相同的理由可以解釋TEC-S10H10試樣采用單調斷裂應變軌跡關系不能準確預測裂紋合并過程，因此，采用非單調斷裂應變軌跡關系有限元模擬結果要優于采用單調斷裂應變軌跡關系和修正應力的斷裂應變模型的模擬結果。

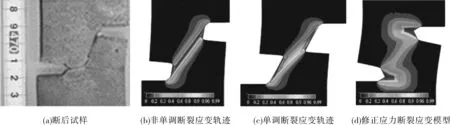
圖6 采用不同斷裂應變軌跡時，TEC-S20H20損傷模擬結果與試驗結果對比

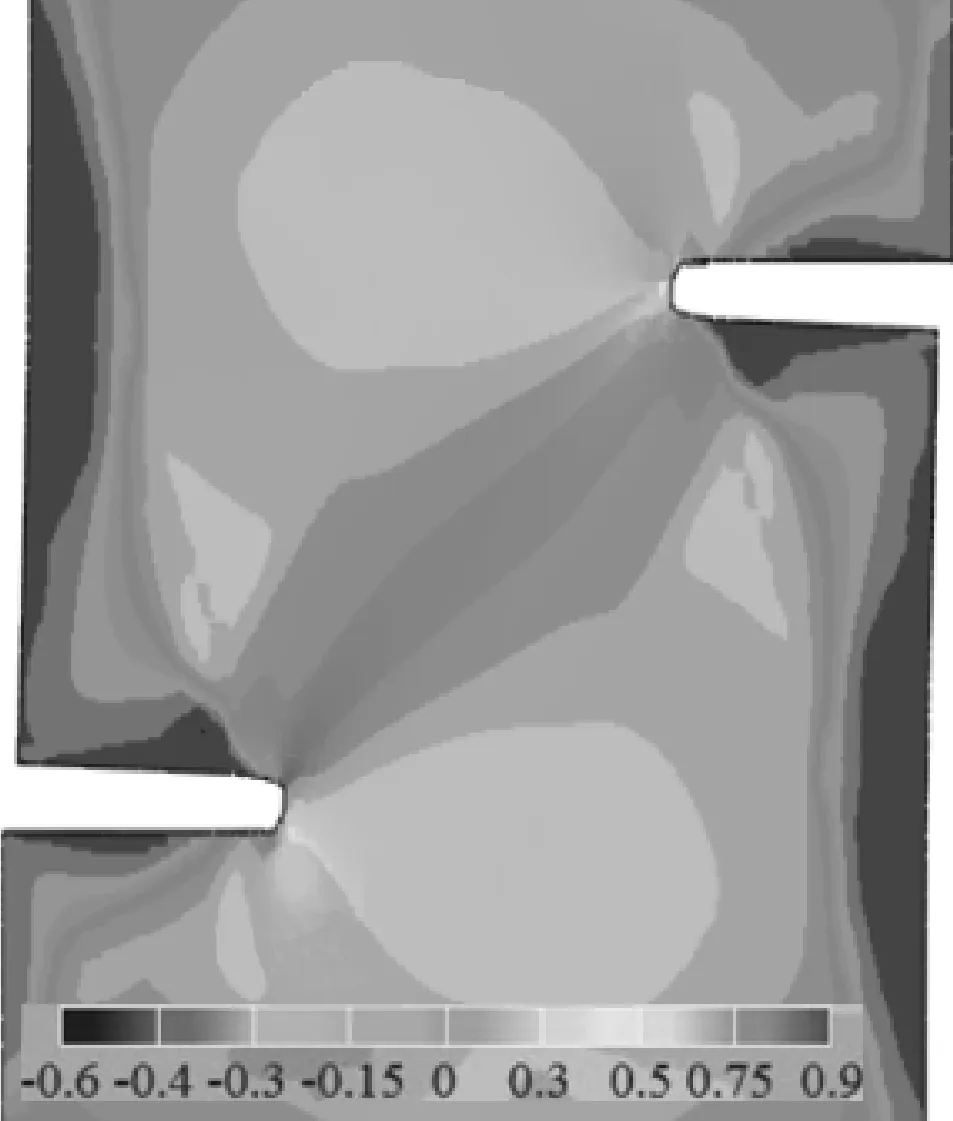
圖7 TEC-S20H20試樣最大載荷時的應力三軸度分布

圖8示出模擬預測的最大載荷與試驗最大載荷的對比，結果表明，采用三種不同的斷裂應變軌跡關系的有限元模擬都可以準確預測最大載荷。圖9比較了采用不同斷裂應變軌跡關系時預測結果的平均絕對誤差，可以發現，采用非單調斷裂應變軌跡關系、單調斷裂應變軌跡關系和修正應力斷裂應變模型的預測最大載荷的平均絕對誤差分別為1.8%，2.7%，2.2%，采用非單調斷裂應變軌跡關系時的平均絕對誤差最小，這說明采用非單調斷裂應變軌跡關系可以相對更加準確地預測最大載荷。

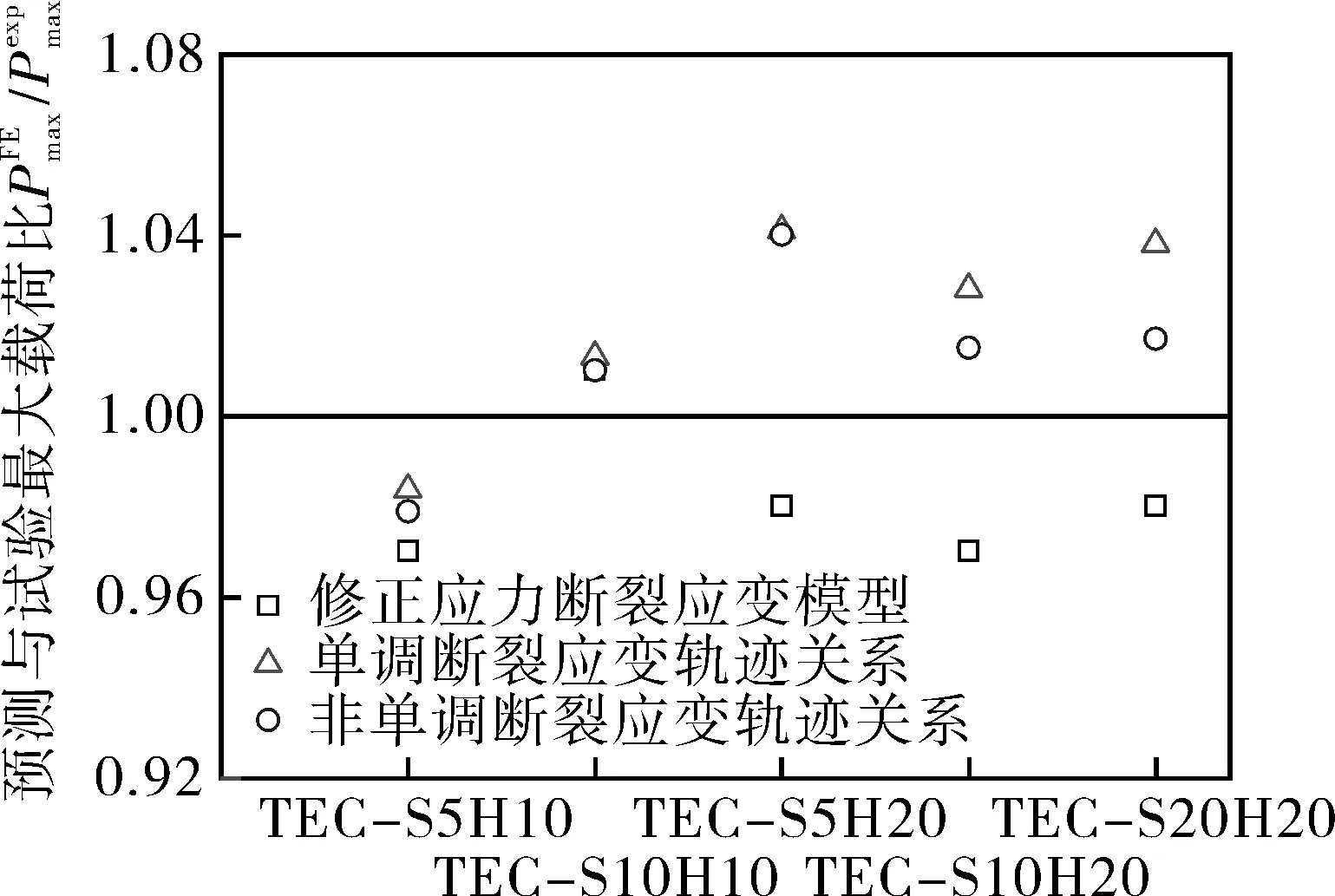
圖8 采用不同斷裂應變軌跡時，預測最大載荷與試驗最大載荷對比Fig.8 Comparison between predicted maximum load andexperimental maximum load using different fracture strain locus

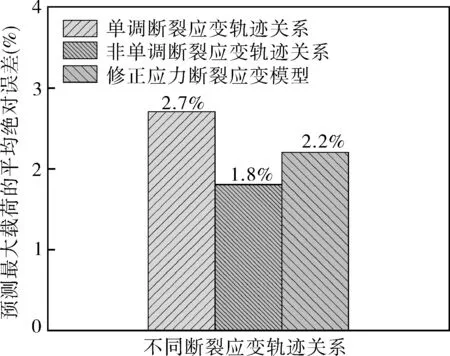
圖9 采用不同斷裂應變軌跡時預測最大載荷的平均絕對誤差Fig.9 Mean absolute error of predicted maximum loadsusing different fracture strain locus

對于TEC-S5H10和TEC-S10H10試樣，分別在有限元模擬結果中提取了試樣中心位置標距為10 mm兩點處的位移變化，得到預測的載荷-位移曲線，圖10示出了預測的載荷-位移曲線與試驗結果的對比。結果表明，相比采用單調斷裂應變軌跡關系和修正應力斷裂應變模型的預測結果，采用非單調斷裂應變軌跡關系模擬時的載荷隨位移變化情況與試驗數據吻合較好，進一步證明了采用非單調斷裂應變軌跡關系預測平板斷裂失效行為的準確性。

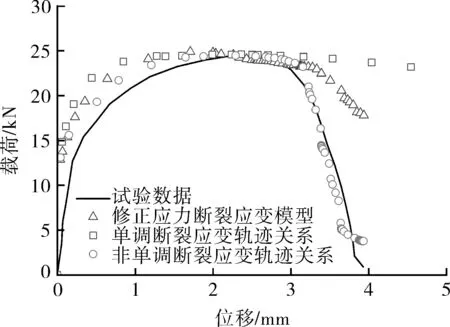
(a)TEC-S5H10試樣(S=5 mm,H=10 mm)

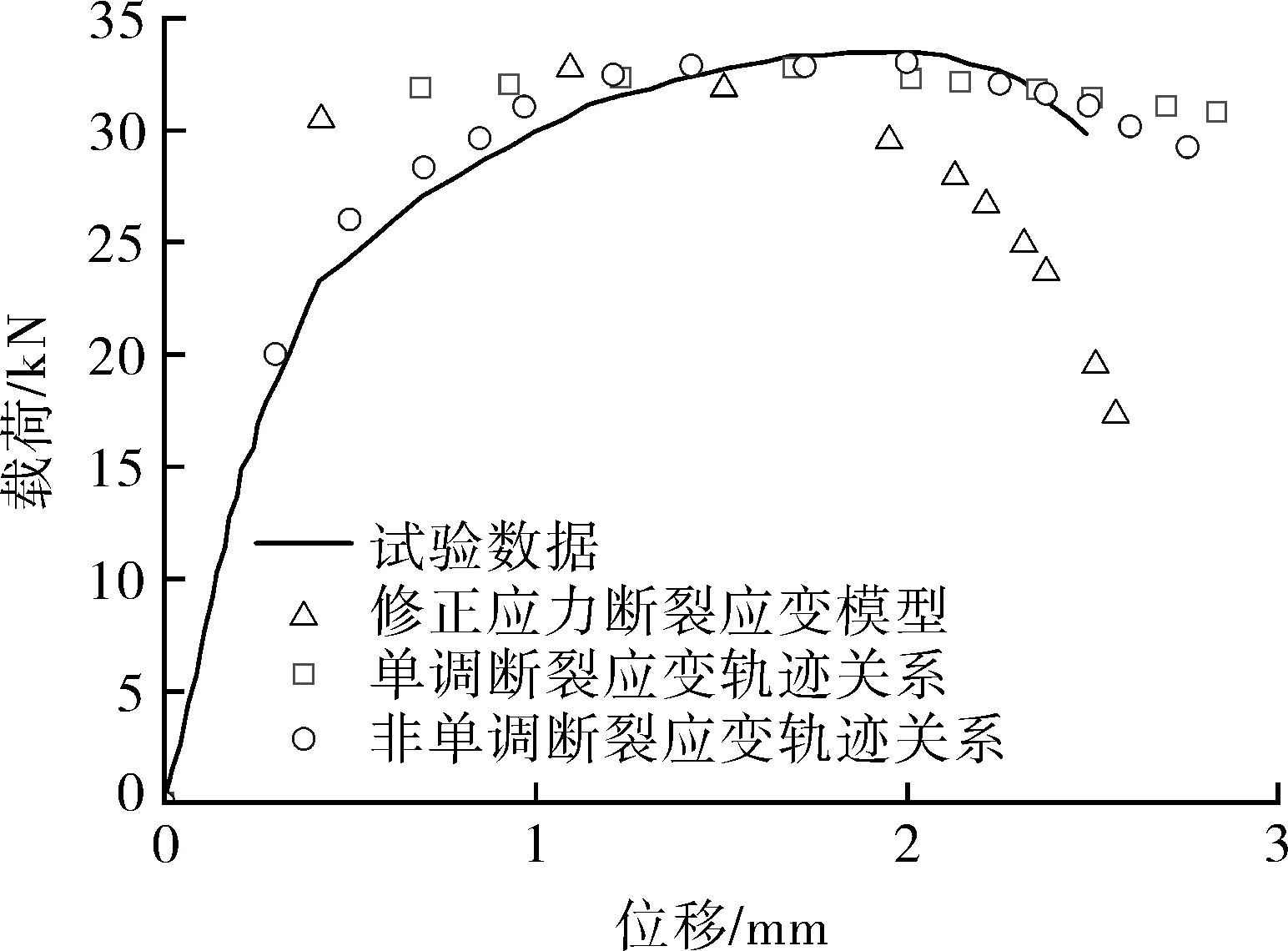
(b)TEC-S10H10試樣(S=10 mm,H=10 mm)圖10 模擬的載荷-位移曲線與試驗載荷-位移曲線對比Fig.10 Comparison between simulated load-displacementcurves and the experimental load-displacement curves

3.3 幾何模型應力狀態假設對預測結果的影響

采用結合非單調斷裂應變軌跡關系的損傷演化模型，并基于不同應力狀態假設條件下的二維模型，對含有邊緣型穿透裂紋平板試樣進行模擬。圖11示出了不同幾何模型預測最大載荷與試驗載荷的對比，可以發現，基于平面應變假設條件下的二維幾何模型會極大地高估最大載荷，其最大誤差為19.3%；而基于平面應力假設條件下的試樣最大載荷則被極大低估了，其最大誤差為8.2%。相比之下，三維模型預測的最大載荷更接近于試驗最大載荷。圖12比較了不同幾何模型下預測的最大載荷的平均絕對誤差，可以看出，三維模型的平均絕對誤差最小，僅為1.8%，進一步說明了采用三維幾何模型比二維幾何模型能更準確地預測平板的最大載荷。

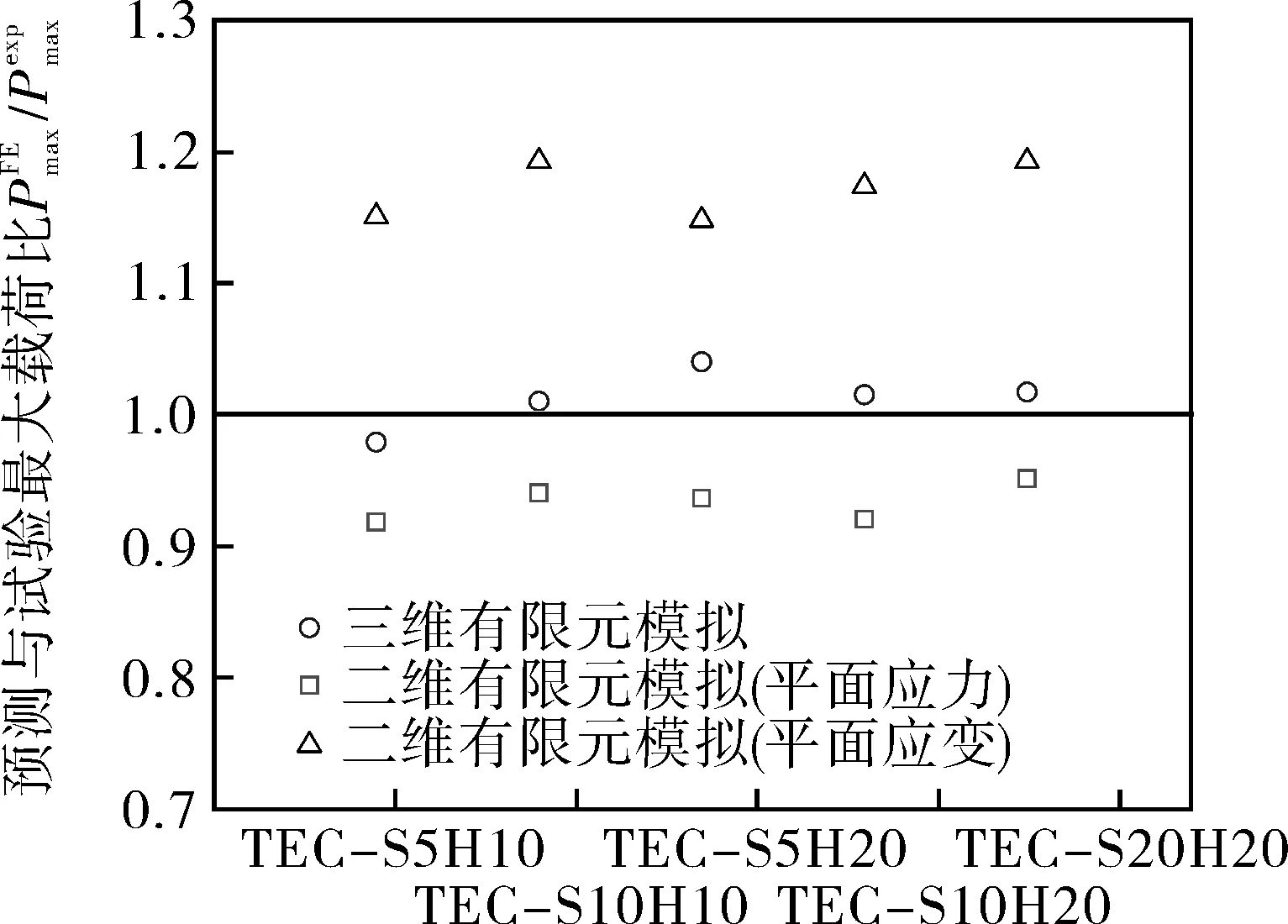
圖11 采用不同幾何模型時預測最大載荷與試驗最大載荷對比Fig.11 Comparison between predicted maximum load andexperimental maximum load using different geometric models

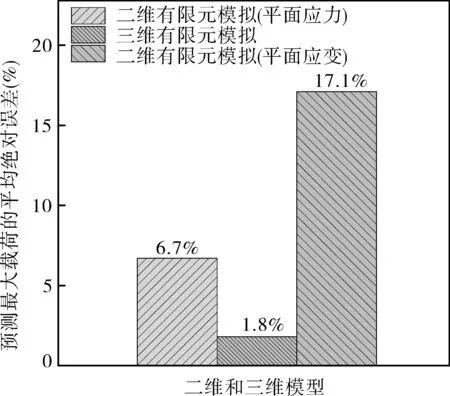
圖12 采用不同幾何模型時預測最大載荷的平均絕對誤差Fig.12 Mean absolute error of predicted maximum loadsusing different geometric models

與此同時，采用不同幾何模型時裂紋合并預測結果如表5所示。可以看出，基于平面應力假設條件下的二維幾何模型無法準確預測TEC-S20H20試樣的裂紋合并過程，而基于平面應變假設條件時則無法準確預測TEC-S10H10和TEC-S20H20試樣的裂紋合并過程。因此，采用三維模型的預測結果比基于平面應力和平面應變狀態假設預測結果均更加準確。

表5 采用非單調斷裂應變軌跡時，二維和三維模型有限元預測裂紋合并結果與試驗結果對比Tab.5 Comparison between crack coalescence results predicted by two-dimensional model and three-dimensional model using non-monotonic fracture strain locus and the experimental results

4 結論

(1)相比于合乎使用規范中的多裂紋共線與合并準則，采用本文建立的延性損傷分析方法可以更加準確地判斷邊緣型穿透多裂紋的合并情況。

(2)采用非單調斷裂應變軌跡關系時的預測結果要優于采用單調斷裂應變軌跡關系和修正應力斷裂應變模型時的預測結果，說明不同斷裂應變軌跡關系對有限元預測結果具有顯著的影響。

(3)采用三維幾何模型預測的最大載荷和多裂紋合并情況比基于平面應力或平面應變狀態假設預測的結果更加準確。