基于遺傳算法優化的電弧增材再制造焊道尺寸預測模型

倪永謙 王猛 杜心偉 劉仁培 魏艷紅

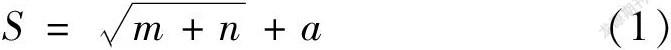
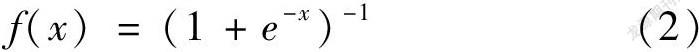
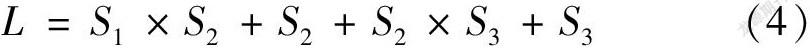
摘要：電弧增材再制造過程中，成形件通過層層累積的方式進行制造。每道焊縫的幾何尺寸對構件的成形精度有著重要的影響，是分層切片和路徑規劃的重要依據之一。為了研究焊接工藝參數與焊道尺寸之間的關系，文中采用正交試驗法進行單道焊縫成形試驗，建立了基于遺傳算法的神經網絡模型，可以預測不同焊接工藝參數（焊接電流、焊接速度、送絲速度）下單道成形的熔寬和余高。結果表明，焊縫寬度的預測平均誤差為2.05%，焊縫高度的預測平均誤差為5.09%，該模型實現了對焊道尺寸的較高精度的預測。結合多層多道試驗對模型進行了驗證，結果顯示成形件成形良好，成形精度較高。文中建立的神經網絡模型為電弧增材制造過程的工藝優化提供了依據。

關鍵詞：電弧增材再制造;焊道尺寸;神經網絡;遺傳算法

中圖分類號：TG 444

Abstract：In the arc additive remanufacturing process， the formed parts are manufactured by layer-by-layer accumulation. The geometric size of each weld has an important influence on the forming accuracy of components， and is one of the important bases for layered slicing and path planning. In order to study the relationship between welding process parameters and weld bead size， orthogonal experiments were used to conduct single-pass weld forming experiments in this paper， and a neural network model based on genetic algorithms was established， which could predict weld width and reinforcement of single pass forming under different welding parameters such as welding current， welding speed and wire feeding speed. The results showed that the average prediction error of weld width was 2.05%， and the average prediction error of reinforcement was 5.09%. The model achieved a high-precision prediction of the weld pass size. The model was verified by multi-layer and multi-pass experiments， and the results showed that the formed parts were well formed and the forming accuracy was high. The neural network model established in this paper provided a basis for the process optimization of the arc additive manufacturing process.

Key words：arc additive remanufacturing;weld pass size;neural networks;genetic algorithm

0 前言

電弧增材再制造技術是基于電弧增材制造技術，通過層層堆積的制造方式，實現零部件損傷部位的尺寸恢復和零部件性能恢復或提升的先進制造技術，具有制造成本低、修復效率高、零件性能好、材料利用率高等優點[1-2]。電弧增材再制造技術在航空航天、能源化工、軌道交通等高端技術裝備領域具有廣闊的應用前景。

成形件精度較低是制約電弧增材再制造技術發展的重要因素，保證成形效率的同時提高成形件精度是當下主要研究方向之一[3-5]。單道焊縫成形尺寸精度的控制對于增材再制造構件的成型精度具有重要影響，國內外學者對焊接參數和焊縫尺寸之間的模型關系也做了大量研究工作，Tao等人[6]開發了一種二階回歸模型來定量估計工藝變量對焊道幾何形狀的影響;Xiong等人[7]比較了人工神經網絡（ANN）和二階回歸模型在4個焊接工藝變量下預測焊縫高度和寬度的準確性;Nagesh等人[8]建立了一個反向傳播神經網絡（BPNN）模型，該模型實現了輸入因素（送絲速度、電弧功率、電弧電壓、焊接電流、電弧長度和焊接速度）和輸出因素（焊道高度、焊道寬度、焊道深度和焊道面積）之間的較高精度預測。

目前，已經證明人工神經網絡在預測焊道幾何尺寸方面有較高的預測精度和較強的泛用性[9]。然而，神經網絡模型的結構及初始權值和閾值的選擇會對網絡訓練精度產生較大影響，易出現局部最優解情況，降低模型精度。因此，文中采用遺傳算法優化神經網絡的方法對焊接工藝參數和焊道尺寸進行建模，實現依據焊接工藝參數對焊道尺寸的預測，提高模型的可靠性。

1 試驗設備及方法

電弧增材再制造成形系統系統由GP12_AR1440工業機器人、機器人控制柜、焊接電源、送絲機構、冷卻水箱、焊槍及工作臺等部件組成。試驗基板為Q235B鋼板，尺寸為300 mm×200 mm×20 mm。焊絲為牌號RMD535模具修復專用藥芯焊絲，直徑1.6 mm，保護氣體成分為80%Ar + 20%CO2，流量為15 L/min。

試驗開始前，對基板表面進行機械打磨去除表面氧化層等雜質，隨后用酒精清潔基板表面并風干處理對基板表面進行機械打磨，并用酒精清洗干凈，然后將基板固定在工作臺上，并設定好機器人焊槍運動軌跡及焊接工藝參數，進行試驗。

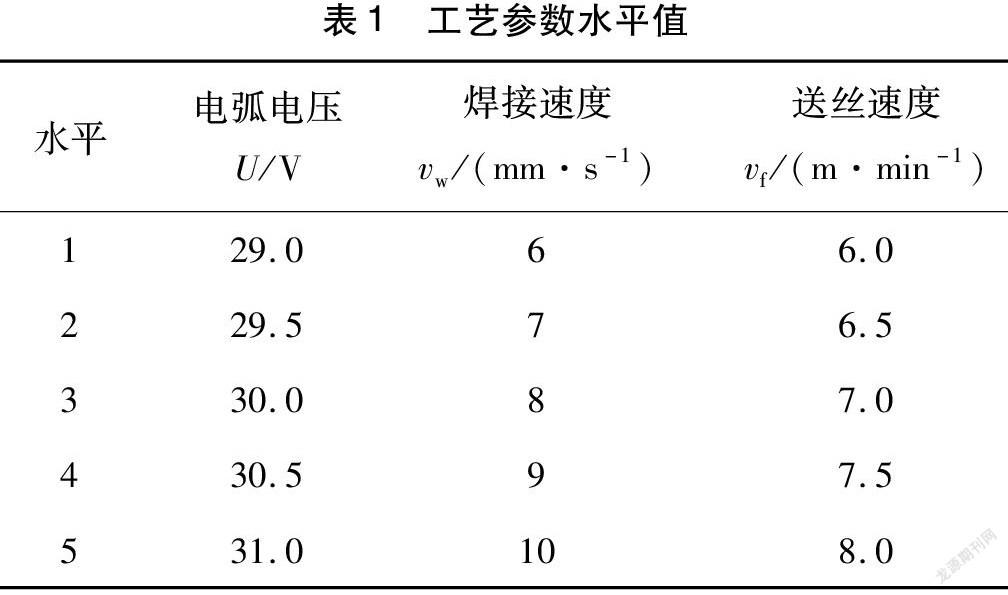
電弧增材再制造成形過程的主要影響因素較多，包括電弧電壓、焊接電流、送絲速度、焊接速度、焊絲伸出長度及保護氣體流量等，各個因素之間存在高度的非線性耦合作用。其中，電弧電壓、焊接電流、送絲速度和焊接速度對焊道的熔寬和余高影響較大，因此文中選取電弧電壓、送絲速度和焊接速度3個焊接工藝參數為因素，在每個因素中選取5個水平值，選用L25（53）的正交試驗設計方案，見表1，獲得不同試驗方案下的焊縫幾何尺寸特征。

圖1為單道成形外觀形貌，表面呈現魚鱗狀，焊道寬高變化均較小。

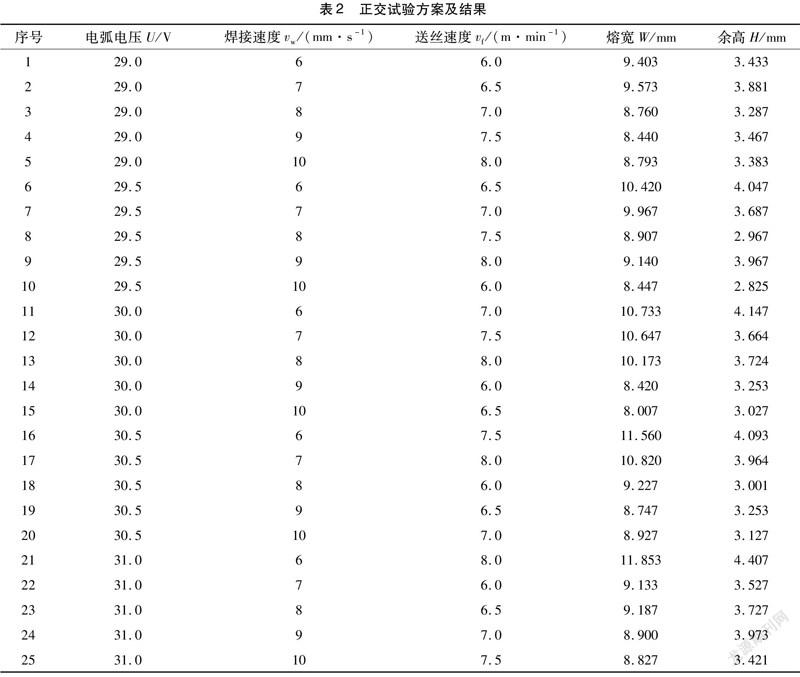
試驗結束后，對焊道熔寬W和余高H進行測量，如圖2所示。用游標卡尺測量不同的焊接工藝參數對應的焊道高度與寬度的數值。

為減小測量誤差以保證試驗結果的可靠性和準確性，在焊道平整光滑處進行測量，每組數據均測量3次并取平均值。試驗結果見表2。

2 焊道尺寸預測模型建立

2.1 焊道尺寸BP神經網絡的構建

為提高焊道尺寸預測精度，文中引入3層結構的神經元網絡模型，神經網絡模型輸入層3個節點分別為電弧電壓、焊接速度、送絲速度，輸入層神經元個數為3;輸出層節點為焊道熔寬和余高，輸出層神經元個數為2;隱藏層神經元個數參考經驗式（1）所示：

式中：S為隱藏層神經元個數;m為輸入層神經元個數;n為輸出層神經元個數;a為1～10之間的常數。

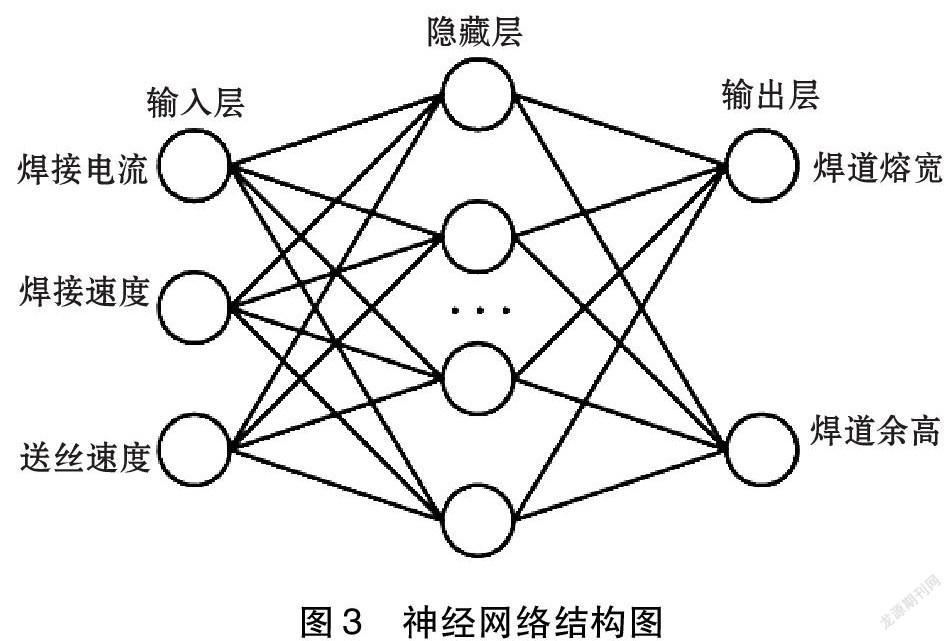
通過多次試驗，比較不同隱藏層節點時的MSE（均方偏差特性函數），最終確定隱藏層層數為10層。文中創建的 BP 神經網絡模型結構是3-10-2型，所建立的神經網絡結構圖如圖3所示。

神經網絡每層之間存在連接權值，且各層均具有閾值和激活函數，利用激活函數正向傳遞輸入值，求得輸出值。BP神經網絡最常用的激活函數有Sigmoid，Tanh和Relu，文中選擇Sigmoid作為激活函數，如式（2）所示：

使用Mapminmax函數完成數據的歸一化處理，確保其不超過[-1，1]的取值范圍，最后對網絡輸出的數據展開反歸一化操作，從而獲取真實的輸出值。Mapminmax函數的具體公式如下：

式中：x為樣本數據;xmin為樣本數據中最小值;xmax樣本數據中最大值;y為對x進行歸一化后得到的數據;ymin和ymax為歸化參數，默認值為-1和1。

根據網絡調參經驗確定網絡訓練函數為Levenberg-Marquardt算法，訓練函數為trainlm，網絡學習速率取0.01，最大訓練次數為1 000次。

2.2 基于遺傳算法的神經網絡模型

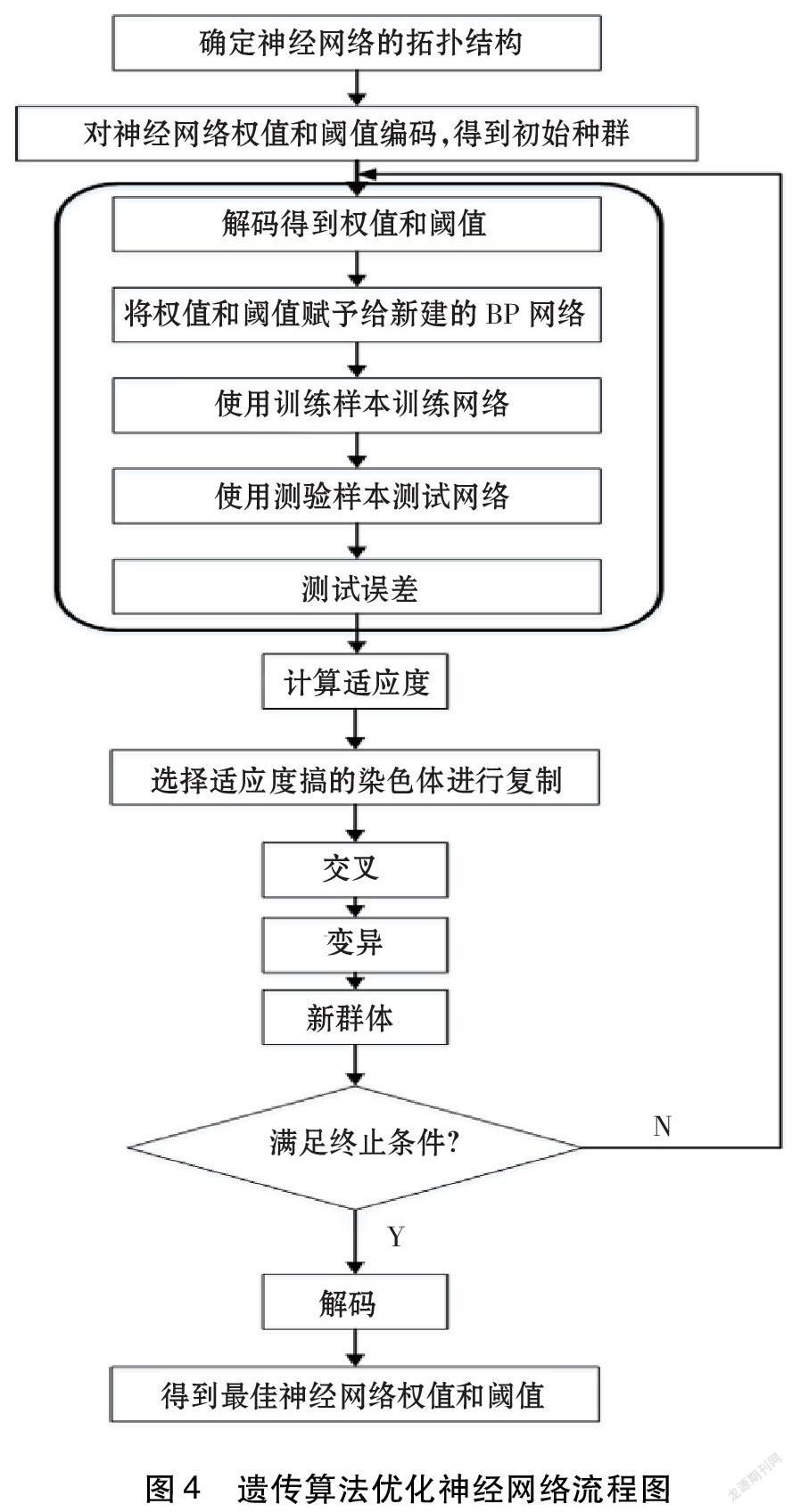
BP神經網絡的初始權值和閾值具有隨機性，因此容易得到局部最優解而非全局最優解。文中采用遺傳算法 （Genetic algorithm，GA）來優化訓練BP神經網絡的連接權值和閾值，利用遺傳算法全局搜索的特性，提高神經網絡的泛化性能，優化BP神經網絡權值初始化的隨機性，提高模型預測的精度[10-11]。遺傳算法優化神經網絡模型具體包括種群初始化、選擇適應度函數、選擇算子、交叉算子和變異算子，具體結構示意如圖4所示。

2.2.1 初始化種群

初始化種群主要包括確定編碼方式、種群規模及最大迭代次數。文中的個體編碼采用二進制編碼，每個個體均為一個二進制串，染色體的長度為：

式中：S1為輸入層節點數;S2為隱含層節點數;S3為輸出層節點數。文中創建的 BP 神經網絡模型結構是3-10-2型，計算得到染色體長度為62。設定初始種群規模M=60，最大迭代次數G=200。

2.2.2 適應度函數

為使BP神經網絡在預測時，預測值與期望值的殘差盡可能小，選擇預測樣本與期望值的誤差矩陣的二范數作為目標函數的輸出。

2.2.3 遺傳算子

選擇算子是從父代群體中選擇個體遺傳到下一代群體中的方法，文中采用輪盤賭法選擇算子，設定代溝值GGAP=0.95;交叉算子操作是指將2個不同個體按照某種方式相互交換而形成新個體的方法，文中選用單點交叉算子，設定交叉概率值Px=0.7;變異算子操作是以一定概率產生變異基因數，用隨機方法選出發生變異的基因的方法，文中選取是基本位變異方式，設定變異概率值Pm=0.01。

遺傳算法的優化過程是首先對初始化種群，選擇部分優秀個體進入下一代種群，然后重復交叉操作和變異操作以產生新個體，如此循環即可保證神經網絡得到最優解或達到設定的最大迭代次數。

2.3 遺傳算法優化神經網絡模型預測結果

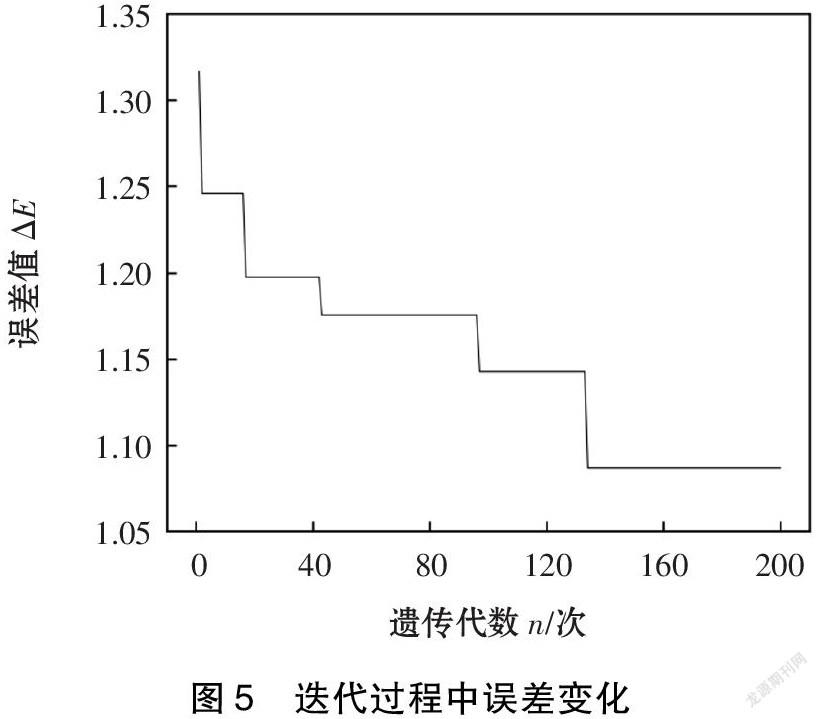
為驗證所提出的遺傳算法優化神經網絡焊道尺寸預測模型的性能，在迭代過程中跟蹤誤差值，如圖5所示。誤差值在迭代過程中隨迭代次數遞增而不斷減小，這表明個體適應度在選擇、交叉和變異過程中不斷提高，最終個體逐漸接近目標值，遺傳算法優化神經網絡模型相比于神經網絡模型具有更高的預測精度。

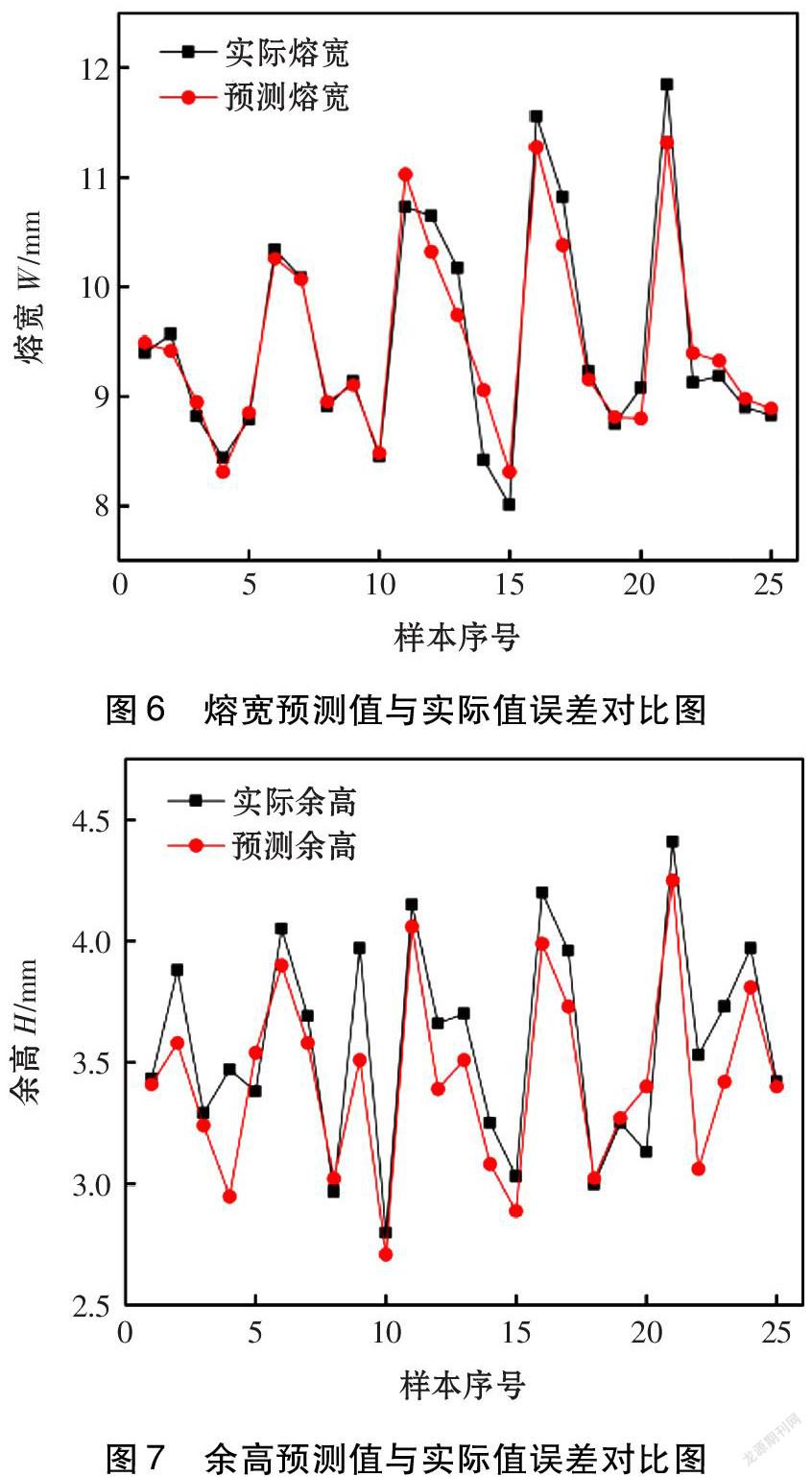
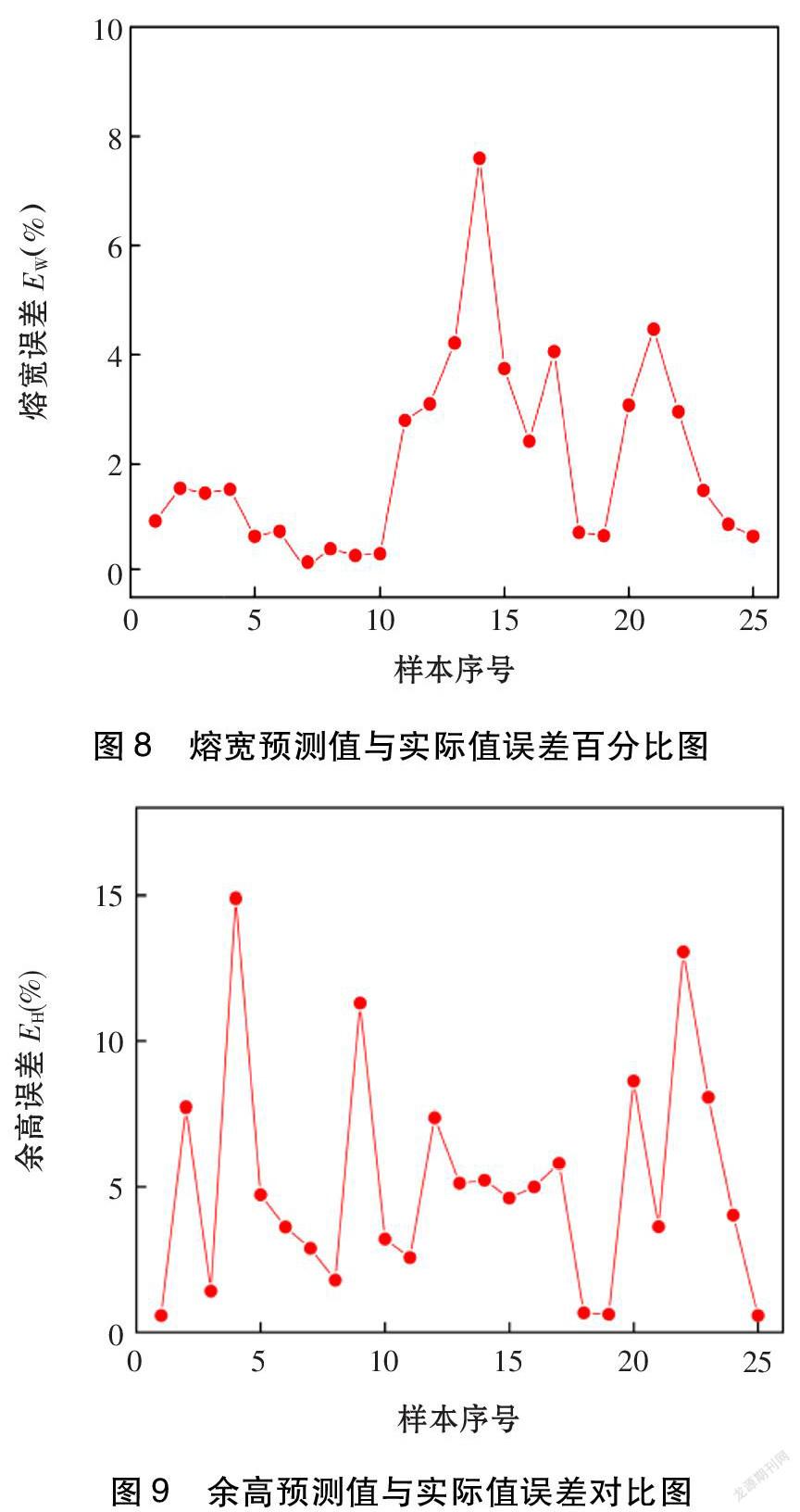
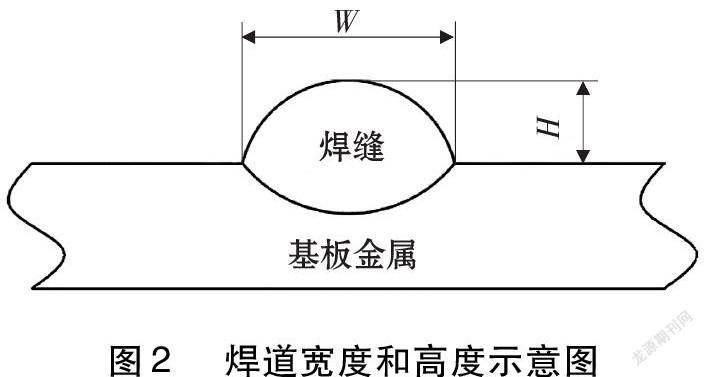
通過建立的遺傳算法優化神經網絡模型進行預測，并將預測結果與試驗結果進行比較，從而得到預測樣本輸出誤差值如圖6～圖7所示，焊道熔寬和余高的預測值與實際值相差較小。其中，如圖8所示，預測熔寬和實際熔寬的誤差平均值為2.05%;如圖9所示，預測余高和實際余高的誤差平均值為5.09%。表明采用該模型進行焊道尺寸模型預測具有較高的精度和可靠性。

3 多層多道焊驗證試驗

3.1 試驗流程

為驗證遺傳算法優化神經網絡模型的精度，采取多道多層試驗的方式進行驗證。首先通過三維建模軟件繪制3D模型，對模型進行等厚切片處理，然后依據3D模型尺寸并結合神經網絡模型預測出焊道成形尺寸，進行層內及層間軌跡規劃，最后設定機器人焊接工藝參數制造成形件。

3.2 多層多道成形試驗

長方體預制件模型寬度為100 mm、長度為200 mm，高度為30 mm。根據所建立的GA-BP神經網絡模型選取合適的焊接工藝參數，最終確定電弧電壓為30.5 V、焊接速度8 mm/s，送絲速度為6.5 m/min。為改善焊縫側表面的塌陷現象，層內路徑采用輪廓偏置結合Zigzag的路徑規劃方式，即先焊外輪廓包絡圈，再以Ziagzag的方式填充內部區域;為提高成形件尺寸精度，層間路徑采用垂直交錯堆積的方式，共堆積8層，層間冷卻時間5 min。圖10為多層多道試驗實物圖。成形件平均尺寸為寬度100.74 mm、長度201.32 mm、高度29.52 mm。成形件表面成形質量總體良好，表面層中間區域最高高度為29.87 mm，最低高度為29.35 mm，誤差小于1 mm。但因為熱積累和加工誤差仍導致成形件出現側面塌陷的現象，降低了成形件尺寸精度。

4 結論

（1）文中結合正交試驗電弧增材制造試驗數據，選取電弧增材再制造影響焊縫尺寸的焊接工藝參數，建立以電弧電壓、焊接電流、送絲速度為輸入量，以焊縫的熔寬和余高為輸出量的BP神經網絡焊縫尺寸預測模型。

（2）采用遺傳算法對BP神經網絡的初始權值和閾值進行優化，尋求全局最優解。結果表明，經遺傳算法優化的BP神經網絡模型的預測誤差較小，網絡穩定性能較好，提高了模型的泛化能力和預測精度。建立預測模型可以在電弧增材再制造一定的焊接工藝參數范圍內的實現焊縫尺寸的較精準預測。

（3）結合多層多道試驗對模型進行驗證，結果顯示成形件成形良好，成形精度較高。文中建立的遺傳算法優化神經網絡模型在實際生產過程中對于選取合適的焊接工藝參數具有借鑒意義。

參考文獻

[1] Mughal M P， Fawad H， Mufti R A. Three-dimensional finite-element modelling of deformation in weld-based rapid prototyping [J]. ARCHIVE Proceedings of the Institution of Mechanical Engineers， Part C：Journal of Mechanical Engineering Science 2006， 220（6）：875-885.

[2] 蔡笑宇， 董博倫， 殷憲錸， 等. 預熱溫度對GTA增材制造鈦鋁合金組織及性能的影響 [J]. 焊接學報， 2021， 42（10）：14-21.

[3] 董曼淑， 朱晗， 張曉超， 等. 礦用鏈輪鏈窩電弧增材制造路徑規劃[J]. 焊接， 2021（1）：51-55.

[4] Zhao Pengkang， Fang Kui， Tang Cheng， et al. Effect of interlayer cooling time on the temperature field of 5356-TIG wire arc additive manufacturing [J]. China Welding， 2021， 30（2）：17-24.

[5] 李超， 朱勝， 沈燦鐸， 等. 焊接快速成形技術的研究現狀與發展趨勢[J]. 中國表面工程， 2009， 22（3）：7-12， 20.

[6] Tao Y， Xiong J， Hui C， et al. Modeling of weld bead geometry for rapid manufacturing by robotic GMAW [J]. International Journal of Modern Physics B， 2015， 29（10-11）：1-7.

[7] Xiong J， Zhang G， Hu J， et al.Bead geometry prediction for robotic GMAW-based rapid manufacturing through a neural network and a second-order regression analysis [J]. Journal of Intelligent Manufacturing， 2014， 25（1）：157-163.

[8] Nagesh D S， Datta G L. Prediction of weld bead geometry and penetration in shielded metal-arc welding using artificial neural networks [J]. Journal of Materials Processing Technology， 2002， 123（2）：303-312.

[9] Li R， Dong M， Gao H. Prediction of bead geometry with changing welding speed using artificial neural network [J]. Materials， 2021， 14（6）：1-9.

[10] Kim I S， Son J S， Park C E， et al. A study on prediction of bead height in robotic arc welding using a neural network [J]. Journal of Materials Processing Technology， 2002， 130-131：229-234.

[11] Kim I S， Son J S， Park C E， et al. An investigation into an intelligent system for predicting bead geometry in GMA welding process [J]. Journal of Materials Processing Technology， 2005， 159（1）：113-118.