基于弦振動的混沌實驗裝置研制

丁格曼 徐頌華 林墁烔 葉文超 劉家豪 謝翠婷

(華南師范大學物理與電信工程學院 廣東 廣州 510006)

混沌現象起源于非線性系統對初始條件的敏感依賴性，是由確定性方程描述的簡單系統出現極為復雜的貌似隨機的無規則運動現象.本裝置從混沌動力學理論出發，制作弦振動混沌實驗裝置，利用NI myDAQ數據采集卡和虛擬儀器處理系統，可直觀地觀察和研究弦線振動由混沌運動向周期有序運動相互轉換的過程，并通過Matlab對實驗結果進行仿真驗證.

1 實驗原理

1.1 振動源帶動弦線實驗中的混沌現象及理論分析

在弦振動實驗弦線前加上振動源，當弦線和振動源的連接點調整到接近駐波波節處時，振動系統會形成混沌現象.這種不穩定振蕩正是振動源振動端的非線性振動所引起的，此時振動源振動端處于不規則周期運動狀態或混沌狀態，進而把整個振動系統帶入不穩定振動狀態[1].

如圖1所示，選定弦線固定端點(反射處)為坐標原點x=0，當有阻尼力時，沿x軸反向(即遠離振動源方向)駐波振幅不斷衰減，距離越大衰減越快.實驗中弦線的阻尼小，因此采用弦線作為實驗材料，則形成的弦線駐波方程為[2]

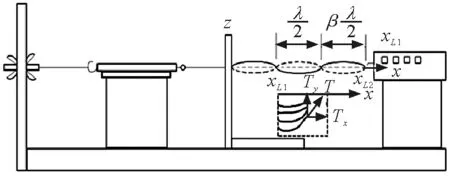
圖1 實驗振動裝置原理圖

(1)

其中弦線長度

(2)

針對振片振動情況進行研究，本實驗中振片受振動儀驅動力F驅、振片恢復力F恢和弦線張力T.在上述力的共同作用下進行運動，可得振片的運動狀態為

(3)

其中m為振片振動時的有效質量；F恢=-ky；F驅=Focosωt；Ty為弦線張力T的橫向分量，即Ty=Tsinθ，θ是振動源與弦線連接處弦線的切線角，如圖2所示.

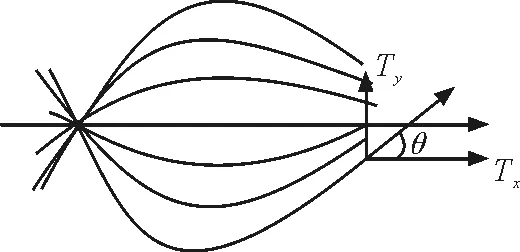
圖2 弦線張力分解圖

根據圖2分析可知，xL處弦線張力的分量Ty對振片振動有作用，而Tx分量并沒有作用，因此式(3)中僅含有Ty.切線角θ可通過弦線振動方程來求解，利用式(3)進行分析可知θ滿足[2]

(4)

故式(3)可改寫為

(5)

其中，y為振片縱向位移；k是振片恢復系數；γ為主要由自身阻尼和弦線張力垂直分量決定的阻尼系數；T是弦線張力；ω為振片振動圓頻率.上式就是能產生混沌運動的非線性運動方程.

1.2 駐波實驗非線性系統運動的數值分析及仿真

在LabVIEW中內嵌數值模擬部分，即可將實驗結果與理論模型進行對比.為了簡化計算又不失規律性，將式(5)轉化成了無量綱標準型[3]

(6)

其中做了變化，令

當系統振動起來后，振動儀的驅動力頻率與振動系統的固有頻率相同，因此式(6)中取a=1.另外根據實驗的具體情況，不失一般性地取電磁鐵驅動力因子d=0.8,弦線張力因子c=1.0，p=0.637.選擇初始條件(X0，Y0)改變β，對式(6)進行數值模擬研究，從而可得到相圖和波形時域圖，依此來判斷混沌現象的發生[4].

根據系統參數a,b,c,d,p,q和初始條件(X0，Y0)的不同情況，利用Matlab對式(6)進行數值模擬研究，得到振動系統的相圖和時域圖，由此判斷系統的振動狀態.

根據實驗的具體情況，不失一般性地取(b,c,d)=(0.3,1.0,0.5),對β在(0，1)范圍內，不同數值進行數值模擬(X0，Y0)=(0.01，0.05)，得到相圖和時域圖如圖3所示.結果表明：

(1)β處在(0.22,0.77)范圍時，系統振動接近穩定狀態；β處在(0.18,0.21)或(0.78,0.81)范圍時，系統振動接近混沌狀態.

(2)系統處于穩定狀態時，時域圖接近于正弦波，相圖呈現出單個圓形的形狀.

(3)系統處于混沌狀態時，時域圖呈現表面不規律，實際有規律可循的波形，相圖出現帶“雙吸引子”的雙圓形狀.

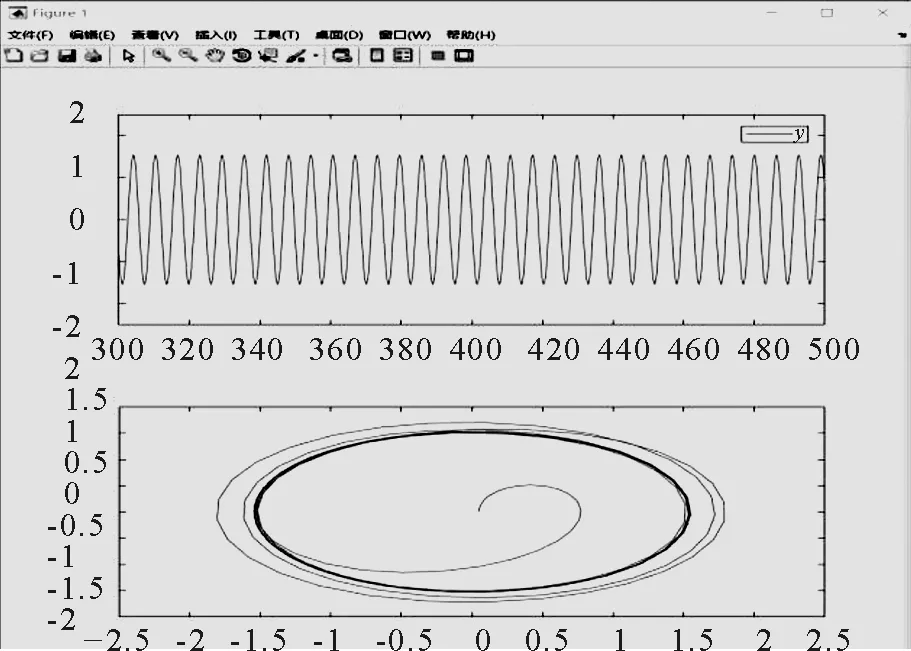
(a) β=0.4時，系統時域圖與相圖

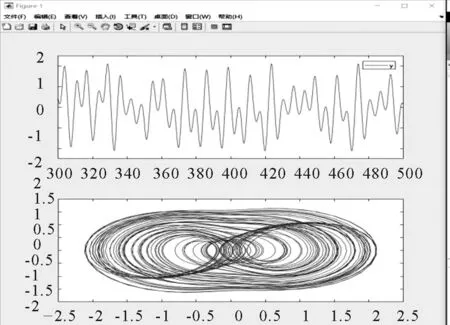
(b) β=0.2時，系統時域圖與相圖

2 混沌實驗裝置設計

混沌實驗裝置主要包括非線性振動平臺、電子裝置與電路系統、數據采集處理系統3部分.

2.1 非線性振動平臺

如圖4所示，非線性振動平臺主要包括振動源,金屬薄片,弦線,駐波顯示屏,彈簧測力計,電渦流傳感器,尺子等.FD-SWE-Ⅱ弦線上駐波實驗儀提供可調節式振源.在振動儀前端延伸固定一個具有較好彈性和小阻尼力的薄金屬振片，在金屬薄片的一側設置一個電渦流傳感器探頭，在振片內部產生電渦流，完成振幅非接觸測量的電信號實時轉換.薄片的另一端連接弦線穿過一個駐波顯示屏(中間帶有一小孔的平面板)，可控制機械波的反射位置并對駐波波節的位置進行測量.穿過小孔再連接一個彈簧測力計，彈簧測力計固定一個螺旋管穿過木板用螺絲固定，能方便控制弦線張力的大小和連續變化.當條件滿足混沌振動時，振片與弦線連接處就會進入混沌振動，從而實現直觀和定量測量.

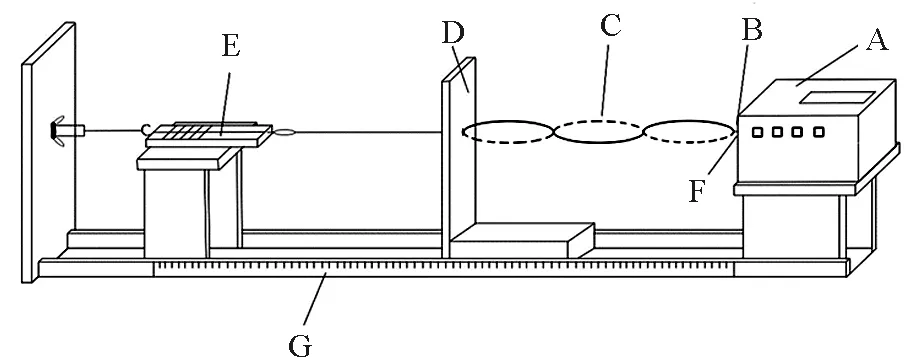
A-振動源;B-金屬薄片;C-弦線;D-駐波顯示屏;E-彈簧測力計;F-電渦流傳感器;G-尺子

圖4 非線性振動平臺實驗裝置圖

2.2 電子裝置和電路系統

裝置的電子電路部分包括直流穩壓電源、電渦

流傳感器、NI myDAQ數據采集卡等.直流穩壓電源負責輸送-24 V電壓供數據采集器使用.弦線振幅的變化由振動源前端金屬振片反映，隨后將轉換成的電信號輸出到數據采集系統中.采集的信號數據經過A/D轉換，再送入計算機進行處理.具體實現過程為：

(1)將電渦流傳感器靠近振動中的銅線.

(2)電渦流傳感器感應到銅線振動后，輸出電信號給數據采集器電路.

(3)數據采集器將電信號經過處理后產生模擬信號，傳遞到LabVIEW數據采集卡NI myDAQ中進行處理.

(4)NI myDAQ數據采集卡將模擬信號轉化為數字信號，經過放大濾波后傳輸到計算機.

2.3 數據采集處理系統

利用LabVIEW軟件平臺，開發數據采集與處理的虛擬儀器，在此虛擬儀器中完成對實驗參數的輸入、實驗數據采集、實驗數據處理、實驗結果實時展示等功能.其主要程序設計框圖如圖5所示.

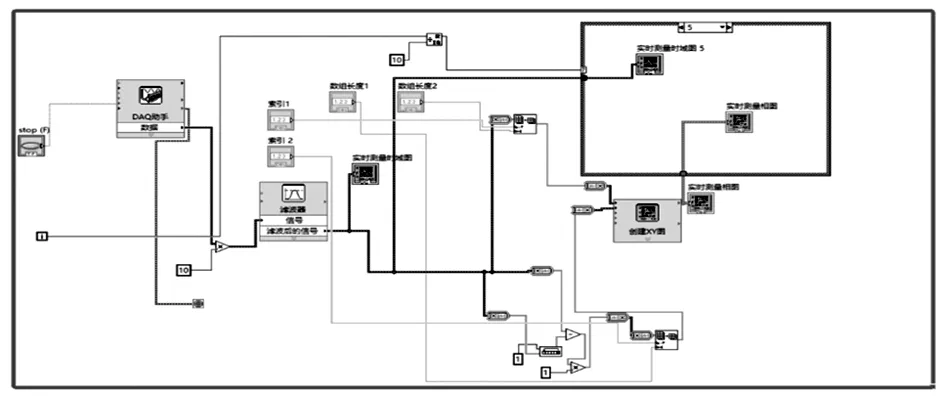
圖5 LabVIEW程序設計框圖

3 實驗觀察及數據記錄處理

3.1 實驗操作

實驗前，先調節駐波振動上弦線位置，使其與實驗平臺保持水平，調節彈簧測力計示數以改變弦線張力，接通駐波振動儀；再打開電子裝置控制開關，此時輸出端與數據采集卡端口連接，數據采集卡另一端口接地，USB端口與電腦連接，隨后啟動LabVIEW軟件相關程序及MALATB仿真程序，輸入相關參數后即可開始實驗[5].

以固定頻率改變拉力為例，實驗操作主要為：

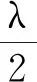
(2)繼續微調駐波屏位置，觀察此時顯示弦線狀態的相圖和時域圖,當相圖出現帶“吸引子”雙圓時，記錄此時振動狀態及駐波顯示屏的位置L.

(3)繼續移動駐波顯示屏位置，當弦線連接端處于波腹位置附近時，觀察時域圖與相圖，當相圖出現單圓時，記錄此時振動狀態及駐波顯示屏的位置L′.

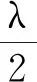
(5)改變拉力大小T，重復以上步驟.

固定拉力大小T不變，改變頻率，觀察相應時域圖與相圖，方法類似故不在此詳述.

3.2 實驗數據記錄

通過上述操作，即固定頻率改變拉力，數據記錄如表1所示.

表1 固定頻率f,改變拉力T實驗數據記錄表

3.3 實驗結果與觀察

實驗過程中，虛擬儀器界面可實時顯示駐波顯示振片處的振動狀態時域圖及相圖，其中固定頻率改變拉力過程中，可觀察隨著β值的改變，弦振動狀態從混沌狀態到穩定狀態的改變過程，如圖6所示.

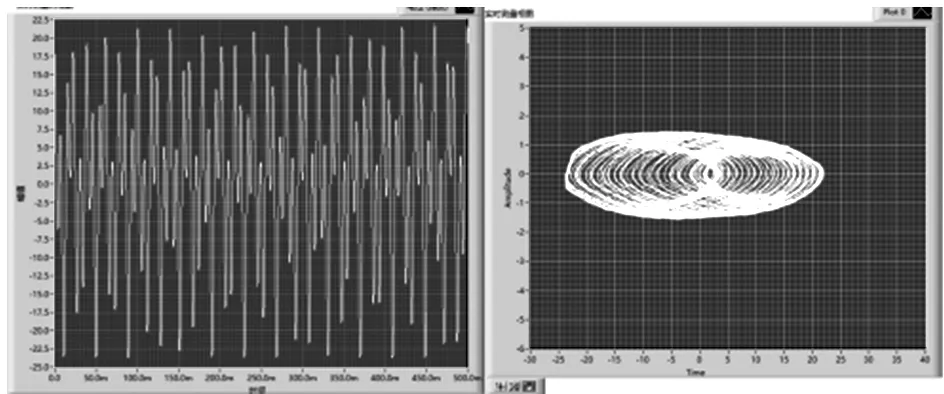
(a) f=128 Hz,T=1.20 N,β=0.20,時域圖及相圖

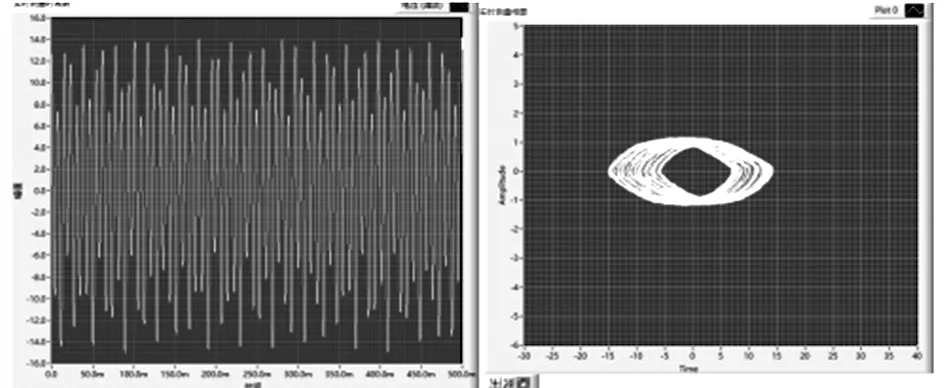
(b) f=128 Hz,T=1.20 N,β=0.56,時域圖及相圖

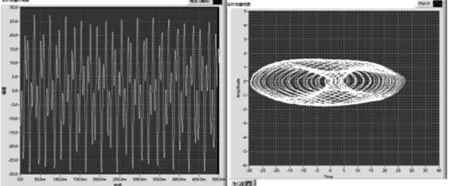
(c) f=128 Hz,T=1.40 N,β=0.18,時域圖及相圖

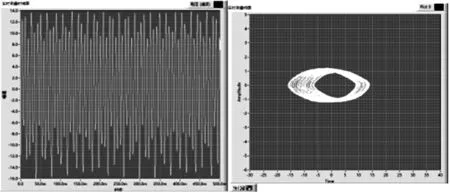
(d) f=128 Hz,T=1.40 N,β=0.48,時域圖及相圖

4 結論

本實驗根據弦線非線性振動理論，結合硬件及軟件設計兩方面，構建了一套學習和分析該系統中混沌現象的方案，能直觀地觀察和定量研究該系統由混沌運動向周期有序運動相互轉換的過程.當弦線和連接點調整到接近駐波波腹處，弦線處于穩定的振動狀態，而調節到接近駐波波節處時，振動系統處于不穩定運動狀態.實驗中β值在(0.18，0.21)或(0.78，0.81)范圍時形成了混沌現象，此時系統的運動過程對初值的依賴性十分敏感.實驗裝置混沌現象的理論模型和實測數據及實時觀察的混沌現象比較吻合.