關(guān)于輕桿上的力方向的思考

余 輝

(烏魯木齊八一中學(xué) 新疆 烏魯木齊 830002)

1 輕桿上力的認(rèn)識(shí)

高中物理中，在彈力這一節(jié)第一次認(rèn)識(shí)輕桿模型，我們知道它不同于輕繩模型，它的力可以沿著桿向里，也可以沿著桿向外，也可以不沿桿. 所以一開(kāi)始它就和輕繩同時(shí)出現(xiàn)，對(duì)比著學(xué)習(xí)來(lái)記憶.學(xué)生一開(kāi)始學(xué)到這里會(huì)覺(jué)得桿模型難以理解，做題時(shí)不容易判斷桿上力的方向.常見(jiàn)出題模型如下.

(1)圖1中左側(cè)為墻壁，輕繩一端固定在墻上，通過(guò)光滑定滑輪吊一個(gè)重物，輕桿左端固定在墻上，右端固定輕質(zhì)定滑輪.

圖1 常見(jiàn)出題模型一

(2)圖2中左側(cè)為墻壁，輕桿左端通過(guò)鉸鏈拴接在墻上，右端分別與兩根輕繩相連.

圖2 常見(jiàn)出題模型二

兩個(gè)圖中物體質(zhì)量均為m，輕繩與墻壁夾角均為θ=60°，重力加速度為g，求解輕桿對(duì)輕繩的彈力.

分析：圖1中輕桿無(wú)法轉(zhuǎn)動(dòng)，所以輕桿右端受到的力可以沿著桿也可以不沿桿，又因?yàn)橛叶耸枪饣幕啠岳K子拉力大小處處相等，對(duì)繩子上與滑輪接觸點(diǎn)受力分析如圖3所示，從而求得繩子拉力T大小為mg，方向向左上方與水平方向夾角為30°，由平衡條件，輕桿上的滑輪對(duì)輕繩的彈力F大小為mg，向右上方，與水平方向夾角為30°.

圖3 圖1中繩子上與滑輪接觸點(diǎn)受力分析

圖4 圖2中輕繩上與輕桿右端接觸點(diǎn)受力分析

這是關(guān)于輕桿的非常經(jīng)典的習(xí)題，輕桿上的力是否沿桿是一個(gè)難點(diǎn).正因?yàn)檫@個(gè)難點(diǎn)，在后面的圓周運(yùn)動(dòng)的學(xué)習(xí)中會(huì)碰到類似的難點(diǎn)問(wèn)題.

2 圓周運(yùn)動(dòng)中輕桿模型的疑惑

圖5 豎直平面內(nèi)圓周運(yùn)動(dòng)模型

圖5中，以圓心為轉(zhuǎn)軸，在最高點(diǎn)時(shí)輕桿與小球系統(tǒng)受到重力過(guò)圓心，所以力矩M為零，系統(tǒng)轉(zhuǎn)動(dòng)慣量I=mR2(忽略輕桿質(zhì)量)不為零，則根據(jù)公式M=Iβ知β=0，再根據(jù)公式at=Rβ可知切向加速度為零，則最高點(diǎn)時(shí)切向沒(méi)有加速度，也就沒(méi)有力的作用，輕桿給小球的力一定沿著桿.這樣就解決了我們之前的疑惑.

3 拓展

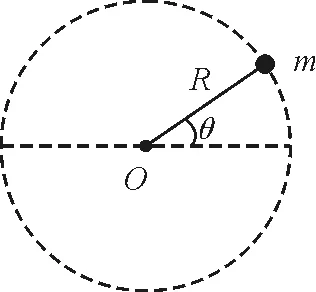
圖6 問(wèn)題拓展示意圖一

進(jìn)一步拓展，在機(jī)械能守恒中我們常常會(huì)碰到如圖7所示模型，輕桿兩邊分別連接質(zhì)量為m和2m的小球，輕桿可以繞位于圓心的軸無(wú)摩擦的轉(zhuǎn)動(dòng)，圓半徑為R，初速度為零釋放，在最低點(diǎn)時(shí)輕桿對(duì)質(zhì)量為m的小球彈力為多大？這個(gè)問(wèn)題求解并不難，我們只需要利用機(jī)械能守恒解出m運(yùn)動(dòng)到最高點(diǎn)時(shí)的速度，再利用向心力公式就可以求出彈力，這里我們也是默認(rèn)最高點(diǎn)時(shí)輕桿給小球m的彈力是沿著桿的.但是在m向上運(yùn)動(dòng)過(guò)程中，輕桿給小球的力并不沿著桿，因?yàn)樾∏騧動(dòng)能增加，重力又對(duì)它做負(fù)功，則輕桿對(duì)小球m必然做正功，輕桿給的力不可能始終垂直于速度，也就是不能始終沿著桿.

圖7 問(wèn)題拓展示意圖二

既然之前輕桿對(duì)小球做正功了，為什么在最高點(diǎn)時(shí)就默認(rèn)輕桿對(duì)小球的力就沿著桿了呢？這里我們也需要利用角動(dòng)量定理來(lái)解釋，當(dāng)m球轉(zhuǎn)到最高點(diǎn)時(shí)2m球在最低點(diǎn)，以圓心為軸這個(gè)整體受到外力都經(jīng)過(guò)圓心，所以力矩M為零，則角加速度β=0，切向加速度at=0，則輕桿給小球的力一定沿著桿方向.

由此，我們通過(guò)競(jìng)賽中常用的角動(dòng)量定理解釋了我們?cè)谳p桿模型中這幾點(diǎn)疑惑.在教學(xué)中我們經(jīng)常會(huì)碰到一些考試中不太會(huì)考到的問(wèn)題，考試中幾乎不出現(xiàn)導(dǎo)致我們也并不重視，但是這些問(wèn)題的確是存在的，學(xué)生會(huì)問(wèn)，我們自己也會(huì)很疑惑.這時(shí)候就需要學(xué)習(xí)一些新的知識(shí)來(lái)幫我們徹底解決.這樣我們腦海中的知識(shí)體系才能完整.