從問題開始，讓學習走向深入

施婭林

英國科學家培根曾說過：“如果你從肯定開始，必將以問題告終;如果從問題開始，則將以肯定結(jié)束。”對學生而言，單單獲得一個結(jié)論，并不意味著他們掌握了知識。真正有效的學習過程，是培養(yǎng)發(fā)現(xiàn)并解決問題的能力。于是，筆者對“3的倍數(shù)特征”再思考，試著從關(guān)注兒童問題的角度思考這節(jié)課。

一、初教學：觸于“表”難及“里”引發(fā)的問題

在蘇教版五年級下冊“3的倍數(shù)特征”這一課中，教材給學生提供了多種探究素材，如百數(shù)表（圖略），先找到相應(yīng)的3的倍數(shù)，再通過觀察從個位上看不出3的倍數(shù)特征，引導學生猜測并驗證自己的猜想，從而總結(jié)出3的倍數(shù)特征。

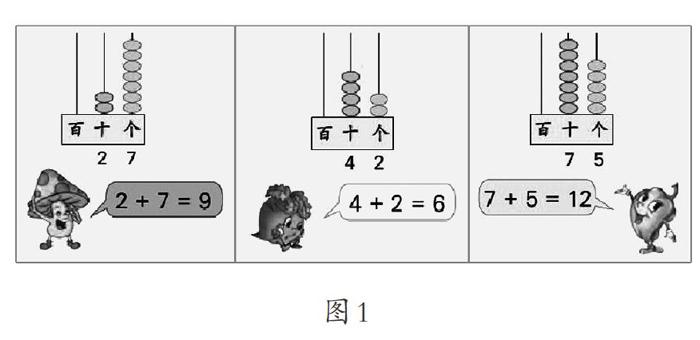
再如計數(shù)器（圖1）：先撥出3的倍數(shù)，再數(shù)出所用算珠總數(shù)，以此抽象出各個數(shù)位上數(shù)字和的特點。

由于部分學生課前已有知識基礎(chǔ)，很快就記住了3的倍數(shù)特征。這時候，有個學生突然問道：“為什么一個數(shù)各位上數(shù)的和是3的倍數(shù)，這個數(shù)就是3的倍數(shù)啊？”

課后，筆者思考：當新知與之前學習2和5的倍數(shù)特征不一致的情況下，學生會出現(xiàn)思維的“盲點”，他們很難通過“根據(jù)一個數(shù)的各位上數(shù)的和是否是3的倍數(shù)”來進行判斷，而且并不理解3的倍數(shù)特征為什么是各位上數(shù)的和是3的倍數(shù)。那么，有沒有必要回到思維的原點，從數(shù)學本質(zhì)的角度來回答那個學生的問題呢？特級教師賁友林在《賁友林與學為中心數(shù)學課堂》這本書中提出：對數(shù)學內(nèi)容的理解，有“工具性理解”與“關(guān)系性理解”兩種模式。“工具性理解”是對數(shù)學對象的表層理解，只知道做什么，不知道為什么這樣做;而“關(guān)系性理解”是對數(shù)學本質(zhì)的把握，“不僅知道要做什么，而且知道理由”。因此，數(shù)學研究只知道“是什么”是不夠的，我們要沿著教材脈絡(luò)大膽地進行再探究。

二、再出發(fā)：研究問題，由淺入深，觸及本質(zhì)

師：我們今天就來探究“為什么一個數(shù)各位上數(shù)的和是3的倍數(shù)，這個數(shù)就是3的倍數(shù)”這個問題，選擇你喜歡的方式來進行研究。

（學生自主探究后匯報）

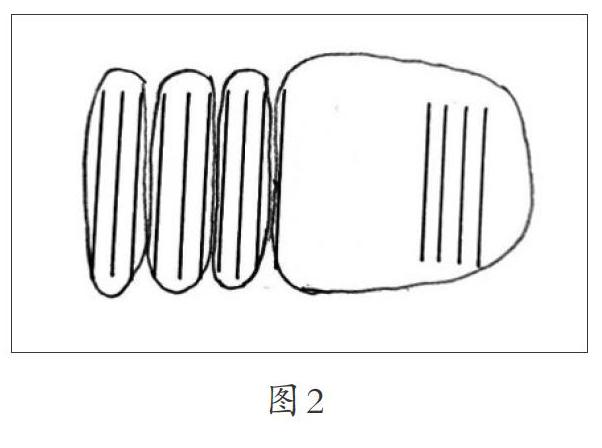
生：我是通過畫小棒圖來研究的，如圖2，畫了14根小棒，一捆是10根，拆開3根3根地分，還會剩下1根，這剩下的1根和其余的4根合在一起，可以看成1加4等于5，5不是3的倍數(shù)，所以14不是3的倍數(shù)。

生：如果是24根小棒，也是同樣的道理（如圖3），可知24是3的倍數(shù)。

生：用字母a，b，c表示出了一個三位數(shù)（如圖4），百位上的a表示a個百，十位上的b表示b個十，個位上的c表示c個一，把這個三位數(shù)拆分就可以寫成100a+10b+c。99和9是3的倍數(shù)，100a分成99a+a，10b分成9b+b， 99a和9b肯定是3的倍數(shù)，只要看a+b+c是不是3的倍數(shù)就行了。

師：今天研究的是3的倍數(shù)特征，用這樣的方法還能找到其他數(shù)的倍數(shù)特征嗎？比如說4的倍數(shù)特征。

……

原本只是解決那個學生提出的問題，結(jié)果衍生出了后續(xù)這么多的精彩問題。所以，問題不是壁壘，更不是終點。相反，問題是內(nèi)驅(qū)，是動力，也是研究的方向，問題終將引領(lǐng)我們走進更美好的數(shù)學課堂。

三、再思考：從學生的問題開始，讓學習走向深入

關(guān)注學生的問題，其實就是為學生深入學習知識本質(zhì)提供了契機。那么，在教學時如何應(yīng)對學生的問題？

1.重視學生的問題，順問引導。筆者在初次教學時忽視了學生的問題，以淺顯的發(fā)現(xiàn)和個別學生的答案代替了學生對知識的理解。其實大部分學生對“3的倍數(shù)特征”這一知識并不理解，只是簡單套用公式，這不利于學生的思維發(fā)展。于是，在經(jīng)過思考后，筆者重新出發(fā)，重視學生的問題，對學生進行引導，由淺入深，觸及本質(zhì)。理解并掌握了“3的倍數(shù)特征”后，引發(fā)學生思考“4的倍數(shù)特征”“6的倍數(shù)特征”等問題。這樣教師的引導會讓問題更豐富，讓數(shù)學課堂更豐實。

2.深入研究學生的問題， 順問學習。在上述再出發(fā)的教學過程中，圍繞著學生的問題“為什么一個數(shù)是否是3的倍數(shù)要看這個數(shù)各位上數(shù)的和”展開深入研究，充分讓學生在做中學，在學中思，在思中辨。我們也看到學生由直觀的舉例，自然地過渡到抽象的字母表達式，體現(xiàn)了從特殊到一般的數(shù)學思想。“3的倍數(shù)特征”這個概念確實比較抽象，學生難以理解，如果借助直觀的畫圖、舉例、對數(shù)的拆分，觸及知識背后的本質(zhì)，學生就能真正理解與掌握知識。

（作者單位：南京外國語學校河西初級中學第一附屬小學）

投稿郵箱：405956706@qq.com