無(wú)人傾轉(zhuǎn)旋翼機(jī)直升機(jī)模式縱向位置控制律設(shè)計(jì)

梁天，肖斯奇，施嘯宇

( 南京航空航天大學(xué) 自動(dòng)化學(xué)院，江蘇 南京 210016)

0 引言

傾轉(zhuǎn)旋翼機(jī)能夠像直升機(jī)一樣垂直起降與懸停，也能像固定翼飛機(jī)一樣高速巡航，兼具直升機(jī)和固定翼的優(yōu)點(diǎn)，與常規(guī)直升機(jī)相比，其飛行速度、航程都大幅增加；與固定翼飛機(jī)相比，無(wú)需長(zhǎng)跑道，起降適應(yīng)性強(qiáng)，其飛行包線涵蓋了直升機(jī)和固定翼的范圍。因?yàn)槠鋬?yōu)異的性能和良好的經(jīng)濟(jì)性，無(wú)論是在軍用還是民用領(lǐng)域都具有廣闊的發(fā)展空間。隨著飛行控制技術(shù)的研究發(fā)展，無(wú)人傾轉(zhuǎn)旋翼機(jī)也開(kāi)始進(jìn)入快速發(fā)展階段[1]。

傾轉(zhuǎn)旋翼機(jī)旋翼短艙與機(jī)體垂直時(shí)定義為直升機(jī)模式，直升機(jī)模式是無(wú)人傾轉(zhuǎn)旋翼機(jī)飛行階段不可或缺的一環(huán),也是顯著區(qū)別于固定翼飛機(jī)的特點(diǎn)。在起降、懸停或低速飛行時(shí)，其整機(jī)的升力、操縱力/力矩均來(lái)自位于左右機(jī)翼末端的兩副旋翼，針對(duì)此模式的控制律設(shè)計(jì)具有工程上的實(shí)用價(jià)值。

目前，對(duì)于無(wú)人傾轉(zhuǎn)旋翼機(jī)控制方案的研究關(guān)注度均集中在傾轉(zhuǎn)過(guò)渡段，對(duì)于直升機(jī)模式的控制問(wèn)題鮮有深入研究，而直升機(jī)模式的控制決定其起降性能。因此本文將通過(guò)分析直升機(jī)模式縱向特性，研究縱向位置控制律的控制策略，優(yōu)化縱向位置控制律，并結(jié)合實(shí)時(shí)仿真驗(yàn)證控制律設(shè)計(jì)的魯棒性。

1 建模與對(duì)象特性分析

1.1 建模

本文沿用實(shí)驗(yàn)室目前在旋翼類(lèi)飛行器中所獲得的技術(shù)積累，使用專(zhuān)業(yè)旋翼類(lèi)飛機(jī)建模軟件RotorLib，采用機(jī)理法進(jìn)行建模。根據(jù)直升機(jī)空氣動(dòng)力學(xué)原理和機(jī)械運(yùn)動(dòng)原理，構(gòu)建直升機(jī)模式的運(yùn)動(dòng)方程，描述其運(yùn)動(dòng)機(jī)理。利用動(dòng)量理論和葉素理論計(jì)算旋翼氣動(dòng)力，并綜合考慮了旋翼高階運(yùn)動(dòng)特性和氣動(dòng)部件之間的干擾，對(duì)影響旋翼建模動(dòng)力學(xué)特性的因素進(jìn)行相對(duì)全面的處理。其建模結(jié)果目前已經(jīng)歷數(shù)個(gè)型號(hào)機(jī)型的試飛，具有較高的置信度[2-3]。

本文所采用的對(duì)象無(wú)人傾轉(zhuǎn)旋翼機(jī)模型用歐美坐標(biāo)系下的懸停狀態(tài)數(shù)學(xué)模型形式為：

(1)

1.2 縱向模態(tài)分析

表1為直升機(jī)模式縱向特征根。

表1 直升機(jī)模式縱向特征根

俯仰阻尼模態(tài)物理解釋為，若受擾動(dòng)后做俯仰運(yùn)動(dòng)，俯仰角和旋翼迎角發(fā)生變化，然而旋翼具有較大的氣動(dòng)阻尼以及氣動(dòng)上機(jī)翼和平尾提供額外的俯仰阻尼使得俯仰角的變化快速衰減。

前向速度振蕩模態(tài)主要描述了縱向速度和旋翼迎角的變化關(guān)系。比如當(dāng)傾轉(zhuǎn)旋翼機(jī)懸停時(shí)受到擾動(dòng)產(chǎn)生前向速度，旋翼會(huì)由于相對(duì)氣流發(fā)生后倒，整個(gè)旋翼產(chǎn)生向后上方的力。該力的水平分量使直升機(jī)前向加速度減小直至為0，而此時(shí)直升機(jī)前向速度達(dá)到最大值，旋翼相對(duì)氣流速度也達(dá)到最大。因此旋翼繼續(xù)后倒，此時(shí)旋翼產(chǎn)生升力的水平分量使直升機(jī)產(chǎn)生向后的加速度直至前向速度過(guò)零點(diǎn)之后反向，由于對(duì)象傾轉(zhuǎn)旋翼機(jī)不穩(wěn)定，因此反向最大速度會(huì)大于前向速度。以上的過(guò)程周而復(fù)始，最終發(fā)散，并且此模態(tài)耦合俯仰角和高度通道。可得出結(jié)論，對(duì)象無(wú)人傾轉(zhuǎn)旋翼機(jī)縱向穩(wěn)定性差，所以需引入俯仰角反饋與前向速度反饋，提高縱向的穩(wěn)定性[4-5]。

觀察縱向周期變距到角速率的開(kāi)環(huán)頻域響應(yīng)(圖1)，低頻段較小幅值增益反映出姿態(tài)跟蹤能力弱，穩(wěn)態(tài)控制精度低等，難以實(shí)現(xiàn)精確跟蹤控制。因此可以預(yù)測(cè)在低頻輸入下響應(yīng)特性差，抗干擾能力弱。頻率響應(yīng)特性的分析為控制律設(shè)計(jì)提供了理論依據(jù)。

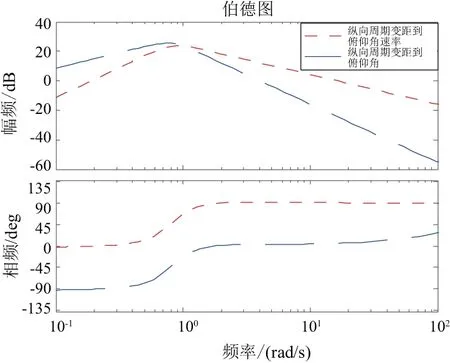
圖1 開(kāi)環(huán)頻域特性曲線

1.3 控制需求分析

縱向位置控制的主要任務(wù)是控制無(wú)人傾轉(zhuǎn)旋翼機(jī)的縱向空間位置，是直升機(jī)模式所特有的控制要求，ADS-33直升機(jī)飛行品質(zhì)規(guī)范中對(duì)位置控制精度也有明確的規(guī)定[6]。在縱向通道上要保持縱向位置不變或者小速度前飛/后飛。按照兩種要求將縱向分為保持狀態(tài)和跟蹤狀態(tài)。保持狀態(tài)的控制任務(wù)是保持縱向位置不變，跟蹤狀態(tài)的控制任務(wù)是實(shí)現(xiàn)無(wú)人直升機(jī)空間位置的小速度移動(dòng)。

從縱向通道本身特性來(lái)看，存在俯仰阻尼模態(tài)和速度震蕩模態(tài)，但是為確保位置響應(yīng)的平穩(wěn)性，位置回路阻尼比需要≥1.0。其次，需要具有較強(qiáng)的適應(yīng)能力，才能夠滿足在不同環(huán)境下例如風(fēng)擾動(dòng)和信號(hào)干擾等情況下的控制性能要求。

2 縱向位置控制策略研究

2.1 基于姿態(tài)角阻尼內(nèi)回路的位置控制

姿態(tài)阻尼內(nèi)回路位置控制是使用增穩(wěn)回路來(lái)提高系統(tǒng)穩(wěn)定性，不進(jìn)行姿態(tài)角跟蹤控制。外回路采用位置保持與跟蹤控制回路，為PID控制器，并且外回路被控量不產(chǎn)生姿態(tài)指令，直接輸出到舵面進(jìn)行控制[7]。控制律為

δe=δetrim+Kθ·(θ-θtrim)+Kq·q-

(2)

基于姿態(tài)角阻尼內(nèi)回路位置控制對(duì)應(yīng)的控制結(jié)構(gòu)如圖2所示。

圖2 基于姿態(tài)角阻尼內(nèi)回路位置控制結(jié)構(gòu)圖

2.2 基于姿態(tài)角指令內(nèi)回路的位置控制

姿態(tài)角指令內(nèi)回路將位置回路產(chǎn)生的控制量轉(zhuǎn)換為姿態(tài)角指令，通過(guò)內(nèi)回路的姿態(tài)精確控制間接實(shí)現(xiàn)位置控制。此控制結(jié)構(gòu)對(duì)姿態(tài)角內(nèi)回路的控制精度的要求較高，因此需要引入姿態(tài)角積分量來(lái)保證控制精度。控制律為：

(3)

基于姿態(tài)角指令內(nèi)回路的位置控制對(duì)應(yīng)的控制結(jié)構(gòu)如圖3所示。

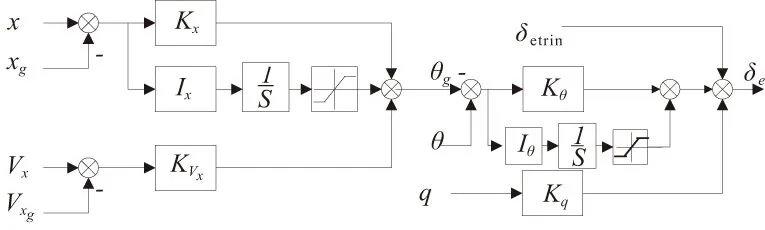
圖3 基于姿態(tài)角指令內(nèi)回路位置控制結(jié)構(gòu)圖

2.3 基于地速的高精度位置控制律

相比于姿態(tài)角指令，內(nèi)回路的位置控制是通過(guò)內(nèi)回路的姿態(tài)精確控制間接實(shí)現(xiàn)位置控制。基于地速的高精度位置控制律是通過(guò)地速的精確控制間接實(shí)現(xiàn)位置控制。內(nèi)回路采用姿態(tài)增穩(wěn)回路，提高姿態(tài)回路穩(wěn)定性；外回路為地速控制回路，采用PI控制器實(shí)現(xiàn)地速保持與跟蹤控制。

(4)

基于地速的高精度位置控制對(duì)應(yīng)的控制結(jié)構(gòu)如圖4所示。

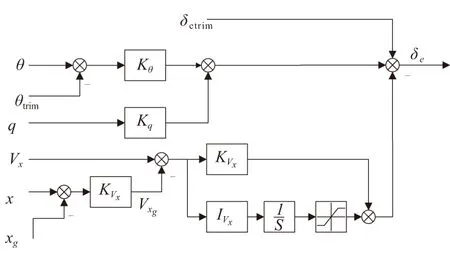
圖4 基于地速高精度位置控制結(jié)構(gòu)圖

2.4 控制策略對(duì)比

首先基于姿態(tài)角阻尼內(nèi)回路的位置控制避開(kāi)無(wú)人傾轉(zhuǎn)旋翼機(jī)姿態(tài)難準(zhǔn)確跟蹤的問(wèn)題，工程實(shí)現(xiàn)較為簡(jiǎn)單，且姿態(tài)響應(yīng)比較平緩，在此方面有利于降低機(jī)身震動(dòng)。但是需要通過(guò)位置偏差建立新的配平舵面，其抗擾動(dòng)能力較差。

基于姿態(tài)角指令內(nèi)回路的位置控制因?yàn)橥ㄟ^(guò)姿態(tài)環(huán)建立配平狀態(tài)，所以抗擾動(dòng)能力較強(qiáng)，但是姿態(tài)控制難度大，工程實(shí)現(xiàn)較困難，且和姿態(tài)角阻尼內(nèi)回路相反，姿態(tài)波動(dòng)較大，容易加劇機(jī)體震動(dòng)。

基于地速控制的位置控制姿態(tài)響應(yīng)平緩，因?yàn)槭峭ㄟ^(guò)地速控制來(lái)間接控制位置，精度更高，且抗風(fēng)性更強(qiáng)。除此之外，在不接入位置環(huán)的情況下，地速控制還可以實(shí)現(xiàn)相對(duì)位置的懸停功能。

根據(jù)以上分析最終選擇基于地速控制的位置控制律并進(jìn)行參數(shù)設(shè)計(jì)和工程實(shí)現(xiàn)。

3 基于地速的高精度位置控制律設(shè)計(jì)

基于地速的高精度位置控制律內(nèi)回路采用姿態(tài)增穩(wěn)回路，外回路由兩部分組成：地速控制回路和位置控制回路。可從內(nèi)由外進(jìn)行設(shè)計(jì)。

3.1 姿態(tài)增穩(wěn)內(nèi)回路

采用角速率和姿態(tài)角的姿態(tài)增穩(wěn)內(nèi)回路，回避了傾轉(zhuǎn)旋翼機(jī)直升機(jī)模式懸停時(shí)姿態(tài)控制的難點(diǎn)。由于不需要進(jìn)行精確控制，姿態(tài)內(nèi)回路不需要加入積分項(xiàng)，僅采用比例和微分兩項(xiàng)進(jìn)行增穩(wěn)，即可滿足姿態(tài)增穩(wěn)的要求。俯仰角速率的反饋能夠快速抑制縱向短周期的俯仰角速率振蕩，提高縱向短周期角運(yùn)動(dòng)阻尼；俯仰角信號(hào)也以并聯(lián)形式接入增穩(wěn)回路，用于彌補(bǔ)對(duì)象傾轉(zhuǎn)旋翼機(jī)俯仰運(yùn)動(dòng)靜穩(wěn)定性的不足，改善縱向長(zhǎng)周期響應(yīng)的阻尼比。

傾轉(zhuǎn)旋翼機(jī)縱向的動(dòng)力學(xué)方程為

m(ax-Vyq+Vzr)+mgsinθ=Tsinθ

(5)

觀察方程，俯仰角θ與縱向加速度ax存在比例關(guān)系，從而可以認(rèn)為俯仰角是速度的加速度項(xiàng)。阻尼內(nèi)回路選擇的俯仰角系數(shù)越大，對(duì)地速控制來(lái)講，阻尼越強(qiáng)，即抗干擾能力越強(qiáng)。但是過(guò)大的系數(shù)會(huì)導(dǎo)致出舵量較大，所以需綜合考慮后選取參數(shù)。

從力方面考慮，如圖5所示，除縱向周期變距改變引起的前向力，Δθ會(huì)讓拉力在水平面產(chǎn)生前向分力TsinΔθ，此分力會(huì)產(chǎn)生前向加速度ax，俯仰角引起的前向加速度會(huì)引起前向速度的增加，從而使地速的響應(yīng)加快。

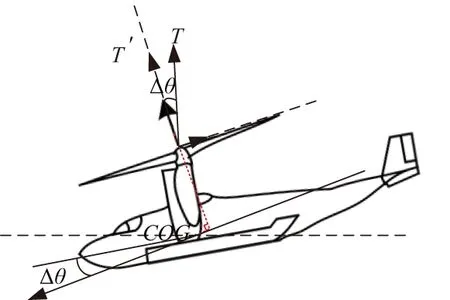
圖5 改變俯仰角引起的力變化示意圖

從圖6可以看出，當(dāng)內(nèi)環(huán)接入俯仰角阻尼內(nèi)回路后，比較原始縱向周期變距到縱向速度的開(kāi)環(huán)頻域響應(yīng)，相位出現(xiàn)明顯的超前調(diào)整，證明接入俯仰角阻尼內(nèi)回路后，前向速度的響應(yīng)變快，改善了地速回路的頻域特性[8]。

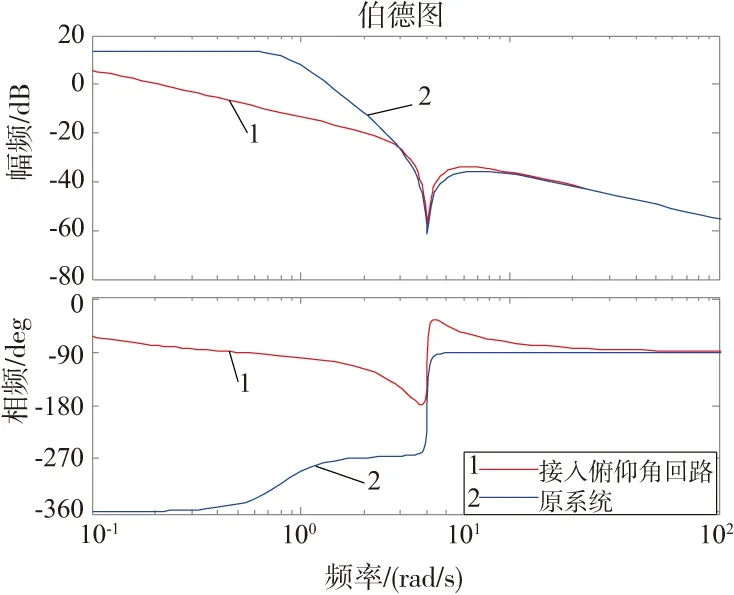
圖6 接入俯仰角前后的速度頻域響應(yīng)對(duì)比

如圖7所示，接入俯仰角后的根軌跡曲線，最終設(shè)計(jì)阻尼內(nèi)回路參數(shù)Kq的值為0.2，Kθ的值為0.35。

圖7 接入俯仰角后的根軌跡圖

3.2 地速控制回路

地速控制回路為地速偏差的PI控制，并且外回路對(duì)位置的控制實(shí)際上也是間接通過(guò)地速的指令值來(lái)進(jìn)行準(zhǔn)確控制的。所以在整個(gè)位置控制中，地速回路為絕對(duì)的核心。

地速回路的積分項(xiàng)設(shè)計(jì)，需要著重從整個(gè)地速回路的抗干擾能力來(lái)進(jìn)行設(shè)計(jì)，在此基礎(chǔ)上考慮整個(gè)地速通道的快速性和穩(wěn)定性。

從圖8的地速回路根軌跡來(lái)看，包含姿態(tài)增穩(wěn)后的系統(tǒng)長(zhǎng)周期穩(wěn)定，在調(diào)參過(guò)程中可以發(fā)現(xiàn)，縱向速度積分增益越大，階躍響應(yīng)上升時(shí)間越短，系統(tǒng)響應(yīng)越快。但過(guò)大的積分增益同時(shí)導(dǎo)致系統(tǒng)的動(dòng)態(tài)響應(yīng)性能變差，速度振蕩變大，需要加大比例增益抑制振蕩，整個(gè)響應(yīng)的調(diào)節(jié)時(shí)間變長(zhǎng)。減小積分增益可以改善縱向速度響應(yīng)的振蕩，但同時(shí)其響應(yīng)速度也變慢，上升時(shí)間變長(zhǎng)，系統(tǒng)跟蹤能力弱，綜合考慮系統(tǒng)調(diào)節(jié)時(shí)間和超調(diào)振蕩等因素，將速度控制回路的系數(shù)定為KVX=0.9，IVX=0.12，此時(shí)縱向速度的階躍曲線如圖9所示。從階躍響應(yīng)圖中可以看出，縱向速度階躍響應(yīng)超調(diào)很小，調(diào)節(jié)時(shí)間為7s左右，系統(tǒng)響應(yīng)性能比較理想。

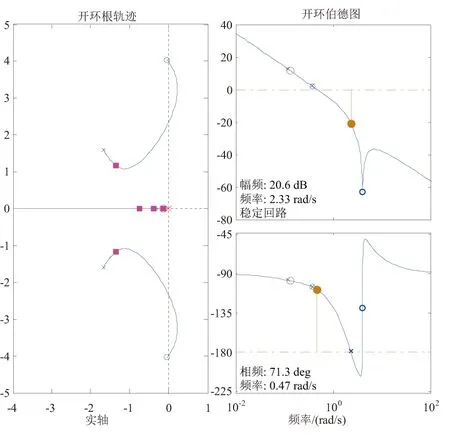
圖8 地速回路根軌跡曲線

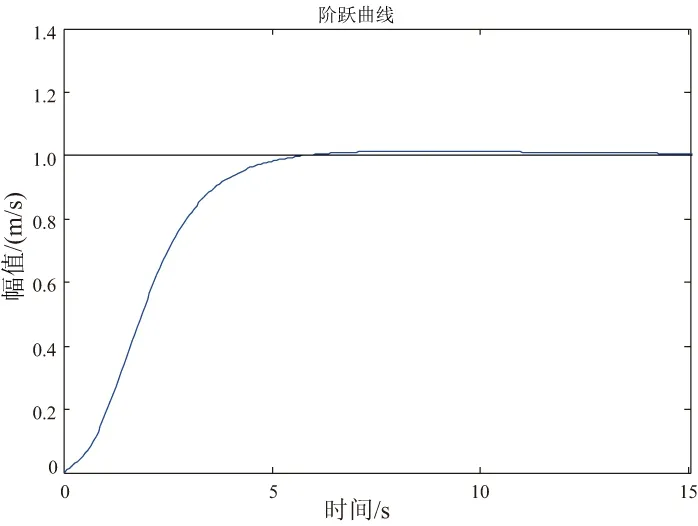
圖9 地速回路階躍響應(yīng)曲線

3.3 位置控制回路

地速控制回路僅解決地速跟蹤的問(wèn)題，對(duì)絕對(duì)位置的跟蹤需要位置回路的加入。位置控制結(jié)構(gòu)較為簡(jiǎn)單，將位置偏差信號(hào)給到速度指令值進(jìn)行控制即可。

位置控制最終達(dá)到的目標(biāo)是滿足位置響應(yīng)的準(zhǔn)確性和平穩(wěn)性[9]。結(jié)合圖10最終的時(shí)域階躍響應(yīng)進(jìn)行參數(shù)選擇Kx=0.18。

圖10 位置回路階躍響應(yīng)曲線

4 仿真性能驗(yàn)證

無(wú)人傾轉(zhuǎn)旋翼機(jī)直升機(jī)模式位置控制的主要問(wèn)題之一是其在懸停飛行模態(tài)時(shí)，對(duì)大氣擾動(dòng)的抵抗能力不足，容易出現(xiàn)較大的控制誤差。因此，本文著重針對(duì)這一問(wèn)題，設(shè)計(jì)仿真案例進(jìn)行驗(yàn)證控制律設(shè)計(jì)的正確性[10-11]。

魯棒性測(cè)試采用3種手段，分別是5m/s的常值風(fēng)，幅值為8m/s的正弦風(fēng)，最后模擬地速死區(qū)為0.03m/s。仿真結(jié)果位置偏差曲線和縱向速度曲線如圖11-圖13所示。

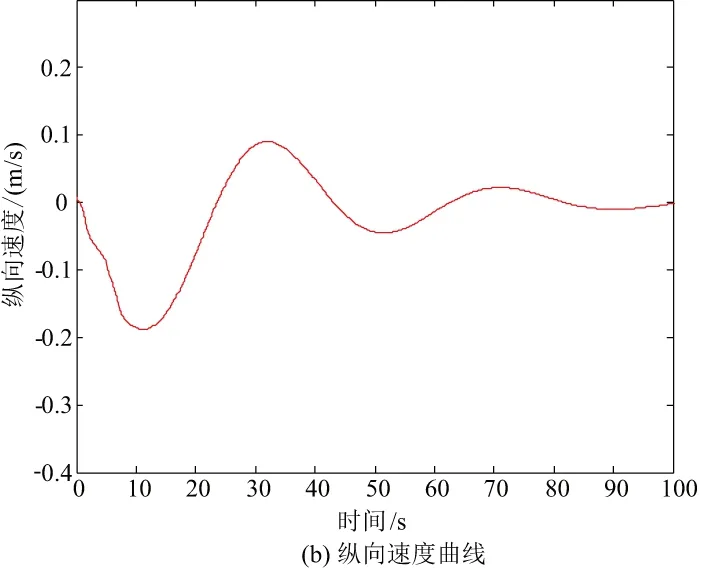
圖11 常值風(fēng)5m/s位置和速度曲線

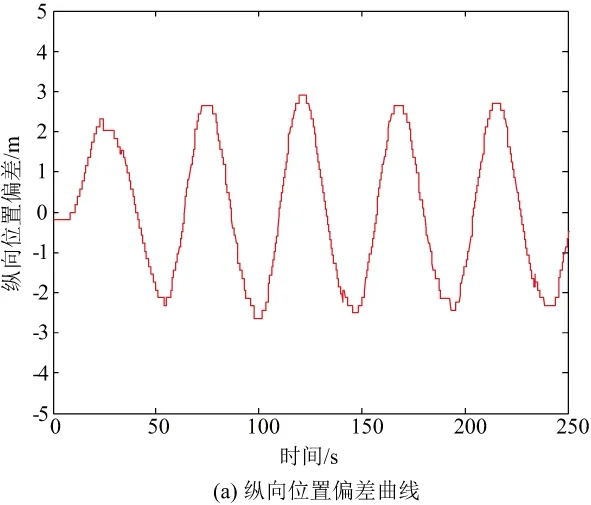
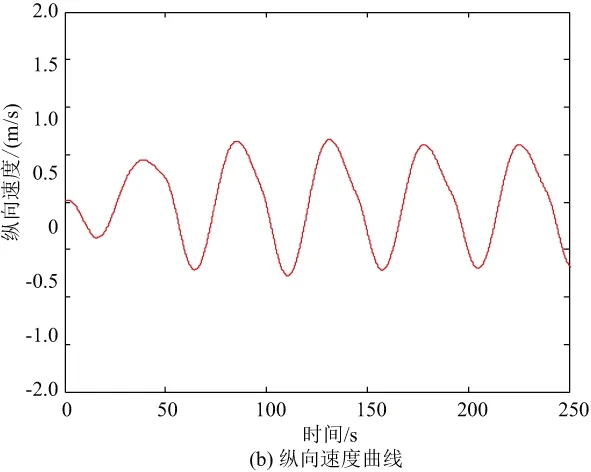
圖12 正弦風(fēng)8m/s位置和速度曲線

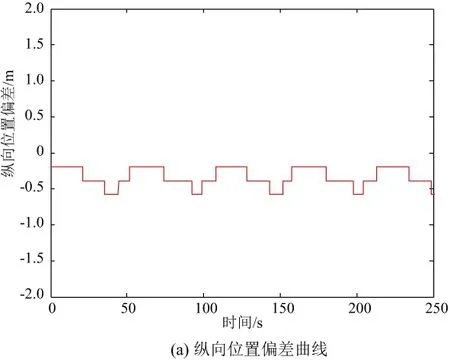
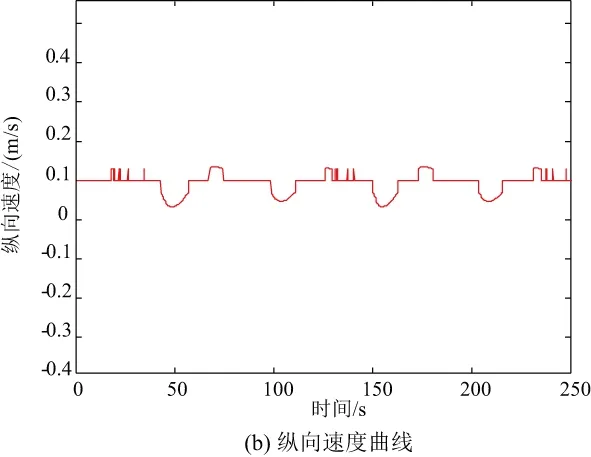
圖13 地速死區(qū)0.03m/s位置和速度曲線

觀察仿真結(jié)果曲線，基于地速的高精度位置控制律能夠很好地完成縱向位置控制，且具有優(yōu)秀的抗干擾能力。

5 結(jié)語(yǔ)

本文針對(duì)無(wú)人傾轉(zhuǎn)旋翼機(jī)直升機(jī)模式的縱向位置控制，選取基于地速的高精度位置控制律為控制策略，從根軌跡和物理概念角度設(shè)計(jì)控制內(nèi)外環(huán)參數(shù)，最終通過(guò)非線性仿真驗(yàn)證控制律的魯棒性，完成了縱向位置的控制律設(shè)計(jì)。