基于內聚力模型的輪盤破裂轉速預測方法研究

黃紅梅，趙凱，賈文斌，潘磊，方磊，周柏卓

(1. 南京航空航天大學 江蘇省航空動力系統重點實驗室，江蘇 南京 210016；2. 中國航空發動機集團 沈陽發動機設計研究所，遼寧 沈陽 110015)

0 引言

航空發動機的核心部件，如壓氣機盤和渦輪盤的可靠性直接影響飛行器的安全。由于壓氣機盤和渦輪盤承受復雜的載荷，即使在滿足靜強度要求的條件下，也會發生疲勞失效以至破裂。因此，研究輪盤的破裂轉速對預測壓氣機盤和渦輪盤的破裂轉速具有重要意義。

斷裂力學是研究結構和材料失效的一門學科，但傳統斷裂力學不適用于大范圍屈服構件或整體屈服構件。近年來，基于彈塑性斷裂力學的內聚力模型(cohesive zone model，CZM)因其模擬裂紋擴展簡單且有效而廣泛應用。內聚力模型的概念由BARENBLATT G I[1-2]提出，并考慮了脆性材料的有限強度。DUGDALE D S[3]將內聚力模型用于研究裂紋尖端的屈服及塑性區的尺寸。HILLERBORG A等[4]率先將內聚力模型用于研究混凝土材料的斷裂過程。內聚力模型常常用于模擬事先已知裂紋路徑的裂紋擴展過程[2-3]。廣泛使用的內聚力模型有雙線性內聚力模型(bilinear cohesive zone model)[5]、梯形內聚力模型(trapezoidal cohesive zone model)[6]、光滑梯形內聚力模型(softening trapezoidal cohesive zone model)[7]、指數內聚力模型(exponential cohesive zone model)[8]、多項式內聚力模型(polynomial cohesive zone model)[9]等。內聚力模型已成功用于研究各種材料的裂紋擴展，如復合材料[10]、非均質材料[11]、瀝青混凝土[12]及粘接界面[13]等。

BERT C W和PAUL T K[14]基于平面彈性理論研究輪盤破裂轉速時，未考慮裂紋擴展的影響。本文以含徑向初始裂紋的輪盤為研究對象，引入內聚力模型模擬輪盤的裂紋擴展過程并預測破裂轉速，驗證內聚力模型的有效性。

1 旋轉輪盤破裂轉速理論解

BERT C W和PAUL T K將旋轉輪盤問題簡化為二維平面彈性問題，推導了含初始徑向裂紋旋轉輪盤上的應力分布如下：

式中：σr、σθ、τrθ、σeff分別為徑向應力、周向應力、切向應力和Mises應力；ρ為密度；ω為轉速；r、θ分別為極坐標下的極徑與極角；A、B、D為常數項，由下列邊界條件求得：

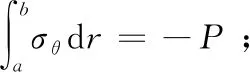
3) 當r=r2時，τrθ=0。

由公式(1)、邊界條件2)可求出等效載荷P。應力強度因子的表達式如下：

(2)

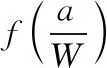
(3)

KQ可由材料的斷裂韌度KIC代替，其余參數如圖1所示。根據等效載荷P估算力矩M：

M=P(r1+r2)/2

(4)

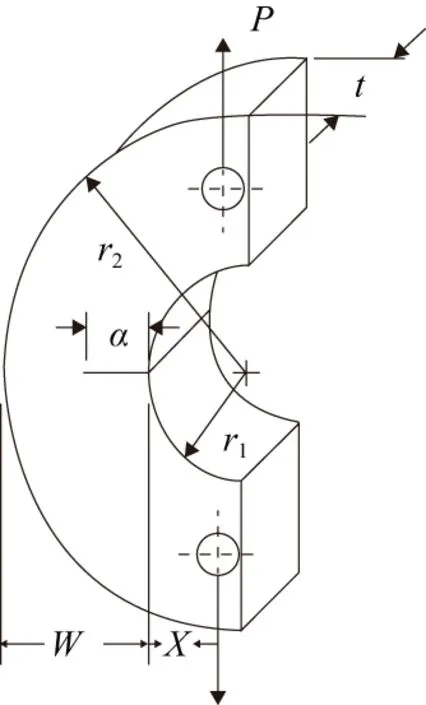
圖1 計算模型

隨著輪盤轉速增加，輪盤上的Mises應力增加，當Mises應力最大值達到屈服極限σut時，對應轉速即為破裂轉速。圖2所示為輪盤內徑處的應力分布曲線。隨著θ值的增加，Mises應力先增加后減小，當θ=90°時，Mises應力達到最大值。

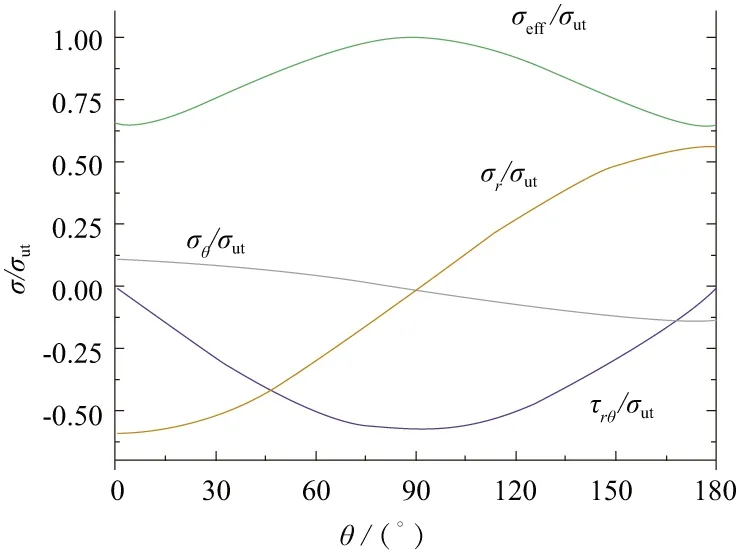
圖2 內徑處應力曲線

2 內聚力模型

對于彈塑性材料，使用梯形內聚力模型可有效描述其本構關系，但梯形內聚力模型計算收斂困難，故本文采用簡單有效的雙線性內聚力模型。

內聚力是描述物質原子或分子之間的相互作用力。內聚力模型實質是將材料的應力-應變曲線用牽引力-張開位移曲線來替代，如圖3所示，具體關系見式(5)。

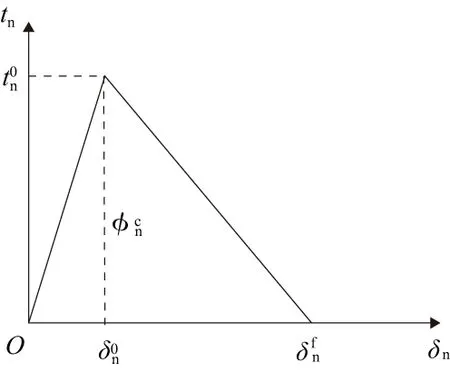
圖3 張開型雙線性內聚力模型

(5)

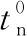
(6)

雙線性內聚力模型描述裂紋萌生至擴展可以分成3個階段(圖3)：

內聚力模型的張力位移關系及其特征參數可通過理論、實驗和計算獲得。例如，SQRENSEN B F與JACOBSEN T K[16]采用J積分法得到了雙層懸臂梁試件的張力位移關系。一般而言，雙線性內聚力模型參數可初步確定如下：1)內聚力剛度應大于材料彈性模量；2)內聚力強度取材料的屈服極限；3)內聚能等于J積分或根據斷裂韌度確定。

3 內聚力模型驗證

針對SAKATA M等人[17]研究的4340高強度鋼輪盤，根據基于內聚力模型的輪盤破裂轉速預測方法，利用有限元軟件ABAQUS預測破裂轉速。

輪盤幾何尺寸：內徑為30mm，外徑為150mm，初始徑向裂紋尺寸為a，外徑與內徑之差為W，且a/W=0.2，輪盤幾何模型示意圖如圖4所示。

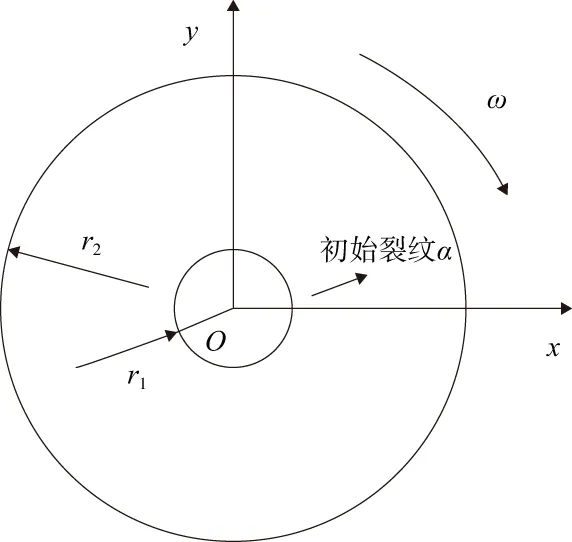
圖4 旋轉輪盤幾何模型

(7)

表1 4340內聚力模型特征參數

有限元模型：旋轉輪盤的單元類型為四節點平面應變減縮積分單元(CPE4R)，采用自由網格劃分技術。此外，在初始徑向裂紋沿徑向布置一層二維四節點內聚力單元(COH2D4)，其中初始裂紋擴展路徑上采用四邊形掃掠網格，指定掃掠方向沿內聚力單元厚度方向。有限元網格局部加密區域的網格尺寸，由下列公式確定：

內聚力區長度lcz[19]：

(8)

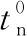
(9)

式中le為內聚力單元長度。

J積分隨單元尺寸變化的關系曲線如圖5所示，當單元尺寸<0.02mm時，J積分趨于常數。因此，單元尺寸選為0.02mm。

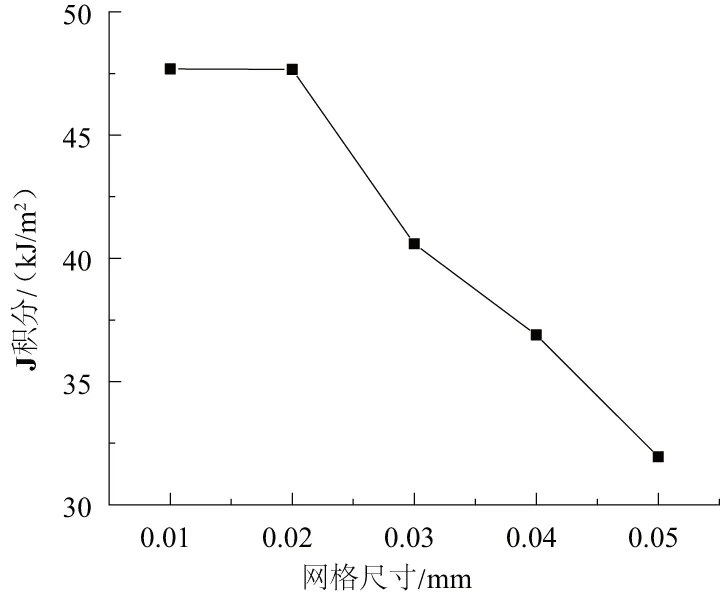
圖5 J積分與內聚力單元長度關系曲線

有限元網格示意圖如圖6所示，劃分了62311個四節點平面應變減縮積分單元、4800個二維四節點內聚力單元。

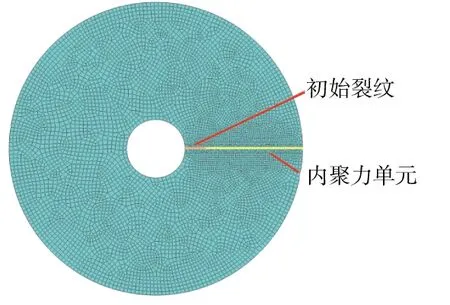
圖6 旋轉輪盤有限元模型(4340鋼)

施加載荷約束：為保證裂紋完全擴展，首先施加一個較高轉速，旋轉輪盤的角速度為38197r/min。

預測破裂轉速：若裂紋擴展至輪盤外邊界(圖7)，則輪盤破裂，此時對應的轉速即為破裂轉速。與文獻[17]中實驗獲得的破裂轉速相比，理論解的相對誤差為0.65%，內聚力解的相對誤差為2.51%，如表2所示。

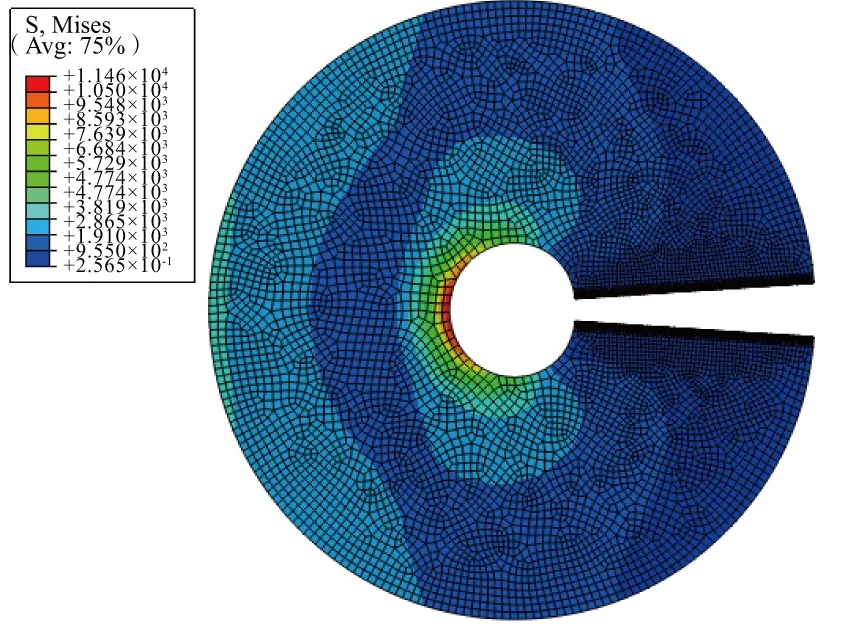
圖7 旋轉輪盤Mises應力云圖

表2 輪盤破裂轉速對比

4 內聚力模型應用

4.1 有限元計算

本節討論基于內聚力模型的GH4169輪盤的破裂轉速預測。破裂轉速計算步驟如下：

1) 輪盤幾何模型：內徑為25mm，外徑為100mm，初始徑向裂紋尺寸為0.5mm～2.5mm。

2) 定義材料參數：旋轉輪盤材料為GH4169，具體材料參數如下[20]：密度為8240kg/m3；彈性模量為162.0GPa；泊松比為0.330；屈服極限為976MPa；強度極限為1210MPa；J積分為45kJ/m2。根據旋轉輪盤材料參數，內聚力模型特征參數如表3所示。

表3 GH4169內聚力模型特征參數

3) 旋轉輪盤劃分了49049個四節點平面應變減縮積分單元(CPE4R)、3725個二維四節點內聚力單元(COH2D4)如圖8所示。

4) 施加載荷約束：旋轉輪盤的角速度為ω=57296r/min，內邊界上無約束。

圖8 旋轉輪盤有限元模型(GH4169)

4.2 有限元結果及分析

由圖9可知，旋轉輪盤的破裂轉速隨初始徑向裂紋尺寸增加而減小，且內聚力解相對于理論解誤差在4%以內。理論解均高于內聚力解，這是因為內聚力解模擬了裂紋擴展。

圖9 破裂轉速與初始徑向裂紋尺寸關系曲線

4.3 內聚力模型的參數影響

內聚力剛度與內聚力強度控制內聚力單元的線彈性階段與損傷起始點，內聚能確定內聚力單元的失效。內聚力模型的3個特征參數數量級相差較大，故考慮破裂轉速與3個參數變化百分比關系，如圖10所示，破裂轉速隨內聚力剛度、內聚力強度和內聚能增加而增加。內聚力強度的變化對破裂轉速影響最大。

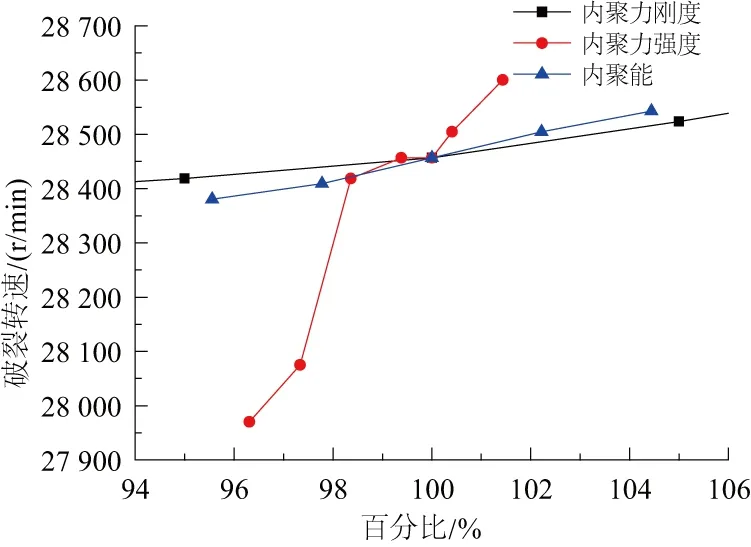
圖10 破裂轉速與內聚力剛度、內聚力強度、內聚能百分比關系曲線

5 結語

1) 基于雙線性內聚力模型研究含初始徑向裂紋的輪盤破裂轉速。該模型用于模擬含初始裂紋的輪盤裂紋擴展過程，并預測輪盤的破裂轉速。內聚力模型通過高強度鋼4340輪盤驗證，其預測的破裂轉速與實驗值相比誤差為2.51%。

2) 將內聚力模型應用于GH4169高溫合金輪盤。結果表明：隨著初始徑向裂紋尺寸的增加，破裂轉速下降；預測的破裂轉速與理論解相比誤差均<4%。

3) 內聚力模型中的內聚力強度參數對破裂轉速影響最大。因此，合理選擇內聚力模型中的強度特征參數可以提高模擬結果的準確性。