基于GA-PSO的地磚鋪設機器人作業點優化

張帥，陳柏 ，鞠鋒，席萬強

(1. 南京航空航天大學 機電學院，江蘇 南京 210016； 2. 南京信息工程大學 濱江學院，江蘇 無錫 214000)

0 引言

近年來，隨著經濟建設水平的不斷提高，建筑行業正在持續高速發展。然而隨著我國老齡化的不斷加重，造成了眼下的建筑行業勞動力短缺、勞動生產率低下等問題[1]。為了打破這種困局，大力發展建筑機器人以改變傳統作業模式勢在必行。而地磚鋪設作為房屋、樓宇建造中不可或缺的部分，基于當前的機器人技術，發展應用于地磚鋪設作業的機器人是很有必要的[2]。

通常，應用于地磚鋪設的建筑機器人是由地面移動模塊(如移動小車)以及空間作業的機械臂組成，亦可稱為移動機械臂，其作業方式是由兩個獨立的運動模塊協調完成的，因而如何規劃移動小車與機械臂的運動完成指定的任務是很重要的[3]。一般情況下，移動小車是先行駛到靠近目標點的位置停下，然后位于小車上的機械臂進行后續作業。國內外學者針對移動機械臂作業路徑規劃問題，展開了相關研究。

然而，在移動小車路徑規劃中，作業點的選擇，目前還沒有相關的研究。本文將針對此問題，研究使機械臂獲得最高靈活性，旨在得到移動機器人最佳的作業點位姿。文中主要介紹靈巧度和遺傳粒子群混合算法；描述了地磚鋪設機器人作業過程；以機械臂最大可操作度為目標，優化了移動小車的作業點位姿，并做了相關仿真驗證。

1 靈巧度分析

地磚鋪設移動機器人由移動小車和機械臂組成，如圖1所示。

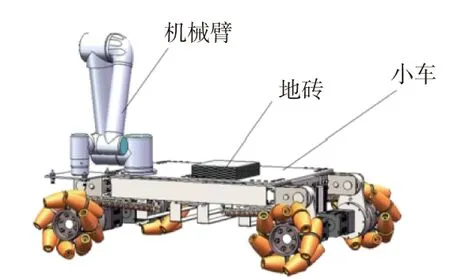
圖1 地磚鋪設機器人

在進行作業任務規劃時，移動小車作業點的位姿將會影響機械臂的作業性能。本文將以地磚鋪設移動機器人機械臂的靈巧度為優化指標，采用智能搜索算法，以確定移動小車最優的作業點。

1.1 可操作度

在串聯機器人中，描述機器人靈活度的運動靜力學性能指標，普遍使用YOSHIKAWA T[4]提出的可操作度指標，即

(1)

式中：J(q)為機器人的雅可比矩陣；JT(q)為雅可比矩陣的轉置。

由矩陣的J(q)奇異值，可操作度可寫為

ω=σ1，σ2，…，σm

(2)

可操作度ω反映了機器人在某一形位下各方向運動能力的綜合度量，用于衡量機器人的整體靈活性。在機器人進行作業時，可操作度值越大，機器人的靈活性就越好。當ω的值為0時，表明機器人處于奇異形位，應盡量避免這種情況的發生。

1.2 可操作度優化函數

地磚鋪設移動機器人在作業時作業點的位姿是以機械臂具有最大的操作靈活性為原則進行優化選擇的。可操作度的適應度函數表示為

(3)

式中ω為可操作度值。

2 地磚鋪設機器人作業步驟

地磚鋪設機器人的兩運動模塊協調作業時，移動小車作業點位姿的好壞將直接影響機械臂的操作靈活性，所以選擇合理的作業點是有必要的。

本文所提出的方法是以機器人靈活性最大為優化目標，在地磚鋪設作業范圍內選取一個合適的作業點。

圖2為地磚鋪設機器人作業示意圖。該系統由1個平面移動小車以及1個6自由度串聯機器人構成。具體步驟如下：移動小車停靠在機械臂的工作空間滿足貼磚作業要求的位置，機械臂從初始狀態運動至地磚正上方5cm處，如圖2(a)；機械臂末端手爪(吸盤)向下運行至最上方地磚并吸附，如圖2(b)；機械臂末端手爪運行至地面需貼合地磚區域的正上方5cm處，如圖2(c)；機械臂末端手抓向下運行直至地轉與地面貼合，如圖2(d)。至此完成了一個地磚的貼合過程；機械臂回歸到狀態圖2(a)，小車沿著貼磚路線運行至下一個作業點，開始新一輪的貼磚過程。

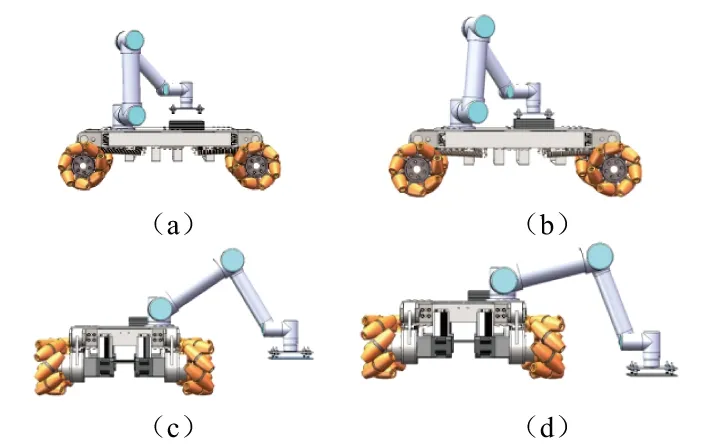
圖2 作業示意圖

3 GA-PSO混合算法

本文結合GA和PSO的優點，采用遺傳粒子群混合算法(GA-PSO)對地磚鋪設機器人的工作點位置進行優化，以能快速準確地得到作業點最優解。算法前期，依靠GA的交叉變異能力，全局探索以保證種群個體的多樣性，提供初步的優化結果，保留全局搜索的優勢。算法運行后期轉為執行PSO，強化局部搜索，提高收斂速度和計算精度[5]。圖3為GA-PSO算法流程圖。

具體的步驟如下：

1) 設置算法各參數值，并初始化種群信息，包括群體的規模N和維數D，每個粒子的位置xij和速度vij；

2) 計算種群中個體適應度值，確定當前種群最優位置Pi以及全局最優位置Pg；

3) 對種群中的個體進行選擇、交叉和變異操作；

4) 重復步驟3)，直到新種群個體數與設定的種群數相等，形成新的子種群；

5) 判斷是否滿足遺傳算法收斂條件。若不滿足則返回步驟2)；若滿足，則進行下一步操作；

6) 將經過GA操作后生成的種群作為PSO的初始種群；

7) 計算種群適應度，更新Pi和Pg的值；

8) 根據式(4)和式(5)更新粒子速度和位置；

vij(T+1)=ω·vij(T)+c1·rand(0,1)·

[pij(T)-xij(T)]+c2·rand(0,1)·[pgj(T)-xij(T)]

(4)

xij(T+1)=xij(T)+vij(T+1)

(5)

式中：ω為慣性因子；c1、c2為加速因子，值為正常數；

9) 判斷是否滿足終止條件，若滿足，則輸出最優解并結束計算，否則返回步驟7)。

GA與PSO運行次數比需要不斷調整，以便算法具有較高的搜索效率和精度。下面將運用GA-PSO混合算法優化地磚鋪設機器人工作點位置。

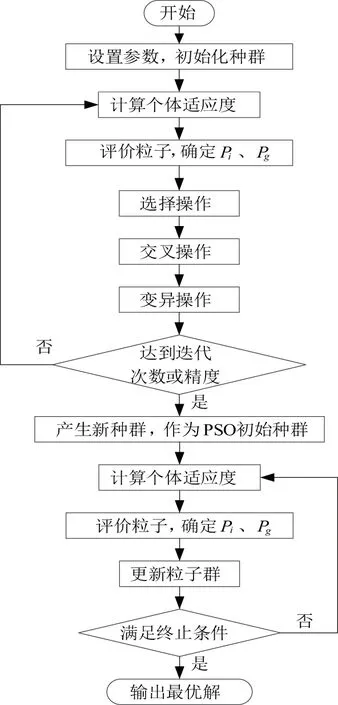
圖3 GA-PSO算法流程圖

4 實驗仿真

設定地磚鋪設機器人6-DOF串聯機械臂的連桿參數如表1所示，對應的空間初始狀態如圖4所示。

表1 6自由度串聯機器人連桿參數

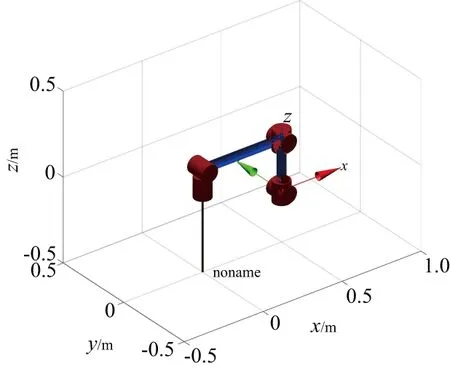
圖4 6自由度串聯機器人初始狀態

因地面需貼合地磚的位姿是固定不變的，移動小車的移動范圍不能過大，否則可能導致超出機械臂的作業范圍。因此，有必要建立6自由度機械臂的工作空間。設定各關節角的變化范圍為(-π,π)，采用迭代法得出機械臂的工作空間如圖5所示。

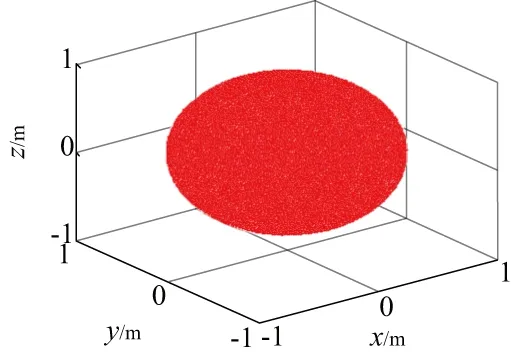
圖5 機械臂工作空間

考慮到機械臂末端手爪最后貼磚是與地面處于同一水平線，因此需要給出機械臂工作空間z=d時xy平面的作業范圍，其中d為小車車身的高度與機械臂第1個關節的高度之和。設定機械臂中心點與移動小車上地磚中心點的距離為0.3m；小車車身高度為0.3m，如圖6所示。

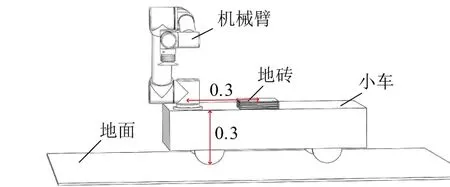
圖6 貼磚機器人參數值示意圖

對圖5工作空間取z=-0.4m的截面，即為機械臂末端手爪在地面的運動范圍，如圖7所示。由圖可知，機械臂末端手爪在地面的作業范圍為半徑0.6m的圓。

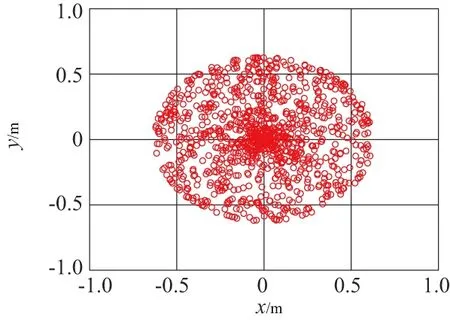
圖7 機械臂在地面的作業范圍

建立地磚鋪設機器人地面坐標系統，簡圖如圖8所示。綠色方塊為貼磚的位置；黃色區域為移動小車的移動范圍(因本刊為黑白印刷，有疑問之處可咨詢作者)由圖可知，坐標點(-0.5,0.3)m距離原點最遠，其距離值為0.583m，<0.6m，是滿足機械臂地面作業范圍要求的。

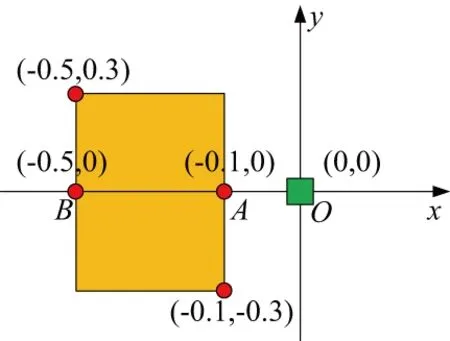
圖8 貼磚移動機器人作業停靠點坐標系簡圖

任務要求：移動小車在長0.6m，寬0.4m的矩形區域內選擇作業點，使得機械臂鋪磚作業時的可操作度最大。需要指出的是，由于磚塊的形狀并不是圓形，一般為正方形或矩形，因此機械臂在作業時應保持其末端姿態不變。

上述可操作度優化目標的數學形式描述如下：

(6)

式中fω(x,y)為可操作度優化函數。

由于在地磚鋪設前3步驟中，機械臂每次都會執行這一相同過程，作業點位姿的變化并不會帶來可操作度值的變化，因而可省略；而后3步驟中移動小車作業點位姿的改變將帶來機械臂作業過程中可操作度的變化，并且由于第6步驟與4、5兩步驟重復；所以只需計算4、5兩步驟的可操作度即可。

基于上一小節提出的GA-PSO混合算法對移動小車的停靠位置進行優化。

優化結果如下：

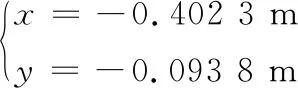
(7)

對應的最大可操作度值為0.0375m。圖9列出了小車在黃色區域范圍內，機械臂的可操作度散點圖，不同的顏色表示不同的數值大小，其中藍色程度越深表示可操作度值越小，黃色程度越深表示可操作度值越大。由圖9可知，可操作度值較大的區域主要分布在點(-0.4,-0.1)附近。需要指出的是，在下一輪的鋪磚作業過程中，不需要重新計算機械臂作業的可操作度值，移動小車的最優作業點依然為新的貼磚位置為原點的(-0.402 3,-0.093 8)坐標點處。

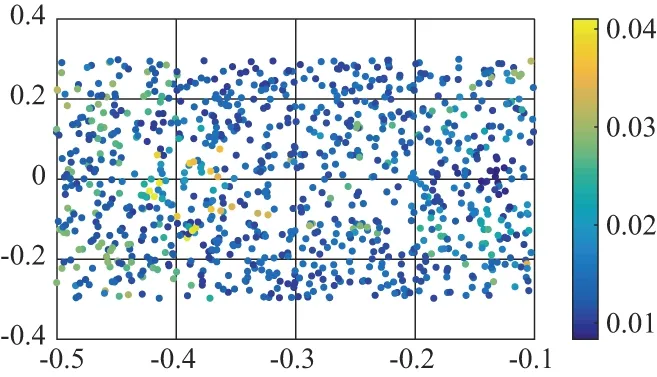
圖9 可操作度散點色條圖

5 結語

本文針對建筑移動機器人地磚鋪設過程中，移動小車作業點選擇問題進行了較為深入的研究。以最大可操作度為優化指標，并利用GA-PSO混合算法優越的搜索性能，優化移動小車進行鋪磚作業時的作業點，以保證機械臂的操作靈活性。為驗證所提方法的有效性，本章利用MATLAB編寫仿真程序，最終得到了機械臂的可操作度在移動小車位于不同作業點時的平面分布圖，并通過GA-PSO混合算法得出了移動小車的作業點位于坐標為(-0.4023,-0.0938)的點處，其可操作度值最大。相關仿真結果表明，本文所提出的基于GA-PSO混合算法的可操作度優化方法可以精確地得到移動小車的作業點，解決了移動小車與機械臂協調作業時路徑規劃的難題。