從幾道高考題談有界磁場的臨界與極值問題的數理方法

胡衛雄

(湖北省武漢市常青第一中學 430000)

在研究帶電粒子在洛倫茲力作用下的圓周運動時，經常會遇到粒子通過有界磁場區域的運動情形，往往因為初始速度不同，所處的磁場磁感強度大小不定，運動圓軌跡在變化，同時由于邊界的約束從而產生 “恰好”“最大”“至少”等臨界與極值問題，本文以幾道高考題為例，分類討論通過帶電粒子在有界磁場運動的的臨界極值問題的數理分析方法.

一、帶電粒子恰好不穿出磁場區域的臨界問題

當帶電粒子通過有界磁場區域時，如果帶電粒子的初始速度不同，所處的磁場磁感強度大小不定，運動圓軌跡在變化，由于邊界的約束從而產生“恰好”不穿出磁場區域的臨界情形，此類問題一般需要推理出帶電粒子恰好不穿出磁場區域的臨界條件(在磁場中運動的軌跡與邊界相切)，畫出臨界條件下的的運動軌跡圖，應用“臨界軌跡+幾何關系”，結合帶電粒子在洛倫茲力作用下的圓周運動的物理規律列方程聯立求解．

例1 (2020·全國卷Ⅲ第18題)真空中有一勻強磁場，磁場邊界為兩個半徑分別為a和3a的同軸圓柱面，磁場的方向與圓柱軸線平行，其橫截面如圖1所示.一速率為v的電子從圓心沿半徑方向進入磁場.已知電子質量為m，電荷量為e，忽略重力.為使該電子的運動被限制在圖中實線圓圍成的區域內，磁場的磁感應強度最小為( ).

答案：C

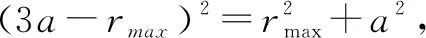
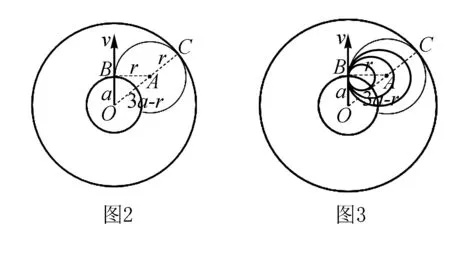
點評本題中，電子的速度大小恒定為v,方向確定為沿半徑方向，因為磁感強度大小不確定，運動半徑不確定.以入射點B為定點，圓心位于與初速度垂直的同一直線BA上，將半徑放縮作軌跡，作出一組如圖3所示的半徑逐漸增大的“縮放圓”.分析中，重點在于利用放縮的動態軌跡圓，找出臨界條件下(與半徑為3a的圓柱面相切)的“臨界軌跡”，分析臨界條件下的幾何關系，結合帶電粒子在磁場中圓周運動的動力學規律求解.

二、帶電粒子在有界磁場中運動時間的極值問題

當帶電粒子通過有界磁場區域時，如果帶電粒子的初始速度不同，運動圓半徑不同，運動圓軌跡在變化，由于邊界的約束，各粒子在磁場中運動的時間長短不一樣，從而產生粒子在有界磁場中運動時間的極值求解問題.如果磁場的磁感強度恒定，帶電粒子的荷質比相同，各粒子在磁場中運動的周期相同，則可根據圓心角判斷時間的極值：粒子運動轉過的圓心角越大，時間越長．此類問題一般需要推理出帶電粒子在有界磁場中運動時間的極值條件(圓心角最大)，畫出極值條件下的的運動軌跡圖， 應用“極值軌跡+幾何關系”，結合物理規律求解.如果不容易畫出極值條件下的運動軌跡圖，則可應用“一般軌跡+幾何關系”，得到相關物理量之間的函數關系，通過數學方法求極值條件，再結合物理規律求解.

例2 (2020·全國卷Ⅰ第18題)一勻強磁場的磁感應強度大小為B，方向垂直于紙面向外，其邊界如圖4中虛線所示，ab為半圓，ac、bd與直徑ab共線，ac間的距離等于半圓的半徑.一束質量為m、電荷量為q(q>0)的粒子，在紙面內從c點垂直于ac射入磁場，這些粒子具有各種速率.不計粒子之間的相互作用.在磁場中運動時間最長的粒子，其運動時間為( ).

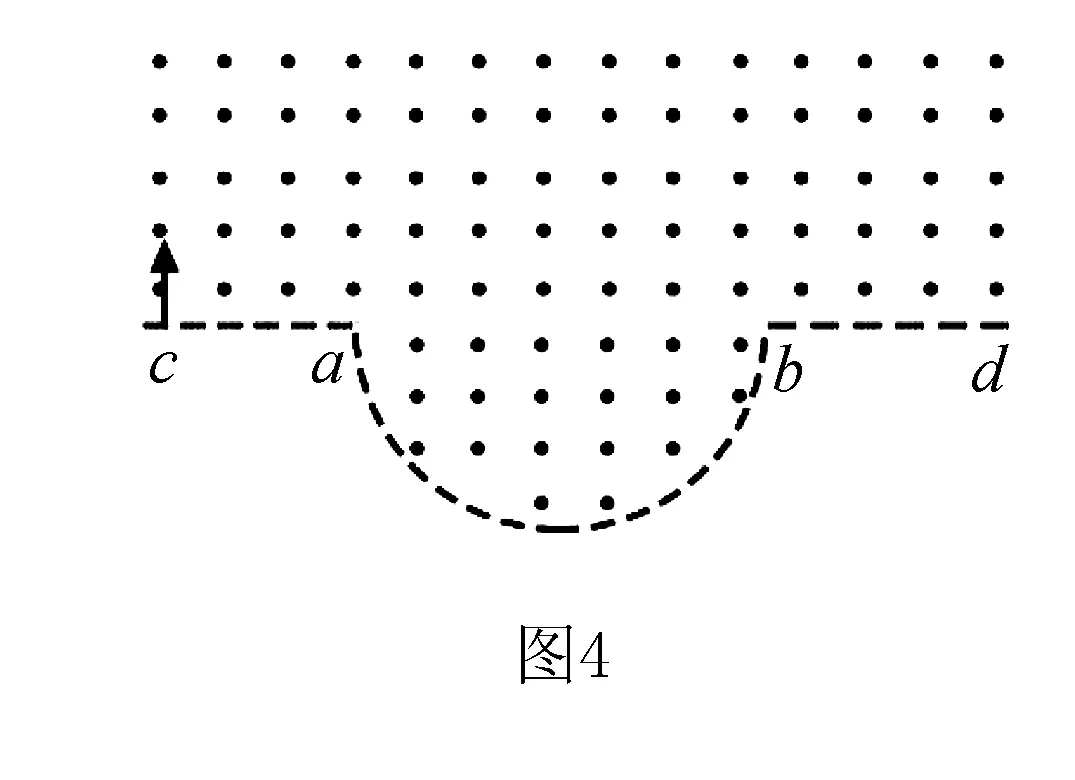
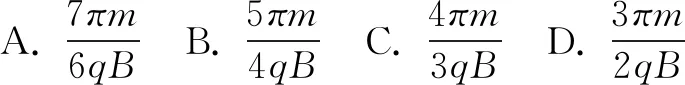
答案：C

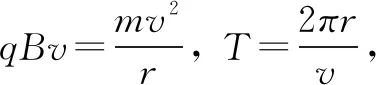
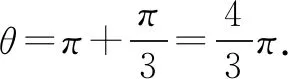
方法二：采用“一般軌跡+幾何關系”，利用數學函數關系求極值解決該問題.假設粒子運動軌跡如圖6所示,圓心在O點，ab半圓的圓心在O′，OO′=2R-r,Oe=r,O′e=R,由余弦定理有

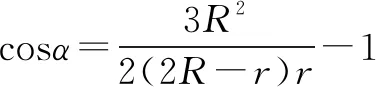
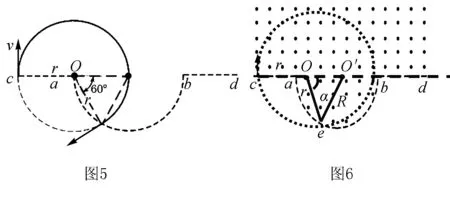
點評本題中，勻強磁場的磁感應強度恒定，一束粒子的電荷量，質量相同，速度方向相同，速率大小不同，他們的軌跡組成一組半徑逐漸增大的縮放圓.方法一當半徑r≤0.5R和r≥1.5R時，粒子分別從ac、bd區域射出，磁場中的軌跡為半圓，運動時間等于半個周期.當0.5R

三、帶電粒子穿出磁場時打在在磁場邊界區域范圍

當帶電粒子通過有界磁場區域時，如果帶電粒子的初始速度不同或者磁感應強度大小不定，則各粒子在磁場中運動的軌跡不同，由于邊界(或極板/熒光屏)的約束，一部分粒子打在邊界(或極板/熒光屏)上，從而產生粒子穿出磁場時打在在磁場邊界區域范圍的求解問題.此類問題一般需要推理出帶電粒子穿出磁場時打在在磁場邊界上距離最遠的極值條件(軌跡與邊界相切或打在邊界時軌跡對應的弦長最長)，畫出極值條件下的的運動軌跡圖， 應用“極值軌跡+幾何關系”，結合物理規律求解．也可選取一般情形，畫出軌跡圖，結合幾何關系，列出相關物理量之間的函數關系，通過數學方法求極值.

例題3 (多選)(2015·四川高考)如圖7所示，S處有一電子源，可向紙面內任意方向發射電子，平板MN垂直于紙面，在紙面內的長度L=9.1 cm，中點O與S間的距離d=4.55 cm，MN與SO直線的夾角為θ，板所在平面有電子源的一側區域有方向垂直于紙面向外的勻強磁場，磁感應強度B=2.0×10-4T，電子質量m=9.1×10-31kg，電量e=-1.6×10-19C，不計電子重力，電子源發射速度v=1.6×106m/s的一個電子，該電子打在板上可能位置的區域的長度為l，則( ).

A．θ=90°時，l=9.1 cm B．θ=60°時，l=9.1 cm

C．θ=45°時，l=4.55 cm D．θ=30°時，l=4.55 cm

答案：AD

方法一：分別畫出四種對應情況下的極值軌跡圖，結合幾何關系求解極值條件.θ=90°時，擊中板的范圍如圖9甲，電子軌道正好與MN相切于M點，l=2R=9.1 cm，選項A正確；θ=60°時，擊中板的范圍如圖9乙所示，臨界情況電子軌道正好與MN相切，但切點在OM之間，l<2R=9.1 cm，選項B錯誤；θ=30°，如圖9丙所示，顯然臨界情況電子軌道與MN相切，切點正好與O點重合，l=R=4.55 cm，當θ=45°時，擊中板的范圍如圖9丁所示，顯然臨界情況電子軌道與MN相切于切點，在OM之間，l>R(R=4.55 cm)，故選項D正確，選項C錯誤.

點評本題中，應為入射點的位置在發生變化，對應四個選項中，SO與MN的夾角各不相同，方法一要分別分析四種情形下的“極值軌跡+幾何關系“，應用方法二只需析一種情形下的極值和幾何關系，不過方法二對幾何關系的分析和三角函數知識要求較高，具體問題中還需要根據實際情況選擇合適的解決方法.

綜上所述，帶電粒子在有界磁場的臨界極值問題，需要挖掘隱含條件、分析臨界狀態、確定極值條件、明了幾何關系、結合數學知識、運用物理規律，對空間想象能力、推理分析能力要求較高.在分析過程中，對應相關的問題模型，可以利用動態的運動軌跡，采用“臨界或極值軌跡+幾何關系”，探索臨界與極值條件，結合物理規律解決問題；也可以采用“一般軌跡+幾何關系”，推理相關物理量的函數關系，利用數學知識求解臨界極值條件，結合物理規律求解.