基于基因表達式編程算法的波浪透射預測

劉 濤，馮 曦，馮衛兵，張宸豪，陸 楊

(1. 海岸災害及防護教育部重點實驗室(河海大學)，江蘇 南京 210098； 2. 河海大學 港口海岸與近海工程學院，江蘇 南京 210098； 3. 南京水利科學研究院，江蘇 南京 210029)

波浪透射預測是海洋工程中的一項基礎性研究，它對于維護港口水域平穩、船舶穩定以及海岸泥沙輸移等有著深遠影響。因此，準確預測波浪透射對于海洋工程極其重要。

大型深水防波堤堤后波浪一般來自兩個方面，其一是堤頂越浪，其二則是堤身滲透波浪。針對越浪的情況，國內外學者已經做了大量的研究[1-4]，得到的成果可以很好地應用到實際工程中。但是對于不可越浪的防波堤透浪研究，國內外的成果相對較少。

波浪透射的程度，通常用透浪系數來表述，其定義如下：

Kt=Ht/H

(1)

式中：Kt為透浪系數，Ht為堤后波高，H為入射波高。透浪系數的大小反映了波浪在堤內的衰減程度，Kt越小，衰減越顯著。目前研究波浪透射主要從理論推導和物理模型試驗兩種方法入手。理論研究方面，Sollitt和Cross[5]假設拋石斜坡堤的斷面是矩形結構，忽略了黏性項和對流項的影響，利用數學推導得到波浪透射系數的解析解，此后國內外學者開始關注波浪與多孔介質相互作用的問題。Madsen[6]利用線性波理論得到波浪在堤內的衰減公式。Stephenson[7]假定水頭損失處在阻力平方區，推導出半理論半經驗計算公式，得到的結果通過試驗數據驗證較為滿意。

物理模型試驗方面，王登婷和左其華[8]、葛曉丹[9]和Sokolewicz[10]等做了大量的物模試驗，闡明了影響波浪透射的因素主要分為兩方面：一方面是波浪本身的特性，比如波高、波周期和波陡等；另一方面由防波堤的結構決定，堤寬、中值粒徑和堤前水深等均有較大影響。

以上學者的研究都帶有一定的局限性，理論推導需要簡化模型，而物模試驗又受限于比尺效應，致使提出的公式只能應用在一個限定的范圍內。近年來，隨著人工智能技術，如遺傳算法、人工神經網絡和基因表達式編程(gene expression programming, 簡稱GEP)算法等被引進海洋工程，極大地促進了這些學科的發展。Deo和Jagdale[11]，Jain和Deo[12]利用人工神經網絡來模擬波浪的傳播；Robertson等[13]將GEP算法運用到波浪破碎問題中，解決了近海波浪破碎條件難以精準預測的問題；Ebtehaj和Bonakdari[14]采用GEP算法模擬泥沙運輸；Power等[15]利用GEP算法來預測波浪爬高，均取得了不錯的進展。

針對傳統研究方法較難準確預測波浪透射的問題，采用GEP算法預測規則波作用下不越浪防波堤的波浪透射系數，研究GEP算法預測精度隨訓練組數變化的規律，比較GEP算法與各家經驗公式的優劣，并通過對各影響變量進行敏感性分析，確定影響波浪透射的最顯著因素。

1 試驗數據

數據是GEP算法運行的基礎，精準評估各家透浪系數計算公式也要更多詳細數據的支撐。開展的物理模型試驗在水槽中進行，水槽尺寸為90 m×0.5 m×1.0 m(長×寬×高)。試驗采用規則波，試驗布置如圖1所示。入射波是由水槽前端推板式造波機生成，水槽末端設置斜坡式消浪板進行消浪，有效減小波浪反射的影響。波高是通過布置在防波堤前后的四根浪高儀來采集，浪高儀采用DJ800,采集頻率為50 Hz。防波堤坡度為1∶1.5，護面型式采用單層扭王字塊，單個扭王重370 g，堤心石采用有棱碎石，粒徑變化范圍為0.008～0.032 m。

此外，為了提高GEP算法的預測能力和評估各家公式的精準度，本次研究還收集了前人的試驗數據，形成一個龐大的透浪試驗數據庫，共計567組，代表了各種波浪條件(0.002 m≤H≤0.24 m，0.71 s≤T≤7 s)。試驗水深的變化范圍是0.2 m≤d≤0.5 m，涵蓋實驗室水槽大部分水深情況。靜水面堤寬是影響波浪透射的重要因素，堤寬最小只有0.08 m，最寬達到1.7 m。堤身中值粒徑的變化范圍0.013 m≤D50≤0.055 m。表1為文中用到的試驗數據。

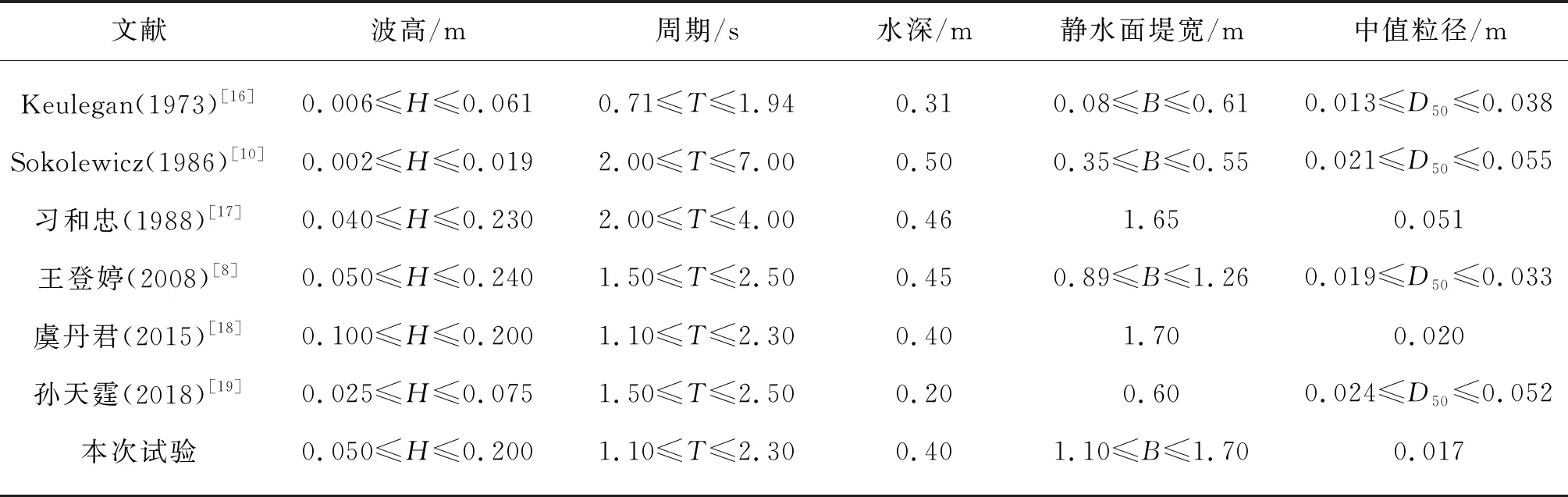
表1 試驗數據

2 研究方法與內容

2.1 算法介紹

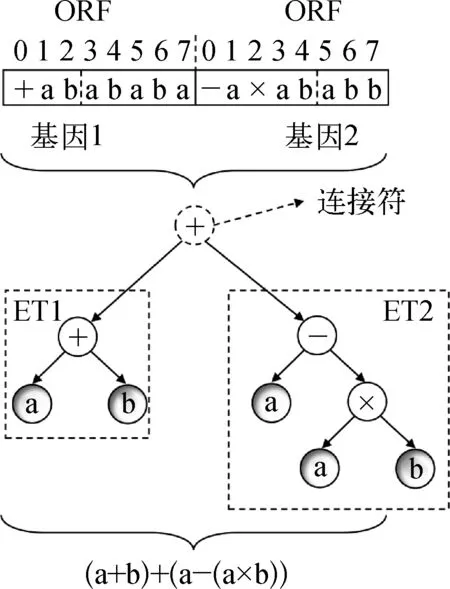
圖2 GEP染色體和表達式樹

基因表達式編程(GEP)算法是由Ferreira于2001年在遺傳算法和遺傳編程的基礎上提出來的，它既有遺傳算法“定長線性串”的簡單特性，也有遺傳編程“動態樹結構”的搜索能力[20]，是一種基于生物基因結構和功能發明的新型自適應演化算法。GEP算法通過模擬生物遺傳進化采用概率化的尋優方法，自適應調整搜索方向，極大地加快了收斂速度。如圖2所示，GEP算法借鑒了生物學的開放讀碼框架(ORF)概念，并且采用表達式樹(ET)來進行解碼，相較于其他遺傳算法，簡化了算法編碼，提升了計算效率。

GEP算法的進化流程：首先隨機給出一個初始化種群，然后通過ET來表達染色體，接著確定這個種群是否滿足預設的終止條件，終止條件一般選擇最大進化代數或計算精度。如果滿足，保留最優個體輸出。如果不滿足，則需要對這個種群采用一系列的遺傳操作算法，如變異、倒串、基因重組等等，形成一個新的種群，再接著上一輪的操作，直到滿足終止條件為止。

2.2 波浪透射預測的GEP算法

2.2.1 輸入變量

根據前人研究成果[6-10],入射波高(H)、波周期(T)、水深(d)、靜水面堤寬(B)和堤心石中值粒徑(D50)對于波浪透射影響較大。結合影響波浪透射的兩個方面：波浪特性和防波堤結構，對各影響變量進行無量綱化，考慮深水波陡(H/gT2)、相對波高(H/d)、相對堤寬(B/D50)和相對水深(d/L)對波浪透射的影響，設置了6組變量組合。比較不同組合情況下GEP算法對波浪透射的預測能力，確定最優組合，建立透浪系數表達式。表2是本次研究的GEP算法參數設置。

采用以下幾個統計參數作為評價指標：均方根誤差(RMSE)、標準均方差(NMSE)、決定系數(R2)和平均預測誤差(BIAS)。它們的計算如下：

(2)

(3)

(4)

(5)

RMSE和NMSE越小代表預測值越精確，R2越接近1表示預測效果越好，當BIAS為正數時表示預測值大于試驗值，BIAS為負數時表示預測值小于試驗值。

表2 GEP算法參數設置

2.2.2 輸入樣本數量

為了探究GEP算法的預測精度與輸入樣本數量之間的關系，將數據分成訓練組和驗證組，訓練組中的數據以50組為間隔逐漸增加，驗證組的數據用于比較不同組次對波浪透射的預測效果。定量評估不同組次的預測精度，除了式(2)～(5)幾個指標外，定義了“精度區間”，即預測理想值±2倍均方根誤差。為了方便統計，此處的均方根誤差采用統一值，即不同組次中均方根誤差的平均值。

2.3 透浪系數經驗公式

本次研究選取了兩家不越浪防波堤透浪系數計算公式，用于對比分析GEP算法的預測能力。

2.3.1 Madsen公式

Madsen[6]假定水頭損失與速度為線性，堤內是完全紊流狀態，利用線性波理論推導出波浪在堤內衰減狀況，公式如下：

(6)

式中：Kt為透浪系數，H為入射波高，B為堤身寬度，d為水深，β為恩格隆摩擦系數，

(7)

式中：n為孔隙率，D50為名義中值粒徑。

2.3.2 Stephenson公式

Stephenson[7]認為水流處在阻力平方區，水頭損失與速度平方成正比，通過理論推導并簡化，得到防波堤透浪系數計算公式：

(8)

式中：μ為阻力系數，一般是雷諾數和石頭形狀系數。Stephenson根據試驗結果歸納出μ的計算式：

(9)

式中：Re為雷諾數，μt為形狀系數，光滑球狀塊石μt=1，半圓礫石μt=2，有棱碎石μt=3。

3 結果分析與討論

3.1 最優輸入變量組合

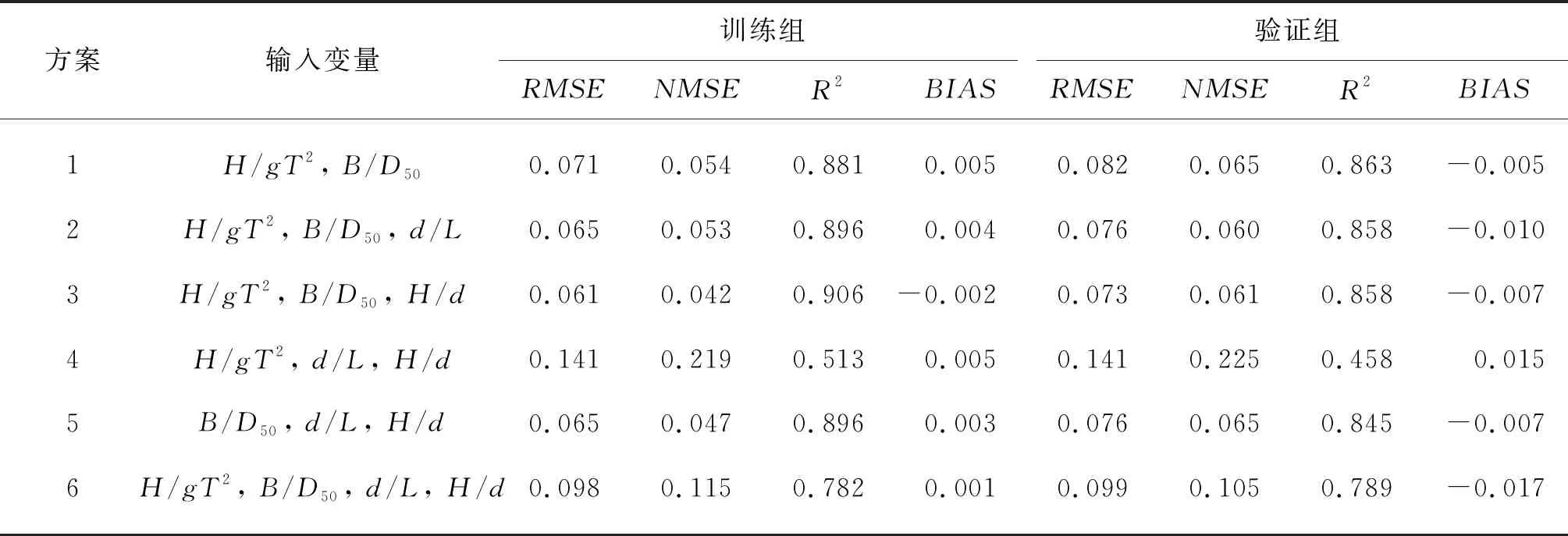
隨機地選擇80%的數據(454組)用于訓練，剩余20%的數據(113組)用于驗證，考慮深水波陡(H/gT2)、相對波高(H/d)、相對堤寬(B/D50)和相對水深(d/L)對波浪透射的影響。表3給出了不同方案的GEP算法對波浪透射預測效果的評價結果。方案4沒有考慮相對堤寬的影響，相對于其他方案預測精度較低，表明相對堤寬對于波浪透射影響較為顯著。方案6考慮了4個變量的影響，但是預測精度仍不及方案1、2、3和5。方案3中驗證組的表現優于其余方案，在未知試驗條件下預測精度最高，因此確定方案3作為GEP算法的最優輸入組合，建立的透浪系數計算公式：

(10)

3.2 輸入樣本數量對GEP算法預測精度的影響

選擇67組不同試驗條件下的透浪數據來驗證輸入樣本數量的變化對GEP算法預測精度的影響，結果如圖3所示。可以看出，當訓練組數較少時，GEP算法的預測精度不高，大部分數據處在“精度區間”外，且預測的精度隨著訓練組數的增加而提高。當訓練組數達到300組時，僅有少量數據處在“精度區間”外，說明此時GEP算法已具備較高的預測精度。隨著訓練組數的繼續增加，GEP算法的預測精度提升不大，精度逐漸趨于平穩。表4總結了不同訓練組數情況下驗證組數據的RMSE、R2和落入“精度區間”占比。不難看出，RMSE和R2的變化也呈現上述規律。

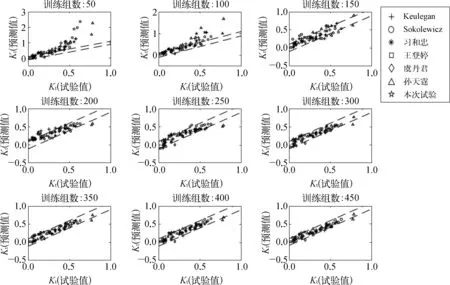
圖3 不同訓練組數的GEP算法對波浪透射的預測效果

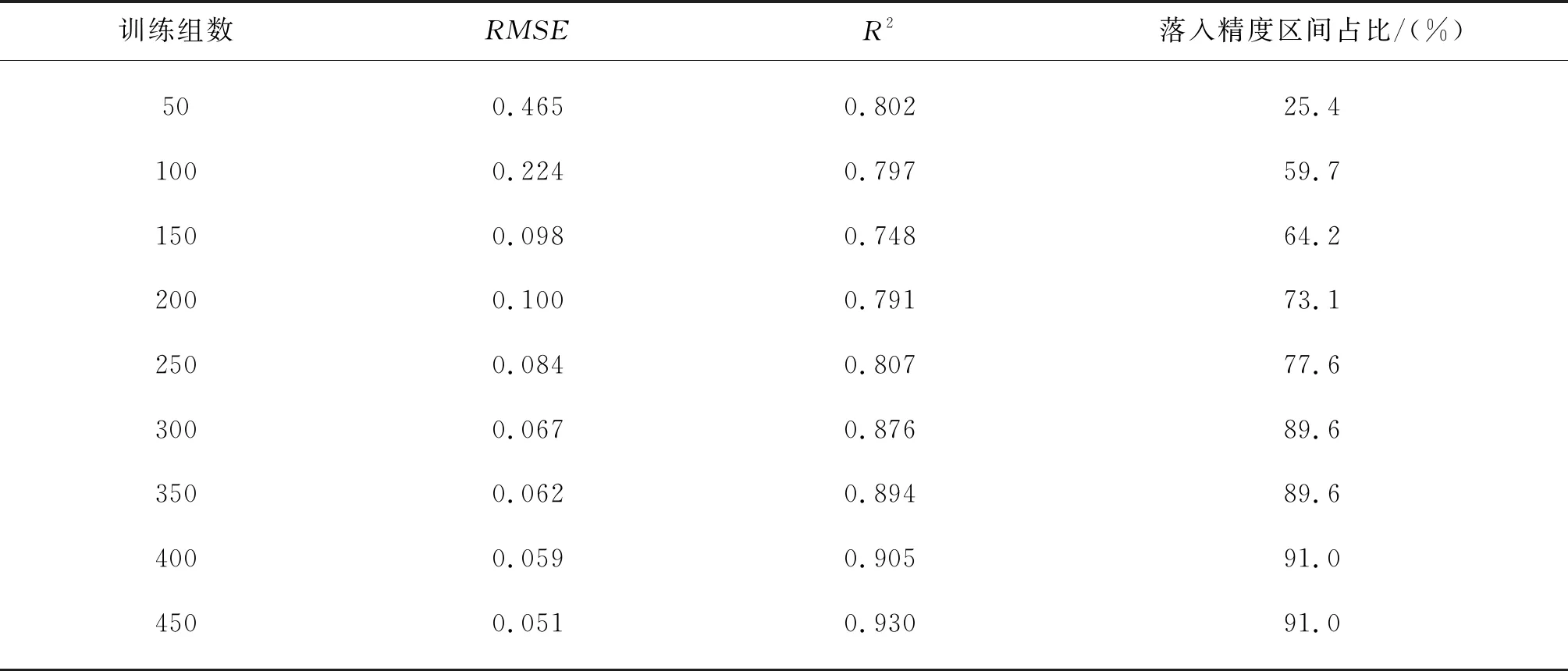
表4 不同訓練組數的GEP算法對波浪透射預測效果評價指標

3.3 兩家經驗公式和GEP算法的預測透浪效果比較

將GEP算法與兩家經驗公式對波浪透射的預測效果作比較，圖4和表5分別從定性和定量上給出了結果。從圖4中可以明顯看出，無論是訓練組還是驗證組，GEP算法對于透浪的預測精度大大高于兩家經驗公式。整體上Madsen公式的表現要優于Stephenson公式，但是Madsen公式在推導過程中沒有考慮波浪周期的影響，致使公式在周期較小的情況下預測結果偏差較大。Stephenson公式的預測值一般比試驗值大3～4倍，主要原因是公式在推導過程中將液體質點軌跡假設為圓形，但是實際防波堤多建于淺海，液體軌跡已經近似橢圓。由表5可知，GEP算法的所有評價指標相比以上兩家經驗公式均達到了最小值，其中驗證組的RMSE、NMSE和BIAS分別是0.073、0.061和-0.007，R2高達0.858，預測結果較好。

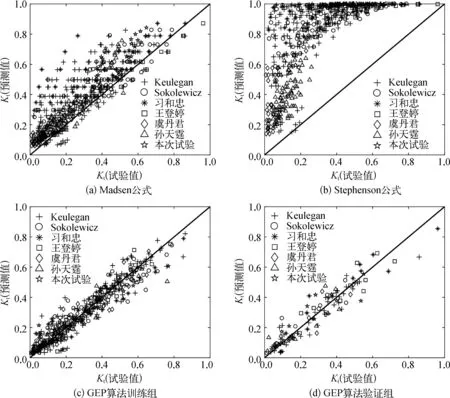
圖4 透浪試驗值和各家經驗公式及GEP算法預測值的比較

表5 各家經驗公式與GEP算法對波浪透射預測效果的評價指標

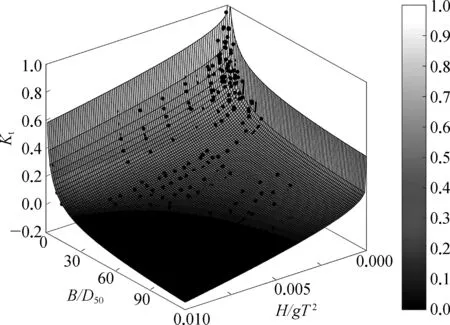
圖5 透浪系數隨深水波陡和相對堤寬的變化趨勢

考慮深水波陡和相對堤寬對波浪透射的影響，繪制透浪系數隨二者變化的三維圖，如圖5所示。圖上散點是試驗值，曲面是GEP算法預測值。由圖可知，GEP算法預測值與試驗值吻合良好。當H/gT2和B/D50較小時，Kt隨二者的增大而急劇減小，隨著H/gT2和B/D50的不斷增大，Kt的減小速度逐漸變緩。

3.4 敏感性分析

為了確定各輸入變量對波浪透射的影響程度，對每個變量進行敏感性分析。敏感性分析采用偏導數靈敏度分析法[21]，利用GEP算法得到的透浪系數顯式表達式，對各個變量求偏導，然后計算每一個變量對應的值。當縱坐標為負數，表明透浪系數隨變量的增大而減小，二者呈負相關；當縱坐標為正時，則相反，結果如圖6所示。從圖中可以看出三個輸入變量中深水波陡是影響波浪透射的最主要因素。透浪系數與深水波陡、相對堤寬和相對水深均呈負相關，即透浪系數隨著三者的增大而逐漸減小。三個輸入變量對透浪系數的影響均呈對數分布，表明變量數值越小波浪透射受其影響程度越大。

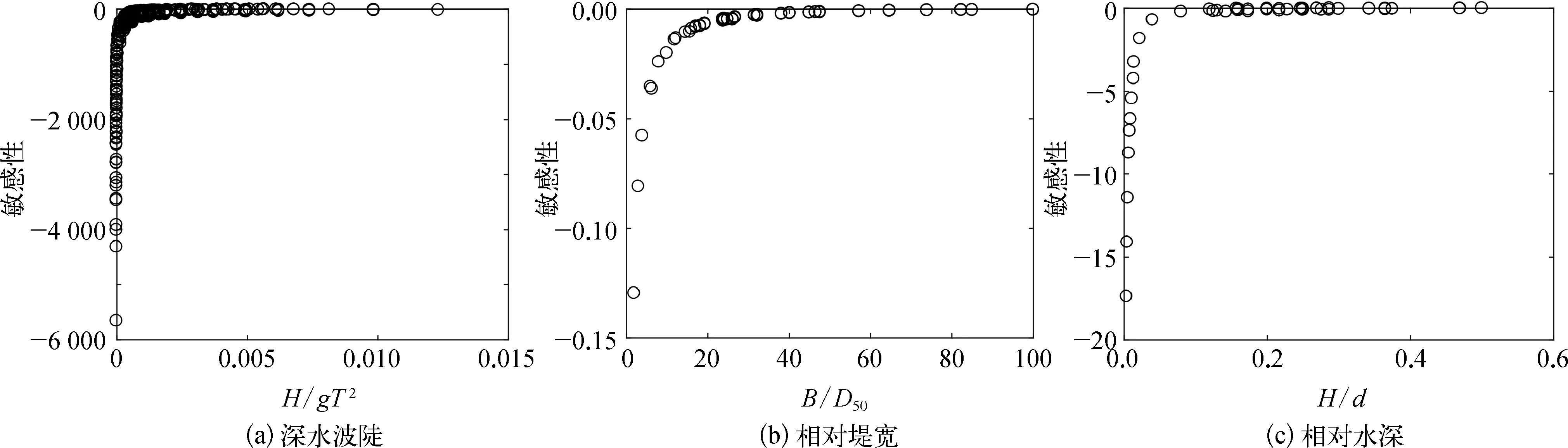
圖6 輸入變量敏感性分析

4 結 語

針對規則波作用下不越浪防波堤的波浪透射問題，基于567組透浪試驗數據，采用GEP算法預測波浪透射系數，確定了GEP算法的最優輸入變量組合并建立了透浪系數顯式表達式，研究了GEP算法預測精度的變化規律，主要結論如下：

1) 深水波陡、相對堤寬和相對波高是GEP算法預測波浪透射系數的最優輸入變量組合。

2) 當訓練數據較少時，GEP算法對波浪透射的預測精度不高，且預測精度隨著訓練數據的增加而提高。當訓練組數達到300組時，GEP算法已具備較高的預測精度，隨著訓練數據的繼續增加，預測精度提升不大。因此，后續的透浪研究工作者可以通過收集前人已做的300組試驗數據進行研究，可避免重復性的物理試驗。

3) GEP算法對波浪透射的預測精度遠遠高于前人的經驗公式，驗證組的RMSE、NMSE和BIAS分別是0.073、0.061和-0.007，R2高達0.858。GEP算法的敏感性分析結果表明，透浪系數隨著深水波陡、相對堤寬和相對水深的增加而減小，深水波陡相較于另外兩個輸入變量影響波浪透射效果更為顯著。