親油型聚結濾芯飽和度預測模型研究

常程，姬忠禮，劉佳霖

（1 中國石油大學（北京）石油工程學院，北京102249； 2 中國石油大學（北京）機械與儲運工程學院，過程流體過濾與分離技術北京市重點實驗室，北京102249）

引 言

纖維聚結濾芯在生產制造和過程工業中廣泛應用，主要作用是除去氣流中的液體氣溶膠顆粒[1]，以保障各工藝過程中核心動力設備的長周期安全運行。對于聚結過濾過程，液滴在濾材內部的運移情況較為復雜：液滴首先在擴散、攔截和碰撞等過濾機理作用下被纖維所捕獲，被捕獲的小液滴與后續來流中的液滴相互碰撞融合進而逐漸聚結長大，聚結后的液體隨氣流在多層濾材內運移至濾芯排氣側表面，最終液體在重力和氣體曳力作用下排出濾芯，實現氣液分離。過濾效率和壓降是聚結濾芯的關鍵性能評價指標，而這兩個指標明顯受到濾芯內液體含量及分布情況的影響。捕獲的液體將導致濾芯阻力增加以及效率降低，嚴重影響濾芯過濾性能。因此，研究聚結濾芯內液體捕獲、運移和分布情況具有重要意義。

Contal 等[2]在過濾過程中不同時刻對濾材內液體分布形態進行了觀測，當液體在纖維交接處相互橋連形成液橋和液池時，濾芯壓降將出現指數增長并伴隨液滴穿透量驟然升高。Kampa 等[3-4]分析了液體在親油及疏油型濾材表面及內部運移情況，提出了“跳躍-通道”模型，認為濾芯潤濕壓降由兩種液體運移機制所決定：當液體在濾材內部運移時，將沿著氣流方向形成多條平行的貫穿整個濾芯厚度的通道，由此產生通道壓降，此壓降與濾材厚度及液體載荷量呈正比；當液體排出親油型濾材或進入疏油型濾材時，在毛細作用力下產生跳躍壓降，此壓降不受操作條件影響而與濾材毛細特性相關，且跳躍壓降的出現伴隨著濾材表面液膜的形成。作者前期研究[5]表明，親油型聚結濾材排氣側表面形成的液膜是導致液滴二次夾帶和過濾效果明顯降低的主要原因。陳鋒等考查了孔徑梯度濾材內液體分布特征，發現濾材內存在液體運移通道傳遞現象，表明通過調整孔徑梯度可改變液體分布，進而提高濾材過濾性能[6]；進一步地，研究了液體表面張力對液體分布特性的影響，發現較高的表面張力使得通道數量減少并且單通道面積增大[7]。Kolb等[8]基于液體在濾芯內分布情況提出了新的效率計算模型，測定分析了首層濾材、通道區域及液膜對于總體過濾效率的貢獻程度。隨后，Penner等[9]研究發現，液體通道區域內增加濾材層數將導致總體穿透率的上升，而液膜的形成則會降低穿透率，且過濾速度是影響液膜穿透率的重要參數。此外，Kolb等[10]對聚結濾芯穩定階段出現的壓降緩慢增長現象進行了深入探討，發現這種現象在高精度濾芯中更為顯著，表明即使聚結后的液體開始排出濾芯也并不能代表其內部飽和度及液體分布達到穩定。飽和度將比壓降更快地達到穩定，而壓降可能在濾芯使用周期內始終處于緩慢增長狀態。

濾芯內液體含量通常采用飽和度進行表征，因此，如果能建立操作條件、濾材結構及液體物性等參數與飽和度之間的關系，將有助于進一步闡明聚結過濾機理，同時為濾芯結構設計及性能優化提供指導。然而，目前為止僅有四種模型可用于親油型濾芯飽和預測[11-14]，如表1 所示。Liew 等[11]提供了一個相對簡單的模型，該模型需根據穩態壓降測量值進行計算，其所用實驗濾材厚度及纖維直徑較大，這與目前工業用聚結材料有明顯差異。Raynor 等[12]模型是基于0.05 m/s和0.25 m/s兩種氣速下，玻璃纖維濾芯對雙（2-乙基己基）癸二酸酯和十六烷液滴的捕獲結果而建立。然而，該模型僅適用于與其實驗具有相似結構參數的濾芯，而這些濾芯在現代工業過濾系統中并不常用。Mead-Hunter 等[13]使用兩種油劑測定了多層親油型玻璃纖維濾芯和不銹鋼纖維濾芯的壓降及飽和度，并將濾芯視為整體毛細管系統，由此根據修正Washburn 方程[15-16]和毛細管半徑與濾材物性參數之間關系[17]，給出了濾材內部液體毛細上升高度計算方法，而后利用幾何關系即可對飽和度進行預測。然而，此模型是基于1～3 層濾材的實驗結果而建立的，當濾材層數增多或整體濾材飽和度分布發生變化時，預測結果可能會出現較大偏差[18]。即便如此，多項研究均表明在靜止狀態和動態下，毛細管理論可用于描述纖維濾材的潤濕特性[16-20]。最近，Kolb等[14]提出了一種十分簡潔的模型，飽和度是過濾氣速的函數。但其中特征過濾氣速只能通過實驗來確定，且當濾材結構參數不同于其實驗濾芯時，特征過濾氣速的選取問題尚需深入探究。

表1 現有聚結濾芯飽和度模型及所適用的濾材參數Table 1 Saturation models and the applicable filter material parameters

由表1 中所列玻璃纖維濾材參數可發現，目前對于在天然氣凈化處理等實際工業過程中廣泛使用的濾材缺乏研究，此類濾材的厚度通常小于1 mm且纖維直徑在1～4 μm范圍。因此，本文首先通過實驗測定上述濾材壓降及飽和度情況，并將實驗結果與現有飽和度模型預測結果相對比。根據液體在濾芯內分布情況將飽和度進行劃分，提出新的飽和度計算方法。在此基礎上，以“跳躍-通道”模型和毛細理論為基礎建立新的飽和度預測模型。

1 實驗材料和方法

采用親油型玻璃纖維濾材作為實驗材料，濾材參數列于表2，其微觀結構如圖1所示。濾材厚度由數字千分尺測得。通過電子分析天平（AL204-IC，Mettler Toledo）可測得單位面積濾材的質量，進一步結合厚度值可獲得濾材填充密度。纖維直徑由Davies 公式[21]計算得到。濾材與實驗液體接觸角采用光學接觸角儀（Attension，Biolinscientific）進行測定。實驗濾芯由單層或多層濾材組合而成，每層濾材為直徑150 mm 的圓盤形結構。每種濾芯以其組成濾材及層數命名，例如A4 表示由4 層A 型濾材所組成的濾芯。實驗以國際通用的癸二酸二辛酯（DEHS）為氣溶膠發生液體，室溫下其密度為912 kg/m3，表面張力為0.03 N/m, 動力黏度為0.023 Pa·s。

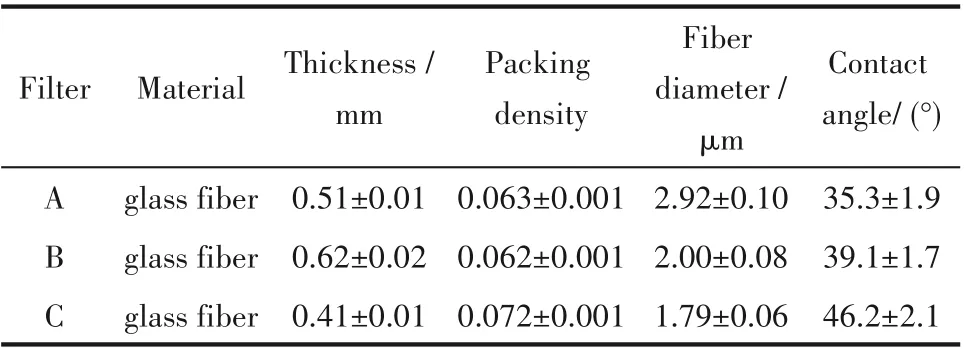
表2 實驗濾材參數Table 2 Properties of experimental filter materials

圖1 濾材B微觀結構Fig.1 SEM images of filter material B

圖2 為實驗裝置測試流程。氣溶膠發生器（ATM 240，TOPAS）產生的氣溶膠與通過高效空氣過濾器的潔凈空氣混合后，沿水平方向流經濾芯，細小液滴被纖維濾材所捕獲并以液體形式排出濾芯，過濾后的氣體最終由真空泵抽出。實驗過程中，濾芯壓降由壓差傳感器（EJX-110A，Yokogawa）實時測量。掃描電遷移率粒徑譜儀（SMPS 3936,TSI）用于測量濾芯上、下游氣溶膠濃度及粒徑分布信息。所有實驗均控制為相同的流量，使得過濾速度均為0.12 m/s。通過調整氣溶膠發生器參數，在整個實驗過程中保持液體載荷量為50 mg/(m2·s)。當壓降及排液均穩定后，表明濾芯到達穩定狀態。實驗結束后，立刻將每一層濾材進行分離并稱重，由實驗前后質量變化情況即可得到各層濾材飽和度。

2 實驗結果與討論

圖2 實驗裝置流程圖Fig.2 Schematic of experimental apparatus

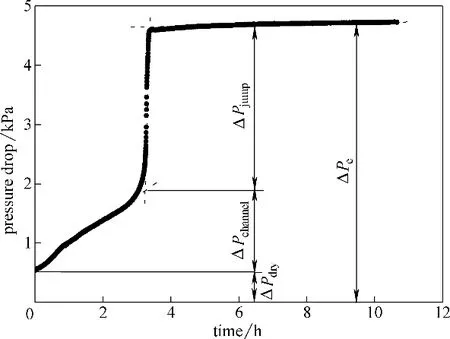
圖3 濾芯A4過程壓降曲線Fig.3 Pressure drop profile of filter A4

圖3 以濾芯A4 過濾過程壓降變化曲線為例說明壓降組成情況。根據“跳躍-通道”模型，穩態階段濾芯總壓降（ΔPe）由潔凈壓降（ΔPdry）、通道壓降（ΔPchannel）和跳躍壓降（ΔPjump）組成[3]，各壓降劃分依據及其形成機理已在前期研究中予以充分闡述[3-4]，本文不再贅述，由此本實驗中所有濾芯各壓降組成如圖4 所示。顯然對于相同濾芯而言，隨著層數的增加，潔凈壓降呈線性增長，同時更多液體進入濾芯內部對氣流造成阻力，導致通道壓降升高。然而，由于跳躍壓降僅與孔徑、纖維直徑和潤濕性等濾材屬性以及液體表面張力相關，而與過濾速度和液體載荷量等操作條件無關，因此，對于相同濾芯而言，跳躍壓降基本保持一致，不受濾材層數的影響。

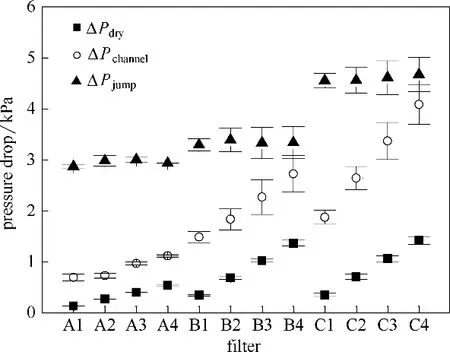
圖4 各濾芯壓降組成情況Fig.4 Pressure drop of filters with different layers

圖5為各濾芯穩態階段總飽和度及各層濾材飽和度。由圖5(a)可知，濾芯僅含單層濾材時，總飽和度最大。隨著層數的增加，總飽和度逐漸降低且逐漸趨于平緩，其原因可通過分析各濾芯內各層飽和度情況得知，如圖5(b)所示，各濾芯各層飽和度隨層數變化情況相同，且當濾材層數大于1時，液體在親油型濾芯排氣側表面會形成一層連續分布的液膜[3]，此液膜的存在將導致最后一層濾材飽和度顯著上升。另外，由于多數液滴將被首層濾材所捕獲[12,22]，從而導致其通道飽和度略高于后續各層。因此，對于單層濾材而言，液體既在其內部形成液體通道又在排氣側表面形成液膜，使得總飽和度與多層濾材相比較高。當層數增多時，同類型濾芯內平均通道飽和基本相同，而由液膜造成的飽和度在總飽和度中所占比例降低，故隨著層數的增加濾芯總飽和度逐漸趨于一致。

將表1中各種模型對本文所用濾芯飽和度進行預測，其中Liew等[11]模型和Mead-Hunter等[13]模型都需要穩態總壓降作為輸入參數，此總壓降可由圖4中各部分壓降之和得到。由于不同層數濾芯預測飽和度與實驗值對比情況基本一致，因此僅以4 層濾材所組成的濾芯為例進行說明，如圖6 所示。所有計算參數和濾材參數列于表3。需要注意的是，根據Liew 等[11]的工作，式(2)中的接觸角是靜態接觸角。采用Mead-Hunter 等[13]模型進行計算時，未采用修正系數cf（將此值設為1），因為此修正系數是由其實驗濾材參數擬合得到的，并不適用于本研究。另外，本實驗的特征速度可根據Kolb 等[10]不同載荷量下的實驗結果得到。由圖6 可知，Liew等[11]模型與Raynor 等[12]模型預測值高于實驗值，與實驗值平均相對偏差分別為50%和293%，這是由于本文實驗濾材參數與其所使用濾材存在明顯差異而造成的。另一方面，Mead-Hunter 等[13]模型和Kolb 等[14]模型預測飽和度則低于實測飽和度，與實驗值平均相對偏差分別為68%和64%。這兩種模型適用于濾芯內部潤濕區域和非潤濕區域之間有明顯界限的情況。然而，本實驗濾芯內部并非如此，如圖7 所示，其中亮色位置為液體潤濕區域，暗色位置為非潤濕區域。可見，雖然實驗所用三種濾材具有不同的結構參數，但內部潤濕情況幾乎沒有差別，這表明在實驗濾材結構參數范圍內，不同區域之間界限模糊是一種相對普遍的現象，由此使得上述兩種模型的預測結果有所偏差。此外，由于特征過濾速度僅依賴于載荷量而未考慮濾材結構參數，導致不同濾芯的預測飽和度相同。

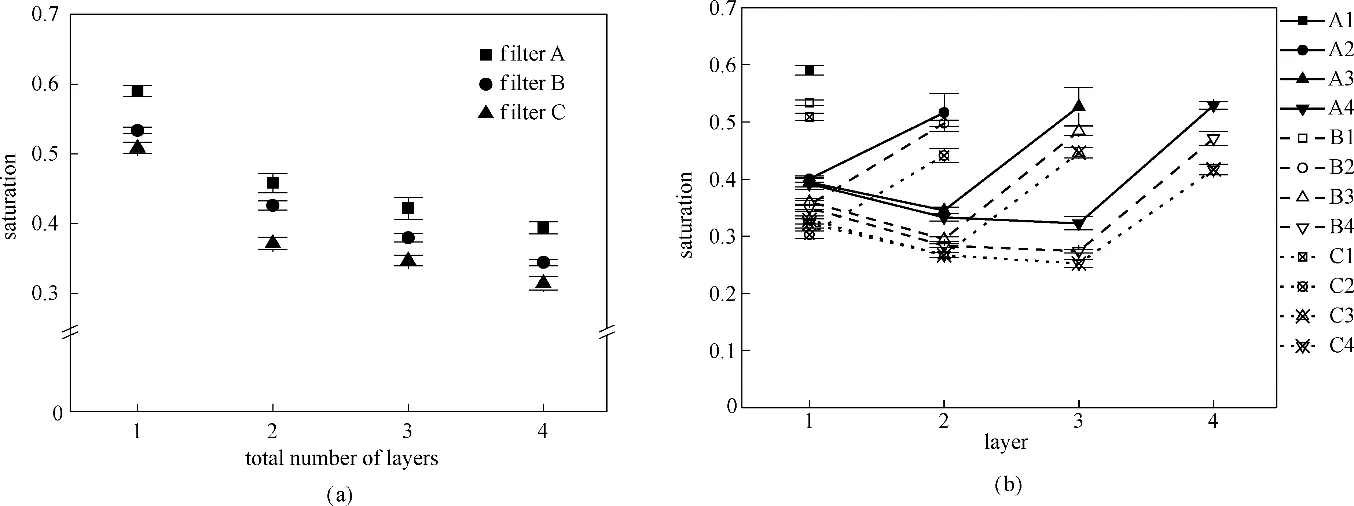
圖5 不同層濾芯總飽和度及其內部各層濾材飽和度Fig.5 Total saturation and saturation profiles of filters with different layers

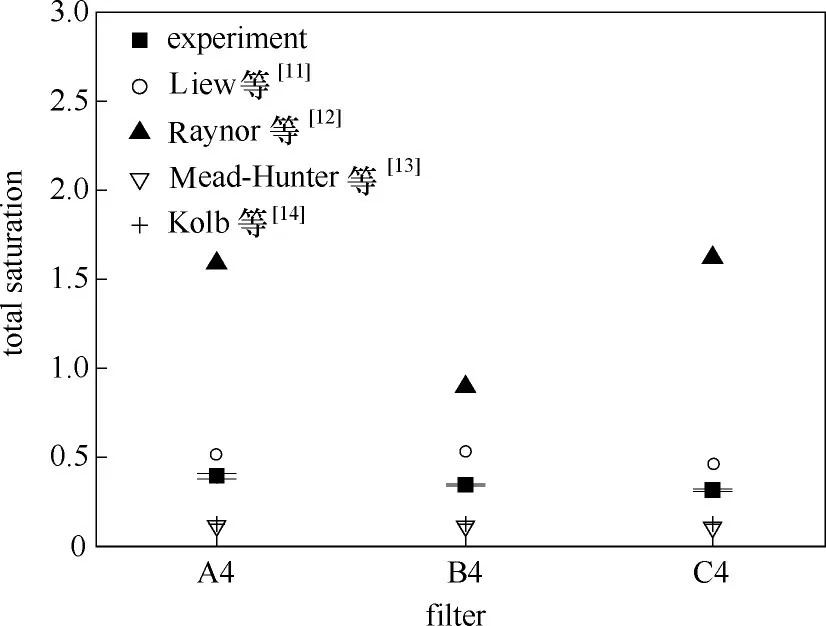
圖6 現有飽和度模型對濾芯A4、B4和C4預測值與實驗結果對比Fig.6 Comparison of predicted saturation with experimental results of filters A4,B4 and C4

圖7 濾芯A4、B4和C4內第三層濾材液體分布情況Fig.7 Liquid distribution in layer 3 of filters A4,B4 and C4 at steady state

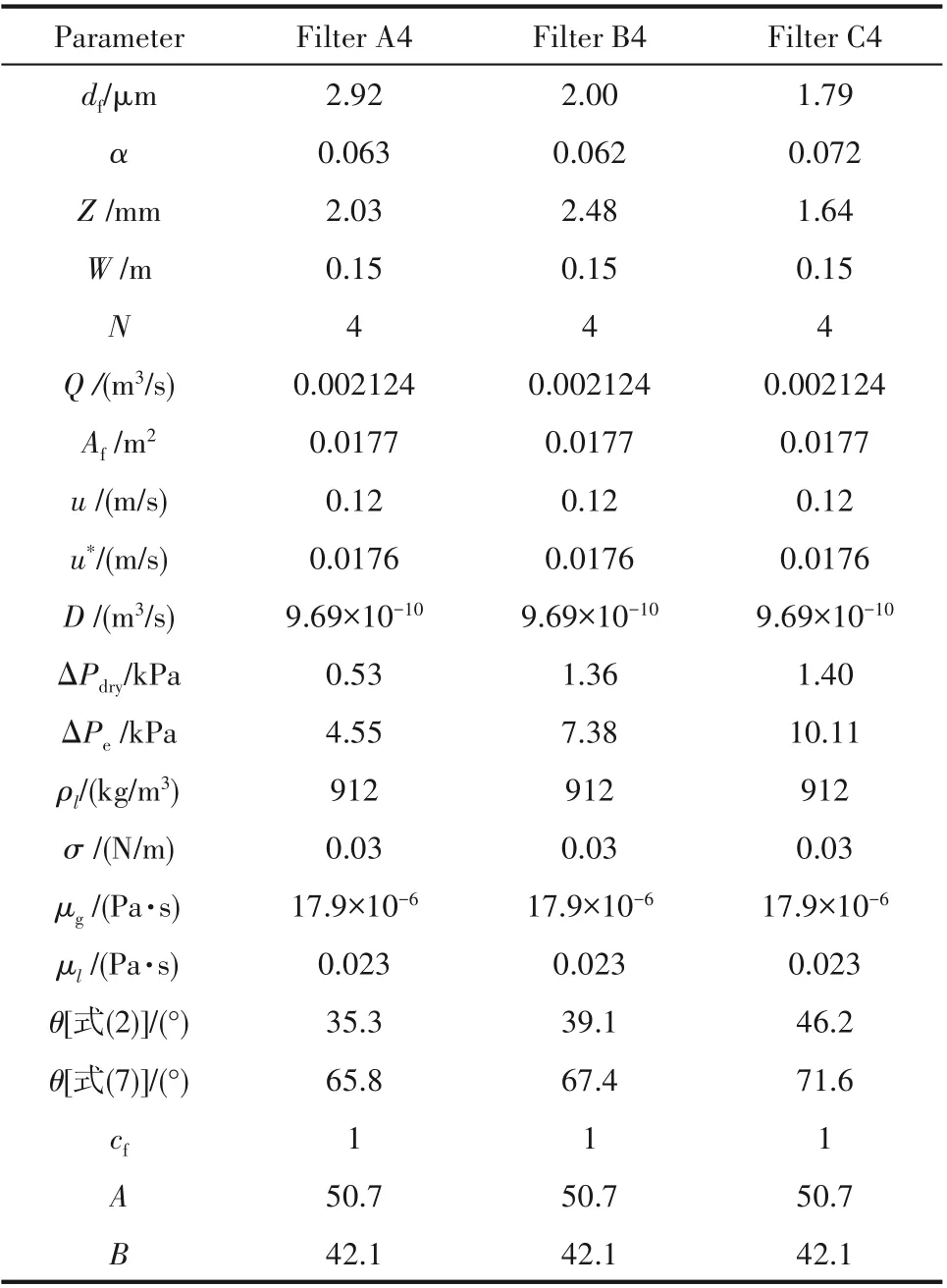
表3 濾芯A4、B4和C4飽和度預測所用參數Table 3 All parameters used to predict the saturation of filters A4，B4 and C4

由圖6 結果可知，目前存在的計算模型無法用于本文中實驗濾芯飽和度預測。顯然如果能知道每一層的飽和度，就很容易得到濾芯總飽和度。由于液體在各層濾材內運移時將形成液體通道，那么可將此產生的飽和度定義為通道飽和度（Schannel）。對于多層濾材而言，除首層和末層之外的中間濾材的飽和度僅由液體通道產生。因此，濾芯的總飽和度可以表示為：

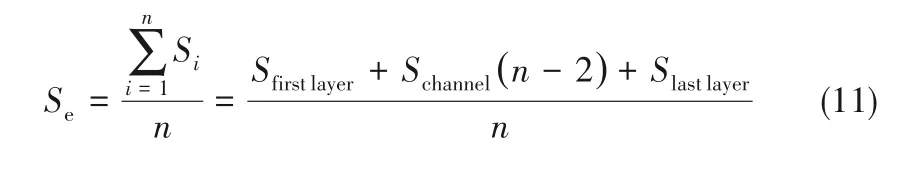
根據Kolb 等[8]的研究結果，親油型濾芯首層濾材對于液滴過濾過程與后續各層相比有所差異，因此若將首層濾材作為單獨計算區域，可得到更為準確的結果。但是，由于現階段首層濾材飽和度與后續濾材之間的液體運移關系尚未明確，若將其單獨進行計算會導致飽和度模型較為復雜。在本文中濾芯被視為一個整體毛細管系統，故各層濾材內的液體通道可統一分析。此外，從圖4 的結果可以看出，對于所有類型的濾芯，首層濾材飽和度與后續通道飽和度的差值小于5%，因此在本研究中認為首層濾材與后續濾材內飽和度近似一致。而對于最后一層濾材，根據其內部液體分布情況可以細分為兩部分：一部分為濾材內部的液體通道區域，其通道特性與前面濾材一致；另一部分為的液膜區域，液膜在濾材排氣側表面連續均勻分布，可定義此區域飽和度為液膜飽和度（Sfilm），并且Sfilm≈1。那么，總飽和度可以描述為：

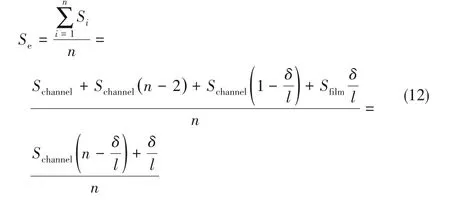
式中，δ 為液膜厚度，l 為單層濾材厚度。可見，預測總飽和度的關鍵在于如何獲得通道飽和度以及液膜厚度與單層濾材厚度比例關系。直接獲取準確的液膜厚度難度較大，因為這需在實驗過程中氣體流動狀態下實時測量方可得到。一旦氣體停止流動，液體將在濾材內重新分布，對此目前國內外學者尚無有效解決方法。然而，根據各層濾材飽和度可通過理論推導方式對液膜厚度占單層濾材厚度比值進行計算：

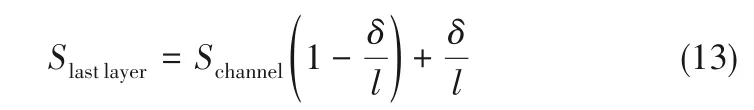
液膜厚度與單層濾材厚度比例關系則可表示為：

根據圖5(b)所示每種濾芯的最后兩層的飽和度，計算得到液膜厚度在最后一層濾材內所占比例為18%～30%，相應的液膜厚度為90～180 μm。所得比例范圍和液膜厚度與Kolb 等[8]研究結果基本一致。由此，在新模型中采用該比例范圍平均值（24%）進行總飽和度預測。另一方面，由于Mead-Hunter 等[13]模型建立基礎是將濾芯視為一個平行毛細管系統，這與本研究前提假設相同，因此可在此模型基礎上計算通道飽和度。然而，根據“跳躍-通道”模型，液膜和通道是在兩種不同作用機制下形成的，從而導致了跳躍壓降和通道飽和之間的獨立性。在這種情況下，式(8)中的壓降應該是通道壓降而非總壓降。由于實驗濾芯中液體潤濕情況與Mead-Hunter等[13]研究有較大不同，需對理論毛細管半徑進行修正并將其定義為特征毛細管半徑。綜上所述，通道飽和度可表示為：

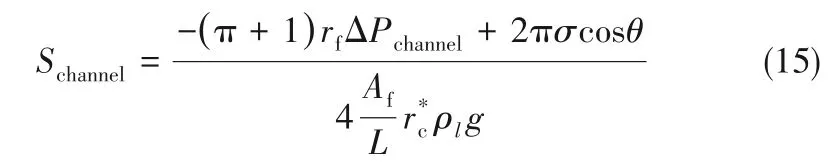
式中，Af為過濾介質面積，L 為濾材的特征長度，正交于氣體流動方向和重力方向，θ 為動態接觸角，此參數與靜態接觸角不同，無法通過實驗確定，故采用式(16)[4,12]進行計算：

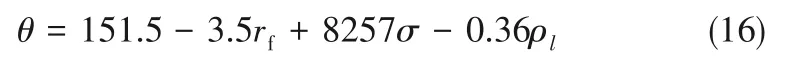
由式(16)計算得到實驗濾材的毛細管半徑為86～118 μm，動態接觸角為65°～68°。進一步，將式(15)代入式(12)，可得總飽和度為：

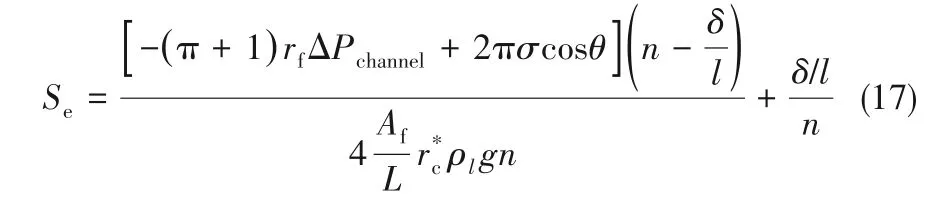
特征毛細管半徑和液膜厚度占單層濾材厚度比值對預測飽和度的影響情況，如圖8 所示。特征毛細管半徑45、50 和55 μm，濾芯的平均相對偏差分別為7.3%、2.9%和7.7%。當取值為50 μm 時預測值與實驗結果較為吻合，因此將其作為此類濾芯特征毛細管半徑。由圖7 可知，實驗濾芯內部潤濕區域和非潤濕區域之間沒有明顯的界限，表明液體在濾材內部存在橋連現象，這是導致不同結構濾材具有相同特征毛細管半徑的原因。同時根據圖8(a)結果可得到，特征毛細管半徑在45～55 μm范圍內變化時，對于結果的影響程度為：±1.43%/μm（平均相對偏差/微米）。圖8(b)則給出了液膜厚度占單層濾材厚度比值對飽和度的影響情況。當該比值為18%、24%和30%時，各濾芯的平均相對偏差分別為6.1%、2.9%和3.9%，比值在18%～30%范圍內變化時，對于結果的影響程度為±0.77%/%（平均相對偏差/百分比）。可見，預測飽和度對于特征毛細管半徑和液膜厚度占單層濾材厚度比值的變化并不敏感。換而言之，在新模型中由于上述兩計算參數的選取而引入的偏差不會對最終預測結果造成明顯的影響。

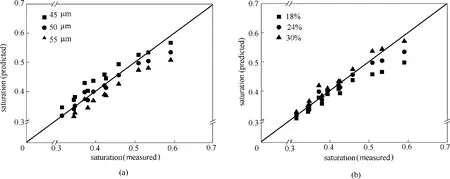
圖8 預測飽和度在不同特征毛細管半徑及液膜厚度比值條件下對比情況Fig.8 Comparison of predicted saturation with different characteristic capillary radii and fractions

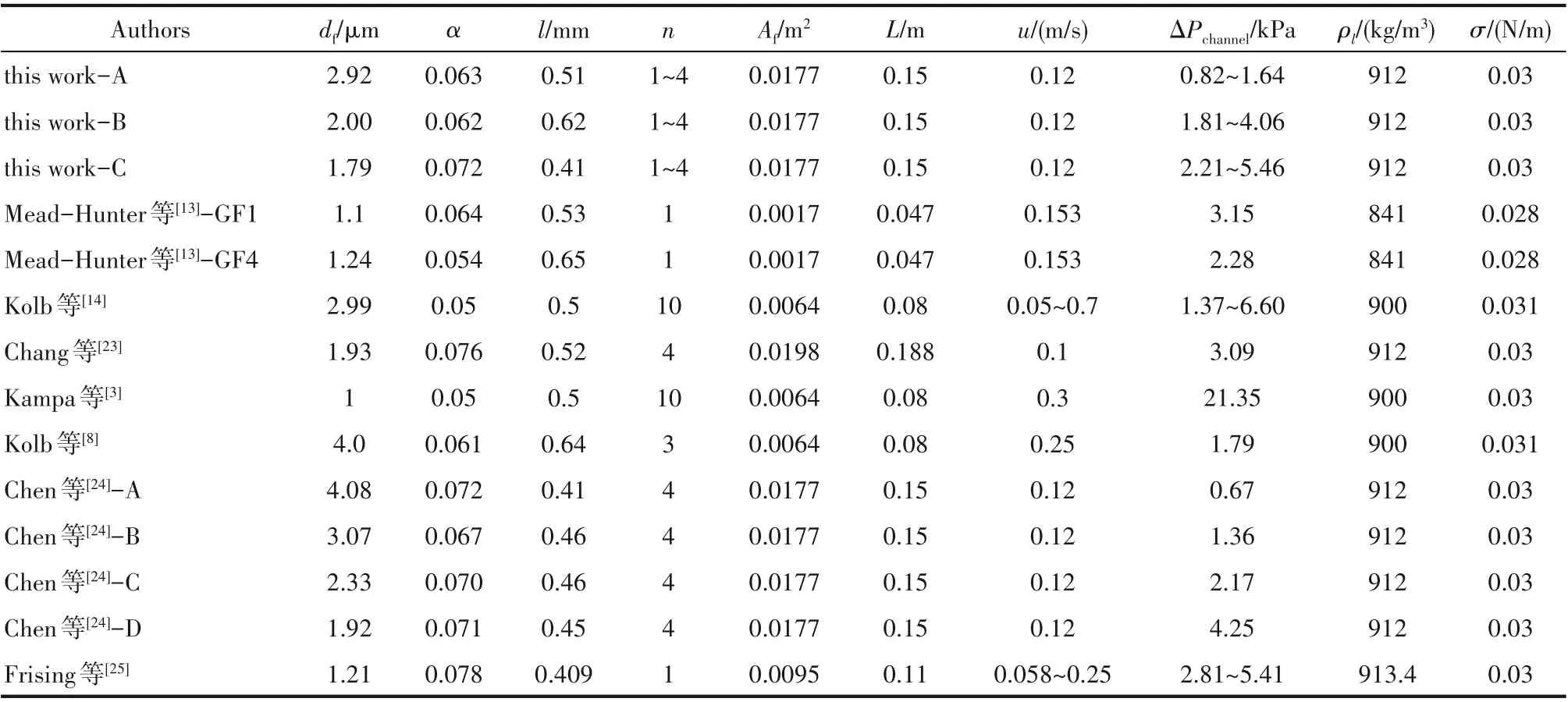
表4 新建飽和度模型預測所用計算參數Table 4 All parameters used for predicting saturation

將建立的新飽和度模型對親油型濾芯飽和度進行預測，各計算參數列于表4，其中濾材和實驗液體物性參數可從各文獻中直接獲得，動態接觸角可由式(16)得到。部分文獻中直接給出了通道壓降，而對于未直接給出的則使用Plot數字轉換器軟件從原文過程壓降曲線進行提取。在提取數據前，首先利用轉換器對原文中壓降曲線的x 軸和y 軸坐標進行校準，然后即可準確獲得壓降曲線中任意一點數值。需要注意的是，Mead-Hunter等[13]的工作中只給出了總壓降，由于其實驗濾材與本文較為接近，基于本文濾芯實驗結果將30%的總壓降作為通道壓降參與計算。Kolb 等[14]的工作中未給出液體密度，此處根據其課題組Kampa等[3-4]前期工作而設定。

圖9給出了新飽和度模型預測值與目前已有實驗結果對比情況。大多數實驗結果飽和度均大于0.2，此時預測值與實驗值吻合度較好，最大相對偏差≤20%。然而，Kolb 等[14]實驗濾芯的飽和度小于0.2 時，預測結果并不理想，這主要是由于其實驗濾材內液體通道相互獨立，潤濕區域和非潤濕區域之間的邊界非常明顯，與本實驗中的濾芯潤濕情況完全不同。其次，Kolb 等[14]工作中并未直接給出液體密度，由此可能會導致預測值出現一些偏差。此外，新模型中未對首層濾材單獨計算，若首層濾材飽和度明顯高于中間層濾材時，將導致預測結果出現偏差，這種偏差在低飽和度時將更為明顯。一般而言，隨著飽和度的降低，濾芯潤濕和非潤濕區域界限將逐漸明顯，此時模型中毛細管半徑無需修正。因此，對于低飽和度情況可仍然采用式(17)進行計算，但其中毛細管半徑需由式(9)得到。圖9 中也給出了根據此方法對Kolb等[14]濾芯重新計算的結果，預測值與實驗結果吻合程度顯著提高，最大相對偏差≤30%。而由表4 中所列參數可知，過濾速度主要在0.05～0.3 m/s區間，屬于實際工業用濾芯典型氣速范圍，這意味著新建模型可在較寬的操作條件下，有效預測由微米級玻璃纖維濾材所組成的濾芯飽和度。

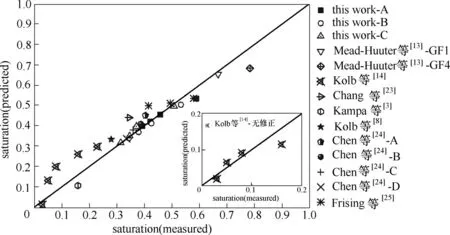
圖9 新模型飽和度預測值與實驗結果對比情況Fig.9 Predicted and measured total saturation

3 結 論

本文研究了由厚度較薄且纖維直徑為1～4 μm濾材成的多組層親油型濾芯壓降及飽和度情況，經計算可知，現有的飽和度模型無法對此類濾芯進行準確的預測。根據液體在濾芯內分布情況可將飽和度劃分為通道區域及液膜區域。為預測通道飽和度，可采用Mead-Hunter 等[13]提出的毛細管模型進行計算，但由于本研究中的濾芯非飽和區域和飽和區域沒有明顯的界限，需結合“跳躍-通道”模型和實驗結果對其進行修正。新的飽和度模型對已有文獻濾芯計算結果表明，當飽和度大于0.2 時，預測值與實驗結果相對偏差≤20%，在可接受范圍之內。當飽和度小于0.2 時，隨著飽和度的降低，濾芯潤濕區域和非潤濕區域之間界限逐漸明顯，此時模型中毛細管半徑無需修正，在此條件下預測值與實驗結果相對偏差≤30%。然而，所建立的模型仍受限于需采用通道壓降測量值作為輸入參數。因此，在后續工作中需構建通道壓降與濾材結構和液體物性等參數之間的關系，從而進一步提高預測模型適用性。

符 號 說 明

A——濾材特定常數

Af——濾材面積，m2

B——濾材特定常數

Bo——Bond數

Ca,Can——毛細管數

cf——毛細管半徑修正因子

D——排液率，m3/s

Dr——無量綱排液率

df——纖維直徑，μm

g——重力加速度，m/s2

L——濾材的特征長度，m

l——單層濾材厚度，mm

n——濾材層數

ΔPc——理論毛細管頂端與底端壓降，kPa

ΔPchannel——通道壓降，kPa

ΔPdry——潔凈濾芯壓降，kPa

ΔPe——穩態壓降，kPa

ΔPjump——跳躍壓降，kPa

Q——氣體流量，m3/s

rc——毛細管半徑，μm

rf——纖維半徑，μm

Schannel——通道飽和度

Se——平衡狀態下總飽和度

Sfilm——液膜飽和度

Si——第i層濾材飽和度

u——過濾氣速，m/s

u*——特征過濾氣速，m/s

W——濾芯寬度，m

x∞——穩態時毛細管上升高度，m

Z——濾芯厚度，mm

α——填充密度

δ——液膜厚度，μm

θ——液體與濾材靜態/動態接觸角，(°)

μg——氣體黏度，Pa·s

μl——液體黏度，Pa·s

ρl——液體密度，kg/m3

σ——液體表面張力，N/m