電磁扭桿離合器工作溝槽接觸應力分析

石松，盧曦

（200093 上海市 上海理工大學 機械工程學院）

0 引言

電磁扭桿離合器具有傳遞扭矩、減振和有效避免傳動系過載的作用，彈性扭桿組件上的鋼球與離合盤上的工作溝槽結合后開始傳遞扭矩，但在彈性扭桿組件鋼球與離合盤工作溝槽結合-分離的過程中，仍然存在力矩傳遞效率不佳的情況[1-3]，因此，離合盤工作溝槽為電磁扭桿離合器傳遞扭矩的關鍵所在。

本文以某新型電磁扭桿離合器工作溝槽為研究對象，以彈性扭桿組件上鋼球與離合盤溝槽的壓力角和接觸應力之間的關系為研究目標[4-6]，首先通過電磁扭桿離合器的運動機理進行力矩傳遞分析，確定彈性扭桿組件上的鋼球與離合盤工作溝槽為主要承載部位，進而提出工作溝槽與鋼球之間的接觸應力與壓力角變化關系，最終通過確定壓力角達到提高電磁扭桿離合器的力矩傳遞效率和保障強度的目的[7-9]。

1 材料與方法

某新型電磁扭桿離合器主要由2 個離合盤、1 個中間盤以及4 根彈性扭桿組件構成，彈性扭桿組件由3 個鋼球、1 根彈性扭桿以及1 個永磁體塊組成。外部轉矩經過主軸通過彈性扭桿組件帶動中間盤轉動，并將扭矩傳遞給離合盤轉動，從而實現離合器的驅動和制動過程。驅動與制動過程示意圖如圖1 所示。

由力矩傳遞路徑可以得出結合后彈性扭桿組件為傳遞過程中的樞紐，而彈性扭桿組件上的鋼球與離合盤工作溝槽為主要受力承載點，即接觸應力較大位置。電磁扭桿離合器在運動過程中鋼球與溝槽結合。一方面，為了保障離合盤驅動，接觸應力不能過大造成強度不能得到保障，鋼球在溝槽中的壓力角一般設計為小于20°；另一方面，同時要保障分離過程中彈性扭桿組件能從工作溝槽中及時分離，避免發生自鎖現象。因此，下文將研究鋼球在溝槽中的接觸應力與壓力角的匹配關系。鋼球在溝槽中空間受力簡圖如圖2 所示。

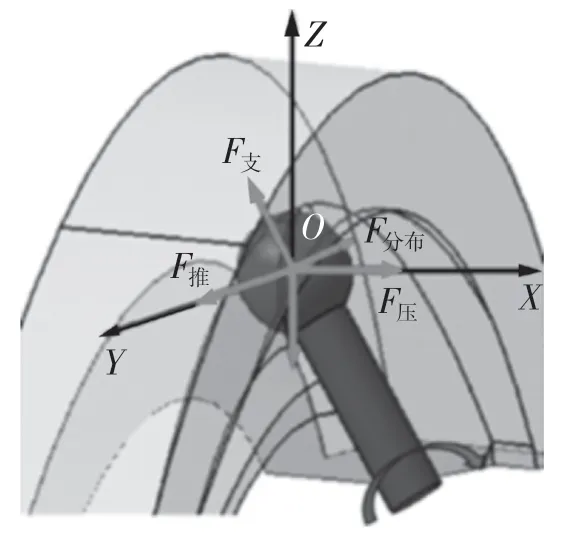
圖2 鋼球在溝槽中受力Fig.2 Stress of steel ball in groove

鋼球在溝槽中的受力主要為推力，其他如重力、分布力、摩擦力以及支持力可忽略不計，具體的鋼球在溝槽中的受力情況分析二維視圖如圖3 所示。

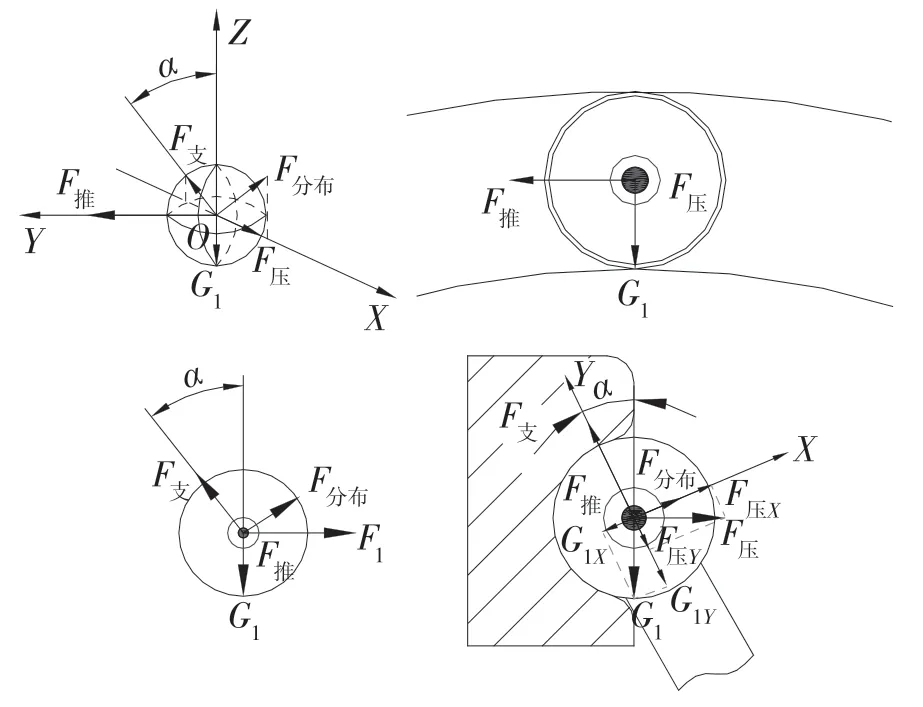
圖3 鋼球在結構中受力分析Fig.3 Stress analysis of steel ball in structure

電磁扭桿離合器的工作機理可以總結為：未接合之前，彈性扭桿組件處于主轉盤的桿槽內并隨著主轉盤轉動而轉動，線圈通電后產生電磁力吸附磁體塊，在引力的作用下，扭桿組件將以2號球為轉動支點轉動，扭桿組件上1 號球進入導向槽內，最終滾動進入離合盤上的凹槽實現接合，接合狀態如圖4 所示。該電磁扭桿離合器最大傳遞轉矩可達300 N·m，最高轉速可達10 000 r/min。因此可確定，鋼球與溝槽承載部位接觸應力較大，結構模型及尺寸二維視圖如圖4、圖5 所示。

圖4 彈性扭桿擺動剖視圖Fig.4 Swing section of elastic torsion bar

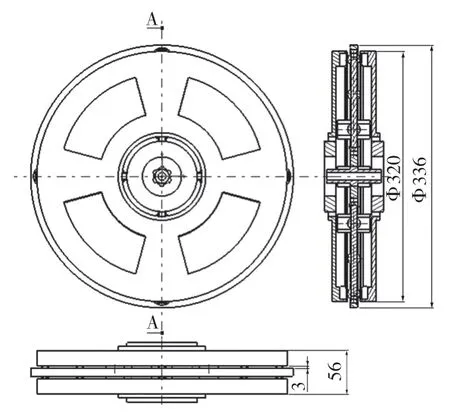
圖5 電磁扭桿離合器二維視圖Fig.5 Two-dimensional view of electromagnetic torsion bar clutch

如圖6 所示，某新型電磁扭桿離合器工作溝槽接觸應力分析步驟如下：

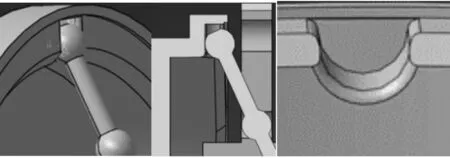
圖6 鋼球與工作溝槽接合Fig.6 Joint of steel ball and working groove

（1）通過分析電磁扭桿離合器運動機理和力矩傳遞方式，確定受力承載部位為離合盤工作溝槽，通過理論推導計算得到鋼球與工作溝槽之間的接觸應力與壓力角之間的關系，并以此關系設計出最佳壓力角滿足力矩傳動和強度要求。

（2）建立彈性扭桿組件上鋼球與離合盤結合狀態時的仿真計算模型，利用有限元軟件定義連接關系、接觸關系，在所設計的壓力角下進行有限元仿真分析溝槽的接觸應力大小，驗證在所設計的壓力角下鋼球與溝槽之間的接觸應力大小。

（3）對比仿真計算與理論計算接觸應力結果，分析出現理論計算與仿真計算出現差異的原因，在此基礎上進行接觸應力校核，并得出鋼球與工作溝槽之間壓力角度數可以滿足力矩傳遞的要求以及應力要求。

2 接觸應力的理論計算分析

彈性扭桿組件鋼球與離合盤工作結合后，鋼球與工作溝槽的曲率不一樣會導致鋼球位于溝槽底部偏上某一點，由于鋼球與溝槽為受力承載部位，則接觸點部位接觸應力較其他地方大，由于鋼球強度較大，這里不選取鋼球作為接觸應力計算對象，而選取工作溝槽為研究對象。電磁扭桿離合器布置有4 根彈性扭桿組件，這里為了計算方便，選取一根彈性扭桿組件為例，離合盤上的工作溝槽傳力截面規定為鋼球與工作溝槽結合狀態時的承載截面，截面A-A 即為承載截面。傳力截面為橢圓形，截面形狀如圖7 所示。其中，L為工作溝槽寬度，H 為深度，角度α為壓力角。

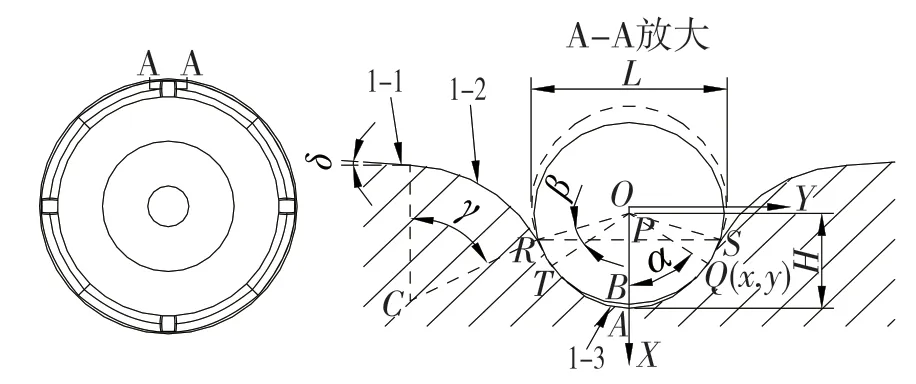
圖7 工作溝槽示意圖Fig.7 Schematic diagram of working groove

由橢圓基本方程可得工作溝槽的橢圓形溝道一般方程可表示為

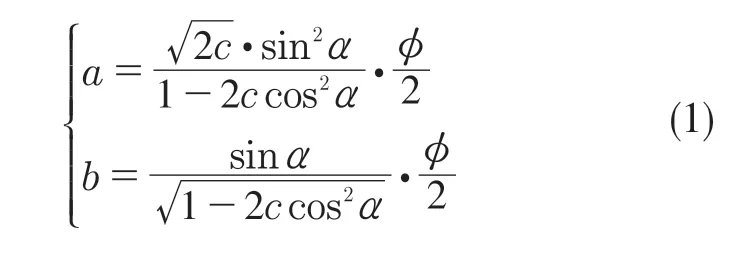
鋼球與溝道之間的接觸形式為球和圓柱的接觸面，可以通過赫茲接觸應力的理論計算方法進行計算。在計算接觸應力的過程中，首先需要把鋼球與溝槽接觸面的正壓力計算出來，而正壓力由傳遞扭矩得到，外部轉矩經主軸傳遞給主轉盤，通過彈性扭桿組件帶動離合盤轉動。該電磁離合器的工作轉矩可達300 N·m，傳遞扭矩與正壓力的關系式可表示為

式中：Q——正壓力；n——鋼球數量；D——分度圓直徑；M——傳遞扭矩。

接觸應力是指兩個接觸物體相互擠壓時在接觸區及其附近產生的應力。圓柱面與球面的接觸應力計算公式表示為

式中：Q——正壓力；a——接觸橢圓長半軸；b——接觸橢圓短半軸。

當已知接觸表面的主曲率后，就可以確定接觸橢圓率，進一步可以計算得出第1 類和第2 類完全橢圓積分，最后可求出接觸區橢圓半軸的長度。利用簡化公式方便計算如下式所示：

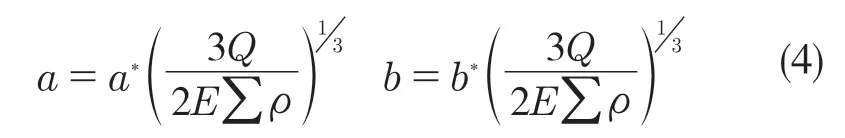
式中：a*，b*——赫茲應力系數，由計算如下幅值函數的值從而查表得到；∑ρ——主曲率和；E——材料的彈性模量。

為方便計算接觸應力，建立輔助函數。設曲面的2個方向上主曲率半徑為ρ11，ρ21，ρ12，ρ22則定義輔助函數F（ρ）。

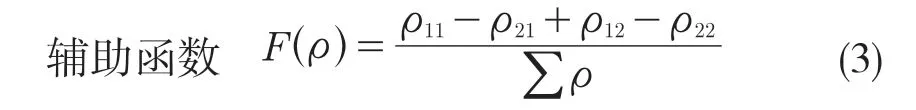
查表可以得到赫茲應力系數。

式中：Dw——鋼球直徑；D——鋼球中心圓；f——軌道曲率比；θ——壓力角。

其中，鋼球與溝槽之間的壓力角是一個關鍵的參數，其與施加的壓力的大小有關，會因為施加力的不同，導致壓力角發生變化。壓力角按照間隙和力平衡確定，在鋼球運動到正常工作位置時其壓力角為15.6°。

最終接觸應力及相關計算參數的計算結果如表1 所示。

得到接觸應力與壓力角的變化關系，最終壓力角選擇設計為15.6°。通過理論計算下的鋼球與工作溝槽之間的接觸應力大小為1 456 MPa。

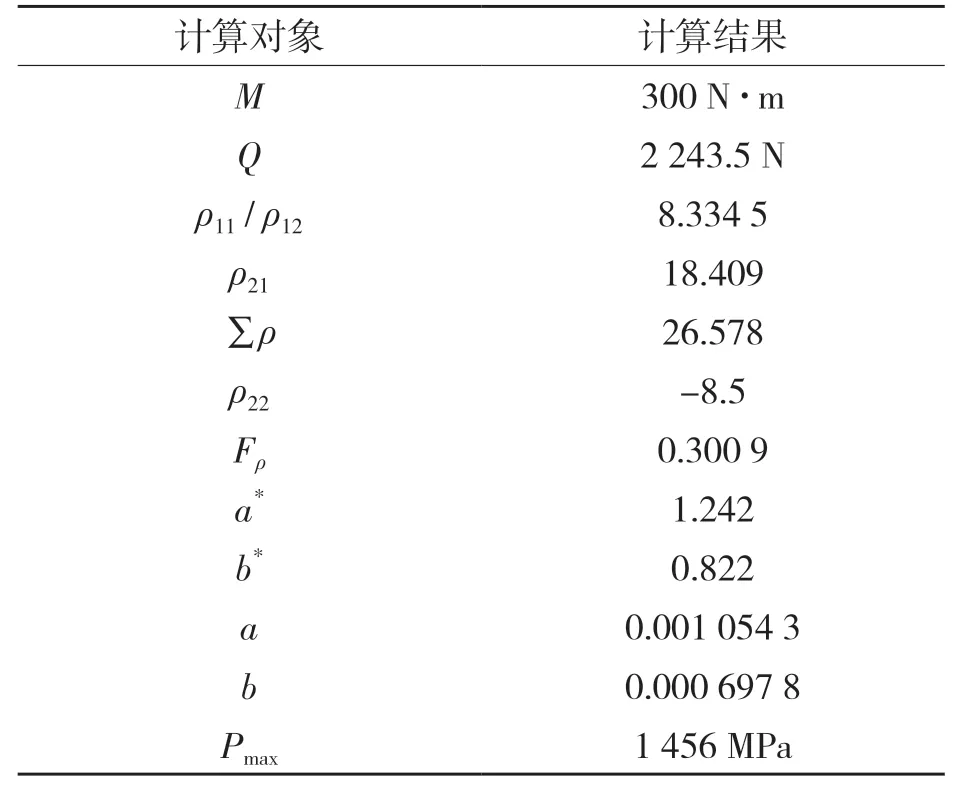
表1 理論計算結果Tab.1 Theoretical calculation results

3 有限元仿真分析

3.1 建立仿真模型

彈性扭桿采用彈簧鋼材料，其他部件材料采用45#鋼，為優質碳素結構鋼，是線性材料。具體參數如表2 所示。

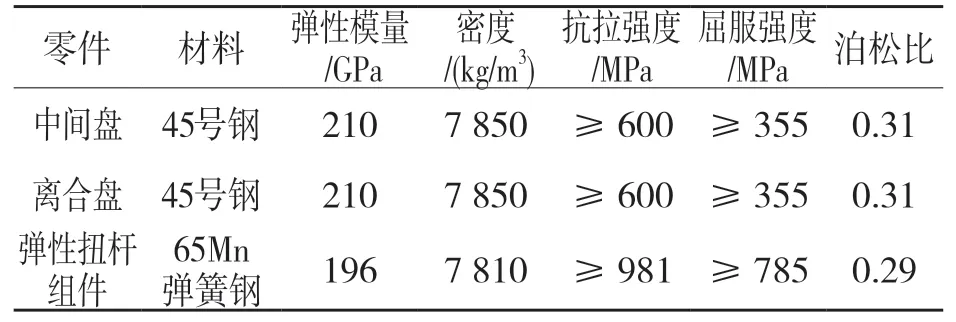
表2 各零部件的材料及特性Tab.2 Materials and characteristics of parts

裝配后的模型如圖8 所示。

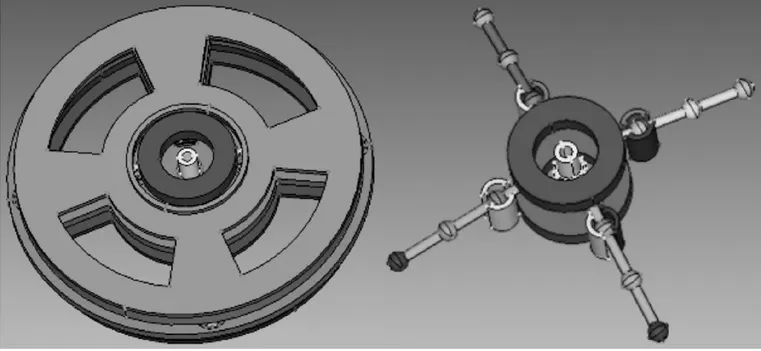
圖8 裝配模型Fig.8 Assembly model

3.2 有限元仿真分析

3.2.1 仿真過程前處理

由于離合盤工作溝槽為傳力的主要部位，因此鋼球與工作溝槽接觸部位應該細化網格。

（1）材料特性：將三維模型導入有限元軟件Workbench 中，對各個零件分別賦予相應的材料和機械特性。

（2）定義接觸關系：使用面接觸定義目標面和接觸面，接觸設置為bonded。

（3）劃分網格：接觸區域網格足夠細化，使計算結果近似準確[10-11]。先采用整體網格劃分，尺寸為2 mm，然后用局部網格細化的方法對關鍵部位進行網格細化，細化等級三級，細化后尺寸為1 mm,劃分結果總共有82 575 個節點，44 297 個單元，運用網格質量檢查功能檢查網格質量[12]，平均質量為0.845 4，符合要求。如圖9所示。

圖9 網格劃分Fig.9 Grid generation

（4）載荷及約束條件：為計算方便，將4根彈性你桿組件看做1 根彈性扭桿組件作用，因此單根轉矩為75 N·m。

3.2.2 仿真結果

由于離合盤為4 根彈性扭桿組件傳力所驅動，故可將模型簡化為1 根彈性扭桿組件驅動，通過施加扭矩可計算得到單根彈性扭桿組件上鋼球與離合盤工作溝槽的接觸應力，最終得到仿真計算結果為鋼球與工作溝槽之間的接觸應力為1 350 MPa 左右，與理論計算結果1 456 MPa 存在差異。有限元仿真計算結果如圖10 所示。理論計算結果與仿真計算結果大體一致則說明實際接觸應力遠小于最高接觸應力，完全滿足強度要求。

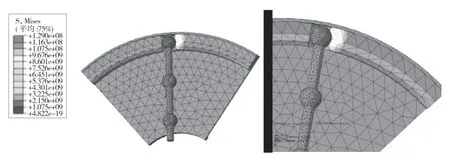
圖10 仿真計算結果Fig.10 Simulation results

3.2.3 計算結果分析

接觸應力理論計算結果為1 456 MPa，仿真計算結果為1 350 MPa，仿真計算結果較理論計算結果偏低，可能原因有：（1）有限元分析計算過程中，溝槽部位網格質量較差；（2）施加載荷即傳遞扭矩過程中有偏差。在仿真計算過程中無法消除，只能盡可能減小。理論計算結果和仿真計算結果數值相差不大，基本認為兩者結果一致，從而可驗證接觸應力計算合理。

電磁扭桿離合器工作溝槽接觸應力可以參考等速傳動萬向節的接觸應力，鋼球在溝道中的最高接觸應力為4 200 MPa，對于本例中具有2.88的安全系數，滿足強度要求，因此可以初步判斷結果鋼球與工作溝槽之間的壓力角為15.6°能滿足接觸應力要求，在扭桿組件分離過程中也可以滿足脫離溝槽的要求。

4 結論

（1）通過分析電磁扭桿離合器運動機理確定受力承載部位為離合盤工作溝槽后，得到彈性扭桿組件上鋼球與離合盤工作溝槽之間的壓力角與接觸應力的關系，通過理論推導計算，得到鋼球與工作溝槽之間的接觸應力為1 456 MPa。

（2）建立彈性扭桿組件上鋼球與離合盤結合狀態時的仿真模型，利用有限元軟件定義連接關系、接觸關系，進行有限元仿真分析計算，得到仿真計算結果為1 350 MPa。

（3）參考等速傳動萬向節的接觸應力，最高接觸應力為4 200 MPa，對于本例中具有2.88的安全系數，初步可以判斷結果鋼球與工作溝槽之間的壓力角為15.6°能滿足接觸應力要求，可以保障其力矩傳遞而不發生自鎖的要求，可為下一步動力學分析作準備。