福州地區汽車行駛工況構建與研究

劉文武

（200093 上海市 上海理工大學 機械工程學院）

0 引言

汽車行駛工況（Driving Cycle）是描述汽車行駛的速度-時間的曲線[1]。國家工信部根據該曲線來實驗測算汽車油耗，所以工信部油耗是否與實際油耗相吻合與汽車行駛工況曲線有密切關系。目前我國采用的是歐洲NEDC 汽車行駛工況[2]，但隨著汽車保有量的快速增長以及道路交通狀況的變化，NEDC 與我國實際情況產生的誤差越來越大，所以制定反映我國實際道路行駛狀況的測試工況顯得越來越重要。我國地域遼廣，各個城市的發展程度、氣候條件及交通狀況不同，各城市間的汽車行駛工況存在明顯的差異性，基于城市自身的汽車行駛數據進行城市汽車行駛工況的構建研究也越來越迫切。

陳漢[3]等利用GPS 設備采集的哈爾濱市8 個區域的行駛數據構建了乘用車的出行特征，利用主成分分析方法和聚類分析方法構建出哈爾濱市乘用車工況。劉鵬[4]等提出一種組合主成分分析和聚類分析的數據處理方法，得出西安市區城市客車瞬態行駛工況，并采用樣車進行仿真分析，進一步對XATD-HBUS 工況及ECE 工況之間的差異進行了對比驗證。姜平[5]等基于離散小波變換數據壓縮理論對行駛數據進行壓縮重構，根據特征參數構建了城市道路代表行駛工況，并建立合肥市區典型道路的11 個行駛工況評價準則。彭育輝[6]等采用優化聚類與馬爾科夫鏈的組合方法構建出城市環衛車輛行駛工況，并基于運動學參數的有效性對行駛工況進行了驗證，證明了工況構建方法的有效性和合理性。李耀華[7]等基于馬爾科夫鏈構建了西安市城市公交某路線工況，采用特征值來驗證該方法的有效性。

根據提供的數據建立一條能體現參與數據采集汽車行駛特征的工況曲線，使該曲線所體現的汽車運動特征能代表所采集數據的相應特征。

1 數據采集與預處理

1.1 數據采集

為使采集的數據更能充分地反映福州地區的交通狀況，汽車行駛工況數據采集應該有足夠廣的覆蓋面。數據采集主要在福州地區城市道路上進行，路線包括市區道路、學校、車站、商業中心及高速、機場一些交通流量比較大的地方。通過GPS+傳感器設備對車輛行駛的速度、三向加速度、經緯度以及燃油消耗率等數據進行采集。連續采集了3 周，采樣頻率為1 Hz，共采集了496 467 組數據。圖1 所示為采集的數據繪制出的車輛運動軌跡。

圖1 數據采集車輛行駛路線Fig.1 Data collection vehicle driving route

1.2 模型假設

假設：（1）汽車正常的怠速范圍在600～800；（2）實驗期間自然環境對采集設備的影響一致；（3）GPS 速度＜1 和＜0.1 包含在汽車怠速抖動范圍內；（4）數據采集中汽車的動力性能及燃油經濟性等幾個指標不發生變化；（5）不考慮汽車行駛過程中的風阻系數等因素的影響；（6）x 為汽車的前進方向，y 為轉彎方向，z 為垂直方向，如圖2 所示。

圖2 汽車運動學模型Fig.2 Kinematics model of the car

1.3 不良數據分析及處理

不良數據的存在使得數據系統丟失了大量有用信息。

（1）GPS 信號丟失造成的時間不連續。當汽車駛入高層建筑、隧道等路段或GPS 設備受到干擾影響時，可能出現丟失信號的情況。缺失值中大部分是穿越高層、短隧道的短時間斷點；小部分是停在地下車庫但采集設備仍在運行，以及穿越長隧道的長時間斷點。小于10 s 的斷點對汽車工況曲線的構造的影響不大，使用Python 中的pandas 庫遍歷所有時間數據找到數據丟失造成的時間斷點，采用均值插補方式進行插補；對10 s以上的斷點進行補全會影響運動學片段的劃分從而影響曲線構造的準確性，所以不作處理。經過處理發現斷點有4 196個，補全的數據有3 693個；

（2）汽車加、減速度異常數據。一般情況下，普通轎車最大減速度為8 m/s2，且0～100 km/s 的加速時間大于7 s，a 不在3.968 25～8.000 00 m/s2范圍內的均視為異常值，這類數據對汽車工況曲線的準確性產生重要影響。處理方法是異常值所對應的GPS 車速清空，然后使用拉格朗日插值法進行插值計算；

（3）長期停車，如停車不熄火等候人、停車熄火了但采集設備仍在運行、發動機冷啟動后怠速熱車、停車后不立即熄火等情況所采集的異常數據應該直接移除，總共刪除的長期停車異常數據有593 個；

（4）加速是指汽車加速度＞0.1 m/s2的連續過程，減速是指汽車加速度＞-0.1 m/s2的連續過程，而勻速是指汽車加速度絕對值＜0.1 非怠速的連續過程。故長時間堵車可以理解為車速范圍為0＜v＜1，且加速度范圍為-0.1＜a＜0.1 的行駛過程，斷斷續續低速行駛則可理解為1＜v＜10，且a≤-0.1＜∪a≥0.1 的行駛過程。長時間堵車和斷斷續續低速行駛這類數據的存在會影響到運動片段的劃分，應作歸零化處理。刪除掉的長時間堵車和斷斷續續低速的數據有15 979 個；

（5）一般認為怠速時間超過180 s 為異常情況。在汽車非行駛時間段繼續進行數據采集，這就造成了長時間的怠速段。對超過180 s 的這部分數據進行刪除，以免造成構建的車輛行駛工況的怠速比例較高、車速較低的情況，影響車輛行駛工況構建的準確性[8]，共刪除的長期停車異常數據有15 150 個。

針對不同的不良數據，采取適合的處理方式對5 類不良數據進行篩除，經過處理以后的數量統計如表1 所示。

表1 不良數據處理統計Tab.1 Statistics of bad data processing

2 運動學片段分析

2.1 特征值的選取

運動學片段是指汽車兩個怠速之間的行駛片段，一個完整的運動學片段通常包括4 個行駛工況：怠速、加速、減速和勻速工況[9]。此外還應該滿足：每個運動學片段的時間長度應在20 s以上；每個運動學片段的運行里程應在10 m 以上；加速度在0.100 00～3.968 25 m/s2，減速度在-8.0～0.1 m/s2的范圍內。使用MATLAB 編寫的程序對篩選后的數據系統進行運動學片段的劃分，最后共計得出的片段為5 984 個。

特征值數量過少會使得不能完全囊括運動學片段的信息而造成描述不準確，最終搭建的汽車行駛工況曲線失真；數量過多則會造成信息重復冗雜而加大計算難度，浪費人力物力資源。描述運動學片段的特征值有很多，最常用的是速度和加速度，但僅這兩個參數對運動學片段進行描述會使得信息不完善，并且在劃分運動學片段時，不同片段之間的加速和加速度數量具有差異性，這樣會導致計數緯度不同，加大分析的難度，因此本文選取了平均速度、平均行駛速度等9 個特征值來描述運動學片段信息，如表2 所示。

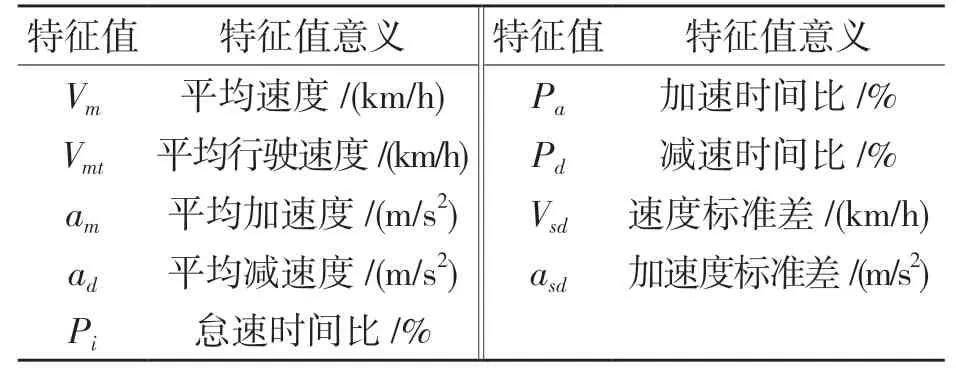
表2 特征值統計Tab.2 Eigenvalue statistics

確定好特征值的計算方法后，在MATLAB中用遍歷數據判斷法計算出5 984 個運動學片段的特征值，部分計算結果如表3 所示。

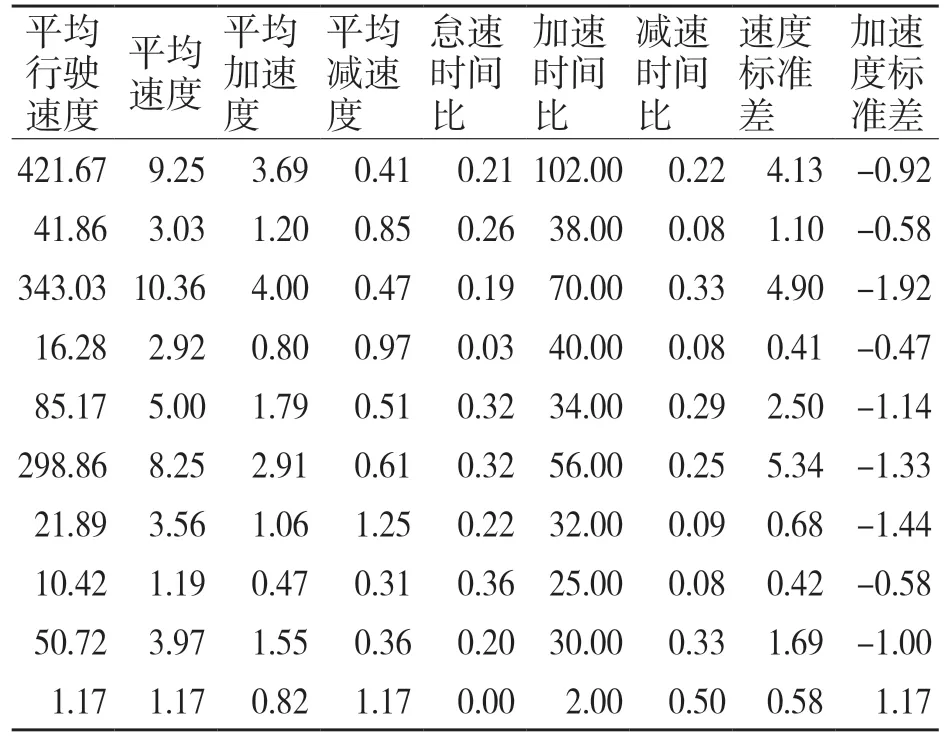
表3 特征值計算結果Tab.3 Eigenvalue calculation results

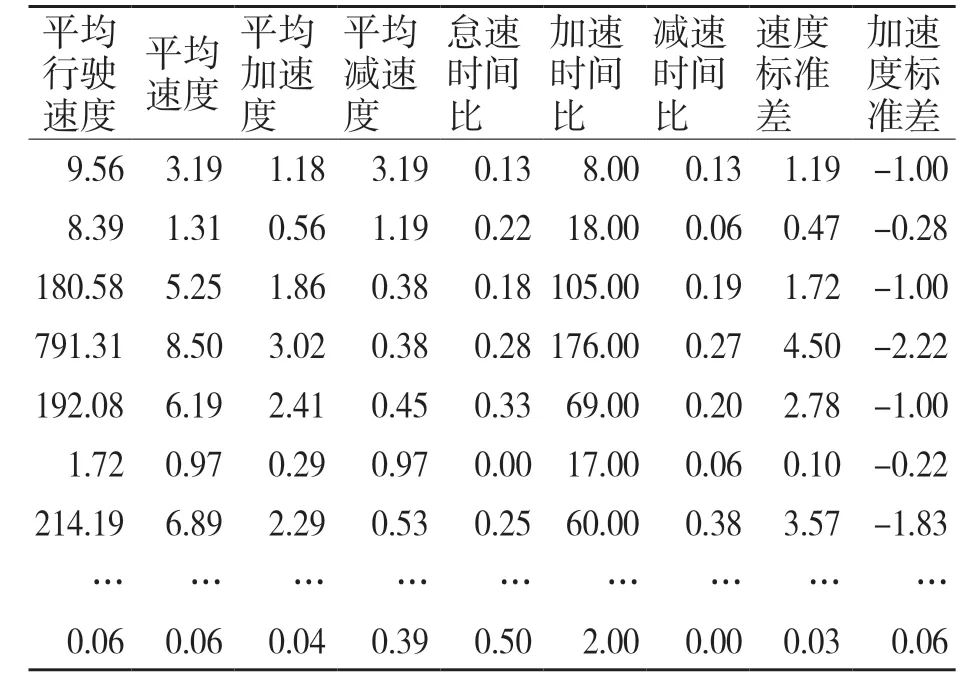
（續表）

2.2 主成分分析

為了構建全面而接近真實的汽車行駛狀況，需要對特征值進行分析，但各特征值數據重復冗余，如果完全采用高維度的運動學片段特征值進行分析，盡管能保留數據的完整信息，但由于變量存在交疊信息，會導致模型復雜、增加無效工作，并且曲線的準確性也會降低，所以在計算前需要通過主成分分析進行數據降維處理以簡化計算[10]。

處理后的運動學片段數據采用9 個特征值來描述運動學片段信息，得到特征值數據集。

相關系數絕對值越大，該主成分與這些特征參數的相關性越高，主成分代表性越強。相關系數絕對值較大表明該主成分綜合了這幾個相關系數絕對值大的特征參數，該主成分的代表性越強。其中平均速度、最大速度、平均加速度為第1 主成分的特征值信息；第2 主成分與運行時間、平均減速度、加速比例和減速比例的相關性較高；怠速比例和勻速比例的特征值信息為第3 主成分；第4 主成分代表最大加速度和最小減速度的特征值信息[11]。

短行程對應的主成分得分是由標準化的特征參數矩陣與主成分系數矩陣相乘得到的，計算所得的各運動學片段的主成分得分是下文K 均值聚類分析的數據基礎。

2.3 聚類分析算法

聚類分析是用距離來定義樣本之間的相似程度的一種數據分析方法，在做聚類分析時，各樣本之間的親密度對聚類分析的結果有重要影響。K 均值聚類法適用于大樣本數據分析，計算量相對較小，分類也更加合理。用MATLAB 編寫的均值聚類算法代碼對短行程聚類分析，根據對實際問題的分析確定分類數k，在進行計算時分別在各類中選擇出相應的聚點，再計算樣本數據與聚點之間的歐式距離，按照距離的大小進行聚類劃分，重復多次，直到分類結束。本次分析共重復20 次，得到較為穩定的聚點。聚類前后的數據統計如表4 和表5 所示。

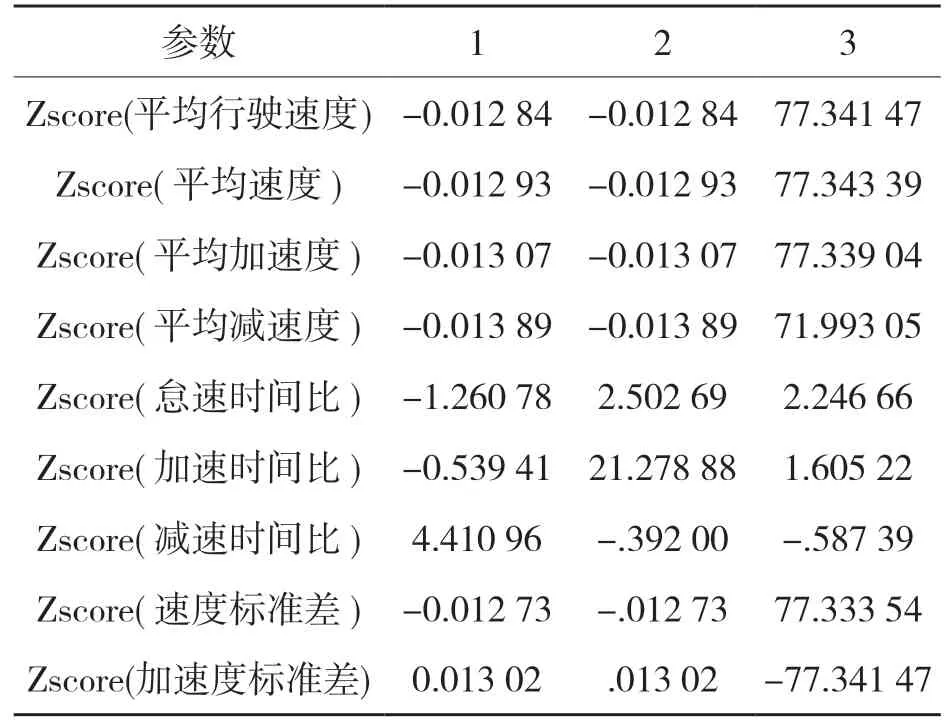
表4 初始聚類中心Tab.4 Initial cluster center

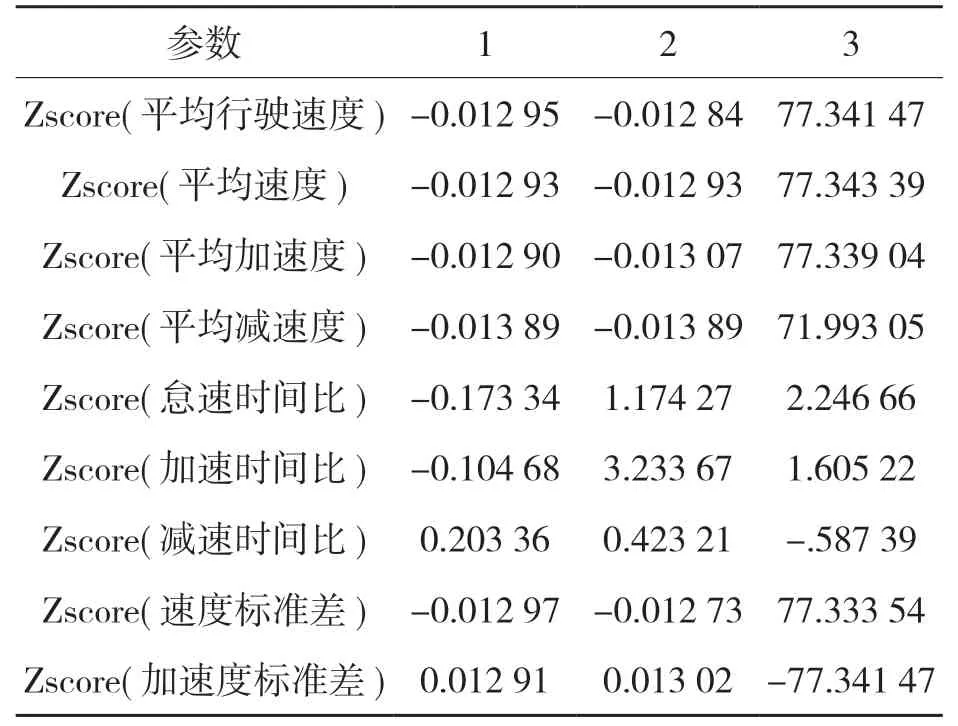
表5 最終聚類中心Tab.5 Final cluster center

將所有運動學片段分3 類進行聚類分析。聚三類分析的聚類結果如圖3 所示。

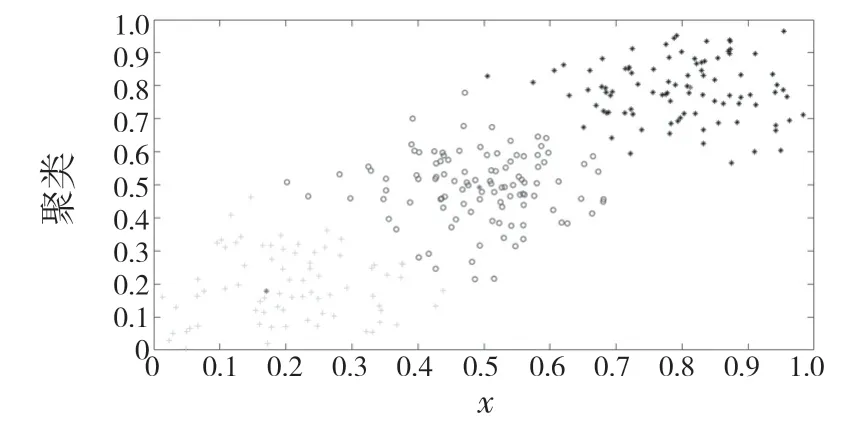
圖3 聚三類聚類結果Fig.3 Clustering results

3 行駛工況構建

聚類后形成了低速區間、高速區間以及介于高速區間和低速區間的中速區間三類數據，在每一類數據中選取短行程，組合成為確定時間長度的車輛行駛工況。在每一類中根據各個短行程與聚心的歐氏距離的大小選取短行程，計算各類短行程庫在整個短行程庫中所占的比例，結合需要構建的沈陽市乘用車城市道路行駛工況的持續時間，計算每類短行程在最終合成工況時的時間。計算公式如下：

計算得到最后構建工況時三類短行程的時間占比和各自所占的時長，如表6 所示。

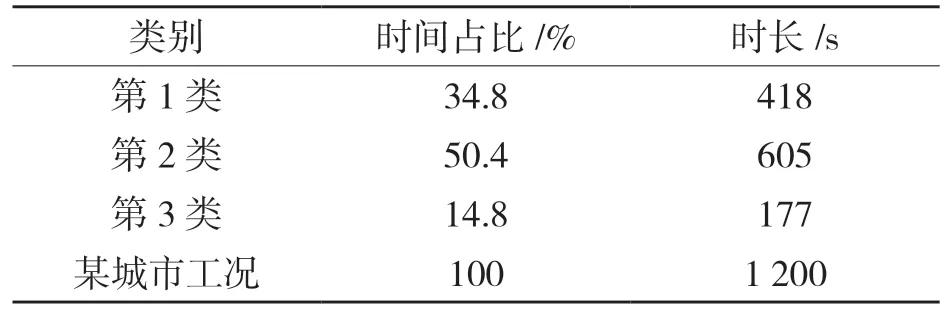
表6 各類工況時間占比Tab.6 Proportion of time under various working conditions

按3 類工況時間長度的計算結果挑選出每類中具有代表性的短行程作為聚類中心，按運動學片段與聚類中心的距離最小的原則在3 類候選工況中挑選出運動學片段，將挑選出的運動學片段分別合成反映擁堵交通狀況的低速工況、反映暢通交通狀況的高速工況和反映綜合交通狀況的綜合工況。汽車的加速度-時間曲線如圖4 所示，合成的高速工況、中速工況和低速工況的代表性行駛工況時間-速度曲線分別如圖5（a）、（b）、（c）所示。

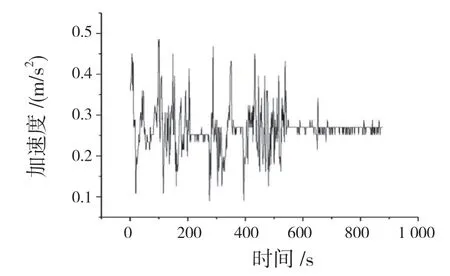
圖4 行駛工況加速度圖Fig.4 Driving cycle acceleration

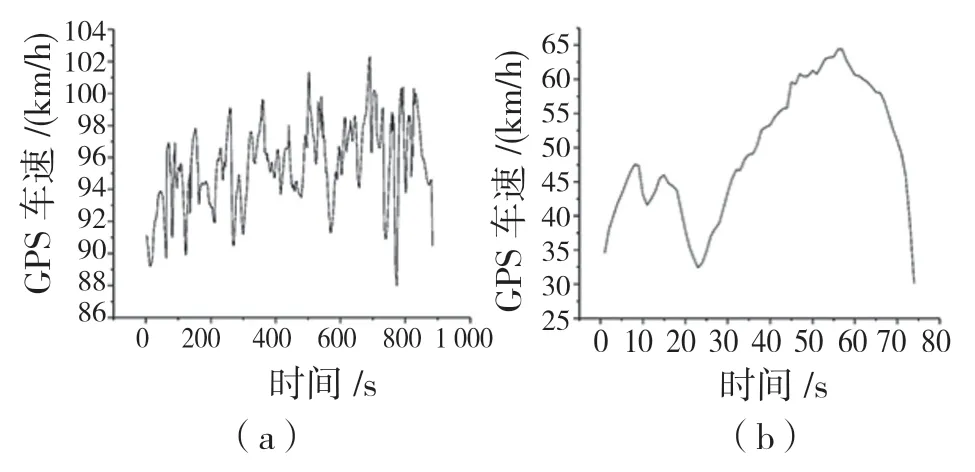
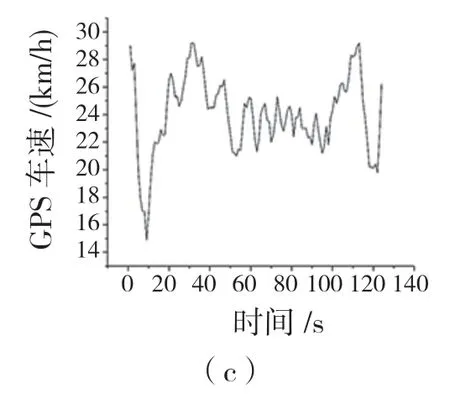
圖5 高、中、低速工況代表性速度-時間圖Fig.5 Typical speed-time diagrams for high,medium and low speed conditions

基于K-均值聚類分析結果中聚類中心的大小，篩選出高、中、低速的運動學片段，最后將3 個工況組合成900 s 的汽車行駛工況，合成后的汽車行駛工況如圖6 所示。

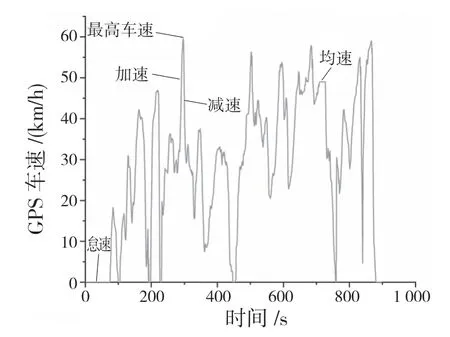
圖6 汽車綜合行駛工況圖Fig.6 Comprehensive vehicle driving conditions

4 誤差分析

本次汽車行駛工況是對實際車輛行駛數據進行分析來完成行駛工況搭建的，所以需要對構建工況的數據與原始數據之間的差異進行驗證。由于汽車行駛工況的構建是在對原始車輛行駛數據信息進行預處理后進行的，所以將對的特征值進行行駛工況的有效性驗證。均值插補法在處理小間斷點數據時具有比較好的可靠性，缺失值若是數值型的，就根據這個缺失值所在的其他對象值的平均值來進行缺失值的補全[12]。

汽車行駛工況的有效性驗證就是計算行駛工況的特征參數與預處理后數據特征參數的絕對誤差和相對誤差。對計算得出的誤差值進行分析，以驗證構建的行駛工況是否合理。誤差計算公式：

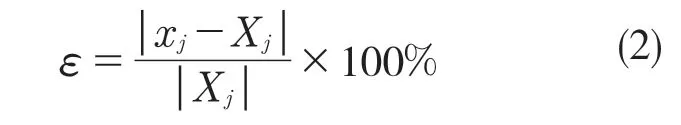
式中：ε——預處理后汽車行駛工況特征參數j和相應的原始數據之間的特征參數j 之間的相對誤差；xi——預處理后車輛行駛工況特征參數值；Xj——原始數據特征參數值。

計算得出各特征值之間的誤差值均小于10%，在合理范圍之內。由此可見，本文構建的汽車行駛工況與實際情況接近，合理且有效，能較準確地反映福州地區的汽車行駛工況。

5 結論

本文通過對大量的汽車行駛采集數據進行分析，采用主成分分析與聚類分析算法提取運動學片段，計算合成得出福州地區汽車行駛工況圖，反映出福州地區真實的車輛道路行駛狀況。計算得出各特征值之間的誤差值均小于10%，在合理范圍之內，能比較準確地反映該城市的汽車行駛工況，對車輛行駛工況的深入研究提供一定的理論參考。