關于一維量子散射中一些問題的簡單說明

應文祥，彭凱玥，曹 龍

(中國科學技術大學 化學物理系，安徽 合肥 230026)

一維方勢壘穿透是本科量子力學課程的一個重要內容.大多數教材采用求解定態(tài)薛定諤方程的方法[1-4].它本質是個一維定態(tài)散射問題(如無特殊說明，本文均指定態(tài)彈性散射)，我們也可以求解一維Lippmann-Schwinger方程——這是一種更普適的方法，理論上可以程序化解決任意形狀勢壘的一維散射問題.早在2001年，陸曉[5]就補充了這種思路，并通過迭代求出了反射、透射概率幅，但是其過程的數學存在瑕疵.王琴惠[6]在2004年給出的求解過程數學上沒有問題，但透射、反射系數項中仍含有ψ(x)，須通過代入試探解來求解實際問題.

鑒于前人對一維散射問題處理方法的一些理解誤區(qū)，本文給出了較為清晰的數學推導和說明.簡單討論了迭代法求解一維Lippmann-Schwinger方程的手續(xù)，指出前人的錯誤.

1 一維散射問題常見處理手法的簡單討論

一維散射問題的定態(tài)薛定諤方程為

(1)

最常規(guī)的思路就是直接求解一維定態(tài)薛定諤方程.參考文獻[1]中列舉了很多種一維可解勢——對于這類勢函數，可以解析求解.但局限性是，這不是一種通用的方法.對復雜的勢函數V(x) 很難解析求解薛定諤方程.例如一維有限深方勢阱[2]，薛定諤方程為超越方程，無法寫出解的顯示表達式.

第二種思路仍然是處理微分方程，但略有差異.對薛定諤方程做變量代換：

(2)

則薛定諤方程形式簡化為

(3)

可以發(fā)現這是個二階變系數齊次線性方程，并且屬于下面這種類型：

y″+r(x)y=0

(4)

因此只要能夠一般化處理 (4) 這種類型的二階變系數齊次線性方程，寫出通解并代入邊界條件，則問題可以完全解決.基于這種思路的相關研究也有不少[7-10]，但是依舊存在困難和局限性，有時需數值求解[8].能夠寫出通解的僅是一些特殊情形[9,10].

第三種思路見參考文獻[4].作者Franz Schwabl把任意形狀勢壘分成無窮多個窄的一維方勢，并且認為總透射系數是這些小方勢的透射系數之積.這是一種粗糙的數學處理，難以保證計算的可靠性.這里指出兩點問題.其一，Franz使用如下近似公式 (5) 處理每小段的一維方勢：

(5)

但是該近似是對于高且寬的勢壘才成立的[2].其二，按照這種模型，可能存在粒子在勢壘內部經過多次反射、透射后最終通過勢壘的情況.

還有不少其他處理思路，例如相移分析[11,12]等，還有人開發(fā)了處理一維耗散問題(非彈性散射)的方法[13]，在此不一一列舉和討論了.

通過Lippmann-Schwinger方程來處理一維散射問題是一種很好的思路[5,6,14,15].方程可以基于式 (3) 通過格林函數方法導出[6,15,16]，這里不再花費篇幅介紹.一維的Lippmann-Schwinger方程形式如下

(6)

其中G(x,x′)為一維非齊次亥姆霍茲方程邊值問題的格林函數解：

(7)

把代換的變量代回，式(6) 也可以寫成如下形式：

(8)

此方程為積分方程，無法直接求解，一般要借助于迭代算法.記

(9)

并把積分寫成分段式以去掉絕對值

(10)

ψ(x) 為全空間上的解.考察ψ(x) 的漸進行為,當x→ +∞ 時， 有

(11)

2 對參考文獻 [5]誤區(qū)的說明、拓展討論

2.1 迭代法和代入試探解法

參考文獻 [5] 給出波函數的漸進行為是正確的，對應一維散射問題的邊界條件.但是，作者錯在使用漸進解迭代，混用了迭代法和代入試探解法.作者首先使用迭代法，并認為經過多次迭代后的真實解就是

ψ(x)=sAeikx

(12)

(見參考文獻 [5] 式 (19) ，其中s為透射概率幅)，這是錯誤的.這種做法就相當于代入試探解，但是這個解的形式又太簡單，不能包括x軸上波函數的全部信息——式 (12) 形式的波函數僅僅能夠描述無窮遠處波函數的行為，而Lippmann-Schwinger方程中的ψ(x)為全空間的波函數，導致錯誤.例如可以檢驗，參考文獻 [5] 給出的理論無法對一維方勢散射給出正確結果.

一般來說，迭代法和代入試探解法都可以解方程，但是參考文獻 [5] 的作者此處混淆了這兩種方法.如果迭代，就不能隨意舍去波函數的重要信息，要考慮全空間范圍，從低階到高階一步步進行，最終會收斂于真實解；如果代入試探解，那么為得到正確結果，這個試探解必須包括該束縛定態(tài)下所有可能的物理態(tài)——即：全空間范圍內的解，包括勢壘內部、外部，進而確定試探解的前系數.如前文所述，如果僅僅代入無窮遠處的漸進解，就會缺失大量信息，特別是如圖1所示勢壘內部的波函數的真實態(tài)——這是問題的難點.

圖1 散射問題圖示說明[17]

迭代法求解Lippmann-Schwinger方程時，迭代次數對應玻恩近似的階數[18].并且，一維散射問題引入玻恩近似將不受“低能散射”條件[18]的束縛，因為根據彈性散射問題的邊界條件，無窮遠處入射波和透射波的波矢相等，因此不存在高維情形時由于波矢方向變化帶來的額外的相位差.高階玻恩近似能夠較好地描述波函數的行為.后面我們給出的例子將說明這一情形，在高能段玻恩近似的結果更好.而低能段可能出現由于截斷導致的紅外發(fā)散.

2.2 S矩陣，反射、透射系數

一般在高維散射問題中，問題可化為求解時間相關的散射S矩陣.求解S一個很好的方法是微擾展開法，可以用戴森級數加以表示[19].基于此，本文一位作者曾提出由式 (11) 進行迭代，并引入相應正規(guī)乘積算符[19]——位置編序算符加以表示以統(tǒng)一積分上限

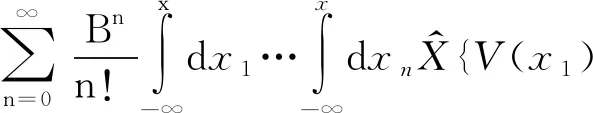
V(x2)…V(xn)}≡

(13)

定態(tài)問題不含時，位置算符兩兩對易，所以去掉編序算符.這種方式給出的s也是錯誤的，錯在用近似了的積分方程迭代，因此只能給出極限形式的s，而真實的s可能會非常復雜.事實上式 (13) 就是一維情形的s的戴森級數表示，只是把時間序列改為空間序列(無本質差別，但時間編序不能直接去掉編序算符).

繼續(xù)考察一維散射的反射、透射系數.假設粒子從一個方向入射

(14)

其中s為透射概率幅，r為反射概率幅.對于給定的定態(tài)勢函數，r、s均為復常數.參考文獻 [5] 在原文式 (13) 處給了兩者之間存在關系式s= 1 +r.這也是錯誤的.r、s之間的關系由波函數的邊界條件確定.例如一維δ勢、一維階梯勢等，x= 0 的左側和右側分別對應波函數的兩個漸進解，在此處根據連續(xù)性條件令x= 0，即可直接得出s= 1 +r.但是對于復雜一些的情形例如一維方勢散射，此關系式不再成立，由更復雜的邊界條件給出r、s之間的關系.筆者猜測，作者此處是想尋找r、s與更高維量子散射中R、S矩陣之間的聯系.量子散射的S矩陣是描述無窮遠處散射態(tài)的厄米算符，反應矩陣R是人為引入的，定義兩者關系R+ 1 =S，是為了更方便地導出躍遷幾率[17,20].但是退化為一維情形時，R、S并不對應著反射、透射概率幅r、s.一維的S作用在入射初始態(tài)上，仍然將給出所有的散射態(tài)——包括反射波和透射波，而不僅僅是透射概率幅s所描述的透射波.而一維情形中彈性散射的粒子數守恒關系T+R= 1是根據概率守恒得證的[21].

2.3 勢函數積分的斂散性

由于代入的是漸進解，式(13) 只是正確的s的表達式的一部分，其中含有對勢函數V(x) 的多重積分.為使得對應的s有意義，我們不得不考慮該積分的斂散性問題.例如對于一維冪函數勢：

(15)

當冪指數ν在 (0 ,1 ] 內時積分發(fā)散，迭代發(fā)散，無法給出透射概率幅.我們在構造勢函數時，要構造正規(guī)勢函數，例如盡量避免涉及無窮奇點等.總之使得s是有意義的.另外，對于這類因為有無窮間斷點導致積分發(fā)散的情形，張永德給出了很好的觀點[22]：這種情形是人為的定義造成的，物理實際上并不存在，我們不必過于糾結由于這類非正規(guī)勢函數性質帶來的不必要的困惑.

推廣到更一般的情形，如果使用微擾展開來求S矩陣，在把全哈密頓量分為自由粒子部分哈密頓量H0和相互作用部分V時，就涉及H0選取的問題[19].散射理論中H0并非通常微擾意義下的，選取的H0及其本征態(tài)要求包含所有可能存在的物理態(tài)，例如平面波、勢壘中的束縛態(tài)等.正如S.Weinberg在其《量子場論》第一卷中指出[19]，需要使得H0和全哈密頓量H有相同的頻譜，H中的任何相關束縛態(tài)都應該像一個基本粒子一樣被引入H0.由此H0的譜中也可能包含一些束縛態(tài)(非平面波)成分；由此也要求了勢函數滿足相關條件,例如一定的漸進行為等等.

3 應用：一維δ勢散射的迭代法求解

一維δ勢散射問題，代入試探解的方法可見參考文獻 [6]，此處對迭代法舉例說明.勢函數：

V(x)=λδ(x)

(16)

λ為參數.把式 (16) 代入式 (10) ，并根據δ函數的積分性質得

(17)

下面使用迭代法求解，迭代關系為

(18)

0 階近似為自由平面波：ψ(0)(x)=Aeikx.此時0 階透射概率幅：s(0)=1.

把自由平面波ψ(0)(x)=Aeikx代入式 (18) 右邊即得一階玻恩近似結果：

(19)

s(1)=λB+1

進一步迭代可以給出

(20)

s(2)=λB(λB+1)+1

等等.可以注意到透射概率幅有遞推關系：

s(n)=λBs(n-1)+1

(21)

當n取無窮大時s已經收斂.把B代換回去，可以反解出一維δ勢散射的透射概率幅為

(22)

從而透射系數為

(23)

與文獻中代入試探解得到的結果[6,14]完全一致.

下圖2 給出了透射系數的前幾階玻恩近似結果，并與解析解進行比較.

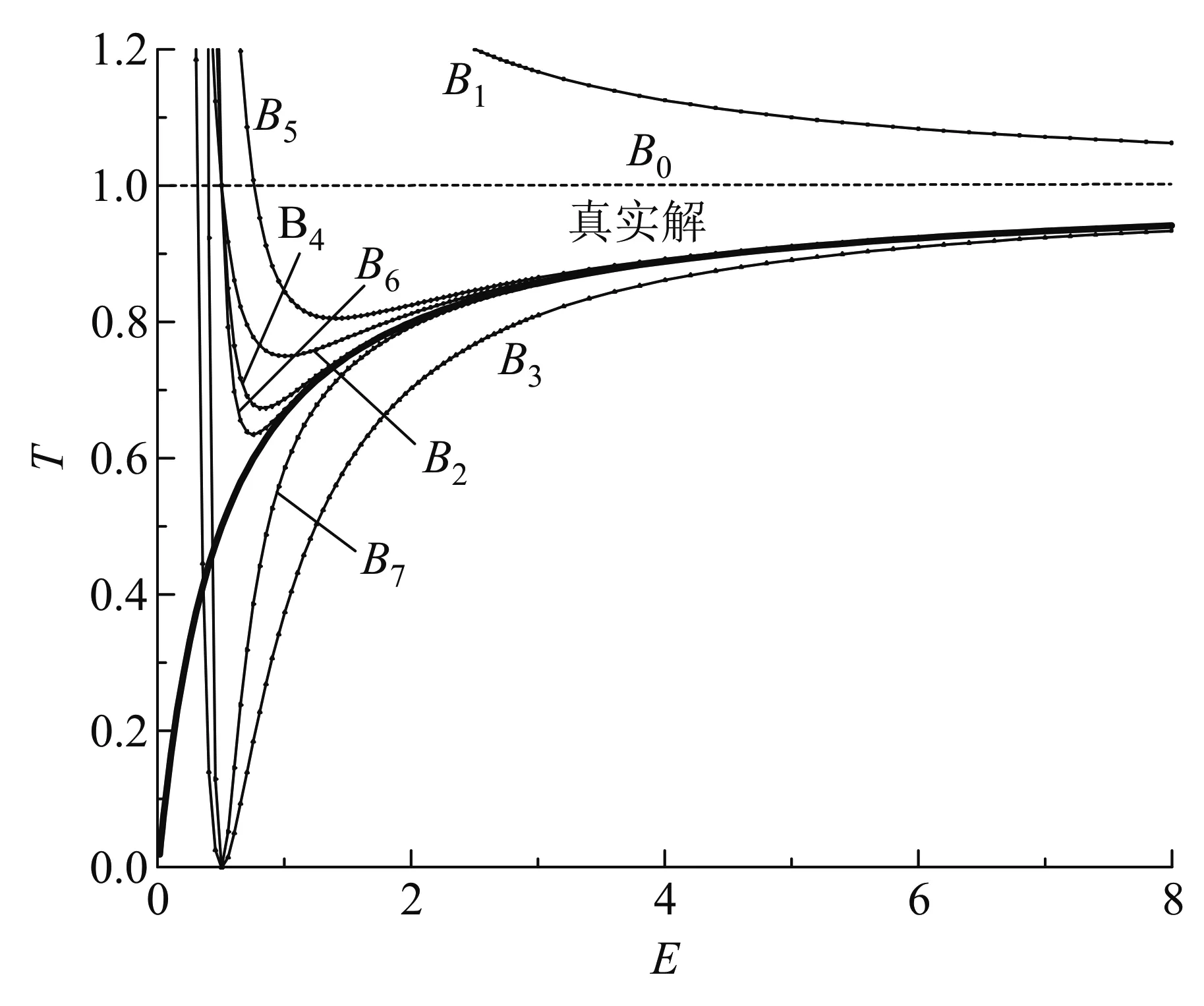
圖2 δ勢散射問題的前7階玻恩近似下透射系數隨入射能量變化情況，以及與解析解的比較.Bn表示第n階玻恩近似的結果，加粗線條為解析解.這里相關參數取自然單位制：λ= 1,m=1,?=1

對于更為復雜的勢函數例如一維冪函數勢[5]、一維高斯型勢壘[8]可借助計算機通過上述固定步驟數值求解.

4 總結

解決一維定態(tài)勢散射問題，幾種方法各有優(yōu)劣.對于勢函數簡單的情形，例如一維方勢、一維階躍勢等，我們容易給出正確的試探解的形式，此時直接代入試探解求解定態(tài)薛定諤方程更方便；對于勢函數復雜而無法解析求解的情況，考慮迭代法，數值求解 Lippmann-Schwinger方程.