受迫振動非線性特性的教學拓展

丁紅勝，王佳曦，張師平，董軍軍

(1. 北京科技大學 數理學院應用物理系，北京 100083；2. 北京科技大學 自然科學基礎實驗中心，北京 100083)

振動是一種普遍存在于客觀世界的物質運動形式，系統在周期性外力的持續作用下的振動即為受迫振動[1]．波耳共振儀是高校物理實驗教學中研究受迫振動運動規律較為普遍的儀器，也是學者探討較多的實驗項目[2-4]．實驗測量中，儀器的軸承摩擦和彈簧非線性效應的影響是造成實驗數據偏離預期的主要因素．如果在受迫振動的分析中考慮這兩種因素的影響，則非常有助于學生理解實驗原理和結果偏差．本文基于受迫振動常規實驗，延伸探討其非線性特性，通過Matlab數值分析的方法來研究杜芬方程的混沌特性，以此提高學生對受迫振動的認知，并加深對其非線性特性的理解．

1 受迫振動

1.1 受迫振動方程

波耳共振儀[5](如圖1所示)的擺輪可在彈性力矩作用下自由擺動，若同時加上阻尼力矩和驅動力矩，擺輪可做受迫振動．

1. 光電門A；2. 長凹槽；3. 短凹槽；4. 銅制擺輪；5. 搖桿； 6. 蝸卷彈簧；7. 機架；8. 阻尼線圈；9. 連桿；10. 搖桿調節螺絲； 11. 光電門B；12. 角度盤；13. 有機玻璃轉盤；14. 底座； 15. 彈簧夾持螺絲；16閃光燈圖1 波耳共振儀的結構示意圖[5]

(1)

式中，J為擺輪的轉動慣量，-kθ為彈性力矩，k為彈簧的勁度系數，M0為驅動力矩的幅值，ω為驅動力的角頻率．

(2)

當mcosωt=0時，即在無周期性外力矩作用時，式(2)為阻尼振動方程；當阻尼系數為零，即無阻尼時，式(2)為簡諧振動方程，ω0即為振動系統的固有頻率．

方程(2)的通解為

θ=θ1e-βtcos(ω1t+α)+θ2cos(ωt+φ)

(3)

通解含有兩個部分：θ1e-βtcos(ω1t+α)表示阻尼振動，隨著時間的演化，振動會逐漸衰減，直至忽略不計；θ2cos(ωt+φ)表示簡諧振動，驅動力矩持續對擺輪做功，振動系統接收驅動力所傳送的能量，使振動系統最終達到一個穩定的狀態．

振幅為定值，

(4)

系統相位差為

(5)

由式(4)和式(5)可看出，穩定振動時，驅動力的幅值M0、阻尼系數β、驅動力的頻率ω(或驅動力周期T)和系統固有頻率ω0(或固有周期T0)4個參量共同決定系統振幅和相位差的大小，與振動的起始狀態無關．

(6)

可以看出，阻尼系數越小，驅動力的角頻率越接近系統的固有角頻率，振動幅值也越大．

1.2 阻尼系數、固有周期、固有頻率的測量

實驗中通常選擇阻尼開關位置為2，將波耳共振儀有機玻璃盤上零度標志線對準0°，用手將擺輪轉動至140°～150°之間，放手后控制箱會自動連續記錄擺輪完成阻尼振動10次的振幅θ0～θ9．數據如表1所示．

表1 阻尼系數測量數據

選擇“自由振蕩”進行測量，將有機玻璃盤上零度標志線保持在0°，用手將擺輪轉動至140°～150°之間，放手后記錄每次振動振幅值及其相應周期，并計算相應頻率值．數據如表2所示．

表2 振幅、周期、頻率關系數據

2 受迫振動方程非線性修正

2.1 彈簧非線性效應

一般情況下，可以認為彈簧的勁度系數k為常數，但是在上述彈簧自由振動的實驗中，通常隨著振幅的減小，振動系統固有周期會逐漸增大，這意味著振動系統的彈性回復力隨著振幅的減小而減弱[2]．因此不妨假設彈簧的勁度系數為振幅的函數k=k(θ)，則回復力矩為

Fk=k(θ)θ

(7)

將Fk=k(θ)θ進行泰勒展開至一階項，

(8)

(9)

2.2 軸承摩擦效應

軸承摩擦效應普遍存在于定軸轉動的運動中，當軸承轉動速度較小時軸承靜摩擦力較大，而當轉速達到一定臨界值后，軸承摩擦力將保持穩定[6]．

實驗發現，軸承摩擦力隨軸承角速度的變化率較緩，因此可采用二次函數的形式來描述軸承摩擦力矩隨角速度的關系

(10)

其中，固定系數B>0，C>0，在此情況下，即表明摩擦力矩隨角速度的增加而緩慢降低．

2.3 阻尼振動方程非線性修正

綜合彈簧的非線性效應與軸承摩擦效應對振動方程的修正，可以得到修正后的阻尼振動方程為

(11)

(12)

式(12)即為非線性項修正后的阻尼振動方程，是一個待定系數的二階微分方程．

在此情況下，基于Matlab軟件，用數值方法計算其數值解，通過多次給定a、b、c的數值進行模擬計算，擬合阻尼振動實驗所測得的數據．

(13)

利用Matlab軟件內置的ode45函數，根據四階龍格-庫塔法，多次變步長數值積分，可以得到，當待定系數滿足a=0.014,b=0.002,c=0.005時，數值方法解得的阻尼振動方程與實驗數據擬合的最為接近，特別是在振幅為90°～140°時，彈簧形變較大，彈簧非線性效應較為明顯的區域．

圖2中指數曲線為阻尼振動的振幅-時間實測數據的擬合曲線，周期性曲線為非線性微分方程的數值解．

圖2 阻尼振動數值積分與擬合曲線

2.4 受迫振動方程非線性修正

在修正后的阻尼振動方程(12)的右邊加上一個周期性力矩，即為受迫振動方程，

(14)

該方程中m為未知參量，需要通過實驗儀器進行數據測量加以確定．

選取“阻尼2”檔位，打開電機，設定在某一轉速，當觀察到擺輪的受迫振動周期與電機的周期趨于一致時，即受迫振動達到穩定時，開始測量．讀出每次擺輪受迫振動的幅值θ和驅動力矩每10次振動周期10T，利用頻閃法測量擺輪受迫振動的位移與驅動力之間的相位差φ，并記錄此時電動機的轉速值，結果如表3所示.

表3 幅頻特性與相頻特性測量數據

至此獲得了在一定情況下，受迫振動動力學方程的全部參量：ω0=3.775 rad·s-1，β=0.081，m=1.02，a=0.014，b=-0.002，c=0.005．

(15)

把上述一階微分方程組輸入程序，利用數值積分求解其動力學特性，結果如圖3所示．

圖3 系統時間響應與相平面曲線

圖3中左側為受迫振動系統的時間響應曲線，右側為系統的相平面曲線．受迫振動系統的時間響應曲線表示了振動振幅隨時間變化的特性，可以看出，隨著振動時間的增加，振動頻率逐漸穩定，振幅逐漸增加直到最大值并且保持穩定．

受迫振動系統的相平面曲線圖表示了速度隨振幅變化的關系．可以看出隨著時間的增加，速度與振幅也會趨近一個穩定狀態．

如果改變其中的一個參量，例如將與彈簧非線性效應相關的參數a從0.014調整為10，采用同樣的方法對系統進行數值分析，得到的結果如圖4所示．原本穩定的受迫振動系統在振動后期開始出現一定的隨機運動，即混沌現象．

圖4 系統時間響應與相平面曲線

基于波耳共振儀的受迫振動，由于其振動方程中涉及的非線性項偏多，不利于定性和定量分析受迫振動系統中的混沌現象，因此可以選擇典型的非線性受迫振動方程——杜芬方程進行探討．

3 受迫振動方程的混沌

3.1 杜芬方程

振動問題中的很多數學模型都可以通過轉化為杜芬方程來進行研究和分析，杜芬方程是研究和分析某些非線性動力學系統的基礎．

杜芬方程[7]的標準形式為

(16)

其中，δ>0，g(x)是含x3項的函數，f(x,t)是周期性函數．

標準化后的杜芬方程稱之為杜芬系統．杜芬系統是一類從簡單受迫振動的物理模型中歸納出的非線性振動系統模型，形式簡潔，具有代表性，其應用范圍十分廣泛．許多動力學過程都與杜芬系統的模型極其相似，比如化學鍵的斷裂、建筑結構的震顫和輪船的橫搖運動、電路周期振蕩、電路信號檢測、電路系統模擬分析和電路的故障檢測等等．

3.2 硬彈簧型杜芬方程

杜芬方程一般可以分成四種基本類型，可以選取其中的硬彈簧型杜芬方程[8]進行探討，

(17)

將式(17)轉化成一階微分方程組：

(18)

其中ω、f、a、β、c為可變參量．

給定不同的初始條件，利用數值計算的方法來分析硬彈簧型杜芬系統的受迫振動．

當振動時間為300 s時，結果如圖5所示，從上至下依次是不同f取值下的系統時間響應圖、系統相平面軌跡圖、系統功率密度譜．

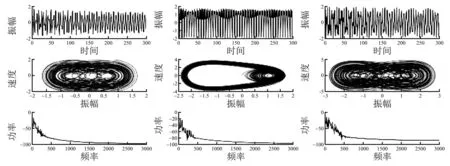
圖5 系統時間響應、相平面軌跡、功率密度譜隨f值的演化

由圖5可以看出，隨著系統參量f的變化，系統逐漸由周期性運動進入混沌狀態．

3.3 杜芬方程的混沌

從圖5的相平面軌跡圖可以看出，系統從只有一個相對穩定的平衡位置(原點)，逐漸變為具有兩個相對平衡的位置(焦點)，這體現了無序混沌狀態中存在一定程度上的有序特性．相平面軌跡圖中相對平衡位置發生改變的同時，相軌跡也從圓形逐漸轉化為類似于莫比烏斯環的橢圓形狀．進一步推測，系統會擁有兩個相對平衡的焦點，相軌跡圍繞這兩個焦點運動，而且可將這兩個焦點類比為三維非線性系統中奇異吸引子[9]，如圖6所示．

圖6 奇異吸引子

奇異吸引子是混沌系統中獨有的一種吸引子，也被稱之為混沌吸引子，它代表著混沌狀態中的一種定態．具體表現在系統從任一初始狀態開始，最終都會被奇異吸引子吸引到相空間中的某一特定區域．奇異吸引子與一般吸引子有所區別，當混沌狀態的軌跡線進入奇異吸引子之后，軌跡線并不會像一般吸引子一樣，吸引軌跡線繼續圍繞其運動，最終形成一個相對封閉的圖形，而是會讓兩條接近的軌跡線發生指數分離．從系統外部看，奇異吸引子是在聚集軌跡線；從系統內部看，是軌跡線發散的過程．奇異吸引子常常成對出現，兩個奇異吸引子同時對軌跡線的作用，共同構筑了混沌系統一定程度上的有序性．

圖7 從左至右分別為f=1, f=3, f=5時的相空間軌跡線

從圖7可以看出，杜芬方程中的兩個焦點在含有時間項的坐標下，展開成了兩條軸線，體現了其時間平移不變性，參量f的變化引起相空間軌跡明顯改變，表明混沌系統對參量具有很強的敏感性，但在速度-振幅的相平面軌跡圖中，兩個焦點是穩定的，不隨時間發生變化，這與奇異吸引子的性質非常類似．

4 結論

基于波耳共振儀受迫振動實驗，探討其中的非線性影響因素，對阻尼振動方程進行修正，考慮軸承摩擦和彈簧非線性效應，結合Matlab數值計算結果與波耳共振儀實測數據，確定波耳共振儀系統的非線性項參數，分析其非線性效應．通過引入非線性理論的思想和數值分析的計算方法，有助于學生準確認知實驗現象，加深對實驗原理的理解．

為了豐富實驗教學內容，引入彈簧型杜芬方程，分析其非線性特性，利用數值計算方法探討受迫振動模型進入混沌狀態的條件及其運動特性．受迫振動是否會進入混沌狀態，可以根據系統響應時間曲線(振幅-時間)、系統相平面曲線(速度-振幅)和功率密度譜曲線(功率-頻率)綜合判斷．如果受迫振動做周期運動，其響應時間曲線會呈現規則的周期性，其相軌跡圖具有極限環的特性，其功率圖譜峰值呈現離散的狀態；如果系統進入混沌狀態，其時間曲線會具有無規則的、類似于噪聲的特性，其相平面曲線在有限區域內是無周期性的，隨著振動時間的延長，其軌跡線會逐漸鋪滿整個區域，功率圖譜含有多個峰值；如果系統的響應時間曲線和相平面曲線在上述兩種情況之間，則功率圖譜呈現離散狀態，系統做的是擬周期運動，如果改變它的系統參量或者初始條件，則有可能轉變為周期運動或混沌運動．一般情況下，受迫振動受非線性效應影響越大，最終進入混沌狀態的可能性越高．