參數微擾法中基態能量與近似級數的關系

吳 鋒，孟麗娟

(鹽城工學院物理系，江蘇 鹽城 224051)

參數微擾法通過引入參數重構量子體系哈密頓量中的無微擾項和微擾項，削弱了微擾項的影響，提高了本征能量的準確性，擴大了微擾法的適用范圍[1-8].目前，參數微擾法已經成功用于研究三體類氦原子、四體類鋰原子和五體鈹原子體系[1-6]，這些工作促進了對電子對核屏蔽效應的認識，加深了對電子間相互作用、泡利不相容原理和全同粒子交換對稱性的理解.

用參數微擾法精確計算體系能量，有時需要計算到二級甚至多級近似，那么就會遇到和利用微擾法一樣存在的困難，即計算包含著無窮項求和的能量修正項.鑒于此，文獻[3]利用類氫原子s態波函數構造氦原子的近似波函數，巧妙實現了對氦原子四級近似基態能量的精確計算，理論值與實驗值的絕對誤差為0.0049 Hartree.但不足的是，該文在構造波函數時犧牲了電子的空間交換對稱性，而且計算的氦原子基態能量與采用的近似級數間的關系尚不清晰.為此，本文在構造滿足空間交換對稱性的近似波函數的基礎上，對參數微擾法算出的氦原子基態能量與近似級數間的關系進行了探究，以期為利用參數微擾法精確計算量子體系本征能量提供借鑒.

1 理論和方法

氦原子的非相對論哈密頓算符(原子單位):

(1)

其中

(2)

(3)

式中r1和r2為原子中兩個電子到核的距離，r12是兩個電子間的距離，Z為核電荷數，σ為反映電子對核屏蔽效應的微擾參數.

根據微擾論，氦原子的零級近似基態能量:

E(0)=-σ2

(4)

基態能量的第i(i=1,2,3,)級修正[1,9]:

E(i)=〈ψ(0)|H′|ψ(i-1)〉

(5)

其中，ψ(0)為零級近似波函數，ψ(i)為第i級修正波函數，與ψ(0)正交.根據式(2)結合氦原子特征，選取類氫原子的ns (n=1,2,3,)態歸一化波函數:

(6)

(1F1為合流超幾何函數)構造ψ(0)和ψ(i)：

ψ(0)=ψ1s(r1)ψ1s(r2)

(7)

(8)

氦原子的多級近似基態能量和波函數分別為:

E=E(0)+E(1)+E(2)+E(3)+…

(9)

ψ=ψ(0)+ψ(1)+ψ(2)+…

(10)

由式(7)和式(8)可知，ψ自動滿足空間交換對稱性.E和ψ中參數σ由基態能量取最小值確定.

2 計算結果和討論

利用Mathematica軟件的符號計算功能，得到氦原子各級近似基態能量E的解析表達式(限于篇幅未列出)，它們是參數σ的函數.在討論近似級數對E值的影響時，既可以通過對各級近似基態能量分別取最小值確定σ，也可以通過由某級近似基態能量取最小值確定σ，然后在各級近似計算中保持不變.下面分別進行討論.

2.1 σ分別由各級近似能量取最小值確定

表1列出了2級至12級近似基態能量E，參數σ，以及E與實驗值[10](-2.903386 Hartree)的絕對誤差|ΔE|.可以看出，E隨著近似級次i的增加而減小.圖1進一步給出了各級近似基態能量E相對前一級基態能量的改變量.可見，E的改變量隨著i的增加越來越小，逼近于零.

表1 氦原子i級近似基態能量E及其與實驗值的絕對誤差|ΔE|(原子單位)

其次，從表1末列數據，可以看出，|ΔE|隨著i的增加先是減小，i=4時達到最小，然后又逐漸增大.這表明，氦原子基態能量與實驗值的絕對誤差隨著i的增加存在一定起落.這與文獻[3]提出的|ΔE|隨著i的增加越來越小的論斷不同.因為|ΔE|存在起落，所以需要合理選擇近似級數，提高氦原子基態能量計算值的精確性.例如，表1中4級近似的|ΔE|僅為0.0039 Hartree.

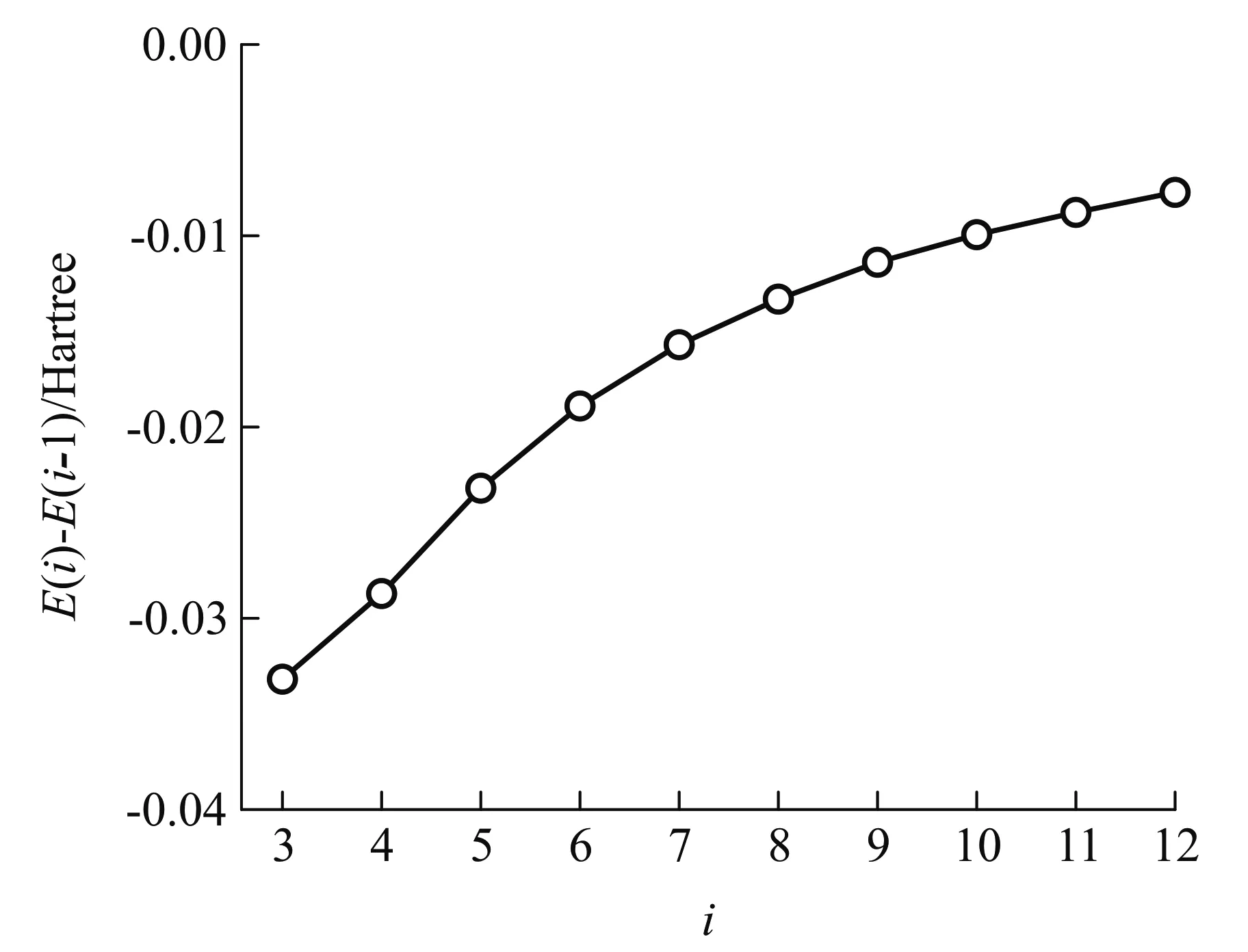
圖1 i級近似基態能量相對前一級基態能量的變化

2.2 σ由某級近似基態能量取最小值確定，并在各級近似計算中保持σ相同

將表1中各級近似得到的σ數值作為固定值，分別同時代入氦原子2級至12級近似基態能量表達式，所得數值結果按從左到右順序分別列于表2.分析E的每一列數據可知，E隨著i的增加仍有與2.1節相同的變化規律，即逐漸減小，改變量越來越小(如圖2)，與實驗值間的絕對誤差|ΔE|有起落.另外，σ的變化對|ΔE|的起落產生影響.所以，除了選取合適的近似級數計算基態能量，還需選取合適的近似級數確定σ，才能得到更為精確的氦原子基態能量.例如在σ=1.3165時，4級近似基態能量-2.9027 Hartree，與實驗值的絕對誤差小至0.0007 Hartree，結果相當精確.

表2 σ恒定時的i級近似基態能量(原子單位)

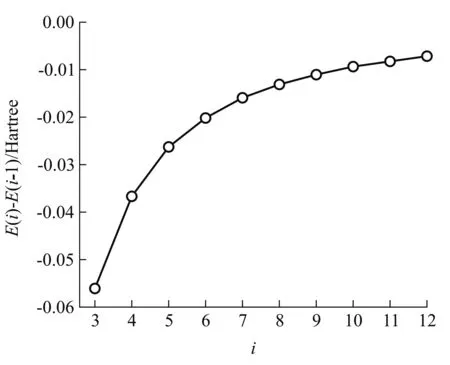
圖2 在σ=1.3165時，i級近似基態能量相對前一級基態能量的變化

3 結束語

在構建滿足空間交換對稱性波函數的基礎上，利用參數微擾法對氦原子基態能量進行了計算，并根據微擾參數的兩種確定方式，分別對基態能量與近似級數的關系進行了分析.研究發現，氦原子基態能量隨著近似級數的增加，逐漸降低，改變量越來越小，基態能量與實驗值的絕對誤差存在一定起落.選擇合適的近似級數確定微擾參數及基態能量，對提高氦原子基態能量計算值的精確性具有重要作用.