電動汽車多自由度整車建模與仿真分析

栗振闖，冉濤，孫琛，蘇丹丹

（1.河北大學 質量技術監督學院，河北 保定 071002；2.保定長安客車制造有限公司，河北 定州 073000）

前言

隨著計算機技術和汽車動力學理論的發展，虛擬樣機作為一項以動力學理論為基礎，利用計算機進行整車建模與仿真分析的新興概念，在縮短整車設計周期、及時排查汽車安全問題和降低車輛研制成本等方面得到廣泛應用[1]，尤其在當下新型電動汽車技術的研制中發揮著重要作用。

汽車虛擬樣機技術開發的核心內容是車輛動力學。有關車輛動力學的研究，國內外學者均作出了大量貢獻，如國內的郭孔輝院士針對兩軸車輛討論建立了 12自由度非線性模型[2]；密歇根大學的W.Riley.Garrot建立了具有十七個自由度的數字化模型[3]；日本東京大學的Sakai Shin-ichiro等人采用不考慮垂向運動的7自由度整車模型完成了電動汽車動態驅動/制動力分配的研究[4]；遼寧工業大學李剛等人基于 Matlab/Simulink 建立了 15自由度四輪輪轂電機電動汽車模型[5]；以及吉林大學靳立強等人基于四輪獨立驅動電動汽車建立了18自由度四輪獨立驅動電動汽車動力學模型[6]。

然而，以上有關車輛動力學建模的研究，僅考慮了提升模型的復雜度，忽略了對不同自由度模型的橫向對比分析。因此本文利用Matlab/Simulink建立了經典的2自由度、7自由度和10自由度整車動力學模型進行橫向對比，探求不同自由度整車模型的適用工況。

1 多自由度整車動力學模型

1.1 二自由度整車模型DOF_2的建立

根據簡化的二自由度整車模型在車輛坐標系中的運動狀態，建立整車的橫向與橫擺運動微分方程如下：

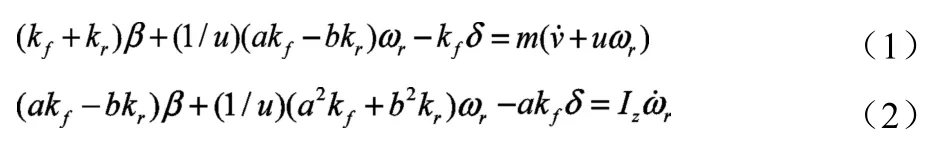
式中：β為質心側偏角（rad）；δ為前輪轉角（rad）；u為整車質心縱向速度（m/s）；ωr為整車橫擺角速度（rad/s）。

在 Matlab/Simulink中搭建線性二自由度整車動力學模型如下：

圖1 二自由度整車Simulink動力學模型

1.2 七自由度整車模型DOF_7的建立

車輪是車輛與路面之間進行力學傳遞的主要部件，作用于其上的縱向力、側向力和垂向載荷等對汽車的操穩性有著重要影響。基于輪胎魔術公式，增加四個車輪的滾動和簧上質量沿車輛坐標系x、y軸的移動與繞z軸的橫擺運動，建立了7自由度整車模型（DOF_7）。

式中：x軸選取汽車的縱向速度方向，并規定前進為正；y軸選取汽車的橫向速度方向，規定向左為正；z軸則通過汽車的質心豎直向上，有關橫擺角速度及質心側偏角等分析以逆時針方向為正。

車身的運動學方程如下：

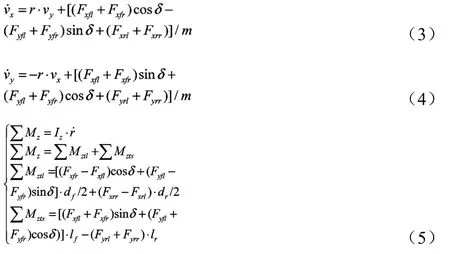
車輪的動力學方程如下：

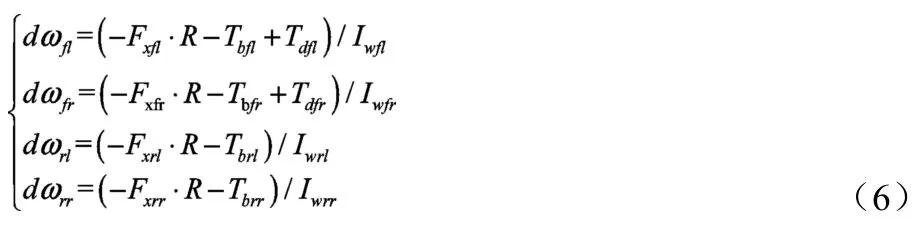
式中：Tdfl、Tdfr為兩前輪驅動轉矩（N·m），Tbfl、Tbfr、Tbrl、Tbrr為四個車輪制動轉矩（N·m），ωfl、ωfr、ωrl、ωrr為四個車輪轉動角速度（rad/s）；vx為整車縱向速度（m/s）；vy為整車橫向速度（m/s）；Fxfl、Fxfr、Fxrl和Fxrr分別為四個車輪縱向力（N）；Fyfl、Fyfr、Fyrl和Fyrr分別為四個車輪的側向力（N）；r為整車橫擺角速度（rad/s）；∑Mz為繞z軸慣性矩（N·m）；∑Mztl為車身俯仰力矩（N·m），∑Mzts為車身側傾力矩（N·m）。

根據以上動力學和運動學微分方程，在Matlab/Simulink中搭建7自由度整車動力學模型（如圖2）。

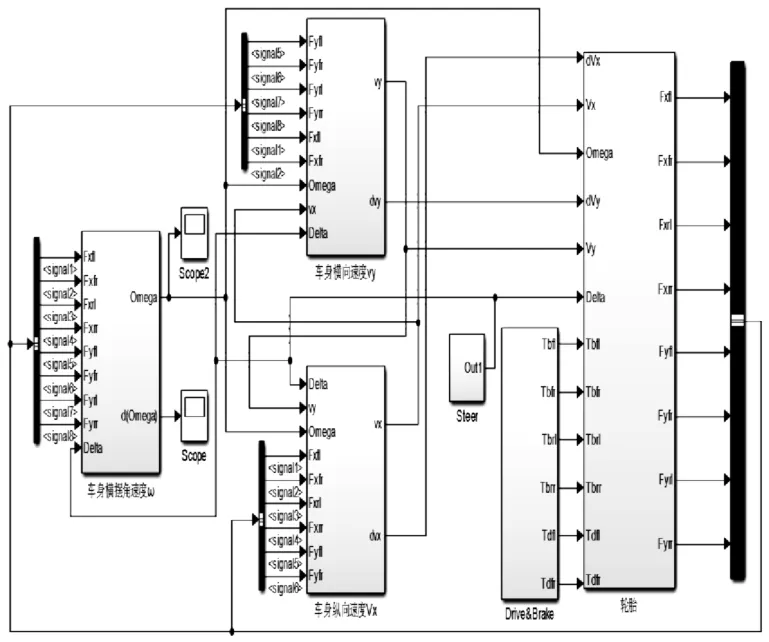
圖2 七自由度整車Simulink動力學模型

1.3 十自由度整車模型DOF_10的建立

懸架變形將引起車身的側傾、俯仰和垂向運動，對汽車的操縱穩定性和行駛平順性。在7自由度整車動力學模型基礎上，通過引入懸架模型和時域路面不平度激勵，建立了10自由度的整車模型DOF_10。

公式（7）、（8）和（9）分別為整車縱向、橫向和垂向動力學微分方程：

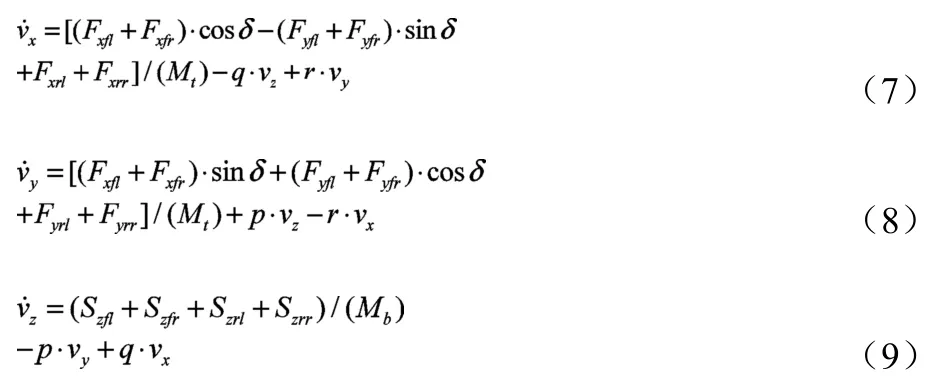
式中：vz為整車的垂向運動（m/s）；p為整車圍繞y軸的轉動角速度（rad/s），q為整車圍繞x軸的轉動角速度（rad/s）；Szfl、Szfr、Szrl、Szrr分別為四個懸架變形產生的力（N）。

公式（10）、（11）和（12）分別為整車側傾、俯仰和橫擺動力學微分方程：

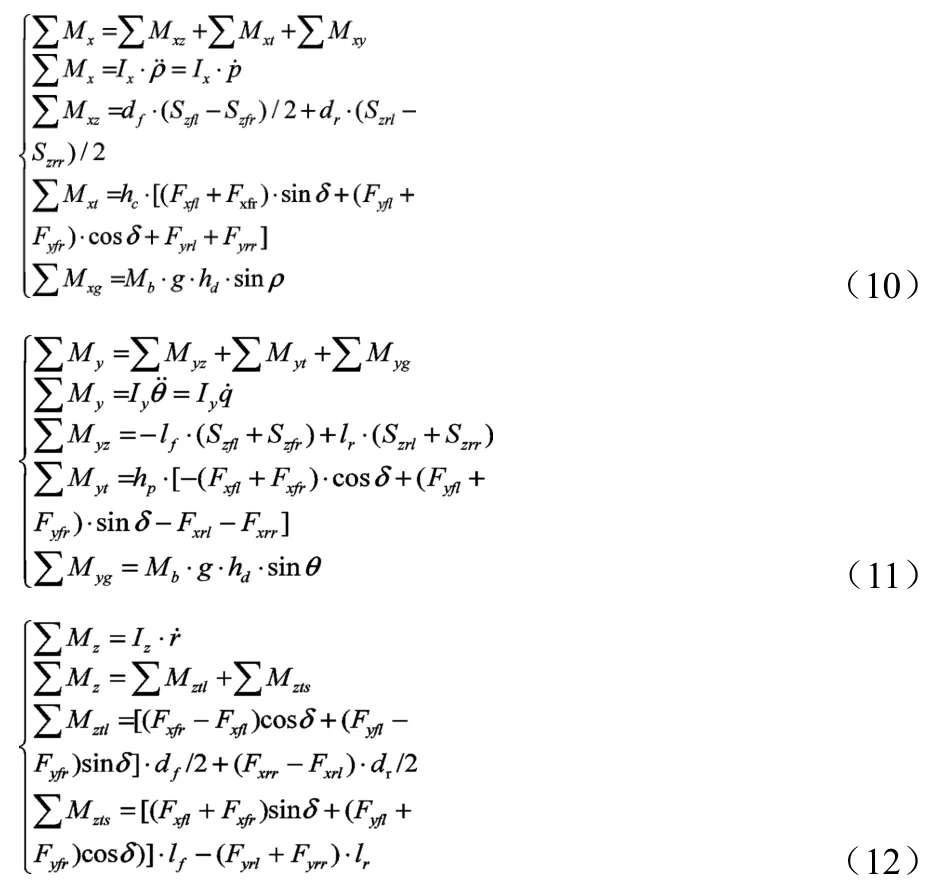
式中：∑Mx、∑My和∑Mz分別為整車圍繞x、y、z軸的慣性矩（N·m）；∑Mxz、∑Mxt和∑Mxg分別為懸架垂向作用力、車輪力和車身重力產生的側傾力矩（N·m）；∑Myz、∑Myt和∑Myg分別為懸架垂向作用力、車輪力和車身重力產生的俯仰力矩（N·m）；∑Mztl和∑Mzts分別為車輪縱向力和側向力產生的車身橫擺力矩（N·m）；ρ和θ分別表示車身的側傾角和俯仰角（rad）；p、q分別表示整車的側傾角速度、俯仰角速度（rad/s）。

圖3 七自由度整車Simulink動力學模型

基于以上公式，在Simulink內建立了10自由度的整車模型（如圖3）。

2 仿真對比分析

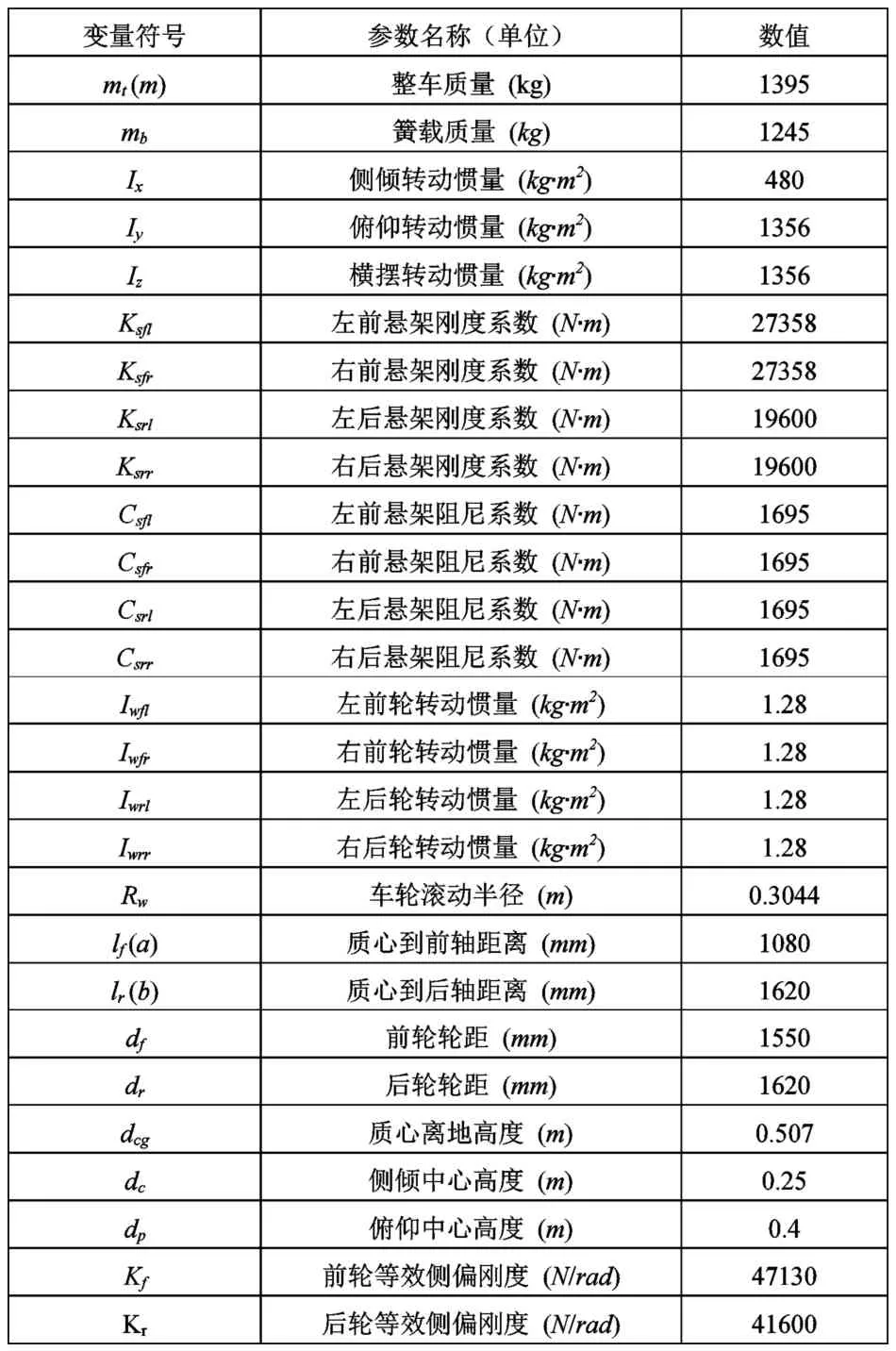
表1 整車參數

仿真工況：在1s時給與方向盤一個正弦信號，模擬整車的單移線工況；改變汽車的行駛車速，通過觀察整車的橫擺角速度變化，分析不同自由度模型的適用工況。相應的輸入信號和仿真輸出曲線如下：

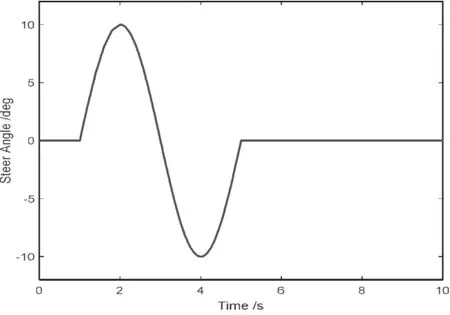
圖4 轉向盤輸入信號

當汽車以 3.6km/h轉向行駛時，DOF_2、DOF_7和DOF_10模型的橫擺角速度變化不大（圖5）；汽車以72km/h轉向行駛時，DOF_2和DOF_7的橫擺角速度曲線基本重合，但DOF_10的橫擺角速度變化明顯較大（圖6）。

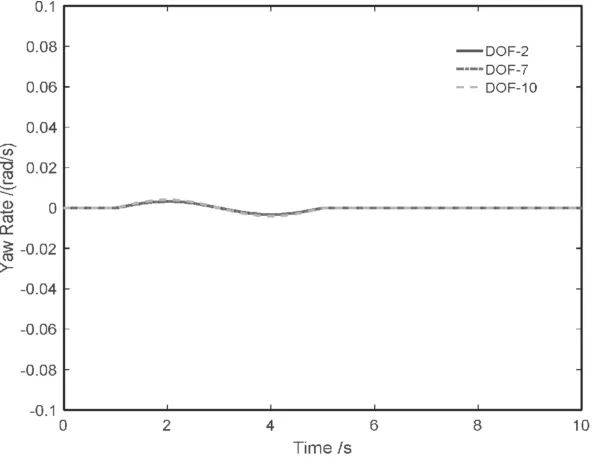
圖5 車速3.6km/h時的仿真輸出信號

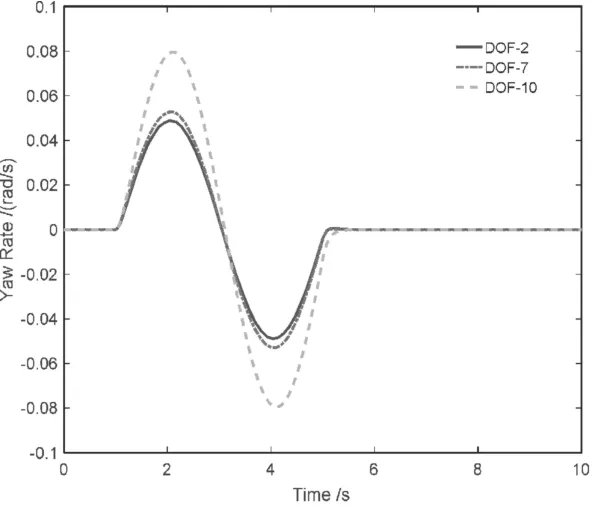
圖6 車速72km/h時的仿真輸出信號

分析以上原因是當汽車以較高車速轉向行駛時，整車的離心加速度顯著增大，進而引起車身側傾；而車身側傾改變了內外側車輪的垂向載荷，從而對輪胎的側偏特性產生影響；最終影響了整車的操穩性，即導致DOF_10模型的橫擺角速度變化顯著。此外，由DOF_2和DOF_7的仿真對比可見，在較小的誤差范圍內，線性二自由度整車模型有關四輪車輛的操穩性仿真結果是準確且高效的。

由以上橫向對比分析可知，本文建立的DOF_10整車模型在傳統動力學模型的基礎上增加了對側傾、俯仰和垂向運動的考慮，不僅較為準確地反映了側傾運動等對整車操穩性的影響，同時可反映車速和路面不平度等對整車平順性的影響，故該模型在“低速-小轉角”、“高速-大轉角”以及“制動滑移”等多種工況的仿真實驗具有顯著的優越性。

3 結論

本文基于Matlab/Simulink分別建立了二自由度、七自由度和十自由度的整車模型，并對所建模型進行了單移線工況的仿真對比實驗。仿真結果表明，十自由度整車模型(DOF_10)可精確地反映整車在“低速-小轉角”、“高速-大轉角”以及“制動滑移”等多種工況下的運行情形，可為多工況下整車控制和自適應巡航等項目的開發提供動力學平臺。