虛擬同步發電機穩定性分析與參數設計

（國網北京市電力公司電力科學研究院，北京 100075）

虛擬同步發電機（virtual synchronous generator，VSG）是一種模擬同步發電機特性的控制策略[1]。VSG可工作在并網或孤島模式，并且能夠像不間斷電源一樣利用下垂特性均分負載[2]。VSG的慣性對電力系統穩定性尤為重要[3]。

VSG控制器的實現目前已有幾種方案，VSG首次由Beck和Hesse在文獻[4]中提出，其實現方案中將傳統發電機的全階模型作為控制系統的一部分。控制中電機模型輸入為所測量的并網點電壓，從而計算出電機電流，然后將這些電流作為電流滯環控制器的參考值來實現發電機特性模擬。文獻[5]和文獻[6]中設計了全階模型的VSG方案，且改為電壓源型設計，更準確地模擬了發電機特性。后續為了降低系統復雜度，將降階模型代替全階模型，不再考慮對同步發電機的電磁暫態模擬，而只是引入了慣性和阻尼[7]。文獻[8]和文獻[9]中的VSG最為簡單，直接采用轉子方程來實現慣性，即由轉子方程和無功功率控制器結合一起為PWM生成模塊提供電壓參考。該設計確保了控制器結構簡單，慣性模擬和無功功率控制確定的電壓參考值可以輸入到電壓電流雙閉環級聯控制器的內部。該控制方案可方便地實現電流和電壓限制，以保護逆變器免受過流影響并避免意外的過調制。盡管使用電壓電流雙閉環級聯控制器可方便地實現逆變器控制，但相對較多的控制器參數和各個環路之間的相互作用使參數整定變難，同時還需詳細分析系統穩定性[10-11]。

對此，先介紹傳統的控制器參數整定。然后，導出VSG線性化狀態空間模型，利用特征值評估小信號穩定性。分析結果表明，如果逆變器以低開關頻率（如2～3 kHz）運行，則內環電流控制器的帶寬受到限制，從而導致系統失穩。因此，提出了一種由線性化模型的特征值的靈敏度矩陣引導的VSG參數調整方法。利用特征值的靈敏度可識別對臨界模態影響最大的參數，同時利用迭代算法將系統特征值從臨界位置移開，從而增強系統穩定性。最后，通過對比仿真驗證了所提出參數整定方法的有效性。

1 VSG控制策略概覽

本文的研究對象為并入電網或者帶負載的三相逆變器，逆變器輸出端包含有LC濾波器。圖1為所分析的逆變器配置示意圖。

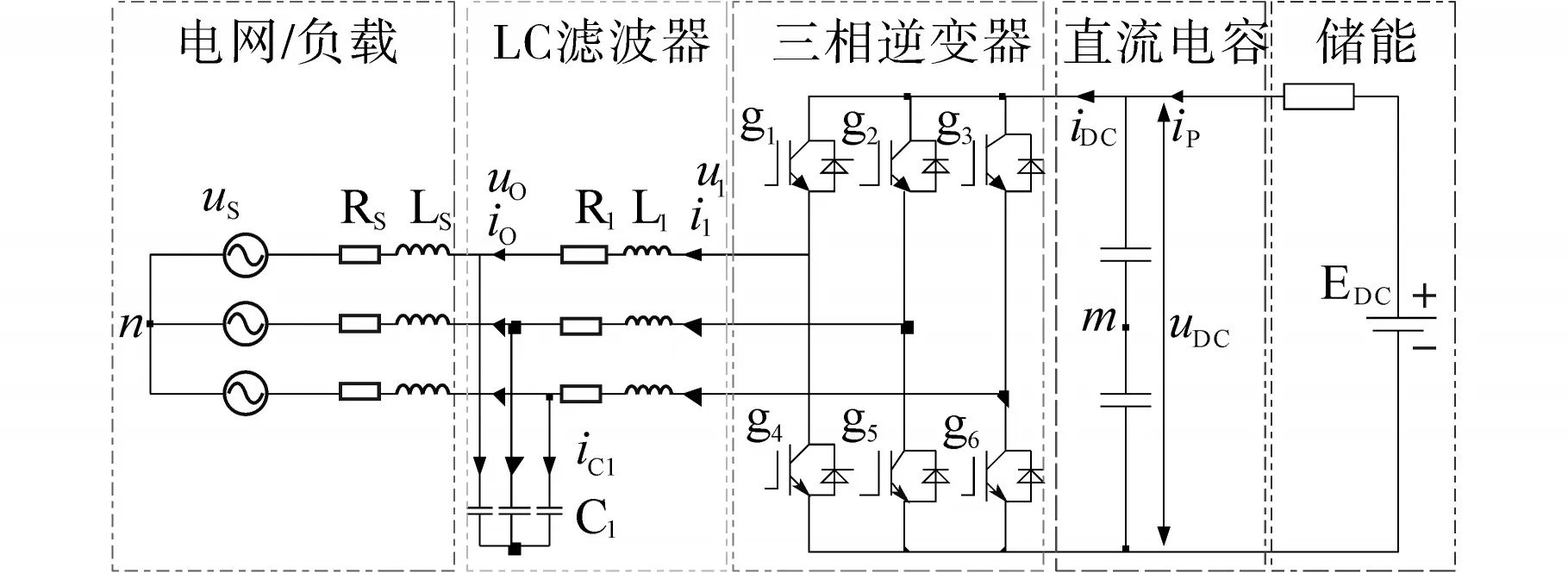
圖1 所分析的逆變器配置示意圖Fig.1 Schematic of the analyzed inverter configuration

本文設計的系統主要參數如下：額定容量Sb=1 MV·A，額定輸出線電壓有效值US_LL_RMS=690 V，LC濾波器電阻R1=0.003（標幺值），LC濾波器電容C1=0.074（標幺值），LC濾波器電感L1=0.08（標幺值），VSG虛擬慣性時間常數Ta=2 s，VSG阻尼系數kd=10 000，額定電網頻率fn=50 Hz，電源電阻Rs=0.003（標幺值），電源電感Ls=0.1（標幺值）。以下分析將以這些參數為基礎。為了簡化分析，假設直流鏈路上的儲能單元所蘊含的能量等效于VSG模擬的電機旋轉慣性。

1.1 同步參考坐標系中的電氣模型

逆變器在忽略開關暫態后可由連續時間平均模型描述：

式中：L1，C1，R1分別為濾波電感、濾波電容和寄生電阻；iLd，iLq分別為電感電流d，q軸分量；uLd，uLq分別為電感前端電壓d，q軸分量；iOd，iOq分別為逆變器輸出電流的d，q軸分量；uOd，uOq分別為逆變器輸出電壓的d，q軸分量；ωb，ωpu分別為頻率基值、標幺值。

逆變器側濾波電感方程如式（1）所示，濾波電容方程由式（2）給出。網側或負載側可由RL電路描述，相應模型形式和式（1）一樣。

1.2 基于VSG的控制系統

圖2為基于VSG的逆變器控制器結構。

圖2 基于VSG的逆變器控制器結構Fig.2 Controller structure of the VSG-based inverter

從圖2中可看出，控制系統含有五部分，其中控制器末端為PWM調制模塊，然后依次是基于同步參考坐標系的電流、電壓控制環，無功功率下垂控制模塊和VSG慣性和阻尼模塊。q軸電壓參考值等于0，同步參考坐標系定向到濾波電感電壓矢量上，d軸電壓參考則是由傳統的無功功率下垂控制器提供的。同步參考坐標系的相位角是根據下式給出的轉子方程對慣性和阻尼模擬后輸出的頻率進行積分得到的。

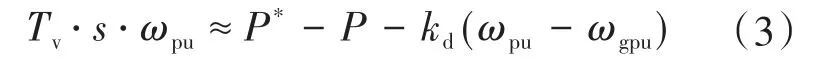
式中：Tv為虛擬轉矩；ωpu，ωgpu分別為角頻率標幺值、電網角頻率標幺值；P*，P分別為有功功率設定值和實際測量值；kd為下垂系數；s為算子。

如果逆變器在并網模式下運行，則VSG通過轉子方程的功率平衡與電網電壓相角同步。因此，VSG的正常運行時不依賴于任何電網同步算法，如鎖相環等。與傳統的發電機一樣，VSG本身也具有孤島運行的能力。

2 傳統的VSG控制器參數整定

2.1 電流閉環參數設計

為了對圖2中所示電流閉環參數進行設計，需考慮逆變器PWM工作模式的延遲效應。采用一階傳遞函數近似PWM的影響，并假設測量電壓的前饋和d，q軸電壓理想解耦，則電流控制器的開環傳遞函數hcc，dq可定義如下：

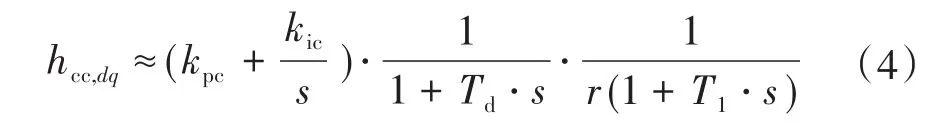
其中

式中：kpc，kic分別為電流閉環PI調節器的比例、積分系數；L1，R1分別為濾波電感、濾波電阻標幺值；l1，r1分別為濾波電感、濾波電阻實際值；T1為濾波電感時間常數；Td為延遲效應近似時間常數；fsw為開關頻率。

基于式（4），按照極點抵消原則來選擇增益，從而產生臨界阻尼閉環傳遞函數，對應kpc和kic的計算式如下：

由式（5）可知，PI參數和帶寬直接受逆變器開關頻率限制。以開環傳遞函數極點抵消原則設置參數得到的系統相角裕度約為65°，可進一步降低相角裕度以獲取更多的控制器增益和帶寬。

2.2 電壓閉環參數設計

從圖2中的級聯控制器結構可看出，電壓閉環參數受到電流控制帶寬的限制。為了簡化，將電流控制器用一階傳遞函數近似。假設d，q軸理想化去耦，則電壓開環傳遞函數為下式：

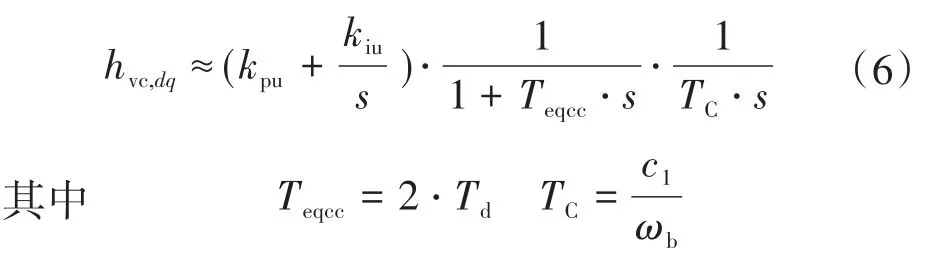
式中：kpu，kiu分別為電壓閉環PI調節器的比例、積分系數；C1，c1分別為濾波電容標幺值、實際值；Teqcc為電流閉環時間常數；TC為濾波電容積分時間常數。

電壓閉環參數是根據確保電壓開環傳遞函數的穿越頻率處最大相角裕度的原則設計的。增加設計參數a將電壓閉環PI調節器的參數整定和閉環傳遞函數阻尼因子ζ關聯，如下所示：

其中

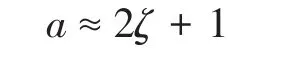
傳統參數整定要求電壓環和電流環間帶寬保持較大差異。這是通過增大a的值來保證的，直到電壓閉環帶寬比電流控制帶寬低至少十倍。

3 穩定性和參數敏感度分析

對于圖2中所示的VSG控制方案，必須顯著降低電壓控制閉環的帶寬，否則無法確保無功功率控制和虛擬慣性控制的預期性能以及整個控制系統的穩定性。而如果電流控制閉環帶寬較低，則可能發生不同控制回路之間的相互作用。故下面對控制系統穩定性和動態性能開展分析。

3.1 狀態空間系統模型

由圖1和圖2，可導出VSG小信號數學模型如下式所示：

其中

式中：“Δ”代表狀態變量在工作點附近的小信號擾動；kFFu為電流閉環中電壓反饋系數；kFFi為電壓閉環中電流反饋系數；ξ，σ分別為電流和電壓控制器中積分器的狀態輔助變量。下標“0”為工作點的變量值；γ為逆變器控制系統和電源相關的兩個同步坐標系之間的相位差，有γ0=θVSG，0-ωgt0。

3.2 特征值分析和系統穩定性

基于式（8）中狀態矩陣的特征值可分析VSG穩定性。

圖3為調節a從0.5變化至50時，系統特征值在復平面中的軌跡。圖3為前述傳統參數整定的3種情況，但具有不同的開關頻率。當系統不穩定時，特征值為黑色，圖3中結果表明，當開關頻率為2 kHz時，系統穩定工作范圍非常窄，當開關頻率增加到5 kHz時，系統穩定區間更寬，但仍對控制閉環的參數整定非常敏感。進一步將開關頻率提高到10 kHz，系統具有相當寬的穩定工作范圍，這意味著傳統參數整定方法適用于高開關頻率的低功率逆變器設計，如kW級小規模微電網應用VSG技術時。

圖3 對應參數a變化的系統特性值軌跡Fig.3 The trajectories of the system eigenvalues with variation of parameter a

圖3所示的特征值軌跡分析結果表明，系統穩定性受電流閉環帶寬的強烈影響，即受到逆變器開關頻率影響。此外，當VSG方案中采用相對較低的開關頻率時，傳統的參數整定方法可導致較差的動態響應性和低穩定裕度，因為各個級聯控制閉環不能充分解耦。實際上，盡管各個控制閉環設計均為穩定的，但它們之間的相互作用會對系統整體穩定性產生負面影響，從而導致穩定工作范圍變窄。因此，有必要探索新的參數整定方法。

3.3 參數靈敏度矩陣

定義系統極點的參數靈敏度為系統特征值對于系統參數的導數，從而可通過參數靈敏度辨識對系統臨界特征值影響最大的參數，并可以揭示修改這些參數影響特征值位置的規律。

假設n階系統具有k個可調參數，靈敏度矩陣為n×k階。參數ρk相對于特征值λn的靈敏度αn，k可由下式表示：

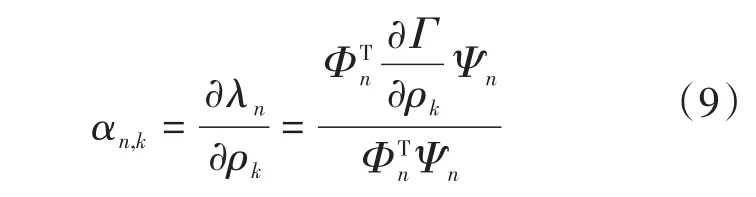
式中：Ψn，ΦnT分別為與特征值λn相關聯的左、右特征向量；Г為n階系統的狀態矩陣。靈敏度的實部和虛部分別與沿著實軸、虛軸的極點位置的導數相關聯。由于極點位置的實部表征了系統的穩定性，故下面僅需研究靈敏度矩陣的實部。

參數靈敏度的兩個例子如圖4所示，系統配置見第1節中系統主要參數設置，開關頻率為2 kHz，設定參數a=4。

圖4 參數敏感度分析Fig.4 Parameter sensitivity analysis

圖4a為參數整定導致系統失穩的情況下不穩定特征值的分布，其中深色點代表穩定特征根，淺色點代表不穩定特征根。圖4b為不穩定的特征值對13個參數的靈敏度，該不穩定的特征值位置主要取決于控制器參數kpc和kpu，但LC濾波器參數和電網電感參數也有一定影響，如kpc或kpu增大，則該特征值將向左移動，從而穩定了系統。類似地，圖4c、圖4d繪出了接近于虛軸的另一個特征值的分析結果，圖4c中淺色點代表接近于虛軸的特征值，反之則為深色點。在這種情況下，電網電感參數有顯著影響，但特征值也受kiu和kd的影響。

4 VSG控制器參數整定算法

利用3.3節的靈敏度矩陣可整定系統參數。下面將引入VSG控制器的新型參數整定算法。參數整定基于一個迭代過程，其中每一步都將修改控制器參數將系統極點配置到一個更合適的位置。

圖5為參數整定算法流程圖。

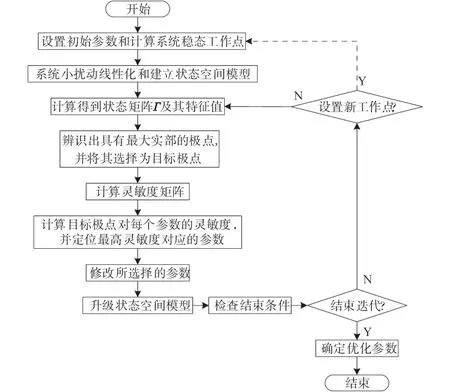
圖5 參數整定算法流程圖Fig.5 Flow chart of parameter tuning algorithm

由圖5可知，VSG控制器的新型參數整定算法主要步驟如下：首先，將系統參數和一組初始控制器參數配置作為迭代起點，初始參數通常是采用傳統整定方法得到的。然后，計算出穩態工作點。值得注意的是，計算得到的工作點可能不穩定，但是不會影響到后續迭代過程和最終結果。接著，計算圍繞該工作點的小擾動線性化系統的狀態矩陣Г及其特征值。同時，辨識出具有最大實部的極點并將其選擇為當前優化步驟的目標。繼續計算靈敏度矩陣以得到該關鍵極點相對于每個可調參數的靈敏度，并找到最高靈敏度對應的參數，在每次迭代中，略微改變該參數。靈敏度的符號確定了參數是增加還是減小，以便迫使目標極點向左移動。

通常，可以根據預設的終止條件終止迭代過程。為簡單起見，在該示例中，迭代過程采用固定數量的迭代。示例中整定后的參數將確保最關鍵的極點移動到具有較小實部的位置。盡管可以考慮更高級的改變系統參數的標準，但該算法采用簡單條件通常是有益的，因為造成不穩定的極點將逐漸移動到穩定區，而極點特性將通過迫使特征值向左移動而得到改善。然而，值得注意的是，某些參數的修改可能導致其他極點右移，導致算法可能表現出在每個迭代周期的不同臨界極點之間不停交替振蕩。還要注意的是，可調參數不僅僅限于控制器增益，還包括物理參數如濾波電感和濾波電阻等。從這個角度來看，所提出的算法還可用于系統設計早期階段。

5 仿真驗證

圖6 參數整定過程Fig.6 Parameter tuning process

對圖1、圖2所示的逆變器及其VSG控制器進行了基于迭代算法的參數整定，并將參數設置后的系統性能與傳統參數設計進行對比，從而驗證新型算法的效果。其中可調參數集設為7個參數，即kpc，kpu，kic，kiu，ωf，pu，mq和kd，因為考慮主回路參數已固定。圖6a、圖6b為隨著迭代過程參數改變導致的系統極點位置變化，從圖中可以看出，由于極點向左偏移，系統動態響應更快，同時穩定裕度更大。圖6c、圖6d給出了迭代運算中參數kpc和kpu具體的優化過程。由圖6中可看出，電流閉環控制器的增益kpc在前約1 500次迭代中保持不變，但電壓閉環控制器的增益kpu增加，隨后kpu在約2 500次迭代中保持不變，而kpc持續增加。

選擇2 500次迭代后得到的參數集合作為最終結果，以避免過高的電流控制器增益。將這些參數在系統中設定后與傳統參數整定（a=3）得到的系統性能進行時域仿真對比，工作點選擇一致，然后比對功率參考階躍后的系統動態響應。圖7、圖8分別為使用傳統參數整定方法和新型參數整定方法得到系統動態響應結果，其中Δ|uO|為輸出電壓動態擾動值，Δ|iO|為輸出電流動態擾動值，Δωpu為VSG轉速動態擾動值。對比圖7、圖8可看出，系統穩態輸出是一致的，兩種時域仿真都產生了穩定的系統動態和足夠的阻尼振蕩，但是，圖8的動態響應速度明顯更快。同時，如前所述，傳統參數整定方案得到系統穩定區較小，故對干擾、參數不匹配、工作點變化更為敏感。而利用所提出的算法獲得的參數集可得到更穩定的系統運行條件。

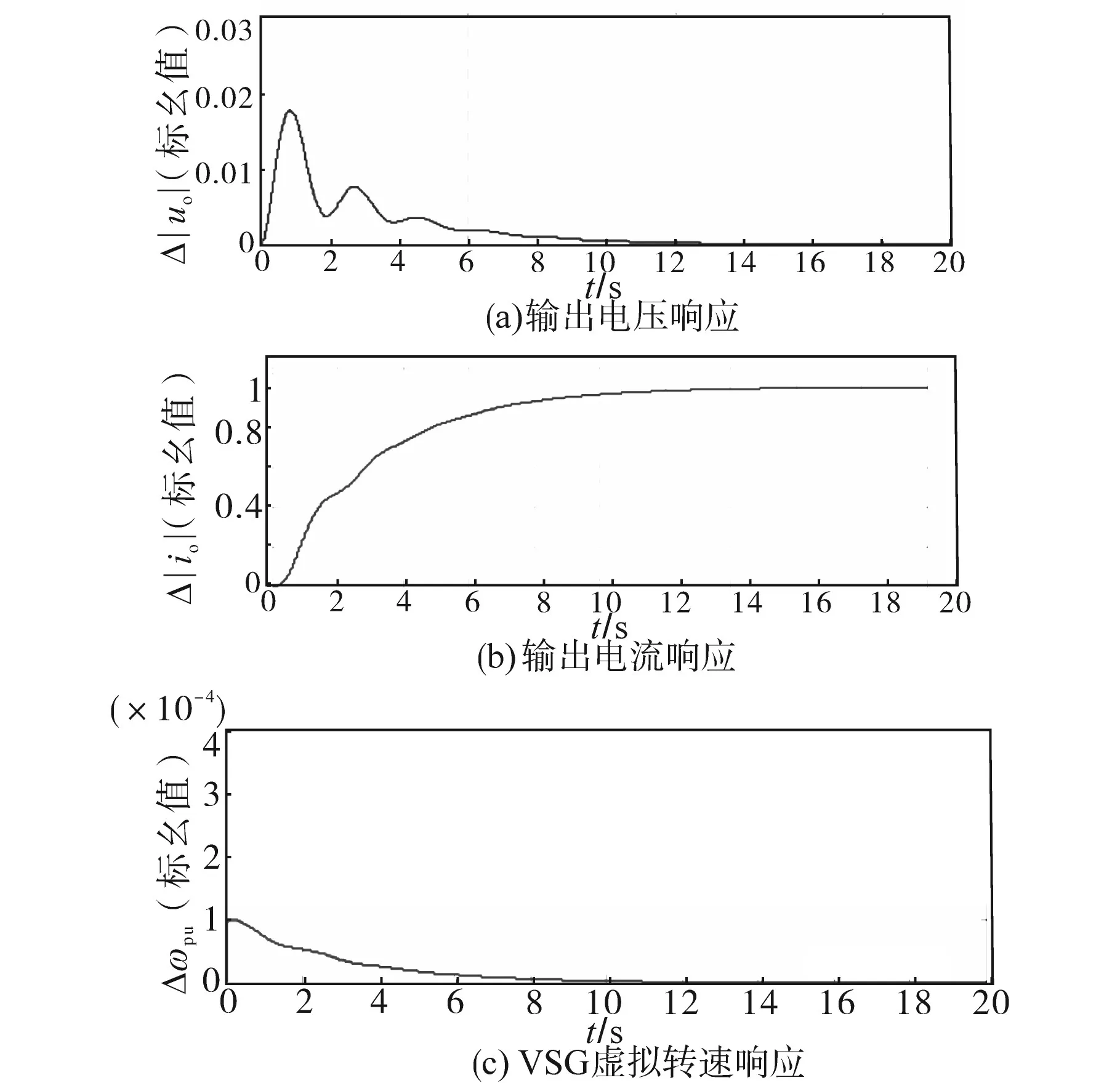
圖7 與傳統參數整定相對應的時域仿真結果Fig.7 Time domain simulation results corresponding to traditional parameter tuning

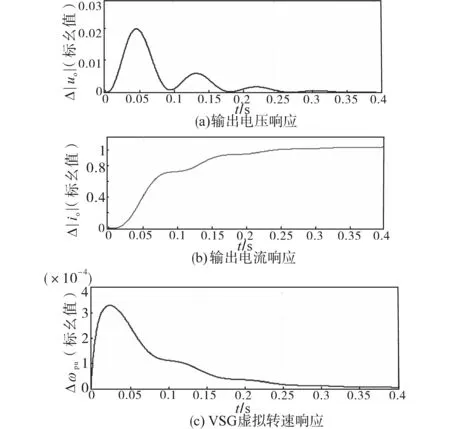
圖8 與新型參數整定相對應的時域仿真結果Fig.8 Time domain simulation results corresponding to new parameter tuning

6 結論

圍繞三層級聯閉環結構的VSG控制器參數設計及其穩定性問題，設計了一種基于特征值靈敏度矩陣引導的參數優化整定迭代算法，現總結結論如下：

1）基于功率外環、電壓和電流控制閉環構建的VSG控制器具有易于設置保護的優點，但存在參數設置復雜的問題；

2）在分析傳統參數整定方案弊端的基礎上，設計了一種由線性化系統模型特征值靈敏度矩陣引導的VSG參數整定方案，新方案在傳統整定參數基礎上經由多次迭代優化后可獲取確保系統穩定的優化參數；

3）時域仿真對比計算證明了基于參數靈敏度的迭代方法比傳統方法更有效，可顯著地改善VSG動態性能。