各向異性永磁同步電機低速控制策略

趙慧峰 ，劉琳

（1.三門峽職業技術學院智能制造學院，河南 三門峽 472000；2.河南科技大學應用工程學院，河南 三門峽 472000）

永磁同步電機（permanent magnet synchronous motor，PMSM）由于其效率高、動態響應快和功率密度高在各種工業領域中得到了廣泛的應用[1-3]。而PMSM的無速度傳感器技術成為了近年來的一個研究重點，因為其不需要機械傳感器，可顯著降低成本和提高可靠性。同時，隨著PMSM應用范圍趨于廣泛，PMSM拓撲結構得到了創新，如轉子各項異性乃至純同步磁阻電機等[4]的誕生。適當增加各向異性后使得PMSM在無速度傳感器控制上更具有優勢，包括高速（延伸至弱磁區）和低速運行工況。

對于PMSM的無速度傳感器控制技術，目前已經有較多文獻進行了報道[5-18]，具體可按照電機運行轉速分類[5]。對于低速運行，即電機轉速低于額定轉速的20%時，可將高頻電流疊加在基頻電流上注入，利用轉子各向異性觀測轉子位置[6-8]。在更高的速度下，可以使用基于基頻信號的觀測器實現轉子位置觀測，如反電動勢（backelectromotive force，BEMF）觀測器或磁鏈觀測器[9-10]。文獻[11]、文獻[12]同時使用了高頻注入和觀測器這兩種技術，即合并兩種技術，但僅在過渡區能共同工作。然而，持續的高頻注入對PMSM驅動性能不利，因為其將導致轉矩脈動，并產生額外的噪聲和振動。值得注意的是，有一些應用場合不需要在整個轉速范圍內閉環調節，首先可以用開環方式啟動，然后在適當轉速時進行閉環控制，這樣可以消除高頻注入問題[13]。文獻[14]采用自適應集總電動勢模型預測控制得到電機初始位置，這雖然解決了電機啟動問題，但穩態閉環調節最小轉速仍與基于BEMF的無速度傳感器控制方案的性能相關。通常，電壓測量的信噪比將使得基于BEMF的轉速估計在低速時失效。文獻[15]通過滑模觀測器擴展了運行轉速范圍，但對控制參數強依賴。文獻[16]中研究了逆變器非線性引起的諧波與可控轉速下限之間的關系，結論為低速時觀測器帶寬的減小可改善抗干擾能力，使調速范圍擴大。而文獻[17]對逆變器中的電壓誤差進行適當補償，也可擴大轉速調節范圍，但補償算法需要進行精細的參數整定才能具有較好的效果。文獻[18]指出當轉矩和轉速具有不同的符號時，即電機在發電模式下將出現不穩定，故在高頻注入和BEMF估計之間給出了選擇過渡區，可避免發散，代價是延長了高頻注入信號的使用時間。

基于上述文獻研究，本文設計了一種新型的PMSM低速控制方案。新型控制策略是基于改進的BEMF觀測器來實現的，避免了傳統觀測器可能出現的不穩定，從而使轉速調節范圍向下擴展，且無需注入高頻信號。最后，進行了新方案的實驗驗證。

1 BEMF觀測器分析

PMSM的數學模型可用電壓方程描述如下：

其中

式中：ud，uq分別為定子電壓d，q軸分量；id和iq為定子電流d，q軸分量；Ld和Lq為d，q軸定子電感；R為定子電阻；Ψmg為永磁磁鏈；ωme為轉子電角速度；p為極對數；ωm為轉子機械角速度；edq為BEMF矢量；J為常值矩陣。

值得注意的是，由于PMSM通常具有磁飽和特性，故電感取決于id和iq，故式（1）中的電感矩陣必須考慮定子電流影響。無速度傳感器控制中需估計轉子位置θme。由于矢量edq與轉子軸方向正交，因此可以由BEMF觀測器來間接估計轉子位置。根據觀測器估計的轉子位置定向dq坐標系，可得：

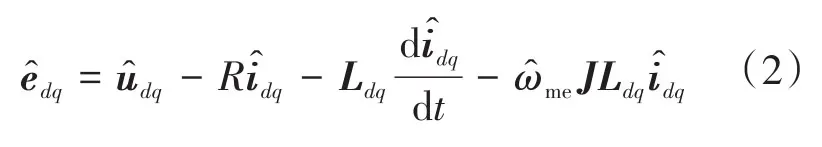
其中：上標“^”為對應變量的估計值。

式中：δ為轉子位置估計誤差。

聯立式（2）和式（4）可得：

其中

式中：Id，Iq為工作點電流d，q軸分量；Ωme為工作點轉速。

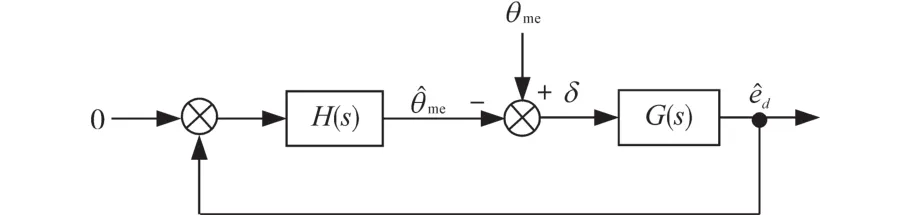
圖1 位置估計框圖Fig.1 Block diagram of the position estimation

在圖1中，如果設ωme為常數，則可以將轉子位置θme視為斜坡變化的擾動。根據自動控制原理，H（s）需包含要抑制的擾動模型，即采用雙積分器才能達到控制目標。控制器還要滿足將調節為零的要求，此外，為了使控制器的設計獨立于工作點，設計H（s）為

式中：kp和ki分別為PI調節器的比例和積分系數；s為拉普拉斯算子；kwp為取決于工作點的增益；LΔ為d，q軸電感差值。

可利用估計量進行計算如下：

圖1中，H（s）為PI調節器和純積分調節器的級聯。式（6）中的分子是一個超前補償器，為了整個反饋閉環的穩定，必須在選定的增益對應穿越頻率點上產生令人滿意的相角裕度。式（6）中出現的零點可以是最小相位零點或非最小相位零點，取決于Iq和Ωme的符號。當Iq和Ωme的符號相同時，電機處于電動機模式，式（6）中出現的零點具有最小相位，否則為非最小相位零點，對應為電機工作在制動模式。

對于式（6）中出現的零點是最小相位零點，則單零點補償器足以穩定整個閉環。若式（6）中出現的零點是非最小相位零點，則使用單零點補償器達不到預期效果，故需要引入額外的相位超前來補償非最小相位零點在高頻下引入的相位滯后。可以限制最大控制帶寬來保證PMSM在任何運行條件下都穩定，然而這樣的設計過于保守。

另一種方案是在觀測器的工作區域上設置邊界，這需要分析觀測器的穩定性限制，即d，q軸電流的極限。

圖1所示閉環系統的極點即對應特征方程的根，特征方程為傳遞函數的分子，特征方程及其根如下所示：

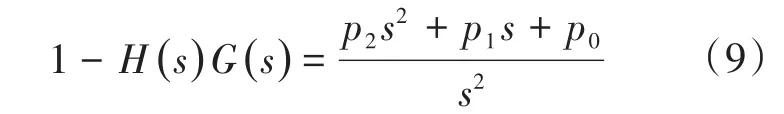
其中

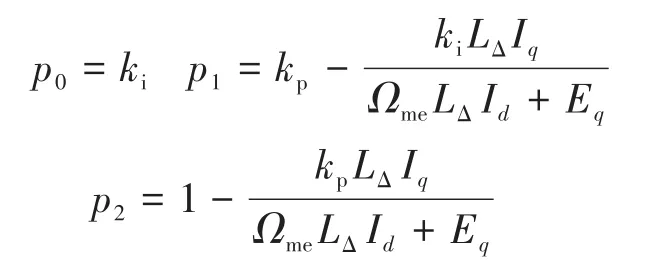
式中：p0，p1和p2為特征方程的系數；H（s）G（s）為開環傳遞函數。

要滿足反饋系統穩定，閉環極點必須具有負實部，根據經典控制理論，只要p0，p1和p2的符號相同，則可以保證穩定性。那么根據轉速和電流的符號，可進行分類討論如下。

首先，假設ωme＞0（對于ωme＜0，結論是類似的）。其次，假設Id≤0，這通常發生在磁場定向控制電機以最大轉矩電流比（maximum torque per ampere，MTPA）運行時[19]。由于LΔ＜0，因此式（9）中的系數符號由Iq的值確定如下：

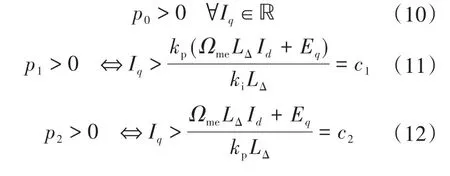
式中：c1和c2為判據值。

因此，如果滿足下式，觀測器是穩定的。

根據先前引入的假設，即Ωme＞0，Id≤0和LΔ＜0，則c1和c2總為負，這可以得出結論，觀測器僅在Iq為負的情況下可能變得不穩定。式（11）的條件取決于轉速、控制器參數、永磁磁鏈、各向異性LΔ及d軸電流Id。永磁磁鏈定義為正，只要Lq＞Ld，各向異性LΔ即為負。將LΔ乘以負的d軸電流將添加一個正項到Ψmg，這減小了由c1設定的下限。換句話說，負的d軸電流增加了觀測器的穩定工作區域。另一方面，穩定區域在很大程度上取決于控制器參數，這需要增加設計約束。

2 改進型BEMF觀測器

基于前述分析，設計改進BEMF觀測器以解決不穩定性問題。導致觀測器不穩定的原因是式（6）中存在非最小相位零點，故修改BEMF觀測器的方程如下：

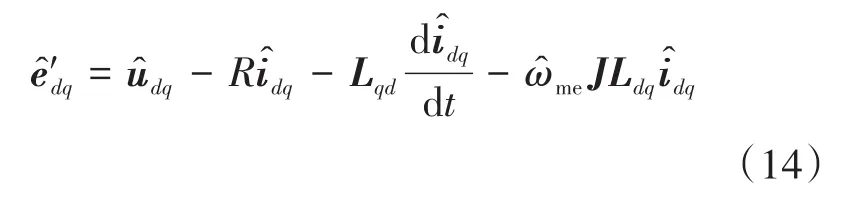
其中

式中：Lqd為新的電感矩陣。

對比傳統觀測器式（2）和改進觀測器式（14）可得以下關系：

對式（16）進行小擾動線性化處理可得到：

這清楚地表明了如何通過施加零e?'d分量來使位置估計誤差δ為零。使用改進觀測器后，由式（6）描述的給定工作點附近的傳遞函數G（s）變為

式（18）中沒有零點，因此可以任意選擇控制帶寬和相角裕度，閉環系統均是穩定的。H()s保持與之前式（7）相同，式（7）期望的增益對應穿越頻率ωc處特定的相角裕度φm由下式得到：

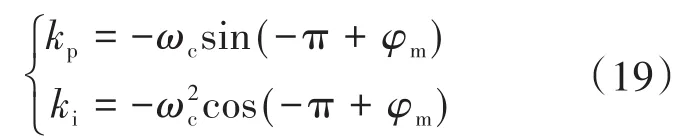
新的BEMF觀測器可保證在任何工況下系統的穩定。對于BEMF信號中的高次諧波，可通過相位超前補償器處理，使得在高頻下具有較好的噪聲抑制能力。式（7）可由下式代替：

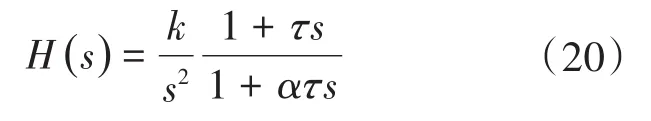
式中：k，τ和α為設計參數，同時必須滿足以下條件：k＞0，τ＞0和0＜α＜1。

合理設置補償器參數后可使控制器具有所需的帶寬和相角裕度，具體為

圖2為改進型BEMF觀測器原理圖，圖中可看出其基于式（14）由D變換后的和，以及估計出反電動勢，然后經過相位超前補償器H（s）處理后可獲取較為準確的位置角。

圖2 改進型BEMF觀測器原理圖Fig.2 Schematic of the improved BEMF observer

圖3為傳統BEMF觀測器和改進型BEMF觀測器的伯德圖對比圖。由圖3可知，相位超前補償器H（s）在高頻段的衰減更大。

圖3 H（s）G（s）伯德圖對比Fig.3 Bode diagram comparison of the H（s）G（s）

3 實驗驗證

為了驗證所設計的各向異性PMSM低速控制策略，構建了PMSM驅動實驗平臺，開展了相關實驗。圖4為測試平臺示意圖。圖4中，設置了一個轉子位置反饋選擇開關SW，當SW=1時選擇測量得到的轉子位置，而當SW=0時，采用估計的轉子位置作為反饋。增加選擇開關是為了配合后續的不同測試。基于兩臺PMSM開展實驗，參數如表1所示。

圖4 測試平臺示意圖Fig.4 The schematic of the test platform

表1 電機參數Tab.1 Parameters of the motors

3.1 1#PMSM測試結果

通過在圖2中設置e?d階躍變化可測試所提出的改進型BEMF和傳統BEMF觀測器的動態響應。在測試期間，設置SW=1，因為測試目標是評估觀測器性能。電機處于轉速控制模式，同時拖動轉矩為-0.25TN，使其在制動模式下工作。圖5為e?d階躍變化測試結果。由圖5可知，傳統BEMF觀測器具有明顯向下的超調，這是非最小相位零點導致的，但改進型BEMF觀測器消除了該超調，性能增強。

圖5 e?d階躍變化測試結果Fig.5 Test results of the e?dstep change

在許多應用中，控制各向異性較小的PMSM時，往往忽略磁阻轉矩分量并設置id=0而非采用更復雜的MTPA控制。在這種情況下，使用傳統觀測器需更加注意，因為各向異性可能導致不穩定。下面采用1#PMSM進行測試，因為其具有更低的各向異性。圖6為拖動轉矩增加時，采用改進型BEMF和傳統BEMF觀測器的對比測試結果，其中曲線A為改進型BEMF方案，曲線B為傳統BEMF方案。

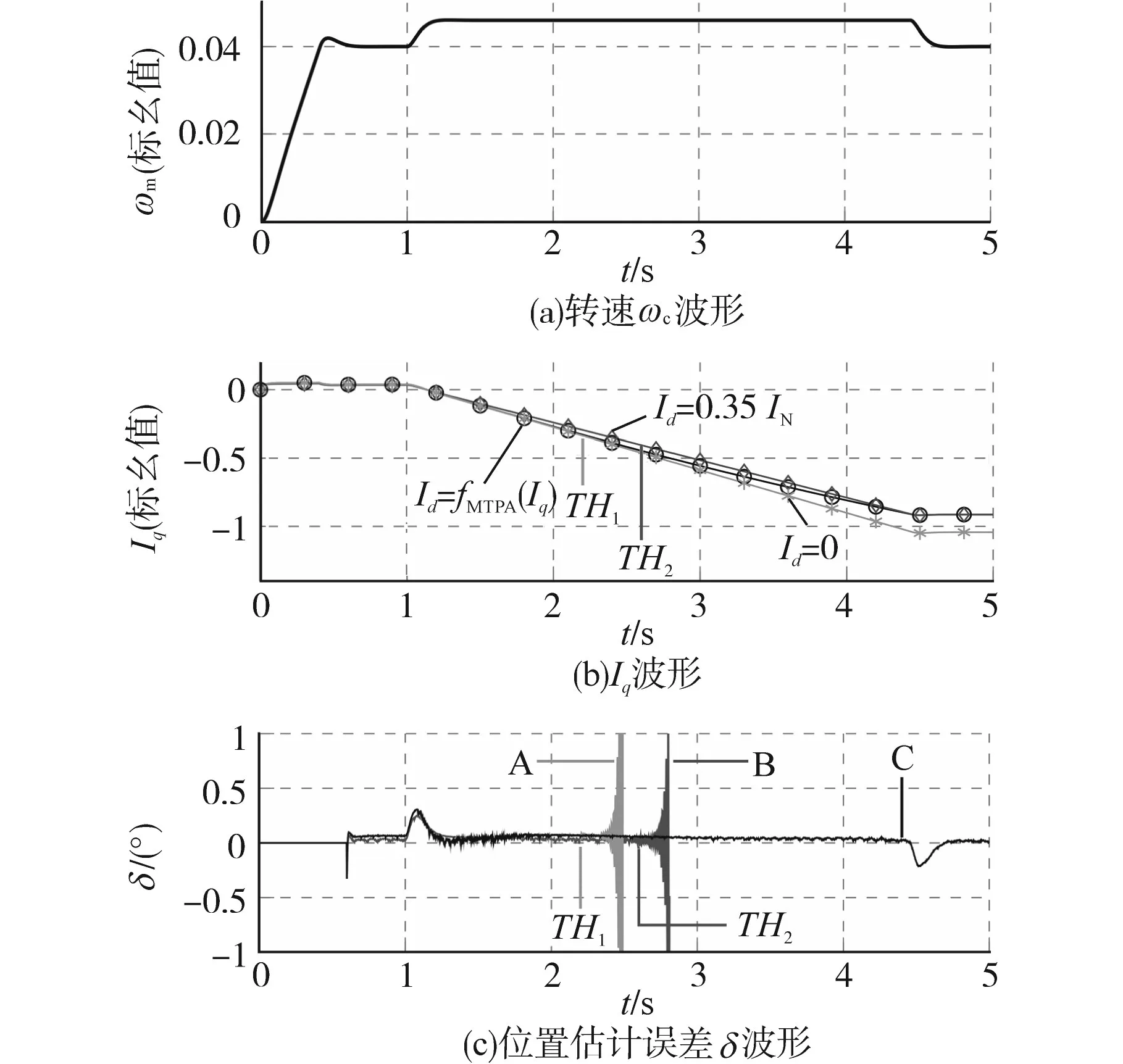
圖6 拖動轉矩增加時的測試結果Fig.6 Test results at increasing dragging torque

測試中設置SW=1以保持系統穩定，同時采用觀測器獲取，但不用于反饋。調整H（s）的參數使得ωc=80π（rad/s）和φm=80°。電機以低速（0.04ωN）運行，并且在t=1 s時增加拖動轉矩。圖6c中曲線A（改進型BEMF方案）對應工作點Id=0，在這種情況下，根據式（13）的計算為Iq＞-0.346IN，標記在圖6b中為TH1，測試結果表明采用傳統觀測器時，位置估計誤差δ在Iq達到閾值TH1之后即發散。圖6c中曲線B（傳統BEMF方案）對應工作點Id=-0.32IN，這是MTPA控制時對應額定負載下施加的電流。根據式（14）可計算得到Iq＞-0.4IN，標記在圖6b中為TH2，同樣，測試結果表明采用傳統觀測器時，位置估計誤差δ在Iq達到閾值TH2之后即發散。圖6c中曲線C為采用改進型BEMF觀測器的測試結果，設置Id=0，因為此時為最惡劣的運行條件，測試結果表明系統一直保持穩定直至Iq的改變結束。

圖7、圖8為設置SW=0時，使用估計轉子位置時的PMSM低速驅動控制測試結果，其中曲線A為改進型BEMF方案，曲線B為傳統BEMF方案。

圖7 轉矩固定轉速斜波下降的測試結果Fig.7 Test results with torque fixed and speed ramp drop

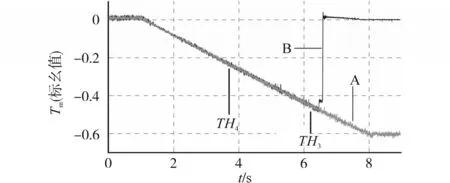
圖8 轉速固定轉矩斜波增加的測試結果Fig.8 Test results with speed fixed and torque ramp increase

圖7為恒定負載轉矩0.5TN，設置斜坡減速的轉速波形。由于式（13）計算得到的不穩定閾值和轉速相關，故存在使傳統觀測器變得不穩定的最小轉速，即TH3=0.078ωN，測試結果顯示當轉速達到TH3后，系統發散。在同樣的測試條件下，采用改進型的BEMF觀測器可以使系統在0.015ωN以上范圍內保持穩定控制。

圖8為保持轉速恒定為0.04ωN，設置負載轉矩從0增加至0.6TN的測試波形。由前述推導采用傳統觀測器對應的轉矩閾值TH4=-0.25TN，實驗結果顯示實際閾值約為TH5=-0.48TN，這是因為電機的磁飽和降低了實際閾值，當運行轉矩超過閾值后，系統發散。在同樣的測試條件下，采用改進型的BEMF觀測器可以使系統保持控制穩定。

3.2 2#PMSM測試結果

相對于1#PMSM，2#PMSM的各項異性更為明顯，如表1所示。同時，電機諧波含量更高，考慮到BEMF觀測器僅基于基頻，諧波可能會對系統造成不利影響，故前述設計的相位超前補償器是一種較好的對策。

圖9為電機空載時轉速從0.15ωN降至0.1ωN的測試結果，其中曲線A為測量轉速曲線，曲線B為改進型BEMF方案得到轉速曲線，曲線C為傳統BEMF方案得到轉速曲線。

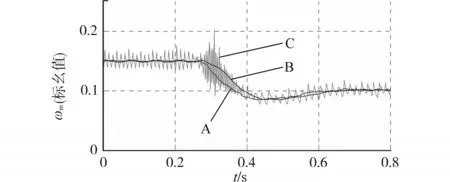
圖9 空載轉速下降測試結果Fig.9 Test results of speed drop with no load

圖9中，兩種觀測器的參數都調整至ωc=20π（rad/s）和φm=80°。出于安全考慮，設置SW=1。由于電機空載運行，故電壓測量的信噪比非常低，對BEMF觀測器來說是非常嚴酷的條件，從測試結果來看，相對于傳統觀測器設計，采用相位超前補償器產生了更平滑的轉速信號。

圖10 固定負載轉矩轉速下降測試結果Fig.10 Test results with speed drop and fixed load torque

圖10為電機拖動轉矩為-0.15TN固定負載轉矩時的轉速從0.15ωN降至0.1ωN的測試結果，其中曲線A為測量轉速曲線，曲線B為改進型BEMF方案得到轉速曲線，曲線C為傳統BEMF方案得到轉速曲線。由圖10可知，改進型BEMF觀測器沒有出現任何不穩定并保持了較好的轉速估計精度。而傳統觀測器在電機低速時產生了明顯的振蕩。進一步，設置SW=0進行閉環測試，結果如圖11所示。考慮到零轉速時，基于BEMF的觀測器不能單獨工作，故首先設置SW=1啟動2#PMSM后在t=1.25 s再改變SW=0激活觀測器。測試時轉速控制為0.2ωN，突加0.5TN的負載轉矩。測試結果顯示采用相位超前補償器后，在突加負載后，改進型BEMF觀測器也表現出平穩的運行，即圖11a所示突加負載擾動后轉速保持了觀測值較為恒定。

圖11 無速度傳感器閉環控制測試結果Fig.11 Test results of speed sensorless closed-loop control

4 結論

圍繞各向異性PMSM的無速度傳感器控制策略在低速區的擴展，本文設計了一種基于改進BEMF觀測器的新方案，總結全文為：

1）傳統BEMF觀測器由于存在非最小相位零點，在電機低速時可能導致系統不穩定，而改進型BEMF觀測器通過引入新的變換，以及相位超前補償器改善了控制結構，從而增強了系統穩定性；

2）對比實驗結果顯示，相對于傳統BEMF觀測器方案，改進型BEMF觀測器能顯著改善PMSM低速區運行特性，同時相位超前補償器對各向異性產生的諧波具有明顯的抑制作用，控制性能優良；

3）進一步的研究方向為：分析故障發生后的系統特性，設計有容錯能力的觀測器。