基于一題多解的數(shù)學(xué)建模教學(xué)
——以人教版第十一冊第六單元“濃度問題”為例

（廈門大學(xué)附屬實(shí)驗(yàn)小學(xué)，福建 漳州 363123）

數(shù)學(xué)模型一般是指對特定的問題用數(shù)學(xué)語言、符號或圖形等形式來刻畫、描述、反映的數(shù)學(xué)結(jié)構(gòu)。數(shù)學(xué)模型有效地反映了思維的過程，是將思維過程用語言符號外化的結(jié)果，學(xué)生對數(shù)學(xué)模型的理解、把握與建構(gòu)的能力，在很大程度上反映了其數(shù)學(xué)思維能力及數(shù)學(xué)觀念。一題多解是在解決一道題時，從不同思維角度、方法和知識模塊入手，通過解題過程，讓學(xué)生體會不同知識點(diǎn)的交匯和融會貫通，從本質(zhì)上看是把數(shù)學(xué)模塊系統(tǒng)化、連貫化、整體化。教師要引導(dǎo)學(xué)生多角度思考、解決問題，滲透模型思想，訓(xùn)練模型思維，讓學(xué)生在觸類旁通的過程中建立不同的解題模型。

一、尋求等量關(guān)系，建立解題模型

《義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)（2011 年版）》指出：“模型思想的建立，是學(xué)生體會和理解數(shù)學(xué)與外部世界聯(lián)系的基本途徑，建立和求解模型的過程包括：從現(xiàn)實(shí)生活或具體情境中抽象出數(shù)學(xué)問題，用數(shù)學(xué)符號建立方程、不等式、函數(shù)等表示數(shù)學(xué)問題中的數(shù)量關(guān)系和變化規(guī)律，求出結(jié)果，并討論結(jié)果的意義。這些內(nèi)容的學(xué)習(xí)有助于學(xué)生初步形成模型思想，提高學(xué)習(xí)數(shù)學(xué)的興趣和應(yīng)用意識。”數(shù)學(xué)模型思想所體現(xiàn)的過程，就是在具體情境中，抽象出數(shù)學(xué)問題，分析和解決問題的過程。［1］教學(xué)中，要針對具體問題，聯(lián)系生活實(shí)際，進(jìn)行必要的信息分析，合理的簡化，在反復(fù)提煉中建構(gòu)數(shù)學(xué)模型。

以人教版第十一冊第六單元百分?jǐn)?shù)中的“濃度問題”為例，“把含鹽量30%與5%的鹽水混合，得到20%的鹽水4 千克，求這兩種濃度的鹽水分別是多少千克？”學(xué)生分析數(shù)量關(guān)系，簡化出解決問題的關(guān)鍵信息：總鹽量不變，即第一種鹽水中鹽的質(zhì)量+第二種鹽水中鹽的質(zhì)量=混合后鹽的總質(zhì)量。引導(dǎo)學(xué)生運(yùn)用學(xué)過的方程，用這個基本模型解決此類問題：設(shè)其中一個量為x，則另一個量為（4-x），列出的方程為30%x+5%（4-x）=4×20%。解方程后，反思：“解法對嗎？符合題意嗎？該解法的優(yōu)缺點(diǎn)在哪里？能夠推廣嗎？還有其他解法嗎？”學(xué)生的模型思維能力得到強(qiáng)化和提高。此類濃度問題的實(shí)質(zhì)是溶質(zhì)質(zhì)量相等，大致的解題思路就是抓住溶液質(zhì)量與百分比的乘積等于溶質(zhì)質(zhì)量這一原理，再通過等量關(guān)系列出方程。讓學(xué)生經(jīng)歷尋找實(shí)際問題中數(shù)量之間的相等關(guān)系，正確列出等量關(guān)系式，整個解題過程條理清晰，同一類型問題解題模型的建立也就水到渠成了。

二、整合新舊知識，體會模型應(yīng)用

整合新舊知識并進(jìn)行類比推理時，重在溝通新舊知識間的聯(lián)系。先大膽猜想，再在直觀的事例中具體分析，不斷聯(lián)系所要解決的問題和已有的知識結(jié)構(gòu)，引導(dǎo)學(xué)生將之前所掌握的解題方法遷移到新的問題解決中來，建立新的解題模型。在觀察、比較中區(qū)分問題屬性的異同，并找出它們類似的特征，從而加深對新解法的理解。［2］

上述濃度問題，學(xué)生在嘗試運(yùn)用算術(shù)解法解答時遇到困難，教師可引導(dǎo)學(xué)生觀察方程解法中解方程的過程，設(shè)疑喚醒學(xué)生原有的知識：濃度5%的鹽水不是4 千克，為什么解方程過程中出現(xiàn)了4×5%？在解決哪類問題時，運(yùn)用到了哪種方法？你有什么猜想？學(xué)生在猜想是否把4 千克鹽水看成都是濃度5%的鹽水的過程中，聯(lián)想到“雞兔同籠”問題中的“假設(shè)法”，用假設(shè)法解釋濃度問題，將模型思想方法與自己以往的知識相聯(lián)系，將兩種問題整合在同一解題模型中。

假設(shè)混合后的4 千克鹽水濃度都是5%，那么應(yīng)該有鹽：4×5%=0.2（千克），實(shí)際有（4×20%=0.8）千克的鹽，比實(shí)際少算了：0.8-0.2=0.6（千克）。這是因?yàn)閷W(xué)生把濃度30%的鹽水都看成了濃度5%的鹽水，也就是濃度30%的鹽水每千克鹽水中所含的鹽的百分比少算了25%，正好多了0.6 千克。運(yùn)用對應(yīng)數(shù)量÷對應(yīng)分率，可以得到含鹽量30%的鹽水質(zhì)量，列式為：0.6÷（30%-5%）=2.4（千克），則濃度為5%的鹽水有：4-2.4=1.6（千克）。學(xué)生聯(lián)系“雞兔同籠”問題中的“列表法”，嘗試同相同方法解決濃度問題（見表1）。

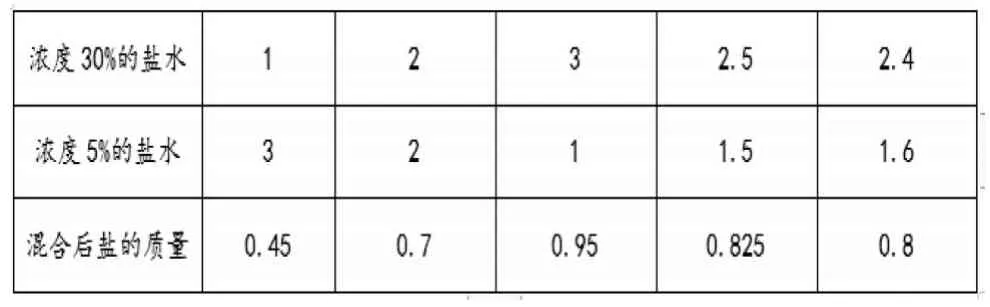
表1

從表1 中可以看出，每調(diào)整1 千克的溶液，溶質(zhì)相差（0.7-0.45）千克，混合后鹽的質(zhì)量是0.8 千克，比0.7千克多了0.1 千克，所以還需要調(diào)整0.1÷（0.7-0.45）=0.4（千克），2+0.4=2.4（千克）。

對比列表法在“雞兔同籠”問題中的運(yùn)用，學(xué)生發(fā)現(xiàn)：雞和兔的只數(shù)都是整數(shù)，用列表法較容易算出總只數(shù)；濃度問題中的鹽水質(zhì)量可能是小數(shù)，調(diào)整時要考慮到小數(shù)因素，需要推導(dǎo)出每次調(diào)整引起的數(shù)據(jù)變化，結(jié)合計(jì)算得出最后的結(jié)論。學(xué)生在新舊知識的整合中明確解題思路，在轉(zhuǎn)化的過程中化“生”為“熟”，化難為易，運(yùn)用假設(shè)的數(shù)學(xué)思想方法，歸納出解題模型：較大濃度鹽水=（鹽的總質(zhì)量-溶液總質(zhì)量×較小濃度）÷濃度差；較小濃度鹽水=（溶液總質(zhì)量×較大濃度-鹽的總質(zhì)量）÷濃度差；在運(yùn)用列表的數(shù)學(xué)方法中存同求異，體會模型的變化，建立相應(yīng)的解題結(jié)構(gòu)。

三、聯(lián)想創(chuàng)新，重構(gòu)新模型

對一個問題多角度的理解，能訓(xùn)練學(xué)生思維的廣闊性和靈活性。同樣是一道習(xí)題，一個知識點(diǎn)，不同的理念，不同的方法，會有不同的效率和價值。［3］在一定的簡化層次下，很多看起來完全不同的實(shí)際問題，可能有相同或相似的數(shù)學(xué)模型。此時，如果能引導(dǎo)學(xué)生展開聯(lián)想，啟發(fā)學(xué)生提出新思路、新設(shè)想，充分挖掘?qū)W生的創(chuàng)新思維能力，在創(chuàng)新過程中實(shí)現(xiàn)新的解題建模，則有利于推動學(xué)生思維的發(fā)展。

例如，學(xué)生結(jié)合課外學(xué)習(xí)所得，用圖示介紹解決混合濃度問題的另一種方法——十字交叉法：先寫出混合前的兩種濃度和混合后的濃度，交叉算出混合前與混合后的濃度差，再算出兩個濃度差的比值，最后把總質(zhì)量根據(jù)這個比值按比例分配求出原來兩種鹽水的質(zhì)量（如圖1）。

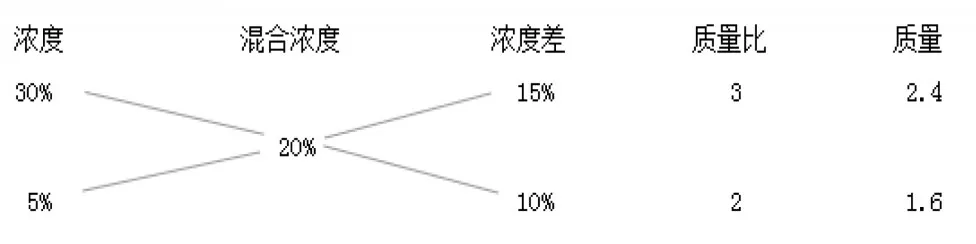
圖1

在理解“十字交叉法”解題模型的過程中，學(xué)生不知道為什么交叉的濃度差的比就是兩種鹽水的質(zhì)量比，教師引導(dǎo)學(xué)生采用假設(shè)法說明理由：假設(shè)兩種鹽水的濃度都是20%，則第一種鹽水中多了10%的鹽，這10%的鹽要補(bǔ)到第二種鹽水中，所對應(yīng)的就是第二種鹽水的質(zhì)量，所以才要交叉求出濃度差。學(xué)生聯(lián)想到用比例解決問題，創(chuàng)造出比例解題模型：

先分別求出濃度差：

30%-20%=10% 20%-5%=15%

再交叉算出濃度差的比：15%：10%=3：2

最后按比例分配分別算出兩種溶液：

在本環(huán)節(jié)模型思維拓展的過程中，教師注重引導(dǎo)學(xué)生發(fā)現(xiàn)知識、問題與方法的關(guān)聯(lián)性，歸納外在特點(diǎn)和內(nèi)在聯(lián)系，調(diào)整知識結(jié)構(gòu)，促使學(xué)生創(chuàng)新實(shí)踐，學(xué)生在理解解題模型的過程中，發(fā)現(xiàn)數(shù)量中的對應(yīng)關(guān)系，創(chuàng)造出新的解題模型。當(dāng)學(xué)生對具體的生活問題經(jīng)歷了一定的探索過程之后，便會發(fā)現(xiàn)數(shù)量之間的關(guān)系，生活問題便轉(zhuǎn)化為數(shù)學(xué)問題，綜合性地用數(shù)學(xué)模型解決問題，形成不同的解題策略。