基于生本課堂理念的小學數學高階思維培養

（龍巖市實驗小學，福建 龍巖 364000）

所謂“高階思維”，指的是發生在較高認知水平層次上的心智活動或者認知能力，包含創新能力、問題求解能力、決策力和批判性思維能力。培養學生高階思維，需要教師遵循生本課堂理念，也就是以學生的發展為本，培養學生獨立自主的學習能力，因此，在教學中，應將課堂還給學生，為學生提供分析、探究、延伸、評價的機會。在生本課堂理念下，教師需要在課堂留白，為學生創造自主思考的時間和機會；利用小組合作，激活學生創造性思維；尋求知識間的關聯，培養綜合求知能力；將評價交給學生，引導學生交流心得，［1］以培養學生的高階思維。

一、精心設問，培養問題求解能力

在傳統的課堂上，教師注重講授，注重知識的灌輸，學生沒有思考的時間和機會，只能對教師所傳授的知識進行記憶和全盤接受。而在生本課堂理念下，教師不再是課堂的中心，而是成為學生的伙伴，與學生一起組建“學習共同體”，為學生留白，給學生更多思考的時間和空間。［2］通過精心設問，引導學生分析思考，培養問題求解能力，使學生形成解題認知和對問題舉一反三的能力。

例題1 用9 個自然數能排成一個橫行、豎行、斜行相加和均為15 的魔術方陣（圖1），那么你能找出9個連續的自然數，排成一個橫行、豎行、斜行相加和均為18 的方陣嗎？請填寫圖2。

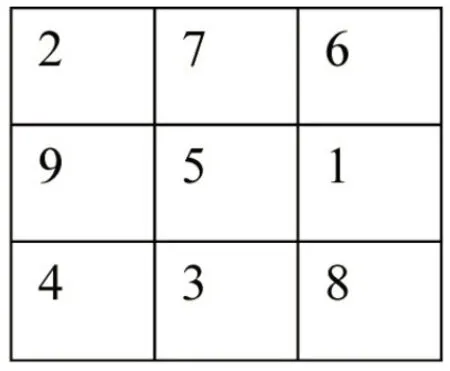
圖1

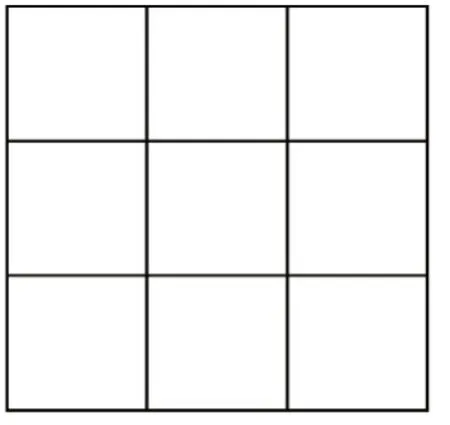
圖2

如果圖2 中已知幾個數字，求出其他數字相對比較簡單；但是在完全空白的圖中填入9 個數字，使其橫行、豎行、斜行相加和均為18，則具有一定的難度。針對這類題型，教師可以給學生做拓展，不是直接教給思路，而是引導學生思考其中的規律和解題方法。比如，以口訣的方法揭示其中的規律：“二、四為肩，六、八為足。上九下一，左七右三。”另外，還有口訣：“一居上行正中央，依次斜填切莫忘；上出框時向下放，右出框時向左放；排重便在下格填，右上排重一個樣。”通過設問并分析問題，提升學生的問題求解能力，有利于學生自主學習和解決問題，培養高階思維能力。

二、合作學習，激發創造性思維

創造性思維，是一種具有開創意義的思維活動，即開拓人類認識新領域、開創人類認識新成果的思維活動，是高階思維的一種體現。在培養學生創造性思維的過程中，可利用合作學習這一方式。在生本課堂理念下，教師積極組織小組合作學習活動，提前計劃合作學習的時間、地點、人數、活動內容、分工等，在合作中及時巡視、發現問題，引發學生的創造性思維。以《梯形的面積》教學為例，設計以下幾個環節：

1.梯度問題，合作突破難點。將學生在學習過程中所呈現出的難點作為合作的主題，為學生設置問題，問題要有一定的思維梯度，使學生能夠進行創造性的思考。例如，在教學《梯形的面積》時，教師沒有直接引入面積公式，而是提出問題：如何推導梯形的面積公式？然后讓學生小組合作探究，在組內交流、討論。

2.自主思考，形成獨到看法。小組合作學習要在學生獨立思考分析的基礎上展開討論。教師要鼓勵學生大膽剖析問題，明確自己的思路，再與同組同學進行討論。在小組合作推導梯形面積公式時，每個學生都有獨特的設想，教師可要求學生先自己觀察梯形，思考如何推導。［3］有的學生將梯形轉化為三角形和平行四邊形（圖3），也有的將梯形轉化為平行四邊形（圖4）。

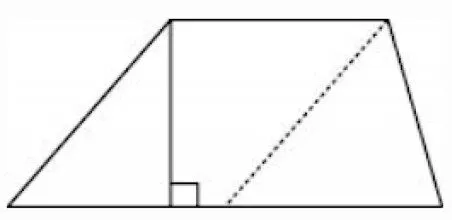
圖3

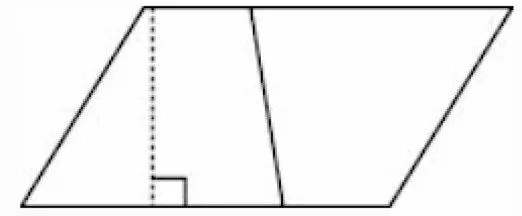
圖4

3.思維碰撞，構建知識體系。對于某一個問題，學生經過一定的思考后獲得認識，這些認識可能是片面的，也可能是錯誤的。在小組內討論和交流，是一個思維逐漸豐富、多元的過程。傾聽他人的思路，對比自己的思考，在交流中碰撞出火花，能夠激活高階思維，形成相對完善的解答，逐漸構建知識體系。

三、對比關聯，提升綜合求知能力

知識之間是相互關聯的。培養學生高階思維，必須讓學生尋找知識的脈絡、來源和走向，提升學生綜合求知能力，調動知識儲備進行對比聯想，延伸知識與鄰近區域的應用，尋找解決問題的最佳路徑。

例題2 李伯伯想要用20 根1 米長的木條圍成一個長方形的柵欄用來種花，如何才能使他圍成的柵欄面積最大呢？

解題思路通常分成三種：如何圍？能夠圍成幾種柵欄？最大的是哪一種？確立這三個解題步驟之后，引導學生尋找相關的知識脈絡：這道題用到哪些知識點？學生聯系到長方形的長、寬、周長、面積等內容。這道題本質上是已知長方形周長求面積的題目，學生通過對比聯想，進行綜合考慮，最終確立解決方案（見表1）。

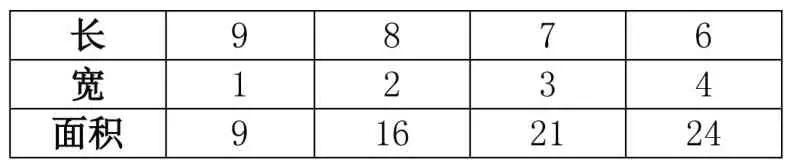
表1

由例題2 可知，長方形的周長：（長+寬）x2=20 米，因此長+寬=10 米，據此可列表格（見表2）：

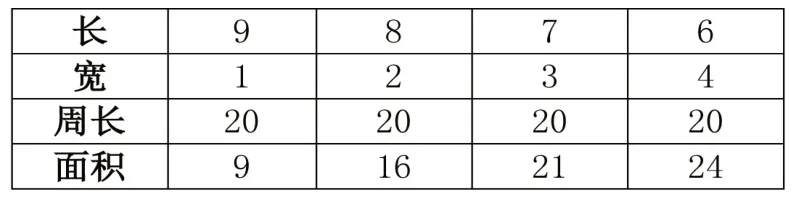
表2

由此可見，圍成的長方形的長與寬越接近，它的面積就越大。學生通過對案例的了解，對長方形長、寬、周長、面積等的對照，進行對比關聯，提升綜合求知能力。

四、評價、反思，發展批判性思維

批判性思維是通過一定的標準評價思維，進而改善思維，是合理的、反思性的思維。在課堂評價過程中，對于一些問題，教師不必急于評價，而是引導學生反思、質疑，讓學生之間就合作的內容、學習的情況、答案和解題思路等進行評價。在評價中，學生回顧所學內容，反思解題思路，通過對他人的評價，不斷反思自己的問題所在，以發展批判性思維能力。

例題3

140－50

140－75

140－32.5

140－x

問：x 在這里可以表示幾？

生1：x 可以表示自然數。

教師并沒有急于回答，而是讓其他學生對這個答案進行評價和質疑。

生2：x 必須要小于140。

生3：x 不只是小于140 的自然數，因為有個140-32.5，所以x 也可以是小數。

師：那么應該怎樣說？

生：140 以內的所有數。

學生一開始并沒有給出最準確的答案，教師沒有急于點評，而是把評價權交給學生，讓學生思考答案的準確性。學生經過不斷補充、完善后，得到最終的答案。完成這道題后，引導學生探討：再次遇到這類題型時，應該如何解答才能確保準確？讓學生交流、補充，有利于今后的解題思路更加明晰。