以社區發現為導向的網絡嵌入模型研究*

陳慧瑩 寇 月 申德榮 聶鐵錚

（東北大學計算機科學與工程學院 沈陽 110819）

1 引言

社交媒體網絡包含了豐富的網絡信息。聯系緊密的個體及其關聯關系形成了社交網絡中的社區結構。傳統的網絡分析方法難以處理復雜多樣的數據且易丟失豐富的節點信息。網絡表示學習是將蘊含豐富信息的數據表示成簡單低維的向量形式，并且同時直觀高效的保留原有的特征信息。如圖1所示，節點1與節點2、節點12原本分屬兩個不同的社區。若采用傳統的網絡嵌入方法，將可能導致三個節點被劃分為同一個社區。原因在于忽略了節點固有的社區結構。對于同屬于一個社區的節點，應該比隸屬于不同社區的節點更加相似。因此，考慮節點所體現出的社區特征，可以提高社區劃分的準確性。現有少數網絡嵌入方法考慮了網絡固有的社區結構。例如，文獻［1］在網絡嵌入時考慮了社區特征，但沒有將社區特征與節點屬性特征相結合。文獻［2］也通過非負矩陣分解保持了社區結構，但其目標在于學習節點的嵌入表示，而非社區發現。針對以上不足，在學習節點的嵌入表示時，同時考慮節點屬性特征和社區特征，并且將嵌入表示應用到社區發現中，以提高社區劃分的準確性。貢獻如下：

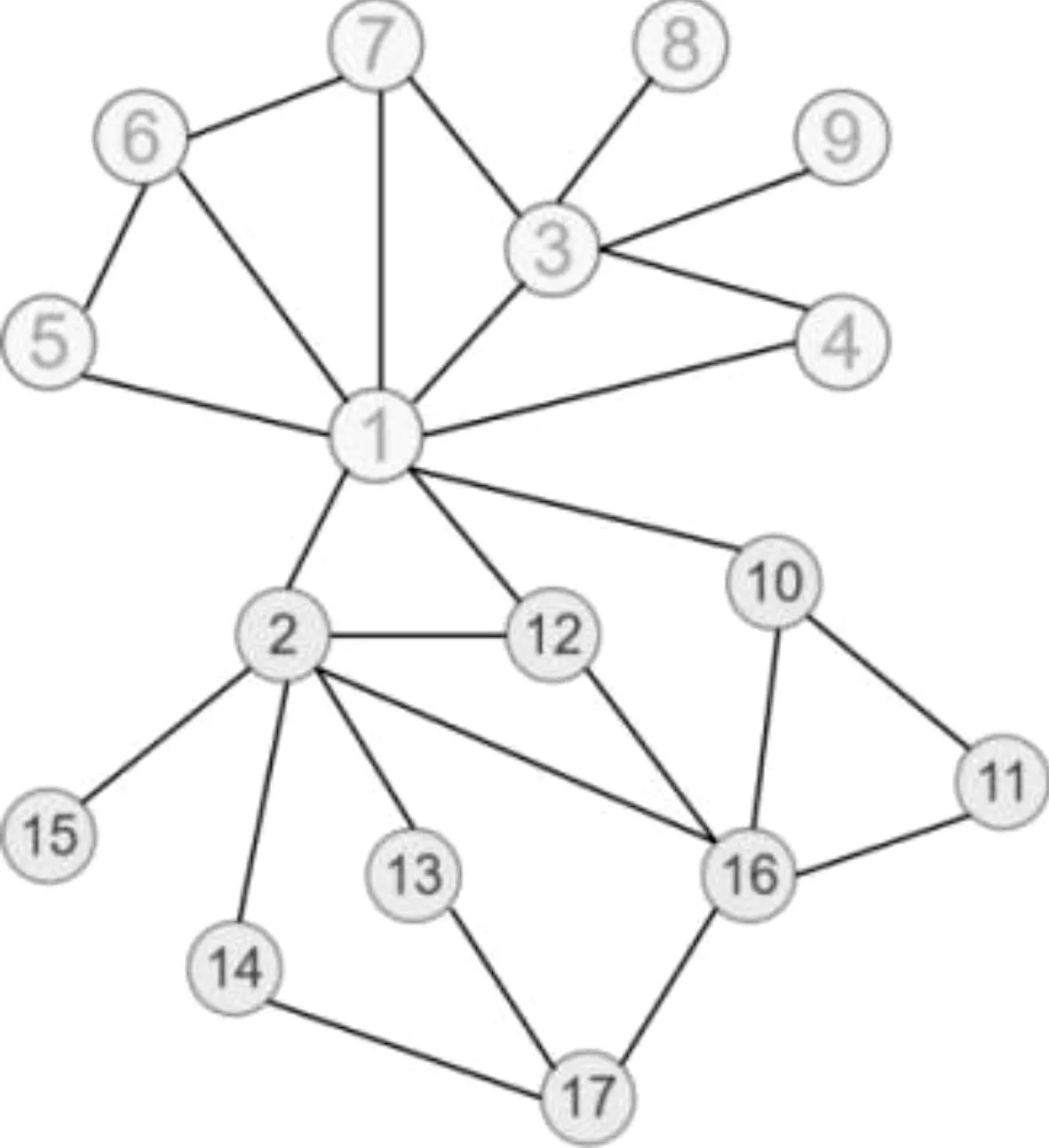
圖1 具有社區結構的網絡

1）提出了一種以社區發現為導向的網絡嵌入模型（Community Detection-oriented Network Embedding，CDNE）。與傳統模型不同，該模型同時考慮了節點屬性特征和更高階的隱含特征（即網絡中固有的社區特征），同時體現了網絡的局部特征與全局特征。

2）提出了一種基于CDNE的兩階段社區發現算法。第一階段為合并社區；第二階段基于待合并社區重新構建網絡。通過兩個階段的交替迭代執行，來提高社區發現的準確性。

3）在真實數據集上設計對比實驗，證明了該方法具有一定的優勢。

2 相關工作

本節首先介紹了社區發現、網絡表示學習的相關工作并作出了比較。

早期Girvan等提出了GN算法［3］，該算法采用邊介數代表邊的強弱，通過不斷移除網絡中邊介數最大的邊得到社區結構。Newman等提出基于模塊度Q的區挖掘算法［4］，該算法應用了貪婪思想。Bagrow提出了一種局部社區結構發現算法［5］。2013年，Yang等提出CESNA算法［6］，有效提高社區劃分的質量。Yang等提出了一個條件模型來進行鏈接分析以及一個歧視性模型來進行內容分析［7］。

傳統的網絡表示學習都是針對同質信息網絡。異質信息網絡中包括基于隨機游走、分解和針對應用任務的網絡表示學習。Yu［80］等作者提出了基于元路徑［9］的Metapath2vec算法。Tang［10］等提出分解的思想，將異構文本網絡中復雜的數據轉化為簡單高效的表現形式。Sun［11］等首先研究異質信息網絡中同一類型頂點上的相似搜索方法Path-Sim。

本文提出的技術與上述不同之處在于：傳統的社區發現算法極少考慮到網絡中更高階的社區結構對社區發現的重要性。因此提出一種以社區發現為導向的網絡嵌入模型。此外，許多方法都采用傳統的網絡存儲方式耗費了較高的存儲資源，考慮的特征也很單一，因此本文通過網絡嵌入將拓撲特征，屬性特征以及社區特征有效地綜合起來，應用到社區發現當中，提高劃分的準確性。

3 問題定義

定義1（屬性網絡社區發現問題）旨在從圖中G(V，E，W，S)找到T∈Rn×n個社區，其中T∈Rn×n表示T∈Rn×n個節點的集合，T∈Rn×n是邊的集合，T∈Rn×n表示邊T∈Rn×n的權重。S表示節點的屬性矩陣。并且理想的社區發現結果需滿足相同社區內的節點屬性特征相似，不同社區內的節點屬性相差較大。

定義2（網絡嵌入）定義圖T∈Rn×n，對所有節點T∈Rn×n，學習映射關系T∈Rn×n，將原節點表示成一個低維稠密的實數向量T∈Rn×n。

定義3（節點表示矩陣）節點表示矩陣T∈Rn×n，通過網絡嵌入方法得到節點低維的向量表示T∈Rn×n。

4 以社區發現為導向的網絡嵌入模型

為了充分利用并整合網絡的多種特征，以提高社區發現的準確性，提出了一種以社區發現為導向的網絡嵌入模型——CDNE。

4.1 CDNE模型的基本思想

模型有兩大部分組成：保持社區特征的網絡嵌入以及基于網絡嵌入的社區劃分（如圖2所示）。網絡中往往蘊含了大量的信息，其中節點也具有豐富的屬性特征。同時，網絡中也可能存在原有的一些社區結構。模型將這三種特征有機地結合起來，通過非負矩陣分解方法得到節點的低維表示。然后使用Louvain［12］社區發現算法完成社區劃分。

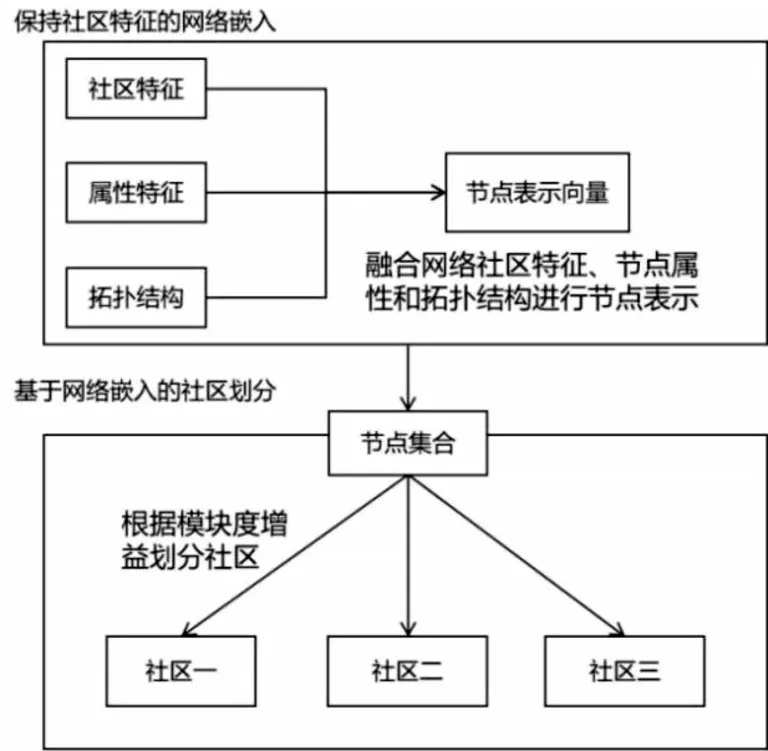
圖2 社區為導向的網絡嵌入模型CDNE

4.2 保持社區特征的網絡嵌入

在原始網絡中，從宏觀上看，網絡本就存在其固有的社區結構，某些節點屬于同一潛在的社區結構。

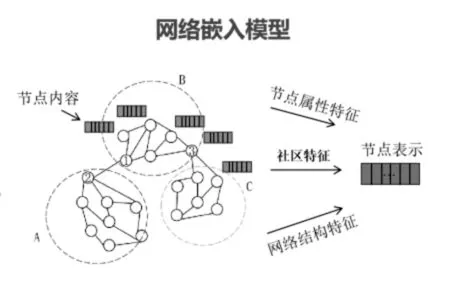
圖3 網絡嵌入

1）保持社區特征的學習

首先，找到關系矩陣進行分解來獲得節點在低維空間中的映射。定義了模塊化矩陣B∈Rn×n，滿足式（1），其中Ki，Kj代表的是點i，j的度數，e代表的是邊的數目。

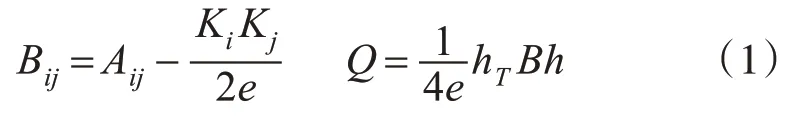
其中h=[hi]∈Rn是社區成員隸屬度向量。將社區成員隸屬度表示為矩陣H∈Rn×k。因此有約束t r(HT H)=n，得到了式（2）：

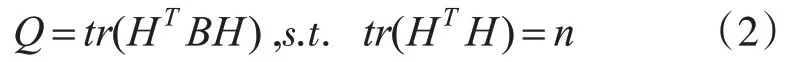
2）保持屬性特征的學習

社區不僅具有緊密連接的結構，而且同一社區應該具有相似的屬性。不同的社區也偏好不同的屬性。定義節點的余弦屬性相似度矩陣T∈Rn×n。

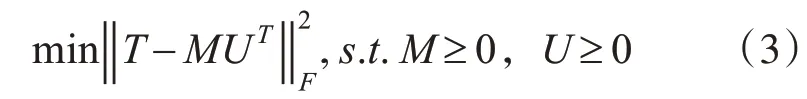
如式（3），通過分解屬性相似度矩陣ΔQ來得到節點表示矩陣U∈Rn×n，另引入一個輔助非負矩陣Ci即第i行表示一個社區的表示向量。因此進行聯合建模，聯合損失函數如式（4）：

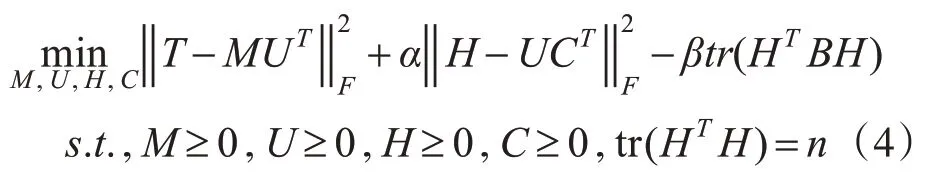
此外，通過控制非負參數α，β的大小來調節兩種特征的貢獻程度。目標函數的優化采用M-NMF中的迭代更新規則進行優化。

5 基于網絡嵌入的兩階段社區發現算法

基于CDNE模型，首先提出一種社區發現算法，該算法在Louvain算法的基礎上進行改進。

5.1 第一階段：合并社區

Louvain算法具有快速、準確的優點。但該算法忽略了網絡中固有的社區結構，只考慮節點間的鏈接關系。針對它存在問題，本文考慮將節點屬性和社區特征應用到Louvain算法中，實驗證明在真實網絡中可以提高社區劃分的準確性。

學習到節點的嵌入后，計算節點i與j向量的余弦相似度S(i，j)并作為節點間邊的權重。每個節點都當做社區，遍歷所有節點，將當前節點i分別加入每個鄰居節點所在的社區并計算加入前后模塊度的變化。根據模塊度增量ΔQ最大值將該節點i分配至對應的鄰居節點社區，直至網絡中所有節點的分配穩定得到初步劃分好的網絡。

5.2 第二階段：重構網絡

這時將社區當做一個新節點重構網絡，分別計算這些新節點之間的連邊的權重，其值為先前網絡中跨社區之間連邊的相似度之和。重復階段一直到節點的社區分配基本穩定，得到融合社區特征和節點屬性特征的網絡社區近似最優劃分。

5.3 算法描述

基于網絡嵌入的兩階段社區發現算法過程如下。

算法1 基于嵌入的社區發現算法輸入 屬性網絡G；

輸出 G的社區劃分結果partition

1 For each node｛u，v｝∈E

2 Calcualte node similarity Cs；

3 End

4 Initialize each node into individual communities and calculating modularity，denoted by Q；

5 For each i in｛v｝

6 Calculate the neighbors｛k｝of node i；

7 For（j in neighbors｛k｝）

8 Delete node i from the pre_community；

9 Add node i into communoty of neighbor j

10 CalculateΔQ；

11 Choose the maximumΔQ and add the node i into the new community ofΔQ；

12 Calculate Q；

13 End

14 Regard each community as a new node and repeat the above steps；

15 Return the result；

6 實驗與結果

6.1 實驗數據集

本文在Cornell、Wisconsin和Texas三個數據集上進行實驗，三個數據集統計信息如表1所示。

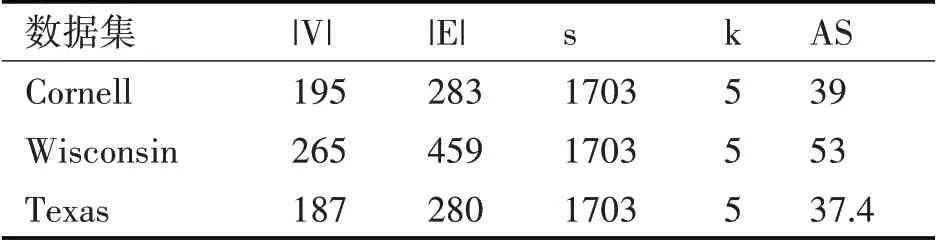
表1 實驗數據集的統計信息

|V|代表節點數，|E|代表邊數，s代表屬性數量，k代表社區數量；AS代表社區的平均大小。

6.2 評價指標

NMI是一種常用的評價社區發現算法精度的指標。模塊度是根據社區內部節點和邊的疏密程度來量化社區結構的質量。

6.3 對比算法

基于初始結構的Louvain算法。SCI算法［13］提出了一種非負矩陣分解模型。SNMF［14］是一種基于非負矩陣分解的社區發現算法。PCL-DC［15］是一種綜合鏈接和內容的社區發現算法。

6.4 對實驗結果與分析

1）參數敏感性分析

以下在Cornell數據集上進行了CDNE的參數敏感性分析。α，β分別控制節點屬性、社區特征的貢獻度；由圖可知，當α=1，β=2時可取到NMI最大值為0.368。

2）對比算法實驗結果分析

本文將CDNE與四種基線算法做了性能比較。采用NMI和模塊度兩種評價指標來衡量。圖5中結果表明CDNE算法都明顯要優于其他算法。相比較可知，通過網絡嵌入融合社區特征與節點屬性特征有效地提高了社區發現的準確性。

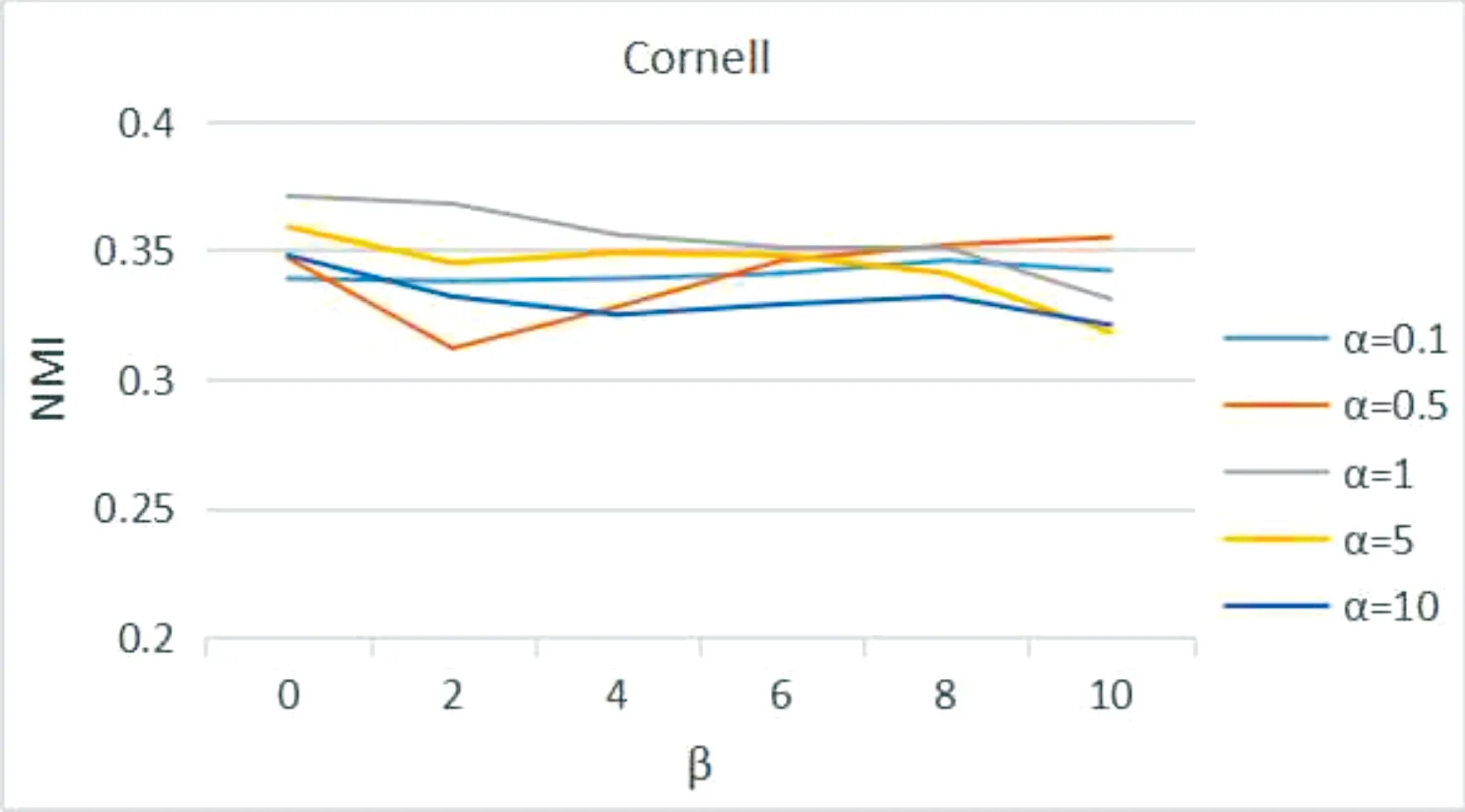
圖4 Cornell中參數α，β對NMI的影響

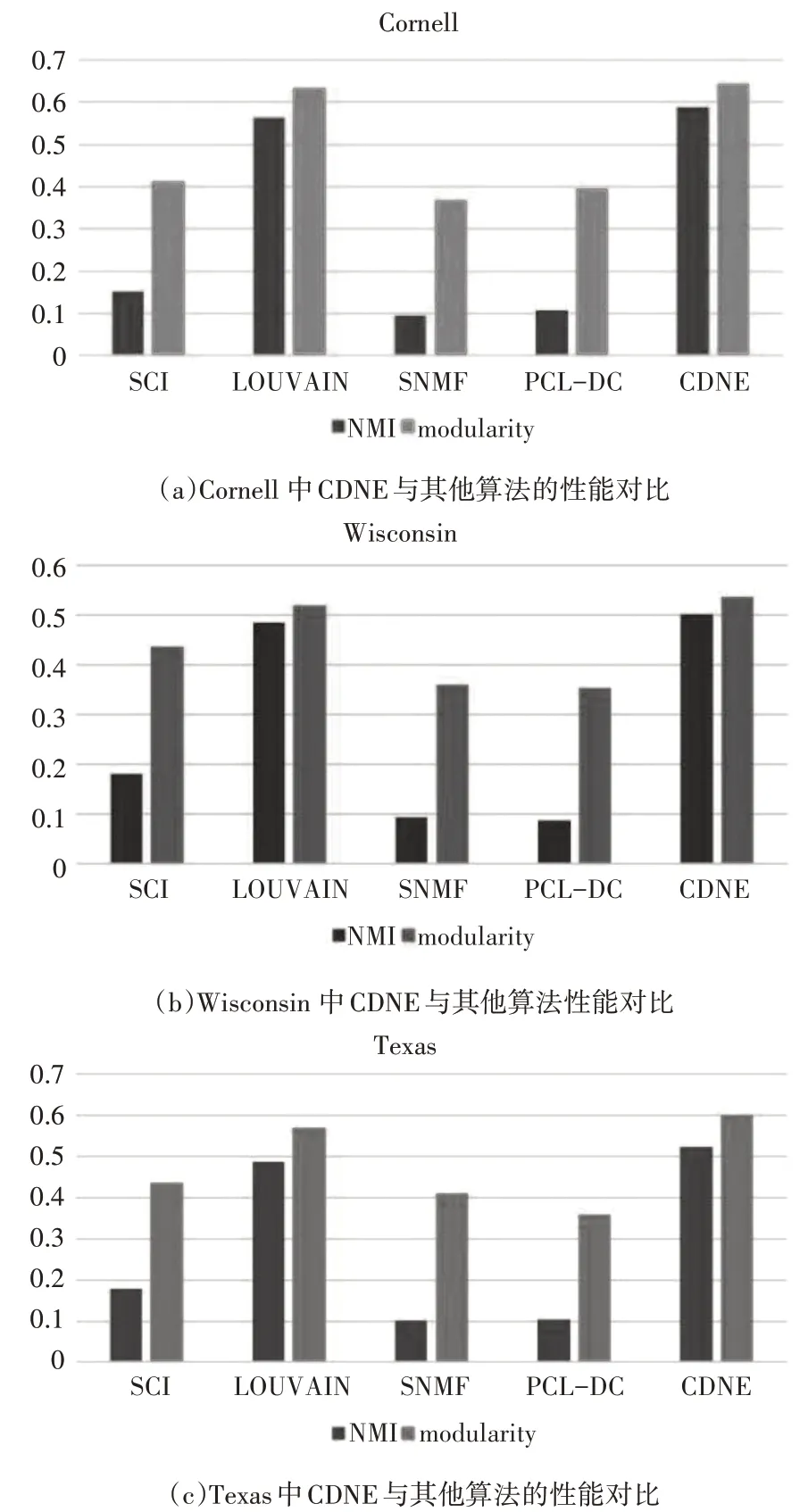
圖5 對比算法實驗結果分析

7 結語

針對現有的社區發現算法的不足，本文提出了一種以社區發現為導向的網絡嵌入模型（CDNE），充分考慮了網絡中的社區特征，節點屬性信息，利用非負矩陣分解將三者有機地融合起來。此外本文提出基于網絡嵌入的兩階段社區發現算法。采用Louvain算法進行社區劃分，融合社區特征和節點屬性特征的同時有效地提高了社區發現的準確性。