翼型凹變對風輪旋轉噪聲影響特性分析

呂文春， 汪建文， 段亞范， 馬劍龍， 孟克其勞， 陳金霞

(1.內蒙古工業大學 能源與動力工程學院，呼和浩特 010051；2.內蒙古機電職業技術學院 科技與職教研究中心，呼和浩特 010070；3.內蒙古自治區高等學校 可再生能源工程研究中心，呼和浩特 010051；4.風能太陽能利用技術教育部重點實驗室，呼和浩特 010051)

隨著分散式風電的快速發展，越來越多的風力機安裝在離負荷中心區域較近且風能密度較高的地區。然而風力機在運行中產生的噪聲問題則嚴重影響了當地居民的正常生活，成為阻礙分散式風電發展的一個重要因素。風力機在運行中的噪聲主要分為機械噪聲和氣動噪聲，其中機械噪聲已經得到很好的控制。因此，如何降低風力機的氣動噪聲問題則變的尤為重要。

目前，國內外學者為解決風力機的氣動噪聲問題進行了大量研究。其中，研究的方向多集中在葉片翼型自噪聲和旋轉噪聲等方面。翼型自噪聲主要包含尾緣噪聲、失速噪聲和層流渦噪聲等[1]。其中，對于尾緣噪聲的研究相對較多。尾緣噪聲是由葉片表面的湍流邊界層流經尾緣并相互作用而產生[2]。因此，針對尾緣噪聲常用的降噪方法就是控制葉片吸力面湍流邊界層的生成或對翼型尾緣進行結構優化等。而對于湍流邊界層的控制，主要是通過擾流實驗探究湍流強度、攻角及來流雷諾數等對湍流邊界層生成的影響[3-5]，并通過改變翼型厚度或在吸力面采用抽吸孔、脊狀結構及添加粗糙元等方式延遲翼型吸力面湍流邊界層的生成[6-8]。相關典型研究有：王松嶺等通過在翼型吸力面增加脊狀結構有效改善邊界層分離狀況，并減小了翼型表面的壓力脈動；Jelinek等探究了平面粗糙元對邊界層的轉捩現象的影響。對于葉片尾緣結構優化方面，主要是通過改變葉片尾緣的形狀從而破壞脫落渦結構，起到降噪效果。目前對尾緣的結構優化方式有很多種，比如鋸齒狀、波浪形，鈍尾緣或添加襟翼等[9-12]。典型研究有：Arce Leon等探究了鋸齒尾緣對葉片氣動噪聲的影響；蘇彩虹發現波浪形尾緣可以有效降低葉片的寬頻噪聲。

在風輪旋轉噪聲方面，風輪旋轉噪聲是由于葉片經過流體時產生周期性漲縮作用和葉片上載荷力的作用形成，且噪聲頻率與風輪轉速相關[13]。相關研究有：Wasala等[14]發現水平軸風力機風輪旋轉產生的噪聲為主要噪聲，且聲壓級較高；李運志等[15]發現風輪的旋轉噪聲頻率主要集中在200 Hz以下，并確定了聲源位置。陸贇韜[16]發現旋轉噪聲的強度與葉片對流場的擾動有關，隨著振動幅值的增大而增強。

綜合國內外文獻可知，目前對風力機氣動噪聲的降噪方法多集中在翼型自噪聲方面，而針對風輪旋轉噪聲的降噪方法研究還相對較少。在以往研究中發現翼型凹變可以提升葉片的結構特性并且有效延遲葉片吸力面氣流的轉捩位置，提高葉片的氣動性能[17]，然而翼型凹變對風輪氣動噪聲的影響以及影響原因還未揭示。因此，本文針對聲壓級較高的旋轉噪聲進行分析，探究了翼型凹變對風輪旋轉噪聲的影響。并從結構場出發解析了翼型凹變對風輪旋轉噪聲影響的原因。

1 旋轉噪聲測試及分析

1.1 測試系統及方法

測試對象為某S翼型水平軸風力機三葉片風輪，風輪直徑為1.4 m。實驗在內蒙古工業大學B1/K2式風洞開口實驗段進行，聲數據的采集及處理由B&K公司的60通道圓形聲陣列系統完成。其中，聲陣列直徑為0.78 m，傳聲器的靈敏度為12.5 mV/Pa，測量范圍為10～20 000 Hz。風輪轉速通過直流電子負載調節，其精度為0.1%+0.1%FS，并利用Fluke實時監測功率和轉速等參數。在測試中，聲陣列盤平行風輪放置，并放置在風輪下風向的后方0.2 m處，實驗采用SONAH算法進行處理分析，測試設備安裝如圖1所示。

圖1 測試設備安裝圖

1.2 凹變葉片形式確定

翼型凹變葉片是在原翼型的基礎上，通過翼型繞流實驗確定吸力面的轉捩位置而進行凹變得到。凹變的方式及長度則通過功率實驗確定。經過測試發現凹變位置在其吸力面0.8倍弦長處，凹槽長度為350 mm時風輪輸出功率最高[18]。以圖2(a)中某翼型為例，假設流動的分離點常常出現在M處，則選定M處為翼型凹變中心。考慮到翼型弦長顯著大于其最大厚度，嘗試將翼型凹變的幾何結構采用橢圓形。

令橢圓中心為M位置，橢圓長軸為弦長的7.2%、短軸為弦長的3.6%，并使橢圓長軸與M處原翼型曲線相切，凹變部分與非凹變部分之間采用樣條曲線連接，具體過程如圖2(b)所示。

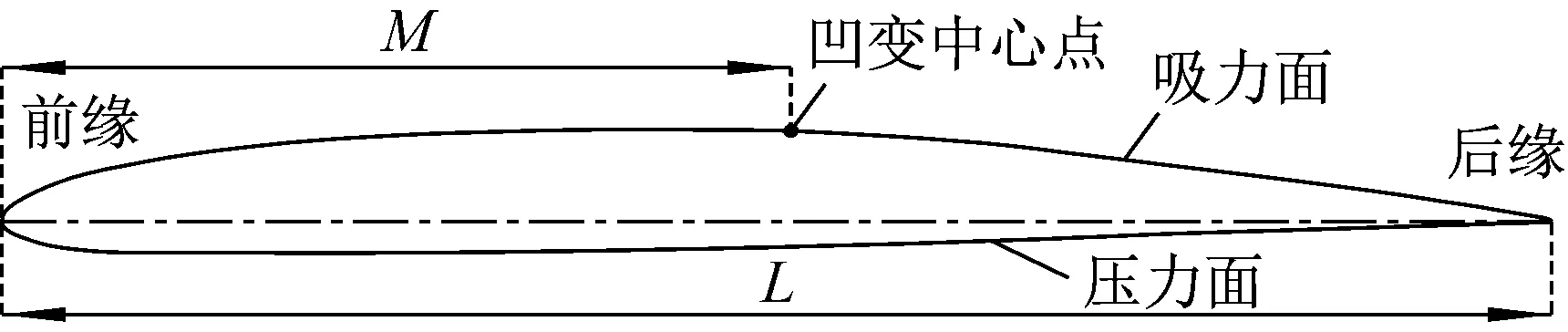
(a) 原翼型

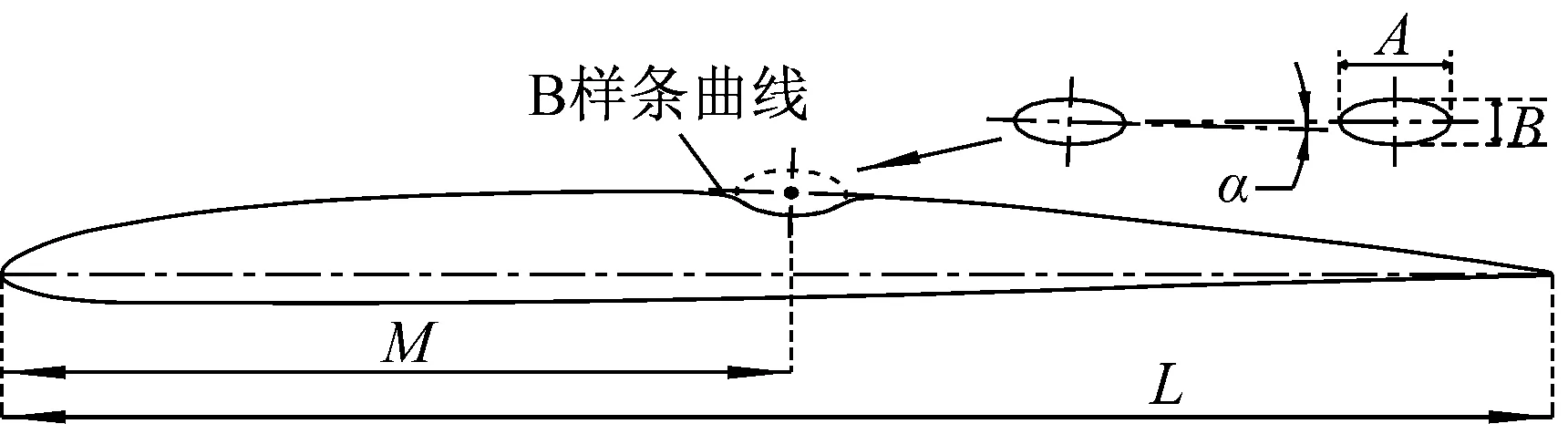
(b) 凹變翼型

圖2中：L為翼型弦長；M為凹變中心點到翼型前緣點的距離；A為橢圓長軸；B為橢圓短軸。

原翼型葉片和翼型凹變葉片實物如圖3所示(其中原翼型葉片表示為A，翼型凹變葉片表示為B)。

1.3 對旋轉噪聲測試結果分析

1.3.1 背景噪聲分析

聲信號在測量中有包括風洞運行在內的環境背景噪聲，會對風輪旋轉噪聲的準確獲取產生干擾，因此在測試前需進行背景噪聲測試。背景噪聲測試中，不安裝風力機，陣列盤的測量位置與安裝風力機的測試位置相同。

圖3 葉片實拍圖

風輪的旋轉噪聲采用SONAH算法進行分析，聲信號處理中不做常規計權處理，并在處理過程中采用恒定頻域(1 Hz)分析，以確保達到細化頻譜的目的。

以來流風速為9 m/s為例，近場背景噪聲測試如圖4所示。由圖4可知，風洞在低頻(200 Hz)以內的主要噪聲是由風洞入口處軸流式引風機葉片的旋轉噪聲(77 Hz)及其諧波構成。

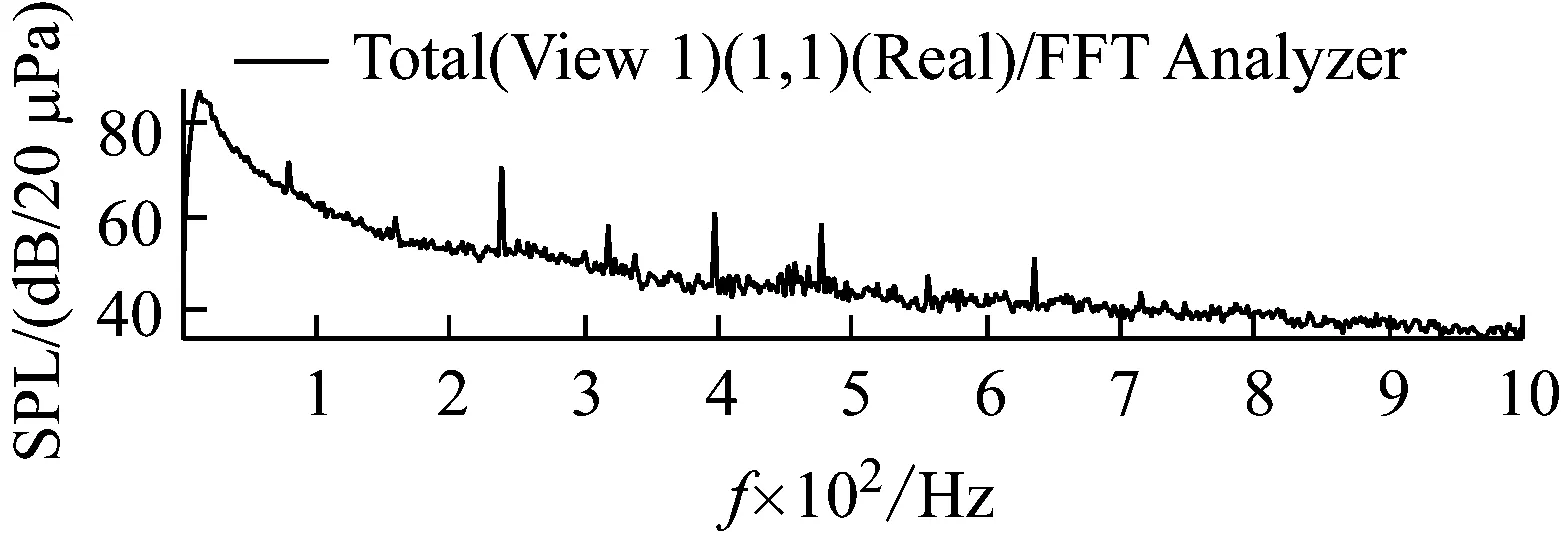
圖4 近場背景聲頻譜分布圖

1.3.2 對旋轉噪聲分析

以風速為9 m/s,轉速為600 r/min的工況為例，得到風輪旋轉噪聲聲壓級頻譜圖，如圖5所示(其中f為旋轉基頻,2f為旋轉2倍頻，3f為旋轉3倍頻，4f為旋轉4倍頻)。

(a) A 葉片

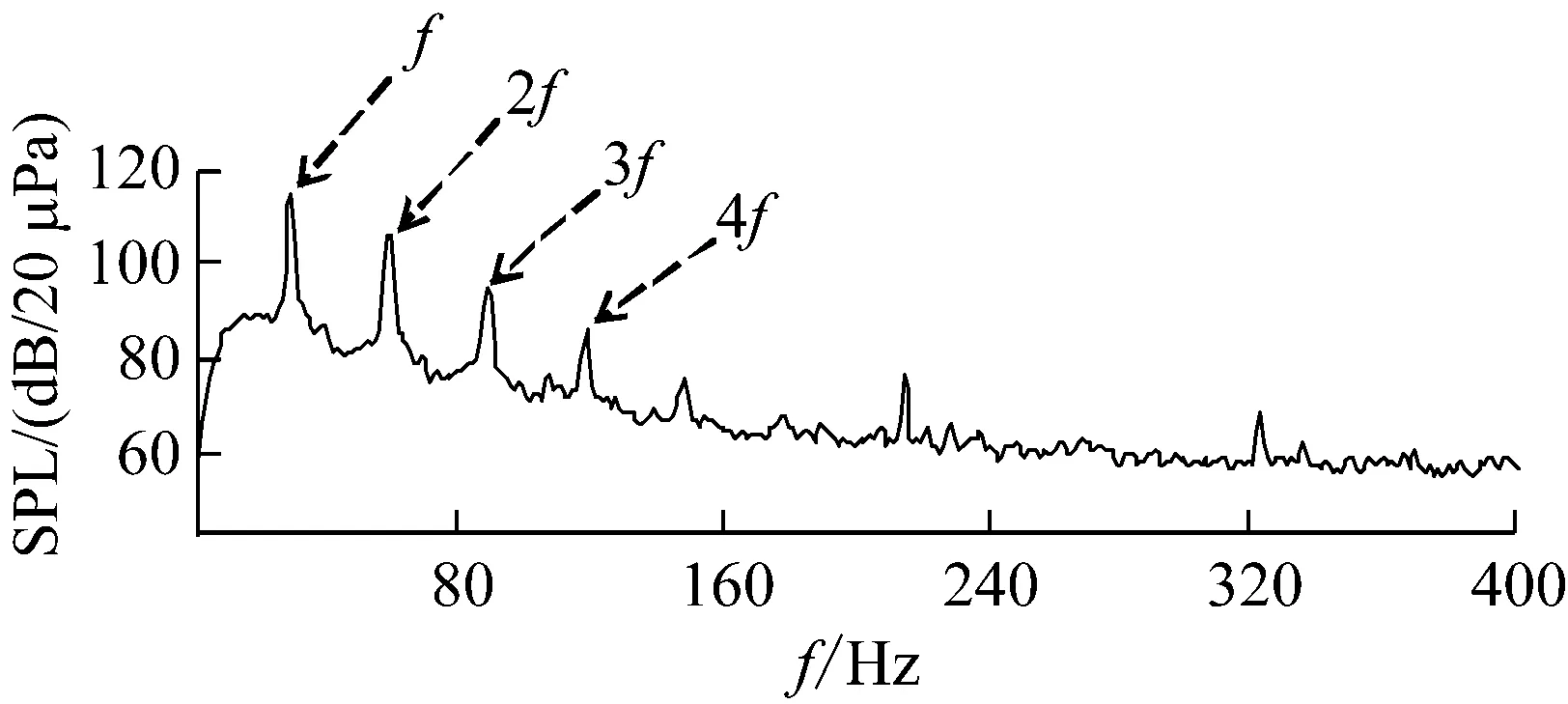
(b) B 葉片

通過對圖5分析發現，旋轉噪聲主要由基頻及其倍頻諧波組成，且頻率主要位于200 Hz以內。另外，在聲頻譜圖中除旋轉噪聲外還有其它噪聲峰值，通過聲源識別發現此處的噪聲峰值為電機機艙噪聲，因此不對其進行分析。

為了探究翼型凹變對旋轉基頻及其倍頻諧波聲壓級的影響，本文提取不同工況下倍頻諧波的聲壓級進行分析，如表1、2所示(以轉速600 r/min和風速9 m/s為例)。

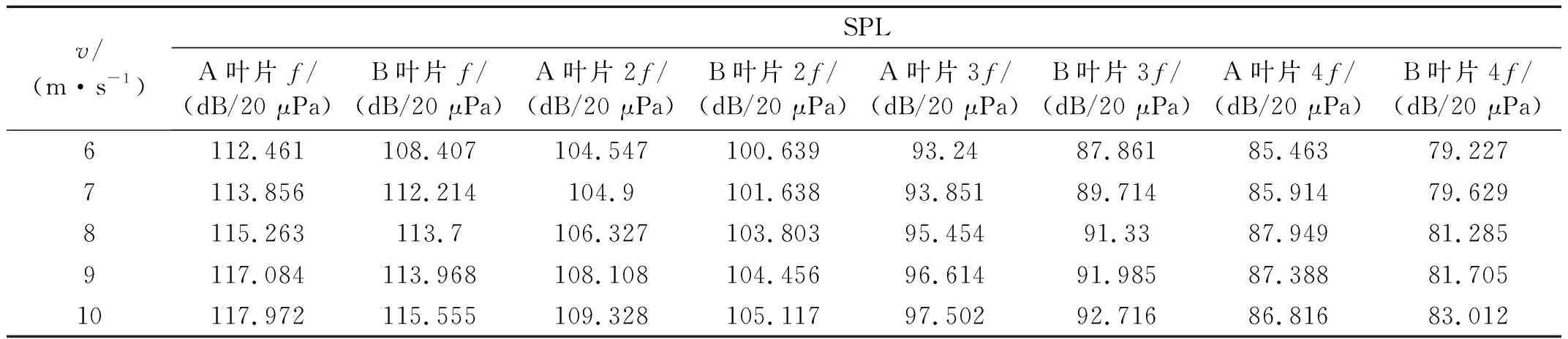
表1 風速變化對葉片旋轉噪聲的影響

表2 轉速變化對葉片旋轉噪聲的影響

通過對葉片旋轉噪聲隨工況變化分布表分析發現，在相同工況時，B葉片旋轉噪聲的聲壓級均明顯低于A葉片，說明翼型凹變后可以明顯降低葉片的旋轉噪聲。另外發現，旋轉基頻的噪聲聲壓級最大，其倍頻聲壓級隨著倍頻次數的增加而逐漸減小。同時，當轉速相同時，旋轉噪聲的聲壓級隨著風速的增加而逐漸增大，而當風速相同時，旋轉噪聲的聲壓級隨著轉速的增加呈現出先升高后降低的趨勢。

為了探究在相同工況下，翼型凹變對葉片旋轉基頻及其倍頻噪聲的影響變化。本文以式(1)來表示在相同工作條件下，翼型凹變引起聲壓級的變化值。

φi=SPLA葉片，i-SPLB葉片，i

(1)

其中(i=1、2、3、4)分別表示旋轉基頻和第二、三和四次倍頻諧波。為了分析翼型凹變對不同倍頻諧波聲壓級影響的敏感性，本文在相同工況下用式(2)定義參數ψ，如圖6所示(以風速9 m/s，轉速600 r/min為例)。

(2)

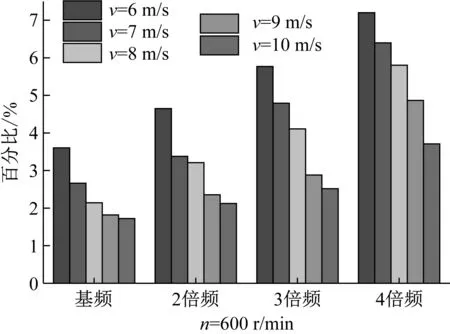
(a) 風速變化對不同倍頻聲壓級的敏感性影響

(b) 轉速變化對不同倍頻聲壓級的敏感性影響

通過對圖6分析發現，在相同工況下，翼型凹變對葉片不同倍頻諧波噪聲的敏感性隨著倍頻次數的增加而逐漸增強，最高可達7.2%。另外，當轉速相同時，翼型凹變對不同倍頻諧波噪聲的敏感性隨著風速的增加而逐漸減弱。而當風速相同時，翼型凹變對葉片不同倍頻諧波噪聲的敏感性隨著轉速的增加呈現出先增強后減弱的趨勢，且當n=550 r/min時，翼型凹變對葉片不同倍頻諧波噪聲影響的敏感性最強。

通過以上分析發現，不同倍頻諧波噪聲受翼型凹變影響的變化趨勢相似，只是影響的敏感性不同。由于在葉片旋轉噪聲中旋轉基頻噪聲的聲壓級最高，因此本文重點對葉片旋轉基頻噪聲進行分析。

1.3.3 對旋轉基頻噪聲分析

以風速為8 m/s、9 m/s、10 m/s和轉速600 r/min、650 r/min、700 r/min等工況為例，對其旋轉基頻噪聲進行分析，如圖7所示。

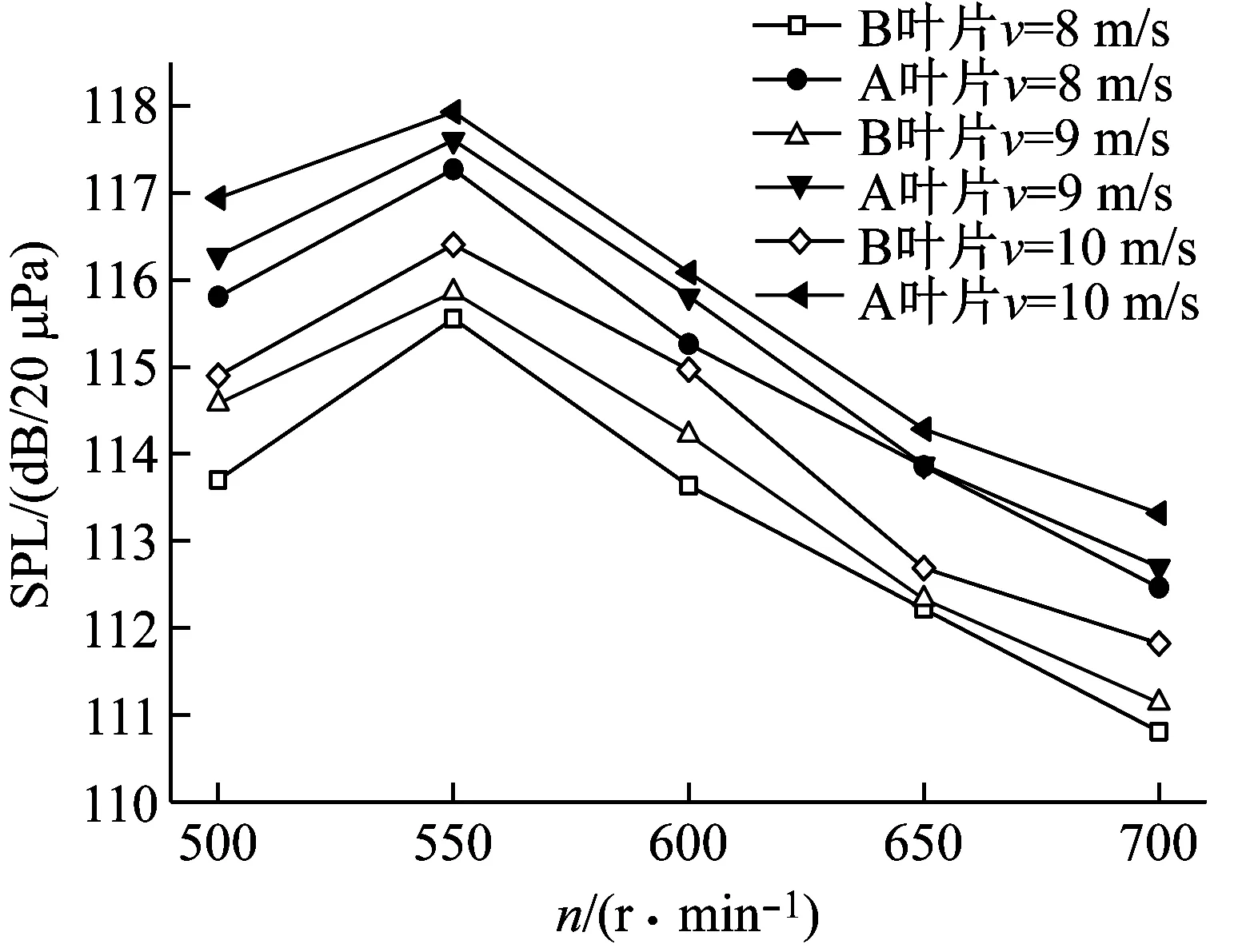
(a) 風速變化對葉片旋轉基頻噪聲的影響

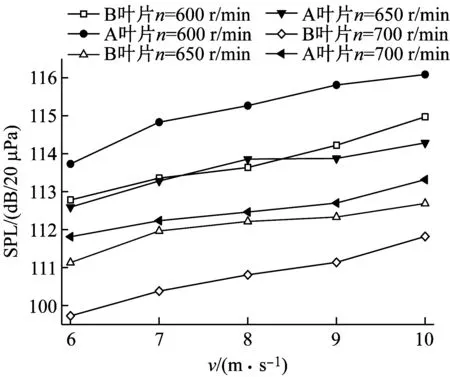
(b) 轉速變化對葉片旋轉基頻噪聲的影響

通過對圖7分析發現，翼型凹變后只是降低了旋轉基頻噪聲的聲壓級，卻沒有改變旋轉基頻噪聲隨工況的變化趨勢。即當風速相同時，旋轉基頻噪聲的聲壓級隨著轉速的增加呈現先升高后降低的趨勢，且峰值均出現在轉速為550 r/min的工況處，而當轉速超過550 r/min時聲壓級逐漸降低。分析原因發現，此刻風輪受離心鋼化作用影響明顯，導致葉片剛度增加從而減弱了葉片受氣動載荷的影響。同時，在相同轉速下葉片的旋轉基頻噪聲的聲壓級隨著風速的增加而逐漸增大，說明風輪旋轉基頻噪聲與氣動載荷之間呈正相關性。

2 對風輪旋轉噪聲降低原因分析

風輪的旋轉噪聲是由于風輪與周期性來流相互作用以及對表面流體的漲縮作用而產生。因此，本文從結構場出發，分別對原葉片和凹變葉片進行結構動態測試，并通過分析翼型凹變對風輪葉片剛度及動頻的影響，探究了翼型凹變降低風輪旋轉噪聲的原因。

2.1 翼型凹變對剛度的影響

2.1.1 測試系統及方法

測試系統采用B&K公司研發的PULSE結構振動分析系統，該系統的最大誤差不超過2.8%。測量時，在葉片壓力面兩側均勻布置8個單向加速度傳感器。測試方法采用瞬態激振法，單點激勵，多點響應。振動頻率采集范圍設置為0～400 Hz。加速度傳感器的布置方式及激勵點如圖8所示。

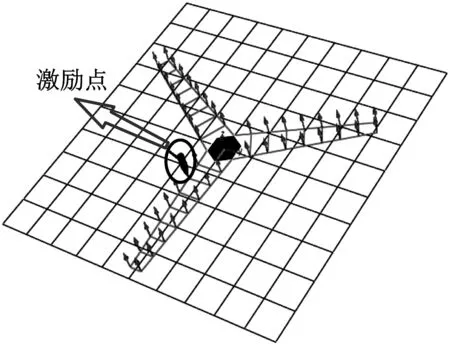
圖8 風輪剛度測試模型圖

2.1.2 風輪剛度測試結果分析

將數據導出到Reflect中進行后處理分析得到A葉片與B葉片所對應各階的振動頻率及阻尼比，如表3所示。

表3 風輪振動固有頻率及阻尼比

從表3中可以得出，B葉片較于A葉片在軸向竄動、一階反對稱、一階對稱的固有頻率分別有1.16%、1.45%和0.48%的增加。分析其原因：當葉片被力錘敲擊時的振動形式，可以看做為一個單自由度有阻尼的振動形式。

則葉片的固有頻率

(3)

式中:f為固有頻率；k、m為剛度與質量；ζ為阻尼比。

則葉片靜剛度

(4)

通過對葉片稱重發現，翼型凹變后葉片質量減少了1%，由表3可知，翼型凹變后葉片的固有頻率和阻尼比都得到較大的提升。因此，翼型凹變后可以有效的增加葉片的靜剛度。另外發現，翼型凹變后葉片軸向竄動和一階振動阻尼比的提高使得葉片振動消減速度變快，即在相同工況下翼型凹變葉片的疲勞損失也會有一定程度的下降。

2.2 翼型凹變對風輪動頻的影響

2.2.1 測試方法和傳感器測試點分布

測試方法采用布置于發電機前端部靠近風輪處的加速度傳感器捕獲振動頻譜，通過已獲得的模態數據結合譜分析法識別風輪動頻，傳感器布置如圖9所示。

圖9 傳感器布置

2.2.2 動頻識別

通過對2個不同位置的傳感器動態頻譜圖分析發現，布置在發電機頂部前端的1號傳感器的振動頻譜與模態頻譜有很好的相似性，只是各型振動加速度值和頻率有所差異，這是由于風輪在旋轉時受氣動載荷和離心力的影響所致。因此，本文主要以1號傳感器捕獲的振動頻譜為基礎進行分析，探究翼型凹變對風輪葉片振動特性的影響。

提取不同工況下，A和B葉片的結構振動響應頻譜，并依據模態頻率識別動頻中各階固有振型的位置，如圖10所示(以來流風速為9 m/s，轉速550 r/min為例)。

通過對圖10分析發現，在風輪動態振動頻譜中軸向竄動和旋轉基頻的加速度幅值較高，并且發現在噪聲頻譜和振動頻譜中旋轉基頻的頻率保持良好一致性。因此，本文主要從風輪軸向竄動和旋轉基頻振動幅值進行分析，探究翼型凹變對風輪動頻的影響。

其中，圖10中識別風輪的各階振型如表4所示。

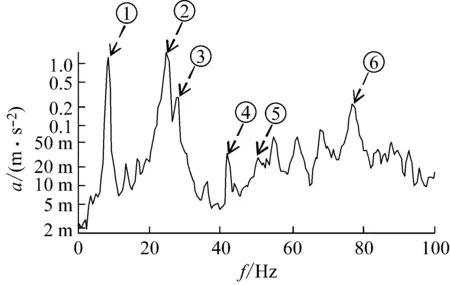
(a) A葉片

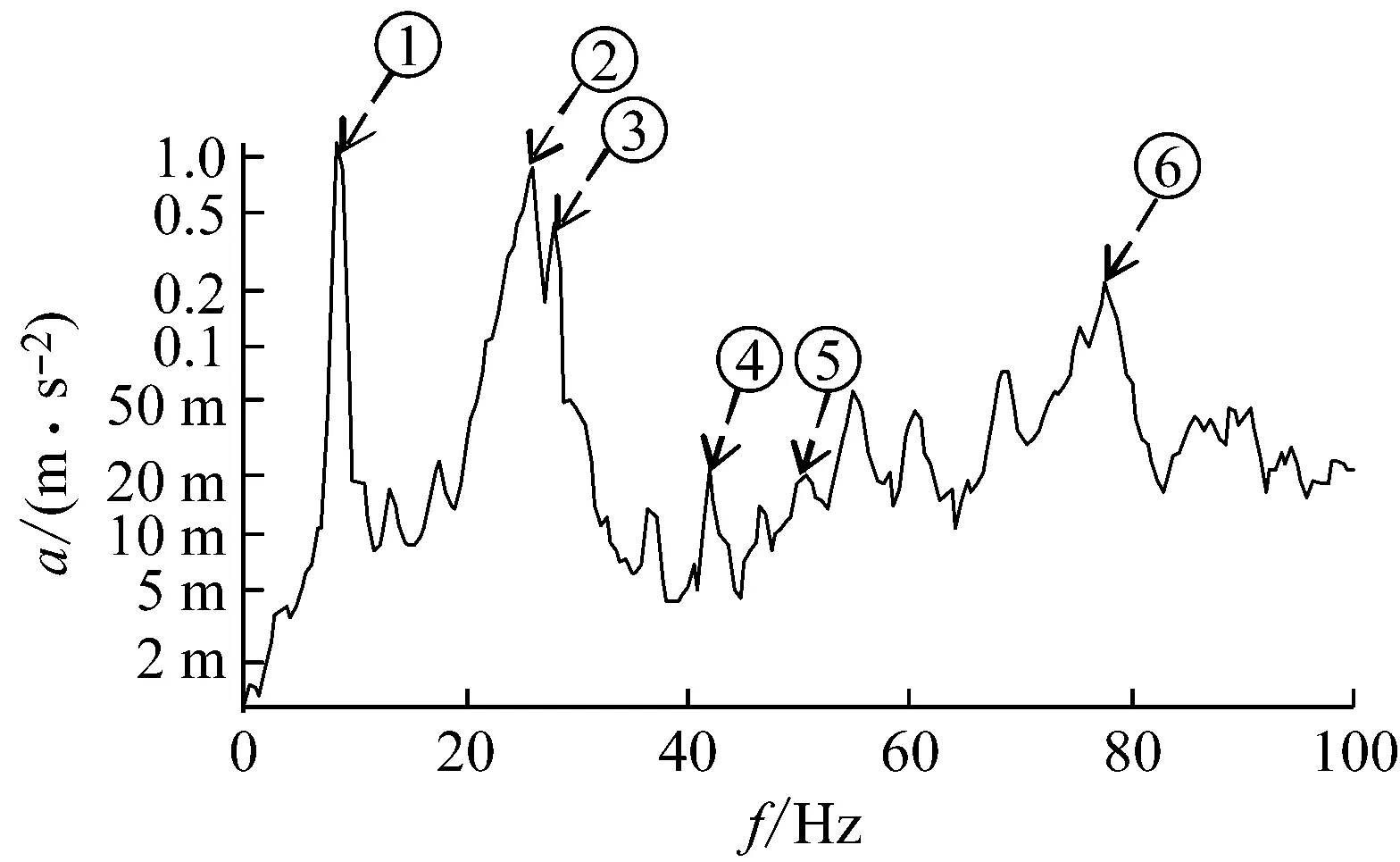
(b) B葉片

表4 振型參照表

2.2.3 對軸向竄動的影響分析

通過對軸向竄動隨工況變化分布圖(圖11)分析發現，在相同工況下B葉片軸向竄動的加速度值普遍小于A葉片，說明翼型凹變后使葉片的動剛度得到提升，在受相同載荷力時可以有效減弱風輪在運行中沿軸向的振動強度。同時，當風速相同時，加速度值隨著轉速的增加呈現出先增加后減小的趨勢，當轉速達到550 r/min時，軸向加速度的值達到最大值。分析原因發現，當轉速為550 r/min時，其旋轉基頻的頻率與風輪一階反對稱的頻率十分接近，導致葉片發生共振，因而導致葉片振動加速度值會出現陡增。隨著風輪轉速的增加，葉片由于離心鋼化作用，其動剛度會進一步增加，進而造成加速度幅值逐漸減小。另外發現，當轉速相同時，軸向竄動的加速度幅值隨著風速的增加而逐漸增大。

2.2.4 對旋轉基頻振動的影響分析

通過對旋轉基頻振動隨工況變化分布圖(圖12)分析發現，在相同工況下B葉片的旋轉基頻加速度幅值普遍小于A葉片，說明翼型凹變也可以有效減弱風輪旋轉基頻的振動強度。同時發現，旋轉基頻加速度的幅值隨工況的變化趨勢與軸向竄動相似，即隨轉速的增加呈現先升高后降低的趨勢，并隨風速的增加而逐漸增大。另外，旋轉基頻的振動加速度幅值要高于軸向竄動，且翼型凹變對旋轉基頻振動的影響較弱。

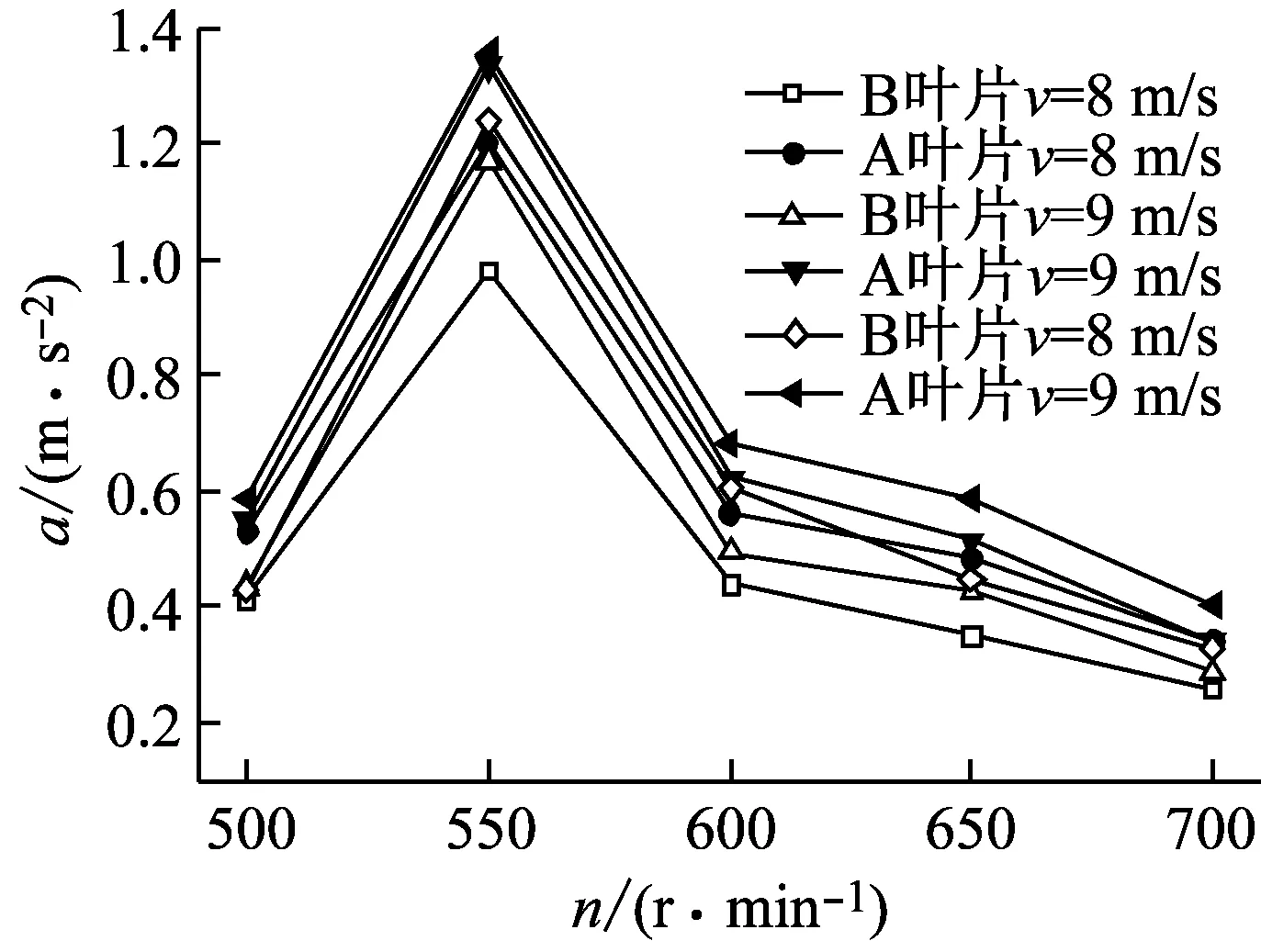
(a) 軸向竄動隨轉速的變化

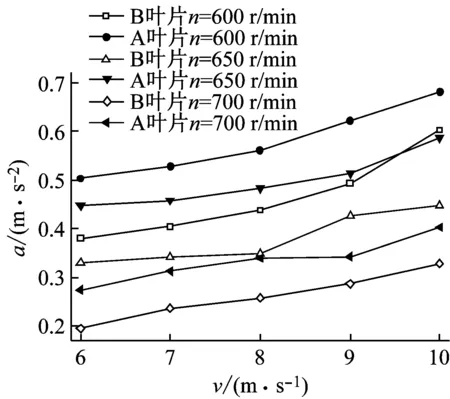
(b) 軸向竄動隨風速的變化

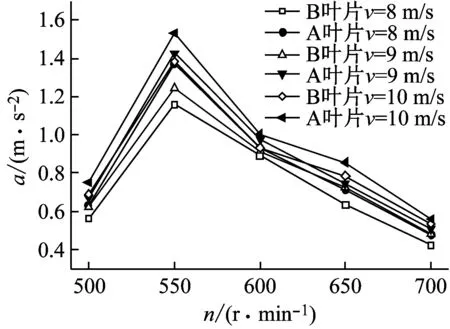
(a) 旋轉基頻振動隨轉速的變化

(b) 旋轉基頻振動隨風速的變化

2.3 關聯性分析

通過對風輪進行模態和動態測試發現，翼型凹變后對葉片剛度的提升，使風輪葉片在受到相同氣動載荷時，風輪的軸向竄動和旋轉基頻振動的振動強度減弱，導致風輪對周圍流體的壓縮和膨脹作用減弱，從而起到降低旋轉噪聲的效果。

另外，通過以上頻譜圖發現葉片的旋轉噪聲和軸向竄動及旋轉基頻振動隨工況的變化趨勢保持良好的相似性。其中當風速相同時，旋轉基頻噪聲的聲壓級隨著轉速呈現出先升高后降低的趨勢，且其峰值出現在轉速為550 r/min的工況，這是因為此刻出現共振現象，導致葉片的振動強度變大，加強了對周圍流體的漲縮作用，從而引起噪聲聲壓級的升高。隨著轉速的升高，葉片受離心鋼化作用，進一步提升了葉片的剛度，從而逐步減弱了對周圍流體的漲縮作用，導致聲壓級隨轉速的升高而逐漸降低。

3 結 論

本文主要對風輪葉片進行旋轉噪聲、模態和動頻測試，探究了翼型凹變對風輪旋轉噪聲和結構特性的影響，同時，分析了風輪旋轉噪聲產生的原因以及葉片振動與噪聲之間的關聯性，并得出以下結論。

通過對葉片軸向竄動和旋轉基頻振動分析發現，在相同工況下，翼型凹變后對葉片剛度的提升，可以有效減弱葉片的振動強度。

通過對風輪旋轉噪聲分析發現，在相同工況下，翼型凹變后可以明顯降低風輪的旋轉噪聲，且降噪效果隨著旋轉基頻的倍頻次數增加而逐漸增強。

通過對風輪旋轉噪聲產生原因分析發現，翼型凹變后對葉片剛度的提升，使風輪葉片在受到相同氣動載荷時，風輪的振動強度減弱，導致風輪對周圍流體的壓縮和膨脹作用減弱，從而起到降低旋轉噪聲的效果。