考慮場地土參數隨機性和相關性的地震動降維模擬

劉章軍， 鄭麗慧， 阮鑫鑫

(1. 三峽大學 土木與建筑學院， 湖北 宜昌 443002； 2. 武漢工程大學 土木工程與建筑學院， 武漢 430074)

大量強震觀測記錄和震害資料表明，場地條件對地震波的傳播有較大的影響，它表現為對地震動的不同頻率成分有很強的放大或縮小作用，并直接影響到地震災害程度的分布[1]。場地條件對震害的影響實際上是由于場地條件對地震動的影響所致，該影響主要表現在對地震動幅值和地震動頻譜特性的變化上[2]。隨著人們不斷的深入研究，現已有諸多關于場地條件對地震動影響的研究成果[3-7]。同時國內外抗震設計規范、地震區劃中也不同程度的考慮了場地條件對地震動參數的影響[8-10]。世界各國的抗震規范普遍是以場地的剪切波速為依據進行場地類別劃分，不同場地類別給出相應的設計地震反應譜。我國現行規范《建筑抗震設計規范》(GB 50011—2010)考慮了場地條件對反應譜特征周期的影響，《中國地震動參數區劃圖》(GB 18306—2015)同時考慮了場地條件對地震動峰值加速度和反應譜特征周期的影響。

在地震工程抗震設計中，合理地確定地震動輸入，是進行結構隨機地震反應分析與抗震可靠度計算的重要基礎。由于強震記錄的數量有限以及對具體地震環境和場地條件的限制,現有強震動記錄難以滿足工程結構抗震分析的需求[11]。隨著人工模擬隨機過程技術的發展，采用隨機地震動模型進行模擬獲得地震動時程的樣本集合是地震動輸入領域研究的熱點。現階段，一般依據抗震規范中的基本參數(如地震烈度和場地類別或震級、震中距和場地類別)對應給出隨機地震動模型的參數取值(如地震動峰值、持時和場地土的卓越頻率和阻尼比等)。但是同一類別場地的地震動特性具有較大的離散性，不同類別場地的地震動特性還常出現交叉，且依據抗震規范給出的隨機地震動模型參數取值均為確定性值，只是對場地條件的粗略考慮，無法反映場地條件的隨機性。因此，針對場地條件和場地土參數的變異性對地震動影響的研究也開展了許多工作[12-15]。郭婷婷等[12-14]研究了土層參數的隨機性對場地地震動參數(加速度峰值與反應譜)的影響。丁艷瓊等[15]為克服隨機地震動模型的局限性，提出了工程隨機地震動的物理模型，在該模型中考慮了局部場地條件對地震動的影響，并假定場地土隨機參數是相互獨立的。

基于上述研究進展，為了進一步探討場地條件的隨機性以及場地土參數的相關性對地震動的影響，本文在非平穩地震動過程的演變功率譜模型[16]基礎上，考慮場地土參數的隨機性以及場地土參數之間的相關性，根據非確定性譜幅值(NSA)模擬方法[17-18]，引入隨機函數的降維思想[19]，實現非平穩地震動過程的降維模擬，得到非平穩地震動加速度的代表性時程集合。同時，通過數值算例分析與實測強震動記錄驗證了模擬方法的有效性和工程適用性。

1 非平穩地震動過程的演變功率譜模型

根據非平穩隨機過程的Priestley演變譜理論，非平穩地震動加速度過程的演變功率譜密度函數[20]

(1)

式中：SUg(t,ω)為非平穩地震動加速度過程Ug(t)的雙邊演變功率譜密度函數；S(ω)為相應平穩地震動加速度過程的雙邊功率譜密度函數；A(t,ω)為時-頻調制函數。

對于平穩地震動加速度過程的功率譜密度函數，采用Clough-Penzien譜[21]

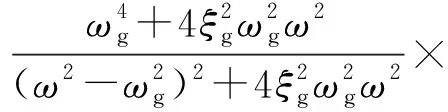
(2)

式中:ωg和ξg分別為場地土的卓越圓頻率和阻尼比；ωf和ξf分別為基巖的卓越圓頻率和阻尼比；S0為地震動的譜強度因子，可定義為[22]

(3)

式中：amax為地震動峰值加速度(PGA)；r為峰值因子。根據文獻[11]，非平穩地震動過程的演變功率譜參數取值如表1。

對于非平穩地震動的時-頻調制函數A(t,ω)，采用如下形式的調制函數

A(t,ω)=

ω>0

(4)

其中

(5)

在時-頻調制函數式(4)中，共有3個參數a，b和c。為了確定3個參數的取值，建議b=a+0.001，c=0.005，其中參數a取值如表1。

在非平穩地震動加速度過程的演變功率譜SUg(t,ω)中，參數ωg和ξg反映了場地土特性。場地土參數ωg、ξg具有較強的隨機性，本文將它們視為隨機變量。

對于基巖參數ωf和ξf，本文將它們均視為一個確定性量，可定義如下

ωf=0.1×E[ωg]=0.1μ1

(6a)

ξf=E[ξg]=μ2

(6b)

式中，E[·]為數學期望，其中場地土隨機參數ωg和ξg的均值如表1所示。

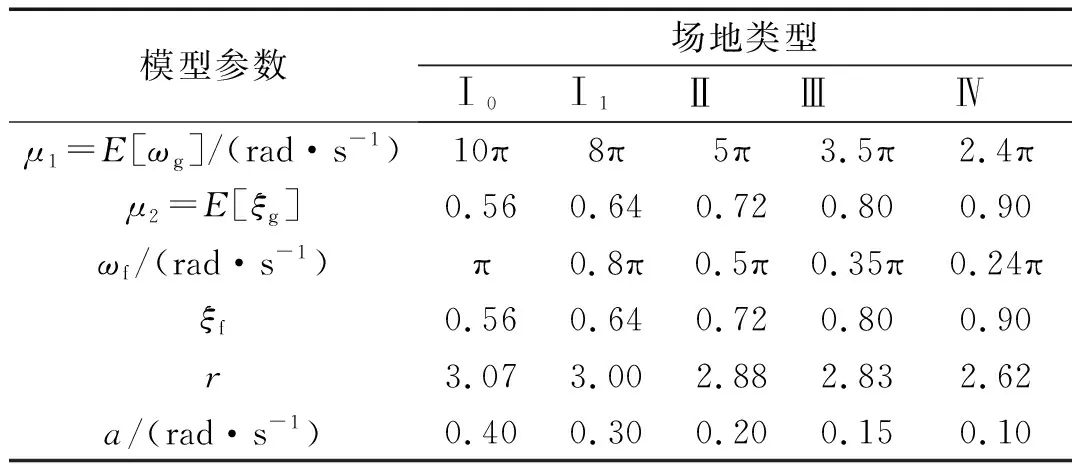
表1 非平穩地震動演變功率譜模型的參數取值

2 場地土參數的隨機函數表達

考慮到局部場地土參數的隨機性對地震動時程有重要影響，在非平穩地震動過程的演變功率譜模型中，選取場地土的卓越圓頻率ωg和阻尼比ξg作為隨機參數。為此，可將場地土的隨機參數ωg和ξg分別定義為

ωg=μ1(1+δ1α)

(7a)

ξg=μ2(1+δ2β)

(7b)

式中：μ1和δ1分別為隨機參數ωg的均值和變異系數；μ2和δ2分別為隨機參數ξg的均值和變異系數；α和β分別表示均值為零，方差為1的標準化隨機變量。

同時，為了充分考慮場地土隨機參數ωg和ξg之間的相關性，進一步地將隨機變量α和β分別定義為兩個相互獨立的基本隨機變量Θ1和Θ2的函數形式

α=Θ1sinφ+Θ2cosφ

(8a)

β=Θ1cosφ+Θ2sinφ

(8b)

式中：φ為區間[0,2π)上任一確定性值；Θ1和Θ2是均值為零，標準差為1的相互獨立的基本隨機變量。

將式(8)代入式(7)中，即可得到場地土參數ωg和ξg的隨機函數表達式

ωg=μ1[1+(Θ1sinφ+Θ2cosφ)δ1]

(9a)

ξg=μ2[1+(Θ1cosφ+Θ2sinφ)δ2]

(9b)

于是，場地土隨機參數ωg和ξg的相關系數ρωgξg表達式為

(10)

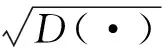
在本文中，假定基本隨機變量Θ1和Θ2均服從標準正態分布，并注意到Θ1和Θ2相互獨立，根據式(9)可知，場地土隨機參數ωg和ξg也都服從正態分布。同時，根據我國現行《建筑抗震設計規范》(GB 50011—2010)中關于場地類別的分類及其特征周期的取值，卓越圓頻率ωg從場地類別I0到場地類別Ⅳ是逐漸減小的，而阻尼比ξg從場地類別I0到場地類別Ⅳ則是逐漸增大的。因此，可以認為場地土隨機參數ωg和ξg之間是負相關的，即相關系數ρωgξg的取值應當在[-1,0]范圍內。

總之，對于場地土隨機參數ωg和ξg，本文只需給出均值、變異系數及相關系數等數字特征即可確定它們的概率分布及其相關性，這為工程應用提供了方便。

3 非平穩地震動過程的降維模擬

在非平穩地震動過程的演變功率譜理論基礎上，文獻[19]建議了一類實非平穩地震動過程模擬的源譜表達

Ug(t)=

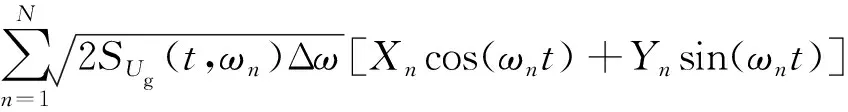
(11)

式中：Ug(t)為非平穩地震動加速度的模擬過程；Δω為頻率步長，ωn=nΔω；N為頻率截斷項數。

E[Xn]=E[Yn]=0,E[XmYn]=0

(12a)

E[XmXn]=E[YmYn]=δmn

(12b)

式中，δmn表示Kronecker符號。

由于式(12)中標準正交隨機變量Xn和Yn的概率分布未給定，因而不能直接用于模擬。為此，根據文獻[17-18]提出的兩種譜表示方法，即確定性譜幅值(DSA)方法與非確定性譜幅值(NSA)方法。在確定性譜幅值(DSA)方法中，幅值是由功率譜密度函數來確定的，而非確定性譜幅值(NSA)方法中的幅值卻具有隨機性。考慮到地震動峰值加速度本身具有隨機性，本文應用非確定性譜幅值(NSA)方法，同時引入隨機函數的思想[19]，實現非平穩地震動過程的降維模擬。

3.1 傳統的非確定性譜幅值(NSA)模擬方法

Xn=Ancosφn,Yn=Ansinφn

(13)

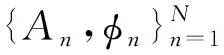
將式(13)代入式(11)，得到傳統的非確定性譜幅值模擬方法

(14)

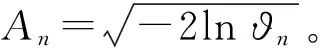
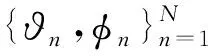
因此，式(14)也可以表示為

(16)

式(14)和式(16)統稱為傳統的非確定性譜幅值(NSA)模擬方法。

3.2 基于非確定性譜幅值(NSA)的降維模擬

傳統的非確定性譜幅值(NSA)模擬方法往往需要高達上千個隨機變量才能保證所需的精度，從而極大地增加了復雜結構非線性隨機地震反應分析的難度。因此，利用隨機函數的降維思想，將源譜表達式(11)中的標準正交隨機變量定義為2個基本隨機變量的正交函數形式，從而實現非平穩地震動過程模擬的高效降維。

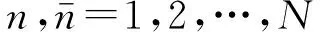
(17)

式中：基本隨機變量Θ3和Θ4相互獨立，且都服從區間[0,2π)上的均勻分布；α是區間[0,2π)上的確定性常數，本文取α=π/4。

將式(17)代入式(11)中，得到非平穩地震動過程的降維模擬

Ug(t)=

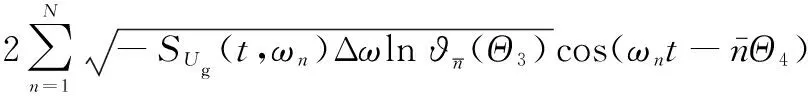
(18)

其中

(19)

式中：基本隨機變量Θ3反映了地震動幅值的隨機性；Θ4則反映了地震動相位的隨機性。

總之，在非平穩地震動過程的降維模型中，共有4個基本隨機變量Θ1、Θ2、Θ3和Θ4，其中Θ1和Θ2表征場地土參數的隨機性，Θ3表征地震動幅值的隨機性，Θ4表征地震動相位的隨機性。由于Θ1和Θ2是相互獨立的，因此可以認為4個基本隨機變量Θ1、Θ2、Θ3和Θ4是相互獨立的。這樣，僅需4個相互獨立的基本隨機變量即可模擬非平穩地震動加速度過程，從而克服Monte Carlo模擬方法需要上千個隨機變量的局限性，為復雜工程結構的隨機地震反應分析和抗震可靠度計算奠定了基礎。

4 數值算例

4.1 降維模擬的實現

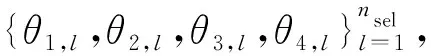
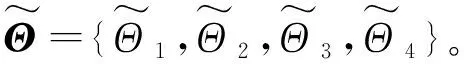
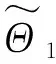
(20)

式中，Φ(·)為標準正態隨機變量Θi(i=1,2)的分布函數。于是，對式(20)進行逆變換得到

(21)

式中，Φ-1(·)為標準正態分布函數Φ(·)的反函數。

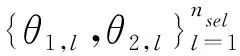
θi,l=Φ-1(?i,l)，i=1,2；l=1,2,…,nsel

(22)

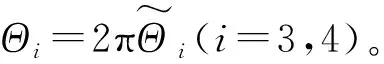
θi,l=2π?i,l，i=3,4；l=1,2,…,nsel

(23)

于是，將基本隨機變量Θ1和Θ2的代表性點{θ1,l,θ2,l}(l=1,2,…,nsel)依次代入式(9)中，得到nsel組場地土隨機參數ωg和ξg的代表性取值。同時，也將基本隨機變量Θ3和Θ4的代表性點{θ3,l,θ4,l}(l=1,2,…,nsel)依次代入式(18)中，即可得到nsel條非平穩地震動加速度過程的代表性時程。顯然，每條代表性時程都具有給定的賦得概率Pl(l=1,2,…,nsel)，且所有nsel條代表性時程構成一個完備的概率集合。

4.2 結果分析

本文僅考慮地震烈度為8度，設計基本地震動加速度PGA=0.2g，地震動加速度過程降維模擬的參數取值為：頻率截斷項數N=1 600，頻率步長Δω=0.15 rad/s，截斷頻率ωu=240 rad/s；地震動持時T=40 s；時間步長Δt=0.01 s；地震動峰值加速度amax=200 cm/s2；代表性時程的數量nsel=307。同時，為了考慮場地土隨機參數ωg和ξg的相關性對地震動時程的影響，表2給出了相關系數ρωgξg的三種不同情況，以及場地土隨機參數ωg和ξg的變異系數。

表2 場地土隨機參數ωg和ξg的取值

圖1給出了場地類別Ⅰ1條件下的隨機參數ωg和ξg的概率分布。從圖1中可見，隨機參數ωg和ξg的代表性離散值的直方圖分布與目標的正態分布擬合很好，表明本文所采用的數論方法以及反變換方法生成基本隨機向量的代表性點集是十分有效的。

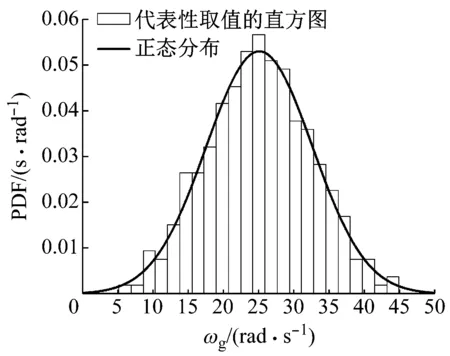
(a) 隨機參數ωg

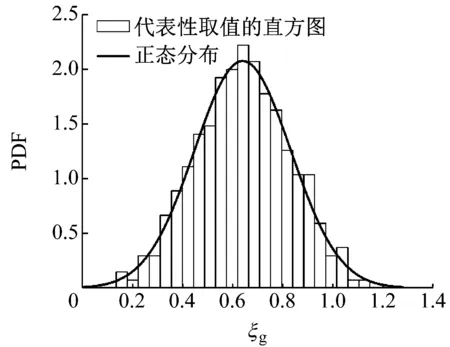
(b) 隨機參數ξg

圖2分別給出了場地類別Ⅰ1和Ⅲ條件下的3種不同相關系數時，降維模擬方法所生成的地震動代表性時程。從圖2中可見，同一場地類別的同一條代表性時程隨相關系數ρωgξg的取值不同，代表性時程的頻率成分差異明顯。因此，場地土隨機參數ωg和ξg的相關性對地震動代表性時程的影響較大，隨著隨機參數ωg和ξg線性相關的程度較好時，即|ρωgξg|值越大時，地震動加速度代表性時程的高頻成分更加豐富。

(a) 場地類別Ⅰ1

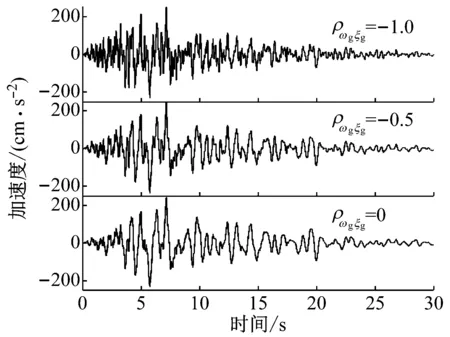
(b) 場地類別Ⅲ

圖3分別給出了相關系數ρωgξg=-0.5時場地類別Ⅰ1和Ⅲ條件下的地震動代表性時程。從圖3中可見，同一場地類別所生成的地震動加速度代表性時程，在強度和頻率非平穩特性以及地震波形等方面表現出明顯的差異，且不同場地類別的地震動加速度代表性時程在頻譜成分、波形、持時等方面均表現出明顯的差異。

圖4分別給出了場地類別Ⅰ1和Ⅲ條件下的相關系數ρωgξg=-0.5時，降維模擬方法所生成的地震動加速度代表性時程集合的均值及標準差與目標值的比較。從圖4中可見，地震動加速度代表性時程集合的均值及標準差在目標值的上下微小波動，兩者的擬合程度較好。

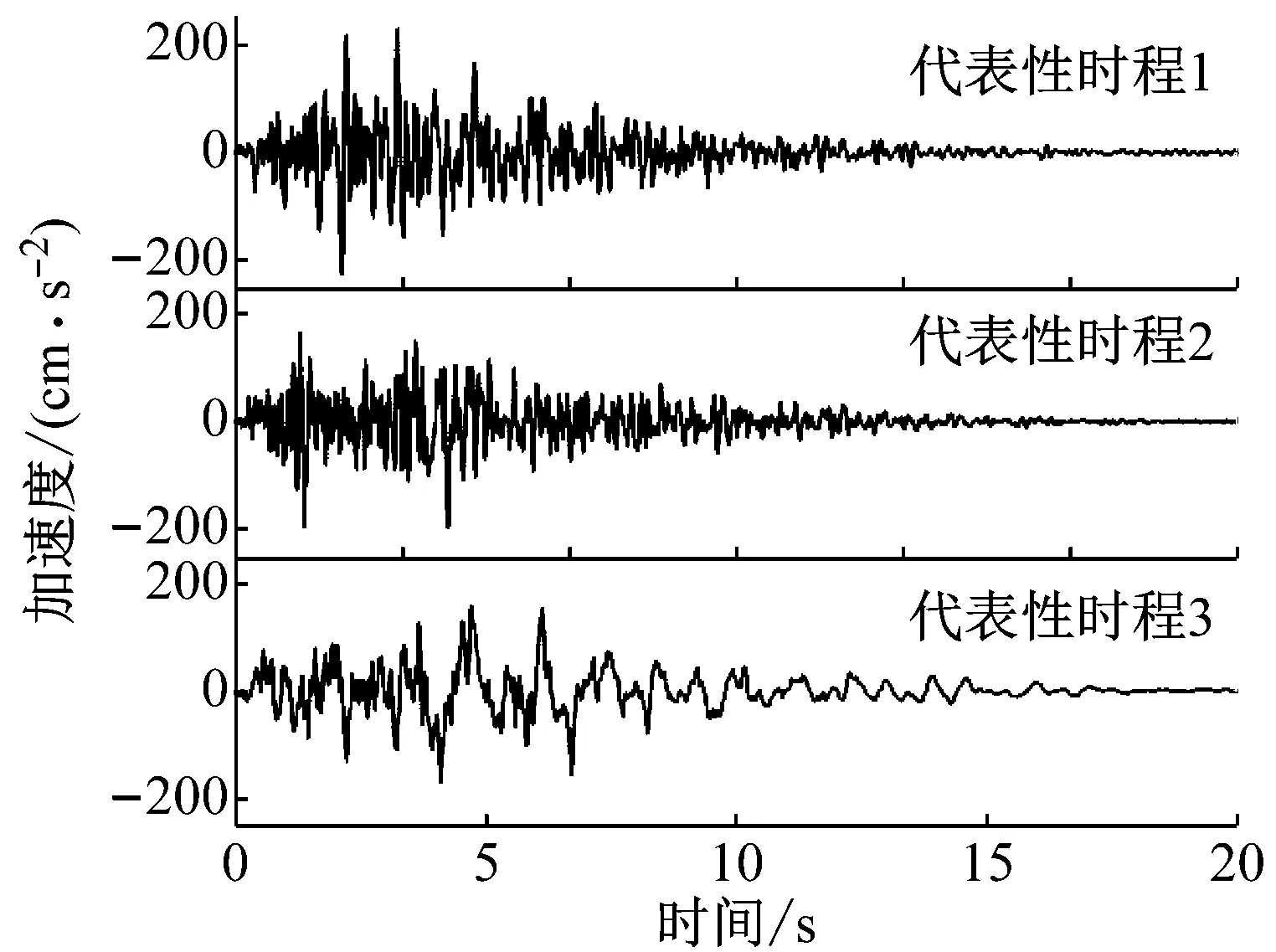
(a) 場地類別Ⅰ1

(b) 場地類別Ⅲ

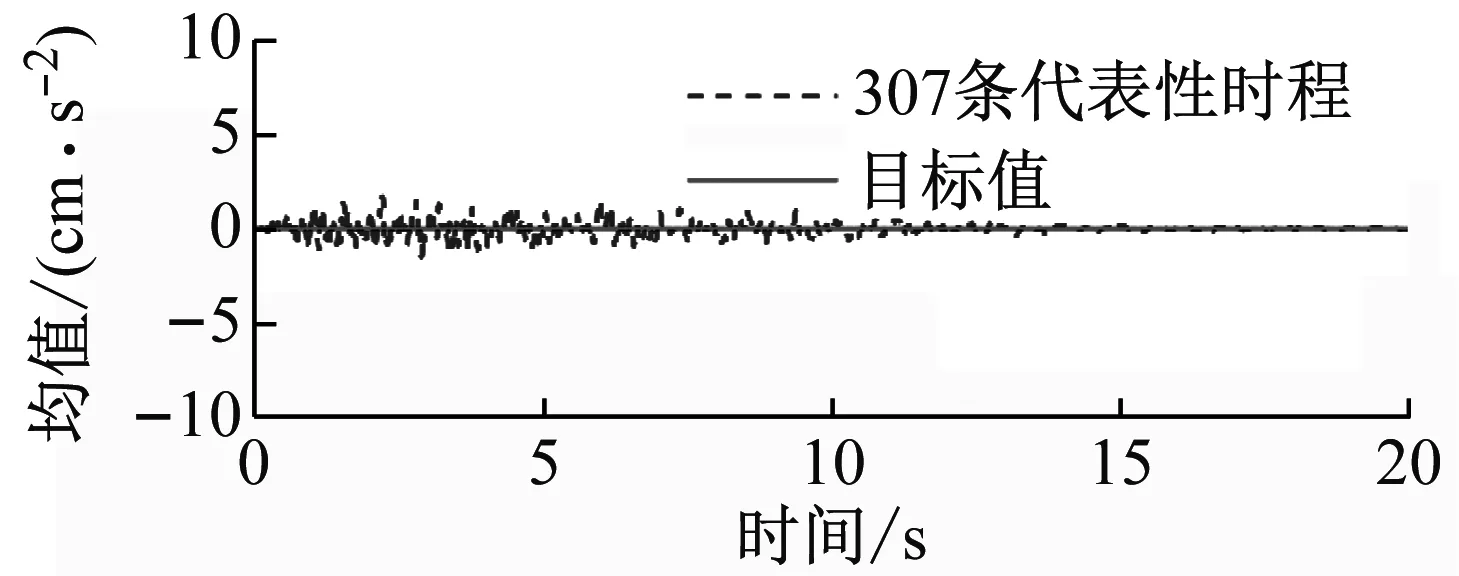
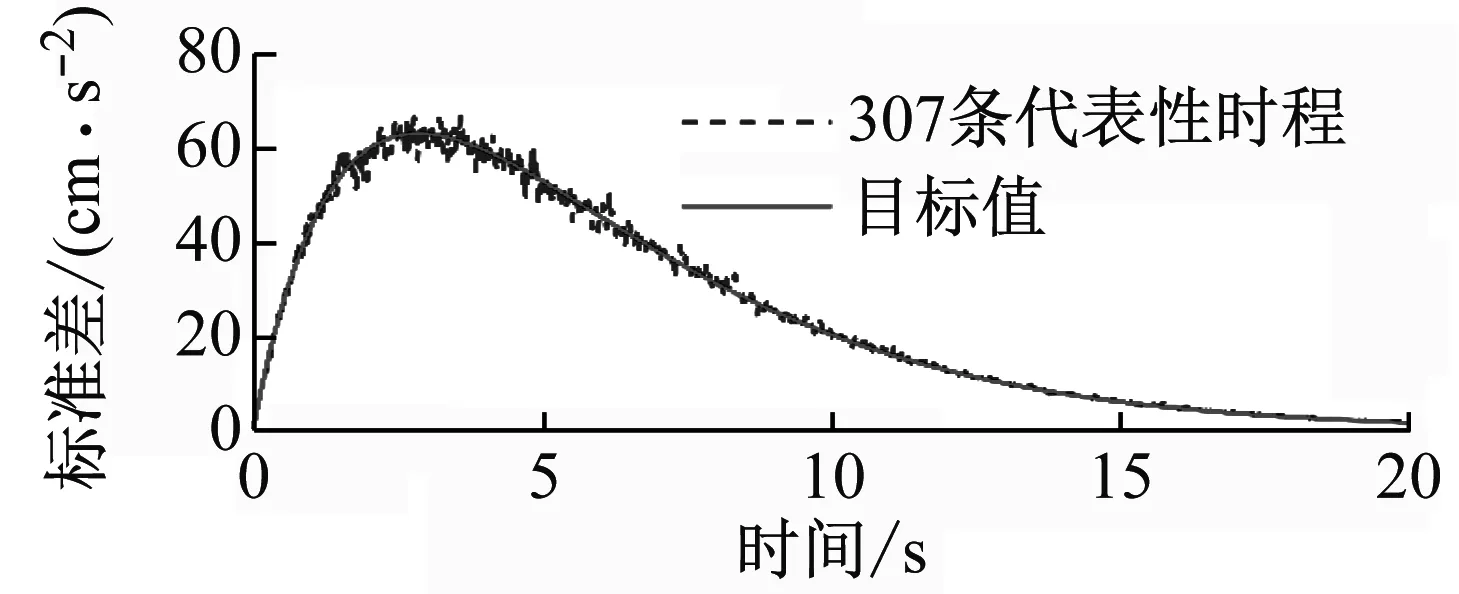
(a) 場地類別Ⅰ1

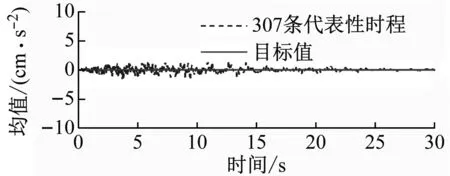
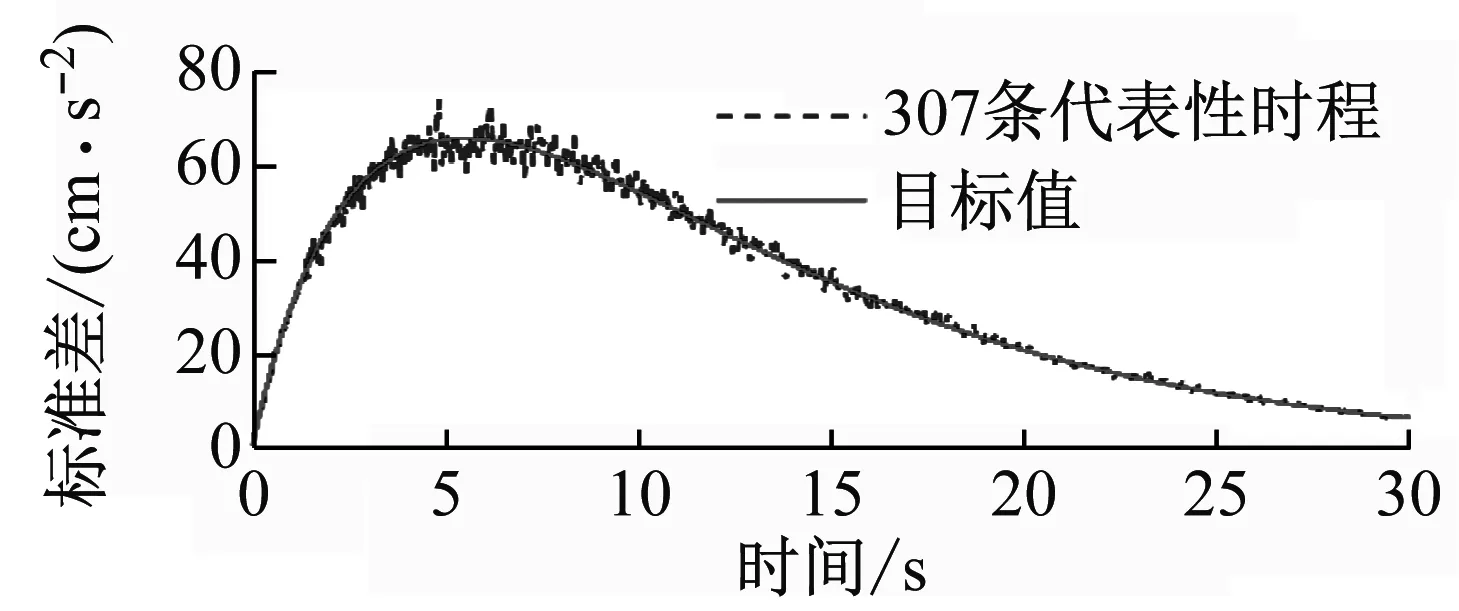
(b) 場地類別Ⅲ

進一步，表3給出了地震動加速度代表性時程集合的均值及標準差的相對誤差。從表3中可見，場地土隨機參數ωg和ξg的相關性對均值的相對誤差有一定的影響，而對標準差的相對誤差的影響很小。同時，地震動加速度代表性時程集合的均值和標準差的相對誤差均小于5%，表明所有場地類別的代表性時程集合的模擬結果均與目標值擬合較好。

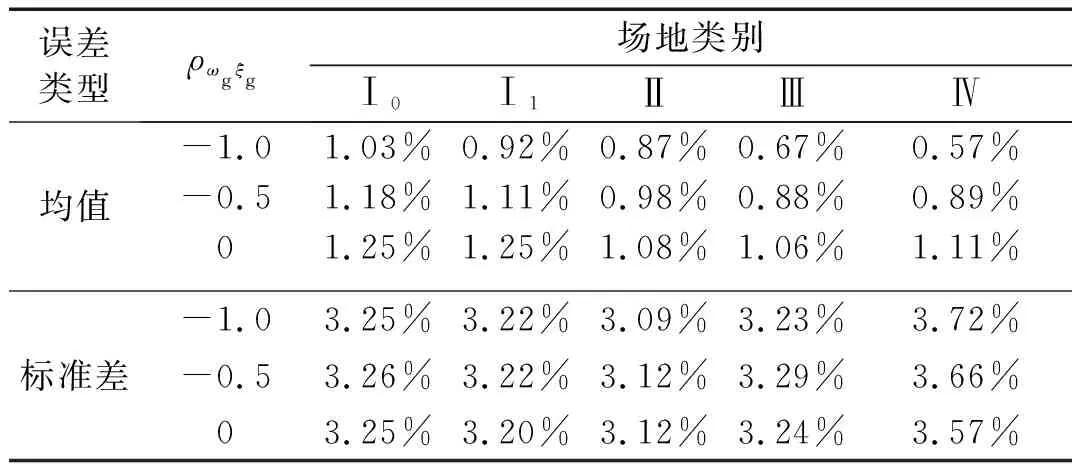
表3 模擬非平穩地震動過程的均值和標準差的相對誤差

5 基于實測強震動記錄的驗證

為了進一步說明本文方法的有效性，將模擬的非平穩地震動代表性時程與實測強震動記錄進行比較。采用文獻[11]中選取的來自中國以及世界其他地區的共計61次地震中記錄到的920條水平地震動。同時，文獻[11]根據《中國地震動參數區劃圖》中規定的場地類別Ⅰ0、Ⅰ1、Ⅱ、Ⅲ及Ⅳ，給出了Vs30(地表以下30 m范圍內的平均剪切波速)的取值范圍與5類場地類別之間的對應關系，以及對應于不同場地類別的強震動記錄數量。為了進行比較，計算了所選920條強震動記錄的加速度反應譜和Fourier幅值譜。考慮到強震動記錄的噪聲影響，根據信噪比可取Fourier幅值譜的有效頻率范圍為0.2～30 Hz。

圖5分別給出了實測強震動記錄的加速度反應譜及加速度Fourier幅值譜與本文方法模擬結果的比較。為簡便起見，圖5僅給出了相關系數ρωgξg=-0.5情況下Ⅰ1和Ⅲ類場地的結果。事實上，所有場地類別的實測強震動記錄均在模擬均值的1倍標準差范圍內，且與模擬均值的擬合較為一致。這表明，本文方法模擬的地震動加速度過程具有良好的工程適用性。

6 結 論

本文在非平穩地震動過程的演變功率譜模型基礎上，建議了一種能夠考慮場地土參數隨機性和相關性的隨機函數表達。同時，應用非確定性譜幅值(NSA)方法，引入隨機函數的降維思想，模擬非平穩地震動隨機過程，生成地震動加速度過程的代表性時程集合。本文方法的優點在于，既考慮了場地土參數的隨機性對地震動時程的影響，又考慮了場地土參數之間的不同相關系數對地震動時程的影響。數值算例分析與實測強震動記錄驗證了本文方法的有效性和工程適用性，得出以下結論：

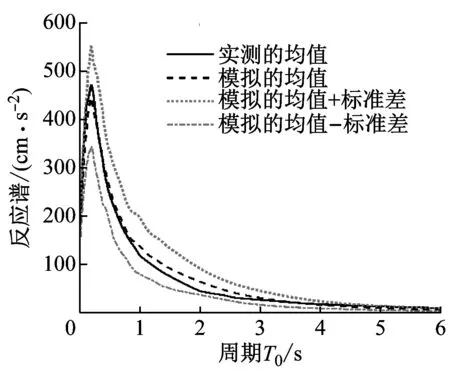
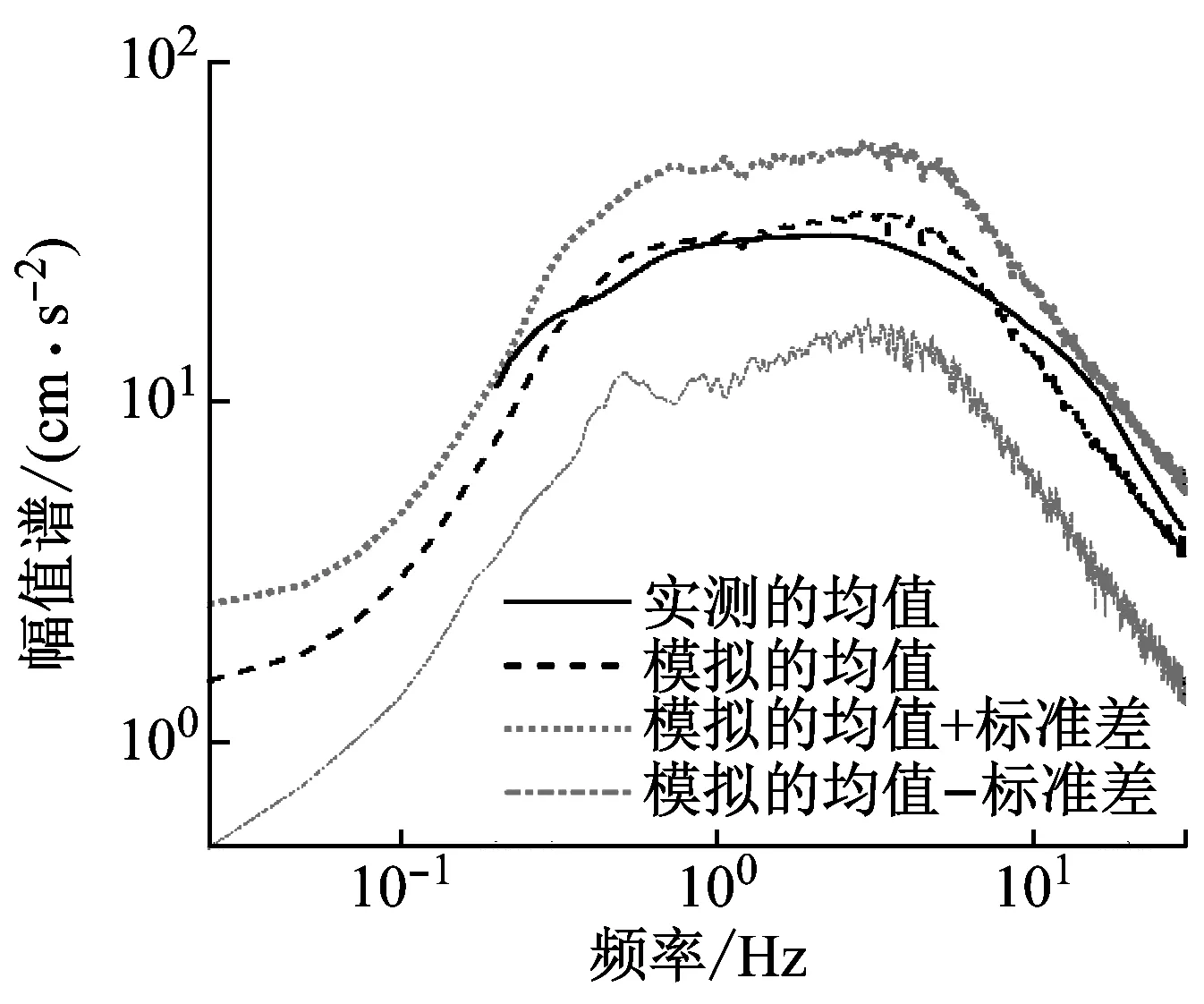
(a) 場地類別Ⅰ1

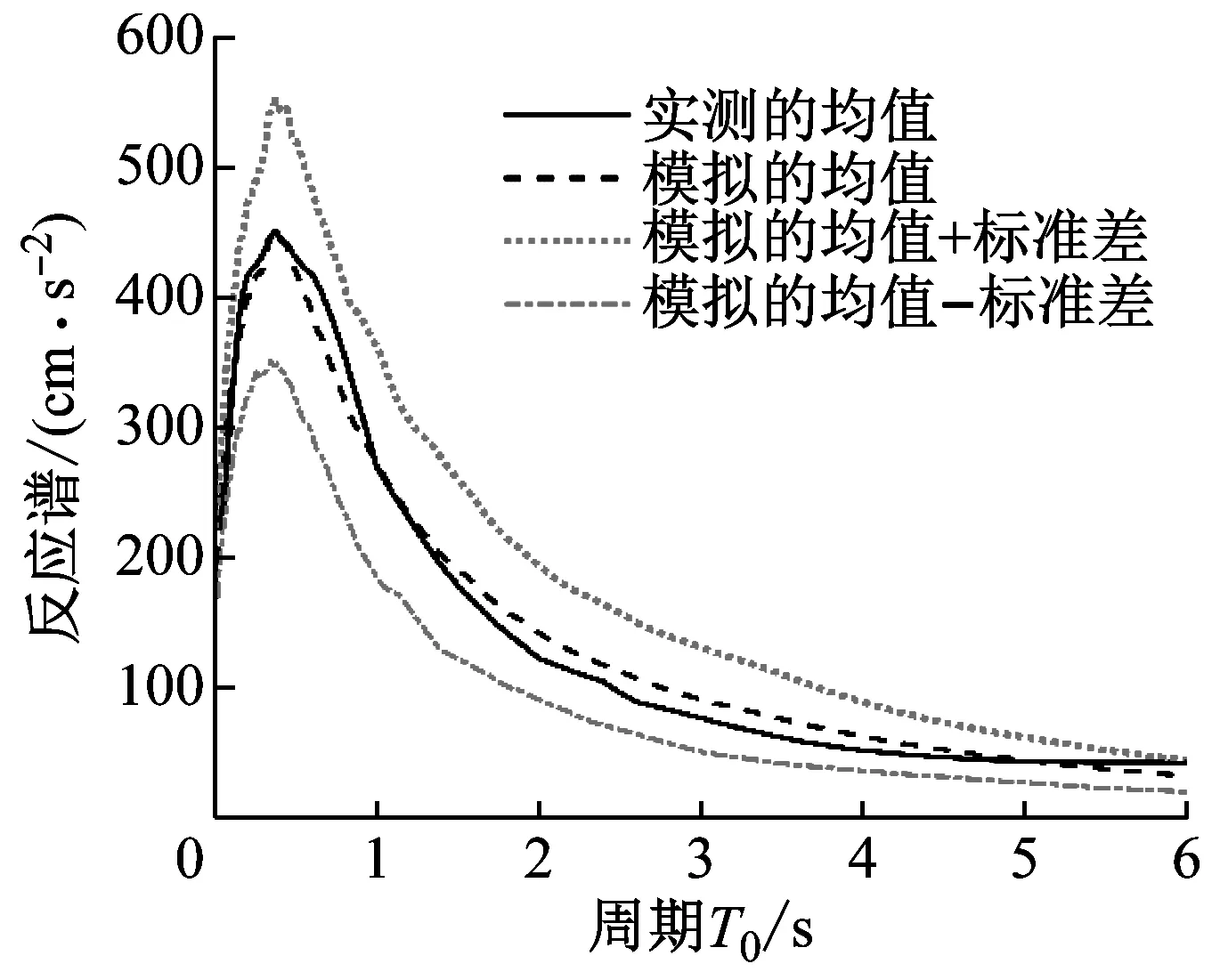
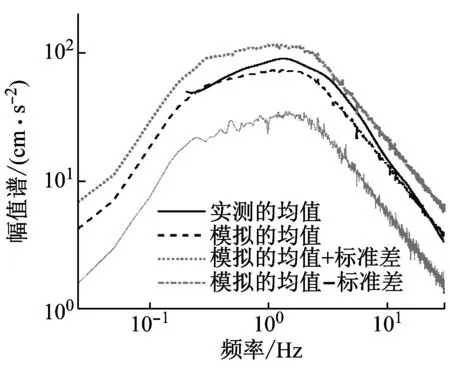
(b) 場地類別Ⅲ

(1) 考慮場地土參數的隨機性，通過構造場地土參數的隨機函數形式，實現只需4個基本隨機變量即可對地震動加速度過程進行降維模擬。對于同一場地類型所生成的地震動加速度代表性時程，在強度非平穩和頻率非平穩特性以及地震波形等方面表現出明顯的差異，能夠直接反映地震動顯著的隨機性和非平穩性。

(2) 考慮場地土參數之間的相關性，通過考慮場地土參數的3種不同相關系數所生成的地震動代表性時程，可以發現場地土參數的相關性對地震動代表性時程的頻率成分影響較大，即隨著場地土隨機參數ωg和ξg線性相關的程度較好時，地震動加速度代表性時程的高頻成分更加豐富。

(3) 基于NSA的降維模擬方法生成的地震動加速度過程的代表性時程的平均值和標準差與目標值吻合較好。采用數論方法以及反變換方法生成基本隨機向量的代表性點集是十分有效的，進而生成的每一條代表性時程都具有相應的賦得概率，且所有的代表性時程并構成一個完備的概率集，這為應用概率密度演化理論進行復雜工程結構的隨機地震反應分析及抗震可靠度精細化計算提供了基礎。