生態學區組試驗設計的方差分析及P值探討

呂世杰，閆寶龍,2，王忠武，李治國*，，康薩如拉，劉紅梅

(1.內蒙古農業大學草原與資源環境學院/草地資源教育部重點實驗室/農業農村部飼草 栽培、加工與高效利用重點實驗室/內蒙古自治區草地管理與利用重點實驗室，呼和浩特 010019; 2.內蒙古民族大學農學院，通遼028043；3.內蒙古自治區林業科學研究院，呼和浩特 010010)

在生態學野外或田間試驗中，我們常用到區組試驗設計[1～3],原因是區組試驗設計操作相對簡單，數據分析相對容易掌握，研究者更愿意接受并用于揭示研究對象的變化特征和變化規律[4～6]。然而,事實上試驗設計的操作簡單不等于數據分析的科學運用。盡管有什么樣的試驗設計就會有什么樣的數據分析方法，但數據分析方法受試驗設計種類、樣本容量、取樣方法和模型參數等多方面的影響[4,5,7]。區組試驗設計的數據分析方法首先考慮到的就是方差分析[4,5]。然而，方差分析模型的選取并不是單因素和雙因素這么簡單，也不是固定模型和隨機模型這么容易，而是一個綜合考量過程[5,6]。方差分析結果判斷出顯著差異之后，需要進一步做多重比較[5,6]。可是，我們在文獻中經常會看到多重比較結果等同于方差分析[1～3]。因此，方差分析模型選取以及其與多重比較的關系有必要詳細闡明。特別值得注意的是，近些年對于P值問題的爭論引起了統計學界高度重視，對其他學科的影響也具有深遠的意義[8～10]。本研究立足于生態學單因素區組試驗設計，采用實例解析的方法對方差分析模型選取、多重比較、差異顯著性(P值)逐一探討，為生態學區組試驗設計的數據分析提供科學合理的解決途徑，也為生態學科學問題的闡釋給予比較全面的理論支撐。

1 材料和方法

試驗數據來源于內蒙古農業大學草原與資源環境學院四子王旗放牧試驗基地，放牧試驗基地采用區組試驗設計[11]。2016年8月份，在每一個試驗處理區隨機選擇10個50cm×50cm的樣方，測定短花針茅植物種群的高度、蓋度、密度和地上現存量以及植物群落地上現存量，并以該試驗設計下的取樣數據(高度、密度)展開方差分析相關問題的討論。數據分析采用SAS 9.2軟件，其中正態性檢驗調用UNIVARIATE過程，方差分析調用GLM過程，多重比較選用DUNCAN關鍵字，方差同質性選用HOVTEST關鍵字。

2 方差分析相關問題探討

2.1 樣本容量如何確定

從表1看出，每一載畜率下樣本容量為27或30個觀測數據，這一樣本指的是觀測樣本容量，而不是試驗設計樣本容量。試驗設計的樣本容量由4個載畜率和3個區組構成，也就是總樣本容量為12個數據。這一點可以從單因素區組試驗設計的模型[4]中可以看到：

xij=μ+αi+βj+εij

(1)

式中，xij為觀測數據(每一載畜率每一區組內短花針茅種群高度或密度)；μ為總體(短花針茅種群高度或密度)均值；αi為載畜率導致短花針茅種群高度或密度的差異；βj為區組試驗設計中區組導致短花針茅種群高度或密度的差異。因此，每一載畜率每一區組內10個觀測樣方的觀測數據不能直接用于方差分析，原因是違背了單因素區組試驗設計數據分析的統計模型。那么每一載畜率每一區組內短花針茅種群高度或密度觀測數據(表1中7或10個樣本容量)還有沒有意義，原因是生態學野外或田間試驗空間異質性大，觀測數據波動性大，需要增加觀測重復來彌補數據的波動性，從而使獲得的觀測數據均值更穩定，更具有代表每一載畜率每一區組內短花針茅植物種群高度或密度指標的集中情況。

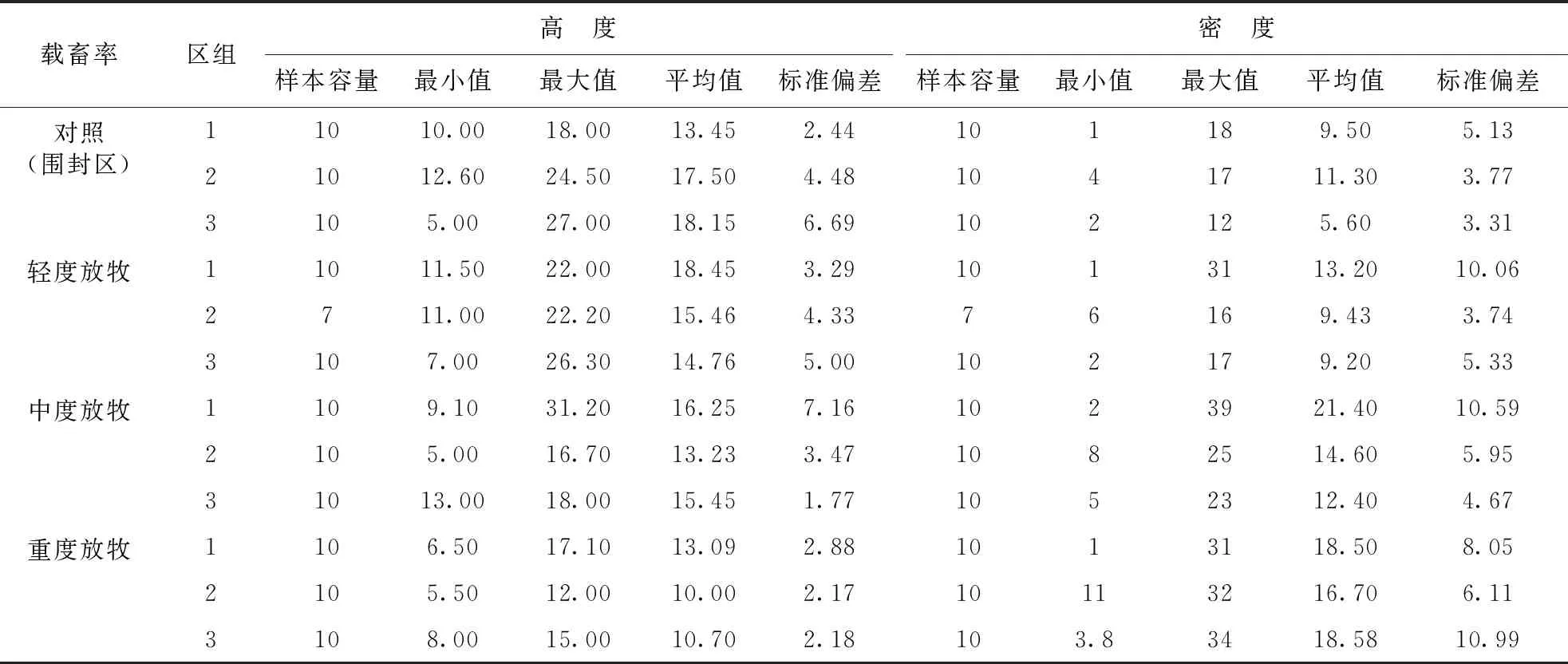
表1 不同載畜率下短花針茅植物種群高度和密度樣本數據描述

2.2 正態性檢驗

確定了樣本對象和樣本容量，我們才能進入正態性檢驗環節，這是方差分析的前提條件之一。在荒漠草原，短花針茅高度屬于數量性狀數據(連續型變量)，而密度屬于質量性狀數據(非連續性變量)，所以有必要先假設荒漠草原短花針茅這一總體的高度、密度服從正態分布[5]。短花針茅高度、密度數據的樣本容量均為12個，高度經Shapiro-wilk檢驗[4,6]統計量W=0.9524，P=0.6730；Kolmogorov-smirnov檢驗[4,6]結果顯示，D=0.1098，P>0.1500；所以高度屬于正態分布數據。密度經Shapiro-wilk檢驗統計量W=0.9679，P=0.8872；Kolmogorov-smirnov檢驗結果顯示，D=0.1275，P>0.1500；所以密度也屬于正態分布數據。因此，高度和密度指標可以進行下一步數據分析過程。

2.3 方差同質性檢驗

方差同質性檢驗調用SAS的GLM過程，一般在MEANS關鍵字后的待比較變量進行指定，格式為“MEANS CHL/HOVTEST DUNCAN ALPHA=0.05”，其中CHL代表載畜率變量，其余屬于SAS系統關鍵字[12]。在這里需要明白一點，當進行多重比較時不管因素變量存在幾個，只是針對其中的一個因素變量進行比較，其余因素變量均變為重復。所以，多因素變量的方差分析在進行方差同質性檢驗時模型只能指定一個因素變量。在本研究中，多重比較的因素變量為載畜率，相應的區組變量成為重復變量。也就是說，當進行方差同質性檢驗時，涉及的待比較因素只有一個，那就是CHL，即載畜率變量。當方差同質性檢驗通過時(一般要求P>0.05)，說明不同載畜率下3個區組的觀測數據來自同一總體，即荒漠草原不同載畜率下短花針茅高度、密度來源于同一總體，其差異僅是由載畜率和區組差異引起。經檢驗發現，短花針茅高度F=0.80，P=0.5294；密度F=2.26，P=0.1587；P值均大于0.05，認為不同載畜率下的高度、密度指標沒有因載畜率不同而產生差異，也就是說不同載畜率下高度、密度數據具有方差同質性，來源于同一個總體。

2.4 線性可加性檢驗

獲得的樣本數據，正態性和方差同質性檢驗通過后還需要進行線性可加性檢驗[5]，即公式(1)的模型檢驗。在進行線性模型線性可加性檢驗時，研究者往往過于看重F值和Pr>F值。看重F值的原因是根據相對大小進行變量取舍，以便在多因素模型中進行模型優化；看重Pr>F值的原因是判斷是否繼續進行多重比較的標準。然而，這種做法是欠妥當的，因我們線性可加模型是基于試驗設計對觀測數據的數學表述，所以擬合率的大小也是影響線性可加模型是否成立的關鍵指標[6]。本研究案例線性可加模型檢驗結果顯示，高度F=2.36，P=0.1633，R2=0.6625；密度F=6.67，P=0.0194，R2=0.8475；所以高度方差分析檢驗沒有通過，擬合率也比較低；而密度方差分析檢驗通過(P<0.05)，擬合率高達84.75%。

2.5 區組效應算不算一個因素

區組效應是不是一個因子，不同研究者具有不同的理解。茆詩松等[4]在編著的《試驗設計》中指出，在進行線性可加模型檢驗時，觀察區組效應是否顯著大于誤差效應是進行判別的依據，如果區組效應顯著大于誤差效應(P<0.05)，就要考慮區組效應的價值，當區組效應與誤差效應無顯著差異，則可直接劃歸為誤差效應。然而，蓋鈞鎰[7]在主編的《試驗統計方法》中指出，區組效應可以看成另一個因素。本研究認為，區組試驗設計前提要求區組內不同試驗處理的基本條件盡可能一致，不同區組間的差異可以大一些，同時在野外或田間生態學實驗中經常涉及山坡大小、水文條件甚至植被狀況等自然條件限制，在安排試驗時就應該盡可能考慮區組間差異，可以采用區組試驗設計進行單向控制[7]。如果沒有考慮，也不能進行補救的情況下，區組效應屬于隨機效應，如果進行單向控制，區組效應屬于固定效應，這時無論是隨機效應還是固定效應，方差分析線性模型不會改變，均屬于雙因素方差分析模型，對于試驗處理的檢驗不再是簡單的取舍問題，而是固定模型、隨機模型和混合模型的問題[5]。這樣隨之而來會帶來另外的問題，單因素區組設計當考慮區組設計為因素時，不能考慮交互作用(沒有重復，缺少自由度)，所以也就不能判斷處理因素強弱；進而考慮區組因素為隨機因素時，不能對處理因素進行有效的檢驗(缺少自由度)。因此，這也成了單因素區組試驗設計的缺點。

3 方差分析結果的呈現

3.1 方差分析表呈現

在方差分析結果呈現時，研究者對方差分析結果進行了精簡(只有F值和Pr>F值)，我們只能看到因素的方差效應是否大于誤差效應，難以看到因素效應的方差貢獻，更看不到線性可加模型對原始數據的擬合效果，所以對于數據分析結果的科學性和可信性存在質疑。同時，對于存在隨機因素的多因素方差分析模型，我們也無法判斷采用的是固定模型、隨機模型或混合模型中的哪一類。因此，綜合來說方差分析結果應該采用表2的樣式。對于單因素隨機區組試驗設計，其方差分析模型應該是雙因素無交互作用方差分析模型(表2)。對于高度數據，其更符合單因素方差分析模型，此時區組效應屬于隨機效應，且對因素載畜率(CHL)具有干擾作用，因此采用單因素方差分析模型更為合適(此時區組效應成為隨機誤差效應)。盡管模型選擇是以損失擬合率為代價，但是擬合率下降幅度不大，且能夠表征載畜率因素對短花針茅高度的影響，所以結合多重比較結果(圖1)，單因素方差分析模型更為準確。對于密度指標，采用雙因素固定效應方差分析模型更為合理，此時具有較高的擬合率(R2=84.75%，即0.8475)，且載畜率對密度的影響也能夠得到真實體現。所以，單因素區組試驗設計的方差分析本質是雙因素方差分析模型，而且處理效應與區組效應劃歸為固定效應，模型為固定效應模型，即全稱應該為雙因素固定效應方差分析模型。然而，在分析數據時受區組效應的影響，究竟是采用單因素方差分析模型還是雙因素固定效應模型，需要通過檢驗結果進行判定。

3.2 多重比較結果呈現

在進行方差分析時，當方差分析檢驗結果顯著時(P<0.05)需要對樣本均值進行多重比較，且在概率水平下(一般P=0.0500或P=0.0100)進行差異顯著性標記[5]。從多重比較結果來看，高度指標在不同載畜率下存在顯著性差異(重牧的HG處理區短花針茅種群的高度顯著低于CK和LG，P<0.05)，且伴隨載畜率增大具有下降的變化趨勢，因此多重比較結果印證了單因素方差分析模型的合理性(表2)。從密度比較結果來看，CK和LG處理區短花針茅密度顯著低于MG和HG處理區(P<0.05)，結合擬合率，所以選用雙因素固定效應模型更適合。

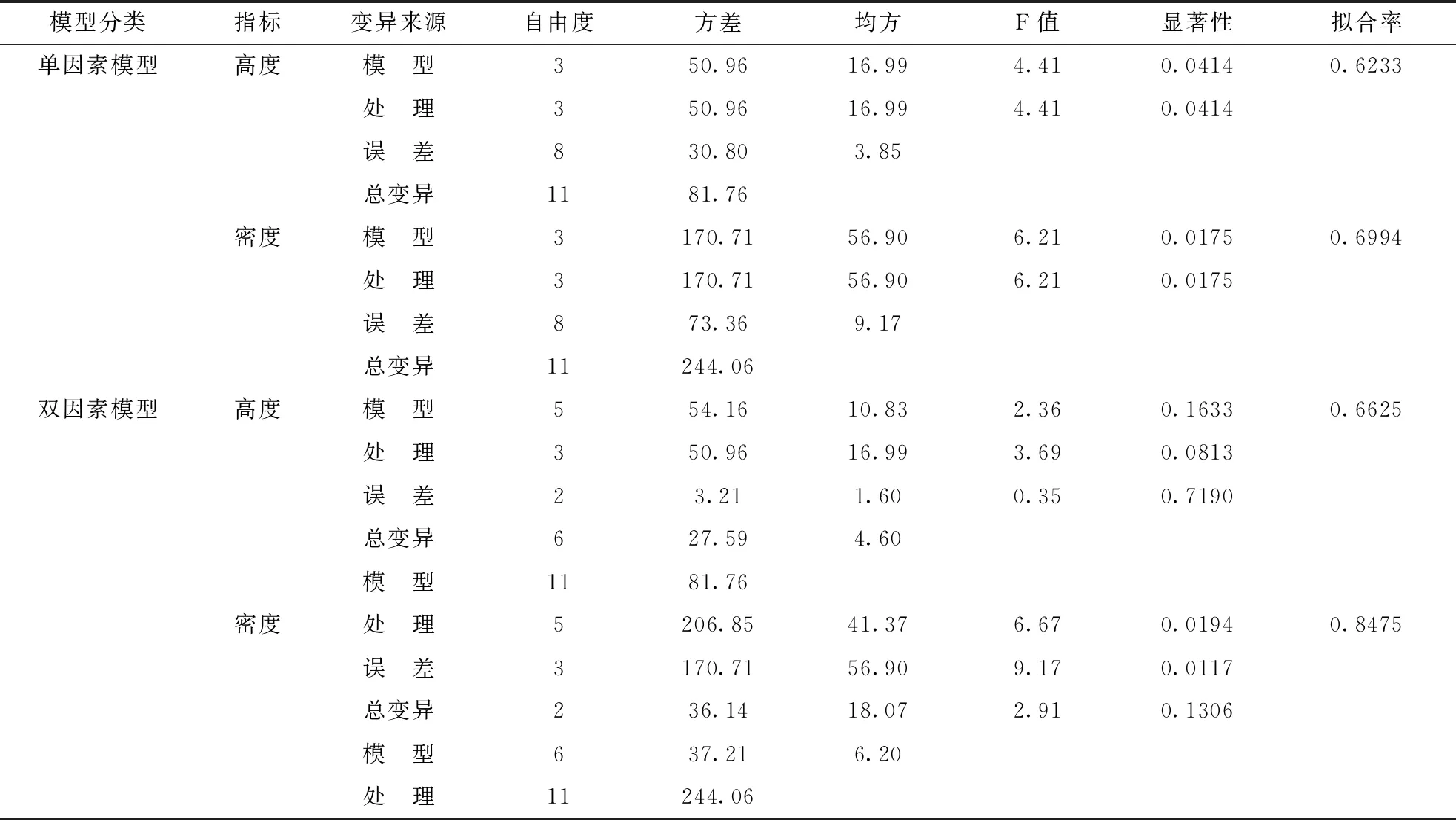
表2 荒漠草原短花針茅高度和密度方差分析表

4 討論

4.1 方差分析和多重比較的合理性選擇

多數情況下，研究者認為方差分析最簡單，其最善于利用方差分析解決問題。然而,事實上方差分析最不簡單，主要體現在以下幾個方面:首先，方差分析3個前提假設(正態性、同質性和線性可加性均)需要進行嚴格的檢驗[5]；其次，方差分析的線性可加模型依賴于試驗設計，有什么樣的試驗設計就會有什么樣的數據分析方法，主要針對的就是方差分析[4]；第三，方差分析模型[5]存在單因素模型、雙因素模型(又分有重復模型和無重復模型)和多因素模型(也分為有重復模型和無重復模型)；第四，按照因素是否為固定效應和隨機效應，方差分析模型又分為固定模型、隨機模型和混合模型[5]；第五，綜合前四項條件，選擇合理的方差分析模型并對數據進行科學分析是很困難的，甚至有時候方差分析這一方法不能應用。綜上所述，方差分析需要考察樣本容量對象、前提假設檢驗、試驗設計種類、試驗因素類別判定、線性可加模型及其擬合效果等諸多因素，期待在以后的研究中能夠看到基于多方面考量的方差分析運用過程，進而保證數據分析佐證科學問題的可靠性和科學性。

4.2 方差分析結果呈現的發展趨勢

方差分析結果更多的是以多重比較結果呈現[13～15]，但隨著數據可視化理念的提倡，表格呈現方式逐漸被圖形呈現方式替代。圖形呈現方式伴隨著計算機技術的提高，也存在發展趨勢，即柱形圖→柱形圖+誤差線→箱線圖。目前，柱形圖+誤差線表示方法最多，但是值得注意的是誤差線究竟是用標準偏差還是用標準誤差，不同的研究者具有不同標注方法[16]。在統計學中，如果誤差線采用的是標準偏差，表示獲得樣本數據為大樣本數據(樣本容量n≥30)，此時代表的統計學意義為樣本容量中有95%或99%的樣本觀測數據在此區間；如果誤差線采用的是標準誤差，此時代表的統計學意義為樣本均值有95%或99%的概率下在此區間內波動。由于是樣本均值的多重比較，且在野外或田間區組試驗設計中大樣本數據很難獲得，所以標注標準誤差更為合理[16]。除了多重比較結果，還有方差分析結果，這一結果最初研究者是采用全表放置[17～19]，但是隨著國際交流與合作的發展，簡表形式出現；原因是在生態學領域不是研究統計學結果，而是利用統計學表征生態學專業研究結果。這一想法或說法并沒有錯，但是讀者很難在多重比較結果和簡表中讀到數據擬合信息、模型選用信息，從而導致研究者在數據分析相互借鑒中產生偏差。因此，如果能交代清楚數據分析方法，建議盡可能交代清楚，比如單因素方差分析、簡單的雙因素方差分析；如果交代不清楚，建議將方差分析全表放上(如表2)，以便為讀者提供更為全面的數據分析信息，也方便研究者之間的相互借鑒。

4.3 關于P值的界定和使用

在進行方差分析和多重比較時，均涉及P值的界定，且近幾年關于P值的爭論比較激烈[8,20～23]；首先是P=0.0490和P=0.0500的問題，其次P值是否合理的問題，最終可以歸結為一個問題：P值究竟該怎么用，有沒有必要用。這一爭論最終以美國統計協會2019年給出的建議逐漸平息[9]：其認為在涉及概率統計的時候，標注P值的具體數值，不要過于強調是P=0.0500還是P=0.0100。本研究認為，P值是概率統計下的產物，是小樣本推測總體特征的保障，因此不能因P=0.0490和P=0.0500區別否定整個概率統計；其次，P值顯著臨界點的定義是根據小概率事件是否發生定義的[5]，所以P=0.0500和P=0.0100仍然可以沿用；第三，臨界點的定義從來都不是一成不變的，比如方差分析采用的臨界點是P=0.0500和P=0.0100，而回歸分析引入變量的臨界點一般是P=0.1500，所以臨界點的使用可以根據研究的專業內容進行合理的調整，比如張金屯[24]就有過相關的嘗試和實例。綜合來看，P值是進行概率檢驗的保障，不同的分析方法可以有不同的概率水平進行界定。比如方差分析，常用的臨界點P=0.0500和P=0.0100仍可沿用，視具體情況也可適當調整，比如P=0.1000；但也不可能無限制的增大臨界值，否則統計學的棄真和納偽錯誤發生概率就會發生變化，畢竟增大了概率臨界值也就增加了棄真錯誤的概率區間[5]。在SAS等統計軟件中，P值并不是固定的，數據分析者可以根據研究內容進行指定，也就是說統計軟件或統計學家也認為P值是可以調整的，從而適合不同研究專業和不同研究方向。結合美國統計學會針對P值的建議，方差分析還是要強調臨界值選用的具體數值(畢竟多重比較結果是在特定臨界值下計算的結果)，其他分析方法可以標注P值，然后根據自己的研究內容具體情況具體分析。此外，以后的數據分析，貝葉斯統計越來越受到統計學家的支持，生態學領域的數據分析也應該傾向于此。

5 結語

單因素區組試驗設計的方差分析模型應該是雙因素固定效應方差分析模型，且不能考慮試驗處理效應與區組效應的交互作用；在方差分析過程中，如果存在區組效應干擾時，可調整為單因素方差分析模型；這個過程均需要對指標數據進行正態性、方差同質性檢驗，結合樣本容量和線性擬合率綜合探討方差分析的可靠性和科學性。在進行多重比較時，需要給定具體的P值；對應的方差分析模型、處理效應檢驗可以根據研究情況，對P值可做出合理的調整；建議方差分析模型、處理效應檢驗和多重比較檢驗的P值最好一致。