基于改進理想點模型的巖體結構面分級方法

王述紅， 朱寶強， 張 澤

(東北大學 資源與土木工程學院， 遼寧 沈陽 110819)

巖體由各種各樣雜亂無章的結構面和塊體組成，結構面按成因可分為原生結構面、次生結構面和構造結構面.大量的工程實踐表明，巖體的破壞常常是沿著控穩結構面的破壞，在工程擾動情況下，結構面的力學效應及巖坡和隧道的穩定性主要取決于結構面規模和工程地質特性[1-2]，因此對結構面進行“分級”對于進一步深入研究結構面特性[3]及分析巖體穩定性有重要意義.

目前，對于巖體分級[4-6]和圍巖分級[7-9]的研究較多，而針對結構面的分級方法，主要為宏觀分析，如谷德振[10]在1979年依據結構面的規模將其分為5級，然而該分級體系的宏觀性導致了其更適合于大范圍的區域地質穩定性研究，不便于指導工程實踐.張倬元等[11]又根據結構面對巖體力學行為的影響程度，將其劃分為貫通性宏觀結構面、顯現結構面和隱微結構面，該分級同樣較為宏觀.后來，向波等[12]在總結了前人研究的基礎上，加入了部分定量指標，并結合相關國家標準將結構面分為更加細致的5種級別.Sun等[13]結合四川省峨眉山某水電站工程，將現場結構面細分為4組9個亞類，為類似地區結構面的分級提供了參考.

上述研究均不同程度地推進了結構面分級體系的發展，但研究多為宏觀上的定性判斷，不便于指導工程設計和施工.鑒于此，本文將多指標評價的理想點模型引入結構面分級中，通過對模型權重求解進行改進，提出了一種基于改進理想點模型的結構面定量分級方法，并將該方法應用于重慶市興隆隧道現場實測的典型結構面分級中，將分級結果與實際工程進行對比分析，驗證了所提方法的可靠性和實用性.

1 結構面分級的多指標評價體系

影響結構面分級的因素有許多，本文對結構面的定量分級主要是結合向波等[12]提出的定性及半定量分級體系(見表1)，該分級體系中結構面分級的主要影響因素有：①結構面兩側巖壁巖性、強度及風化程度；②結構面的粗糙度；③結構面充填物性質；④結構面富水程度.

表1 結構面分級體系

根據以上所述各影響因素，為便于計算，指標應選取定量或半定量指標，對于定性指標，則應進行定量化處理，類比“巖體分級”[4-6]及“圍巖分級”[7-9]中指標選取方法和指標獲取可行性，確定以下7個指標對結構面分級進行定量表征，主要包括：泉流量(X1)、巖石基本質量指標(X2)、單軸飽和抗壓強度(X3)、巖體完整性系數(X4)、風化系數(X5)、充填系數(X6)、粗糙系數(X7)，并以此為依據將結構面分為5級，多指標分級體系如圖1所示.

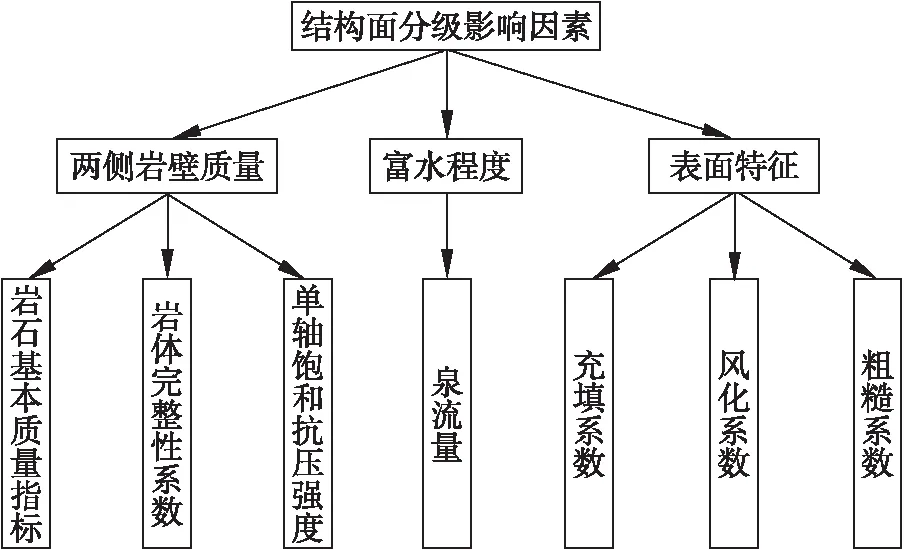
圖1 結構面多指標分級體系

2 結構面分級的改進理想點模型

理想點模型是由Hwang和Yoon[14]于1981年提出的基于多指標的多方案分析方法.該方法操作簡單，不需要復雜的計算過程，結果十分客觀[15].本文將其引入結構面的分級中，充分利用原始結構面數據信息，對結構面進行定量分級，并針對該方法權重確定較為主觀的缺點，提出了對該方法進行改進，利用層次分析法求得主觀權重；然后結合熵權法確定客觀權重，并利用最小熵原理優化主、客觀權重，由此確定分級指標的最優組合權重.建立結構面分級的改進理想點模型，從而對結構面進行合理分級，為后續抗剪強度確定及巖體穩定性分析奠定基礎.其主要流程如圖2所示，為便于工程應用，筆者基于Matlab平臺編制了該部分程序.

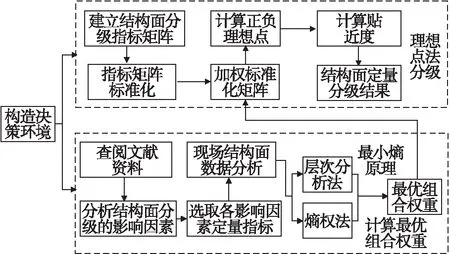
圖2 改進理想點模型分級流程

2.1 結構面分級指標量化

對于泉流量(X1)，結合實際工程確定其定量評價指標見表2.對于巖石基本質量指標(X2)、單軸飽和抗壓強度(X3)、巖體完整性系數(X4)，其指標量化采用國標分級標準，見表3.對于風化系數(X5)、充填系數(X6)、粗糙系數(X7)，結合GSI巖體質量分級法中的SCR部分確定其定量化評價指標，見表4.

綜上，可得到結構面分級各指標的定量化匯總結果，見表5.

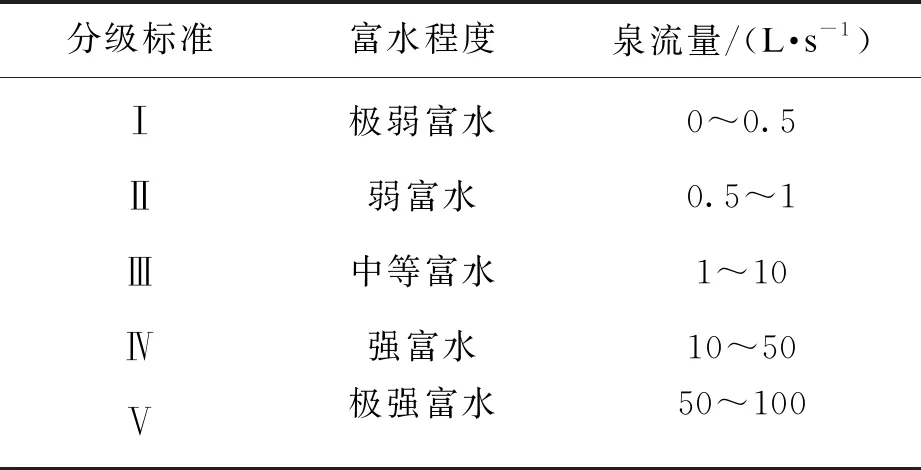
表2 結構面富水程度評價指標量化

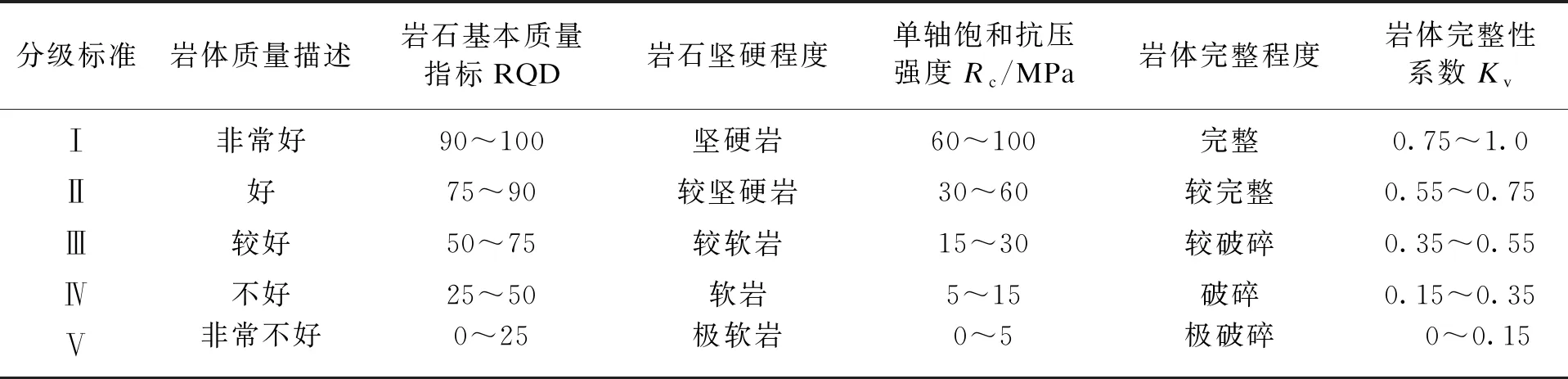
表3 結構面兩側巖壁質量評價指標量化

表4 結構面表面特征評價指標量化

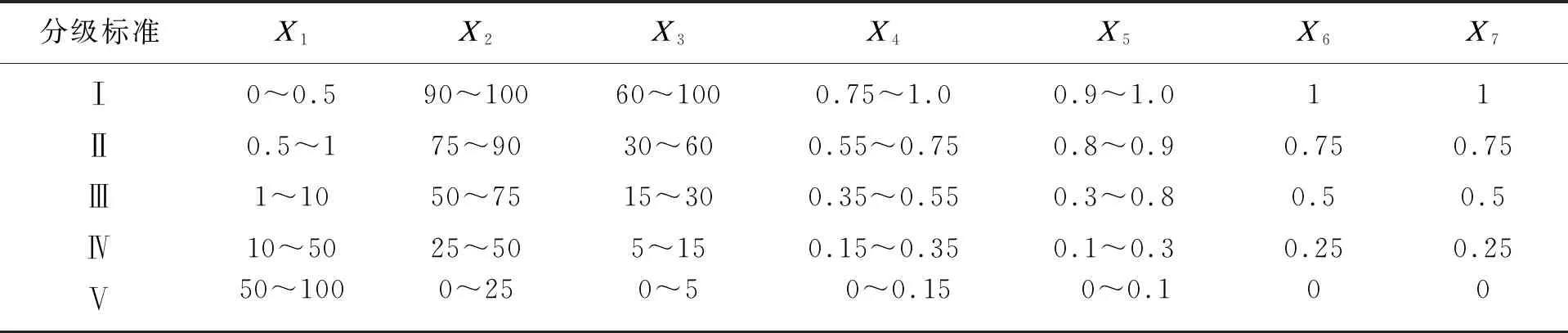
表5 結構面定量分級指標

2.2 建立分級指標矩陣

設有m個待分級結構面樣本，含有n個分級指標，對應的評估值xij(i=1,2,…,m;j=1,2,…,n)，則分級指標矩陣為

(1)

2.3 分級指標矩陣標準化

由于結構面各分級指標具有不同量綱及量綱單位，為了消除該影響，需要對指標進行無量綱化，經過標準化后的分級指標矩陣為

(2)

對于收益型指標：

對于消耗型指標：

2.4 加權標準化分級指標矩陣

2.4.1 層次分析法確定主觀權重

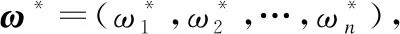
2.4.2 熵權法確定客觀權重

熵權法是一種客觀賦權法，它僅依賴于數據本身的離散性，目前已經廣泛應用于工程技術領域，采用該方法確定分級指標客觀權重的具體步驟如下：

1)建立原始結構面數據評價矩陣：

P=(pij)m×n.

(3)

式中，pij為指標初始評價值.

2)歸一化原始矩陣，得到標準矩陣：

P*=(pij*)m×n，

(4)

(5)

3)設ωj′為第j個評價指標的熵權，即所求客觀權重，則

(6)

2.4.3 確定最優組合權重

為彌補單一賦權帶來的缺陷，本文利用層次分析法求得各分級指標的主觀權重ω*，利用熵權法確定客觀權重ω′，ω′=(ω1′，ω2′，…，ωn′)，以此來修正主觀權重，最終得到最優組合權重ω，為使三者盡可能接近，依據最小熵原理對主、客觀權重進行組合，即

(7)

然后利用拉格朗日乘子法得到最優組合權重為

(8)

2.4.4 加權標準化分級指標矩陣

將最優組合權重與標準化分級指標矩陣相乘，得到加權標準化矩陣F=(fij)m×n=(ωjyij)m×n，即

(9)

2.5 構建評價指標體系

2.5.1 理想點和反理想點的確定

評價指標一般分為收益型和消耗型[17-18]，收益型指標越大越好，消耗型指標越小越好，此時結構面所屬等級也就越低.本文中泉流量屬于消耗型指標，其余指標均為收益型.若指標單調變化，則可定義如下理想點和反理想點.

當指標為收益型時，定義

(10)

當指標為消耗型時，定義

(11)

2.5.2 構建理想點評價函數

各分級方案與理想點的距離采用歐氏距離來度量，具體含義為距離理想點越近，反理想點越遠，分級結果就越好，具體公式為

(12)

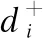
2.6 貼近度分析

對于一組結構面數據，當分級指標距理想點越近，距反理想點越遠時，表明該結構面等級越靠近理想點(即，等級越高)，該程度可以用貼近度β來表示，即

(13)

基于上述原理，可根據貼近度判斷各結構面所屬等級，判斷規則見表6.

3 工程實例

重慶市三環高速公路合川至長壽段興隆隧道位于重慶市渝北區木耳鎮良橋村，隧道在構造上位于重慶-沙坪向斜北西翼與龍王洞背斜之間，隧址區圍巖巖性主要為侏羅系上沙溪廟組中風化砂巖和泥巖，巖體結構呈大塊狀，富水程度較低.

本文以現場實測的15條具有代表性的結構面數據為例，進一步驗證改進理想點模型應用于結構面分級中的可靠性和實用性，結合現場各工點原位試驗結果，采用文獻[12]所述方法確定各結構面所屬等級.

3.1 確定無量綱化分級指標矩陣

對實測的15條結構面的各分級指標按式(2)進行無量綱化，得到無量綱化的分級指標見表7.

3.2 確定分級指標的組合權重

利用層次分析法，結合結構面特征參數及專家意見，確定各分級指標的主觀權重為

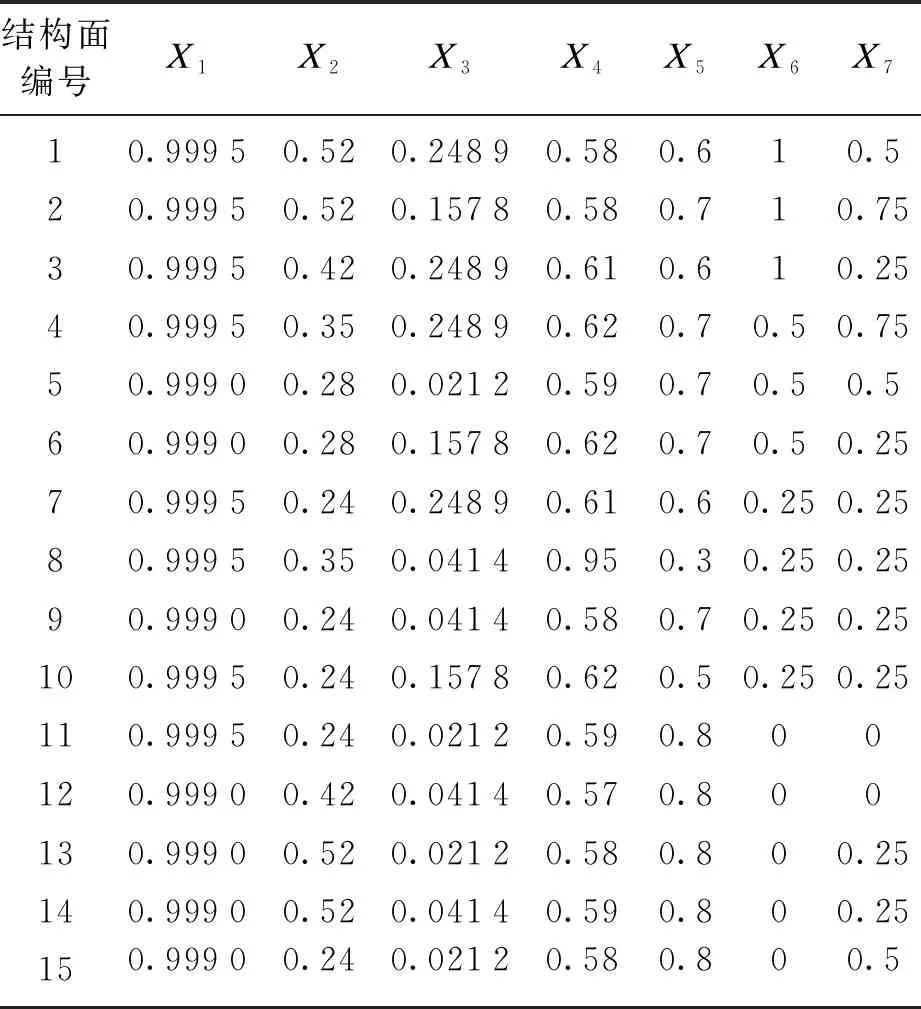
表7 實測結構面分級指標(無量綱化)

ω*=(0.108 7,0.110 7,0.142 5,
0.085 7,0.079 5,0.308 2,0.164 7).

然后利用式(3)～式(6)中熵權法計算得到各分級指標客觀權重為

ω′=(0.031 7,0.085 0,0.280 8,
0.053 4,0.069 3,0.302 1,0.177 7).

然后由式(7)，式(8)確定最優組合權重為

ω=(0.074 4,0.069 4,0.210 7,
0.026 5,0.049 5,0.389 6,0.189 9).

3.3 加權標準化分級指標矩陣

確定最優組合權重后，將表5中分級指標無量綱化，并結合表7中無量綱化后的15條實測結構面，代入式(9)可求得加權標準化分級指標矩陣為

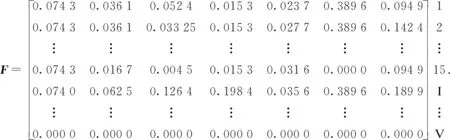
3.4 確定理想點和反理想點

將加權后的標準化矩陣代入式(10)，式(11),可求得理想點與反理想點為

3.5 確定貼近度

將3.3節及3.4節計算結果代入式(12)，式(13)，確定實測結構面及各等級結構面貼近度分別見表8和表9.

3.6 結果分析

結合表6中分級標準及表8和表9中貼近度計算結果，確定各條結構面所屬分級結果見表10，各方法與實際分級數量的誤差對比結果如圖3所示.

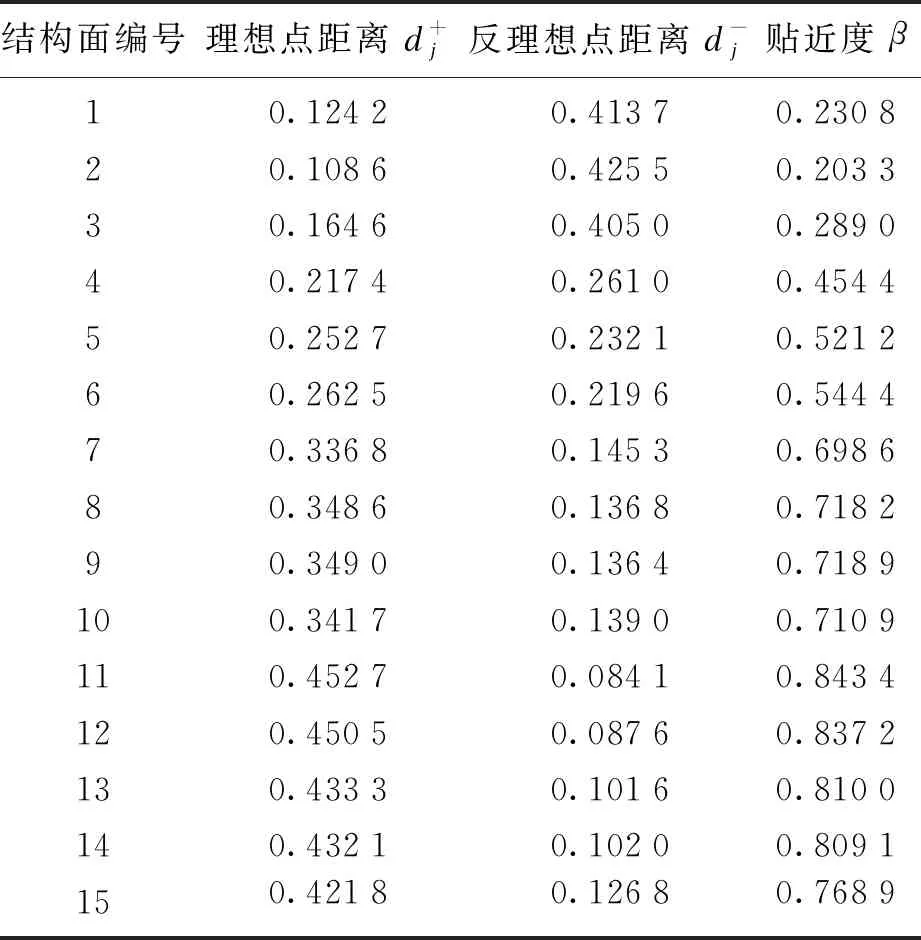
表8 實測結構面貼近度計算結果

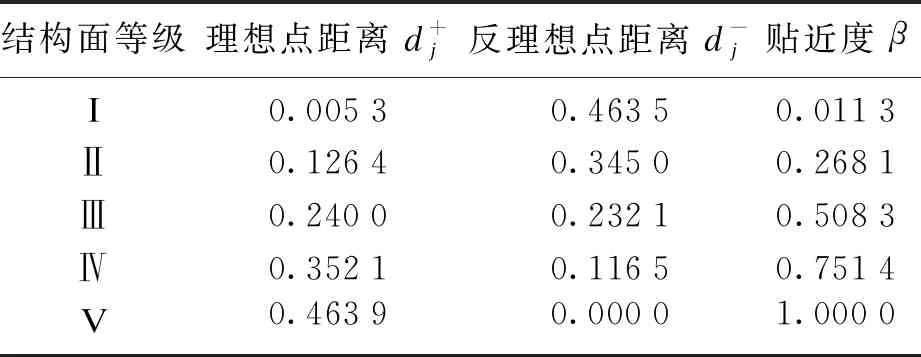
表9 各等級結構面貼近度計算結果

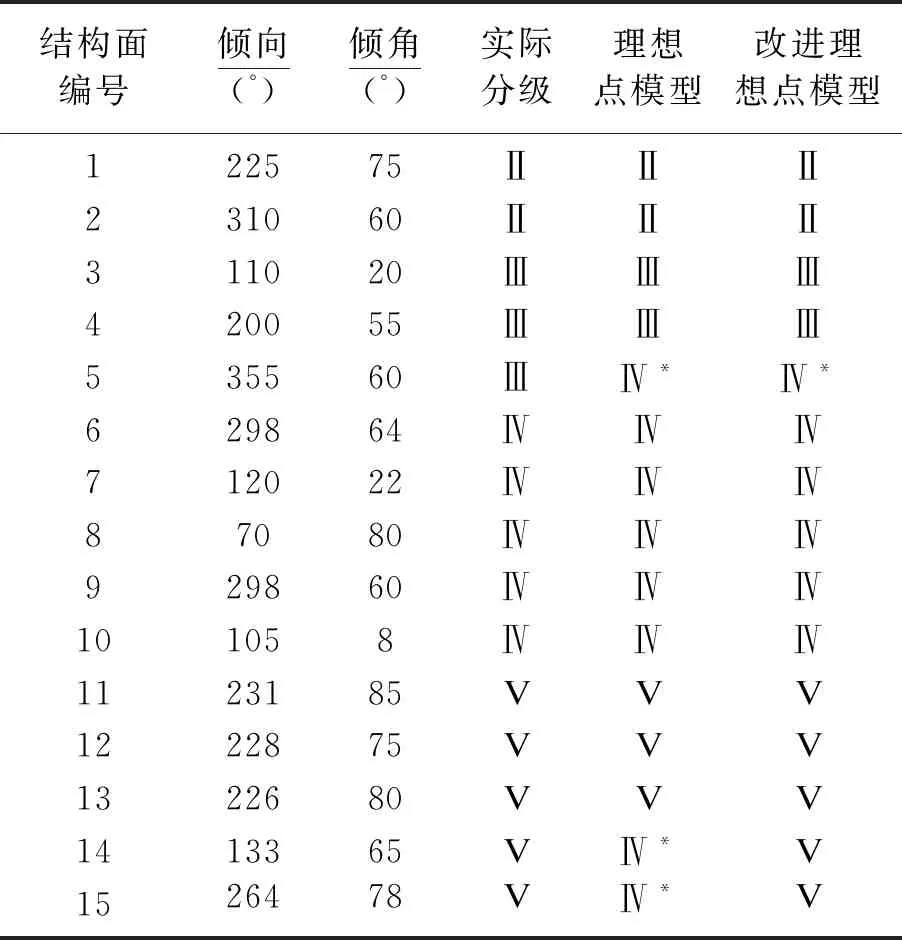
表10 結構面定量分級結果

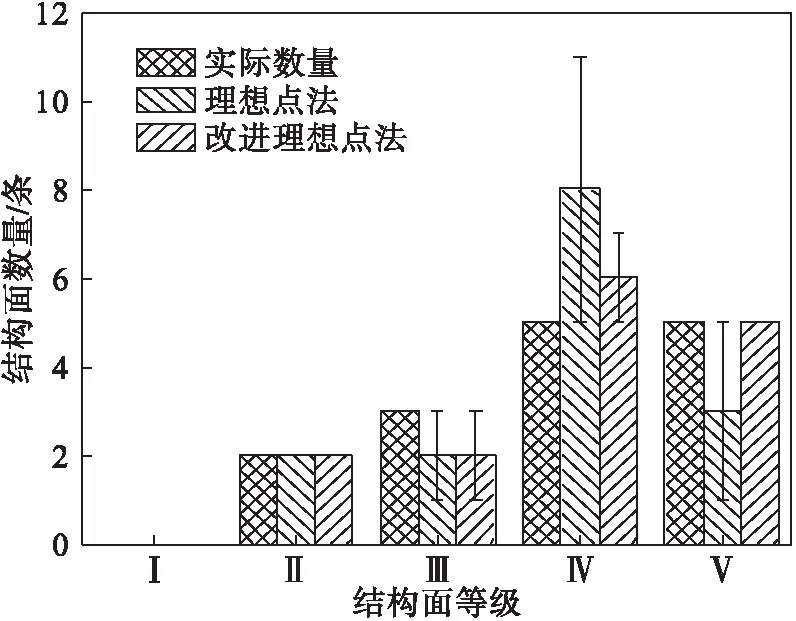
圖3 結構面分級結果誤差對比

由表10及圖3中的對比結果可知，本文所提改進理想點模型在應用于結構面分級時，僅第5條結構面等級劃分結果(Ⅳ級)略高于實際分級(Ⅲ級)，整體分級結果與實際較為接近.進一步分析出現分級偏差的結構面可知，該結構面貼近度計算結果為0.521 2，與分級標準中的0.508 3較為接近，分級時將介于兩級之間的結構面判別為其中一級，事實上，由于結構面等級越高，其性質也越差，因此按高等級結構面分析實際工程時更有利于保證施工安全，即判別結果偏于保守，也說明了本文方法具有一定的可行性.另外，改進理想點模型分級的準確率為93.3%(1條分級出現偏差，14條分級準確)，遠優于改進前理想點模型(準確率80%，3條分級出現偏差，12條分級準確)，表明了本文方法應用于結構面分級中具有較好的工程實用性.

4 結 論

1)本文考慮結構面分級的多種影響因素，利用7個常用指標進行定量化表征，建立了多指標的結構面定量分級體系，并依據最小熵原理對層次分析法及熵權法所求權重進行優化，避免了權重求解的主觀性，將所求最優組合權重引入到理想點模型中，構建了較為客觀的結構面定量分級模型.

2)將改進的理想點模型應用于重慶市興隆隧道現場實測的結構面分級中，其分級準確率達93.3%，分級結果與實際情況更為吻合，且遠優于改進前的準確率(80%)，說明所提方法實際可行，為巖體結構面定量分級提供了一種新的方法.

3)理想點模型作為一種多目標決策評價方法，在應用其進行結構面分級時，評價指標體系仍有待完善，嘗試用更科學的方法確定各指標的動態組合權重，將會使結構面分級結果更為準確且符合實際.