直葉片動態效應水動力特性實驗研究
王利東, 王 龍, 陳 兵, 永田修一, 村上天元
(1.大連理工大學 海洋科學與技術學院, 遼寧 盤錦 124221; 2.佐賀大學 海洋能研究所, 佐賀縣 佐賀市 8408502)
0 引言
翼型動態效應是一個非定常流動的分離現象[1],其會導致動態失速角明顯超過靜態失速角,并嚴重影響翼型的氣動力/水動力性能(如翼型的升力系數峰值增大、阻力系數驟然增大等)。 在工程問題中,翼型的動態效應是須要著重考慮的一個因素。 許多學者針對翼型的動態效應進行了大量研究[2]。 D E Shipley 的研究表明,須要考慮直升機飛行時的動態失速,否則會造成機翼俯仰力矩的增大以及氣動中心的失穩,嚴重影響直升機的安全飛行[3]。 祝健的研究表明,翼型動態效應會影響風力機葉片的穩定性,并縮短風力機葉片的使用壽命[4]。 因此,研究翼型的動態效應具有十分重要的意義。
目前,研究翼型動態效應的手段主要有3 種:數值模擬[5]、半經驗工程模型和實驗方法[6]。 針對二維翼型的動態效應,國內外學者做了大量數值模擬研究。 Kaufmann K[7]對俯仰翼型進行了動態失速實驗和數值模擬,研究結果表明,數值模擬中第一次出現失速的區域和實驗結果相一致,數值模擬在葉尖區域出現了更強的分離現象和更大的滯后效應。 Kim Y[8]用CFD 方法研究了自由流湍流對翼型動態效應的影響,分析了翼型上游的湍流以及湍流強度對翼型的影響。 Hand B[9]用數值模擬的方法研究了垂直軸風力機翼型在高雷諾數下的動態失速, 比較了U-RANS 和DES 方法對NACA0018 翼型的動態效應的影響, 發現增加雷諾數有利于提高機翼的氣動性能。 除了數值模擬研究外, 學者們對翼型的失速也進行了大量實驗研究。 劉清照[10]通過水槽實驗研究了NACA0018葉片在靜態下的水動力特性。 李國強[11]通過風洞實驗研究了風力機葉片的動態失速。
本文重點分析了直葉片在不同轉速下的水動力特性,以及在相同轉速不同來流速度下的升、阻力系數的變化趨勢, 從而為翼型的動態失速研究提供一定的參考。
1 實驗方法
1.1 模型參數
本實驗以NACA0018 翼型作為實驗模型,該翼型具有較好的水動力特性, 被廣泛應用于垂直軸潮流能水輪機上。 圖1 為NACA0018 翼型圖。
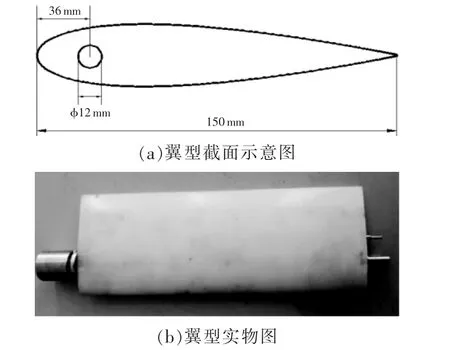
圖1 NACA0018 翼型圖Fig.1 NACA0018 airfoil blade
如圖1 所示,翼型的弦長為150 mm,葉片的旋轉中心距離葉片前緣36 mm, 葉片旋轉中心處旋轉軸的直徑為12 mm。
1.2 實驗設備
本實驗在日本佐賀大學伊萬里海洋能研究所進行。 實驗水槽高度為1 m,寬1 m,水深恒定為0.7 m,來流流速為0~1.5 m/s。圖2 為實驗裝置圖。實驗裝置包括三腳架、25 W 調速電機、轉動裝置、傳感器、聯軸器和葉片。三腳架的水平平面固定在水槽上方的桁架上,利用垂直平面固定調速電機;調速電機與轉動裝置上部相連接, 轉動裝置包括軸、軸承和凸輪結構等結構;轉動裝置下方連接美國ATI Mini45 六軸力/力矩傳感器, 該傳感器在x,y 方向上的量程為100 N,z 方向上的量程為700 N,且傳感器的精度為千分之一,能夠充分保證所測數據的準確性;傳感器下方連接葉片。實驗時,啟動調速電機,電機帶動傳動裝置使葉片以不同的擺動速度在0~30°內轉動。

圖2 實驗裝置Fig.2 The experimental device
1.3 實驗內容
實驗內容主要分為葉片靜態分析和動態效應分析。其中:靜態分析為測完一個來流迎角的水動力性能后,不斷地改變來流迎角,逐個求解,此時翼型處于靜止狀態;動態效應為在電機的帶動下,葉片不斷改變來流迎角,測得葉片的水動力性能。
1.3.1 靜態分析
初始來流速度為0.5 m/s,然后加速至0.8 m/s,測量該過程中葉片受力的變化; 來流速度從0.8 m/s 不斷減速至0.5 m/s, 測量該過程中葉片受力的變化。 在來流加、減速過程中,葉片受力的歷時曲線如圖3 所示。
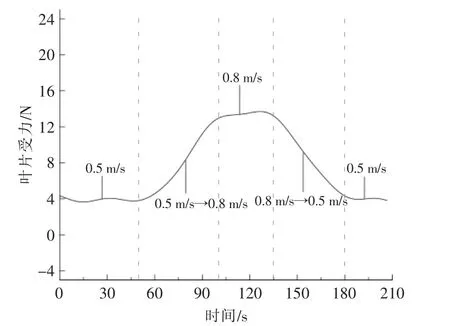
圖3 葉片受力的歷時曲線Fig.3 The history curves of the force acting on the airfoil blade
實驗時,來流速度可由傳感器測得,雷諾數的計算式為

式中:ρ 為水的密度,kg/m3;v 為來流速度,在來流加、 減速過程中v 取平均速度,m/s;c 為翼型的弦長,m;μ 為水的粘性系數,Pa·s。
由式(1)可知:當來流速度為0.5 m/s 時,對應的雷諾數為0.75×105; 當來流增大到0.8 m/s 時,雷諾數相應的增大到1.2×105, 即在本實驗中,雷諾數為0.75×105~1.2×105。翼型的水動力性能主要包括升力系數、阻力系數和升阻比等。 由六軸力/力矩傳感器測出葉片受到的升力FL和阻力FD,升力系數Cl和阻力系數Cd可分別由式 (2),(3)計算得到。
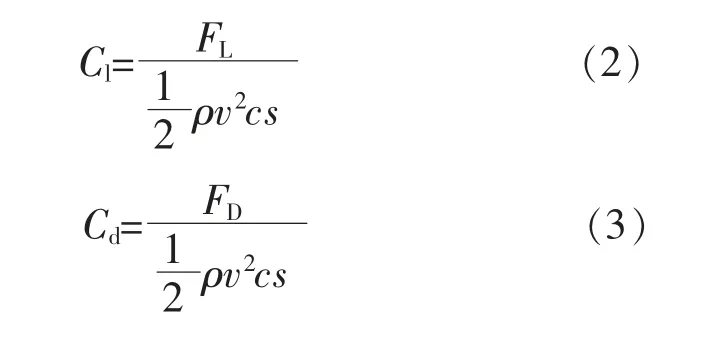
式中:s 為葉片的展長,m。
1.3.2 動態效應分析
在電機的帶動下,葉片以不同的擺動速度從0°開始轉動,轉到30°后,從30°再次回到0°,整個過程為一個周期。在本次實驗中,葉片采用3 種不同的擺動速度,即采用3 種不同的電機轉速,分 別 為ω1=0.115 rad/s,ω2=0.223 rad/s,ω3=0.345 rad/s。在葉片周期擺動的過程中,傳感器收集到多個周期下的葉片受力數據,根據式(2),(3)計算出一個周期下的升、阻力系數曲線。
2 結果與分析
2.1 加、減速過程中的葉片水動力特性
在來流加、減速過程中,葉片在不同來流迎角下的水動力系數變化曲線如圖4 所示。
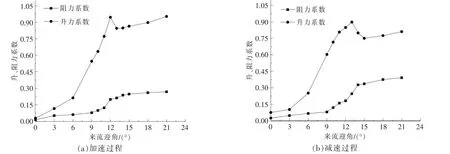
圖4 來流迎角對葉片水動力系數的影響Fig.4 The impact of the flow angles of attack on the hydrodynamic coefficients of the blade
從圖4(a)可以看出:隨著來流迎角的逐漸增大,葉片的升力系數也開始逐漸增大,當來流迎角增大到一定角度(葉片的失速角)后,葉片的升力系數突然減小,葉片的水動力性能急劇惡化,之后再逐漸增大來流迎角, 葉片的升力系數再次逐漸增大;隨著來流迎角從0°逐漸增大到21°,葉片的阻力系數一直處于增大狀態,而在失速角附近,阻力系數有一個突然增大的過程。 從圖4(b)可以看出,在來流減速過程中,葉片在不同來流迎角下的水動力系數的變化趨勢和來流加速過程中的基本相同,即在失速角附近,均出現了升力系數突然減小以及阻力系數突然增大的現象。
從圖4 中可以看出:在來流加速過程中,葉片的失速角為12°,此時的最大升力系數為0.92;在來流減速過程中,葉片的失速角為13°,此時的最大升力系數為0.90。 在來流加、減速過程中,葉片的失速角變化不明顯,即在葉片處于靜止狀態時,均勻增加來流的速度和均勻減小來流的速度,對葉片的影響基本相同。
2.2 同一來流速度不同轉速下的葉片水動力特性
保持來流速度不變, 啟動電機, 在電機帶動下,葉片以不同的擺動速度在0~30°內擺動。在本實驗中,葉片采用3 種不同的擺動速度,即采用3種不同的電機轉速來帶動葉片擺動。 當來流速度分別為0.5,0.6,0.8 m/s 時, 測得的葉片水動力系數曲線分別如圖5~7 所示。

圖5 來流速度為0.5 m/s 時的葉片水動力系數曲線Fig.5 The hydrodynamic coefficient curves of the airfoil blade when the inflow velocity is 0.5 m/s
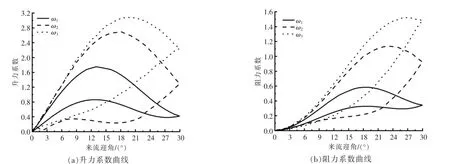
圖6 來流速度為0.6 m/s 時的葉片水動力系數曲線Fig.6 The hydrodynamic coefficient curves of the airfoil blade when the inflow velocity is 0.6 m/s
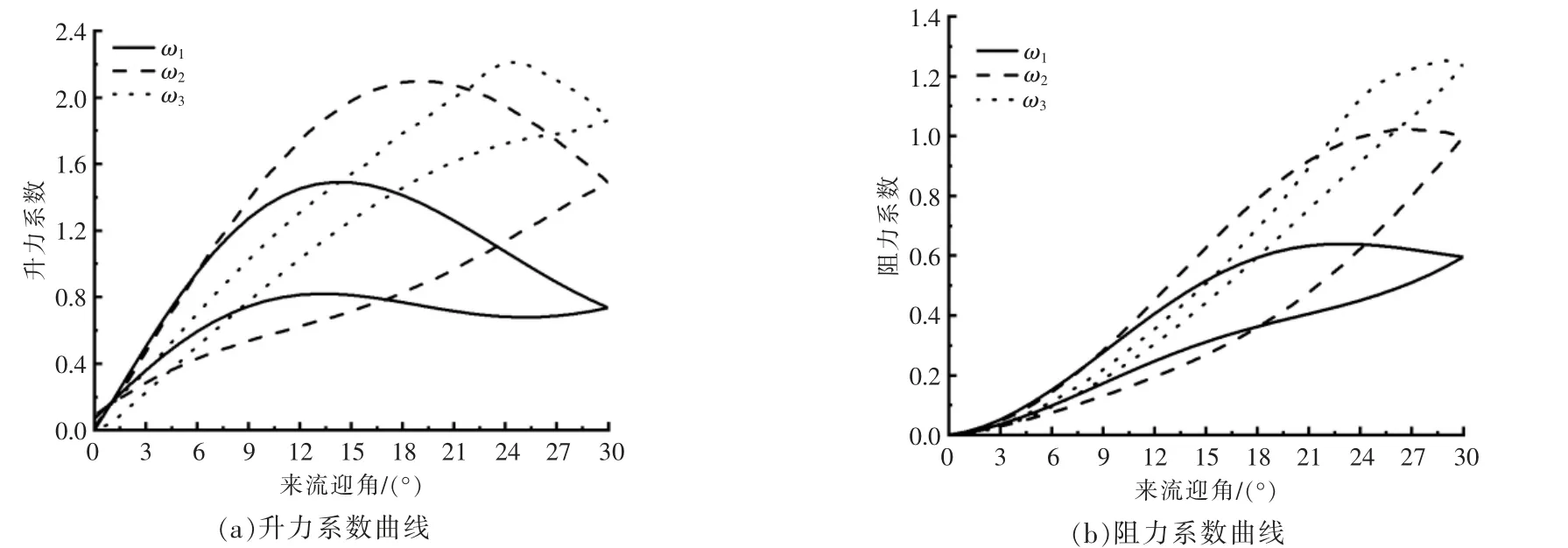
圖7 來流速度為0.8 m/s 時的葉片水動力系數曲線Fig.7 The hydrodynamic coefficient curves of the airfoil blade when the inflow velocity is 0.8 m/s
從圖5~7 中的升力系數曲線可以看出:當來流速度不同時,在整個周期運動的過程中,葉片的升力系數曲線均為閉合環形曲線: 在不同的轉速下,葉片的升力系數曲線有大致相同的變化趨勢;在0~30°這個階段, 葉片的升力系數隨著來流迎角的增加而逐漸增大,達到失速角后,葉片的升力系數開始逐漸下降;到達30°后,葉片開始往回運動,在30~0°這個階段,葉片的升力系數開始逐漸減小。 從圖5~7 中的阻力系數曲線可以看出,在0~30°這個階段,隨著來流迎角的增加,葉片的阻力系數逐漸增大, 并在失速角附近驟然增大;在30~0°這個階段,葉片的阻力系數逐漸降低到0。
在來流速度為0.8 m/s 的情況下,當電機轉速為ω1時,葉片的最大升力系數為1.49,失速角為14°;當電機轉速為ω2時,葉片的最大升力系數為2.0,失速角為19°;當電機轉速為ω3時,葉片的最大升力系數為2.2,失速角為25°。綜上可知,隨著電機轉速的不斷增大, 葉片的失速角不斷后移,且升力系數最大值不斷增大。這是因為轉速的增加導致葉片的局部雷諾數增加, 相應的失速角增大,而當轉速增大到一定程度后,葉片在0~30°內不會再發生動態失速的現象。 和靜態分析不同的是,在動態效應下,葉片升、阻力系數的最大值均大于靜態下的升、阻力系數最大值,且失速角和靜態下的也不同,失速延遲現象明顯。
2.3 同一轉速不同來流速度下的葉片水動力特性
電機轉速一定時, 不同來流速度對葉片升力系數的影響如圖8 所示。從圖8 可以看出,在固定電機轉速后, 來流速度對葉片水動力性能的影響具有一致性。以電機轉速為0.345 rad/s 為例,當來流速度為0.5 m/s 時,葉片失速角為18°;當來流速度為0.6 m/s 時,葉片失速角為19°;當來流速度為0.8 m/s 時,葉片失速角為24°。 綜上可知,當增大來流速度時,葉片的失速角不斷后移,這是因為來流速度的增大導致雷諾數增大, 而雷諾數的大小影響了升力系數曲線。 在圖8(a),(b)中,升力系數曲線有相同的變化趨勢, 即在來流速度增大的情況下,失速角不斷后移。
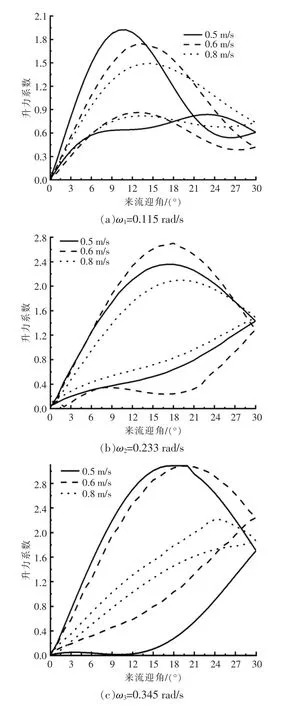
圖8 葉片在不同來流速度下的升力系數變化曲線Fig.8 The variation curve of lift coefficient of blade at different inlet velocity
3 結論
①在靜態分析情況下,來流在加、減速過程中對葉片的水動力特性影響基本相同, 均出現了在失速角附近升力系數驟然降低以及阻力系數驟然增大的現象。
②在動態分析情況下, 葉片的升力系數出現了“滯環”現象,NACA0018 翼型的失速角隨著電機轉速的增大而增大, 最大升力系數也隨之逐漸增大,電機轉速增大到一定程度后,可以降低動態失速的嚴重程度甚至避免其發生。
③與靜態分析相比, 翼型的動態失速角大于靜態失速角,失速延遲現象較為明顯。

