測試地面流程彎管沖蝕磨損的影響研究*

王健剛 孫巧雷 嚴淳鳀 馮 定 涂憶柳

(長江大學機械工程學院；湖北省油氣鉆完井工具工程技術研究中心)

0 引 言

隨著我國海洋油氣田開發技術日新月異的發展，海上油氣勘探開發任務不斷增多，油氣田測試作為開發過程中的重要環節，測試項目越來越多。在海上高產油氣田測試放噴過程中，普遍存在高產和高攜砂的特性[1-3]，地面流程在初次濾砂后，管道內仍有高速的水與砂礫，故管件受到一定程度的沖蝕磨損，嚴重時導致泄漏甚至發生重大事故。

針對管道的沖蝕問題，國內外部分學者展開了系統研究。李方淼等[4]探究了液固兩相流對活動彎頭的沖蝕規律，對活動彎頭的安裝角度和流速等因素進行了數值模擬。楊德成等[5]運用流體動力學計算軟件(CFD)對入口段長度及流體相關參數進行了分析。P.MAZDAK 等[6]對H-H管沖蝕機理進行了探索，發現嚴重侵蝕位置處于彎頭外壁頂部。黃勇等[7]研究了氣固兩相流對彎管結構的沖蝕影響。M.AMARA 等[8]通過使用CFD軟件對海水淡化設備彎管沖蝕預測進行了數值模擬，研究了流體及固體顆粒的影響。LIN N.等[9]在拉格朗日坐標系下研究了氣固兩相流對彎管沖蝕的影響規律。彭文山等[10]對彎管受含砂分散泡狀流體沖蝕機理進行了研究，通過試驗和數值模擬的方法分析了氣液分布和顆粒含量等因素對彎管沖蝕磨損的影響。王郭雨薇等[11]采用模擬試驗裝置對不同材料下沖蝕作用機理進行了研究。梁光川等[12]運用有限元軟件對管線內部流場進行了數值模擬。黎偉等[13]在拉格朗日坐標系下運用DPM模型研究了直徑60.3 mm彎管流速及顆粒對沖蝕率的影響。

上述研究大多基于單一因素對彎管沖蝕的影響，而對于海上地面流程的彎管多因素耦合分析鮮有理論研究。為此，本文基于海上某油氣田地面流程，針對地面流程中濾砂后的典型彎管結構，結合實際生產工況，對彎管不同流速、管徑比與顆粒含量進行數值計算與模擬分析，以期為管線設計與防護提供一定的參考。

1 計算模型

海底開采出的油氣經過地面流程中分離器后，將絕大部分水和砂礫等固體顆粒物分離出來[14-15]，管件內的液-固兩相流具有湍流特征。由于顆粒占比少，故可采用離散相模型進行計算。

1.1 控制方程

液相為連續不可壓縮的流動液體，采用Navier-Stokes方程求解，其方程為：

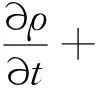
(1)

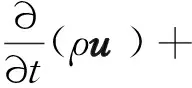
(2)

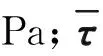
1.2 湍流模型

為保證模型滿足雷諾應力的需求同時又與真實值保持一致，得到更精準的平面、圓形擴散速度，選用k-ε模型，模型控制方程為：

(3)

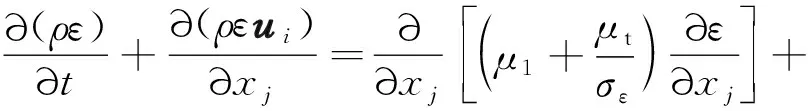
(4)

式中：k為湍流動能，J；ε為湍流動能耗散率，J/s；ui為平均速度，m/s；xj為空間坐標，mm；μ1為層間流動黏性系數；μt為湍流黏性系數；Gk為由速度產生的湍流動能；Gb為浮力所產生的湍流動能；Ym為可壓縮湍流動能產生的波動能；C1ε、C2ε、σk、σε為經驗常量；Sk、Sε為源項。

1.3 離散相控制模型

由于地面作業時地面流程入口短，一般會進行除砂處理，固體顆粒體積分數一般小于10%，可忽略粒子間的相互碰撞，同時液體為連續相，粒子為離散相。離散相固體顆粒受力控制方程為：

(5)

式中：u為連續相速度，m/s；up為離散相速度，m/s；ρp為離散相密度，kg/m3；ρ為連續相密度，kg/m3；FD為單位質量力，N；Fy為其他方向的作用力，N。

1.4 沖蝕磨損模型

根據Mixture-discrete phase model(DPM)分析法，考慮本研究影響沖蝕模型因素：管道形狀、連續相參數和顆粒參數，建立連續相與離散相相互耦合作用Erosion腐蝕模型。用于顆粒沖蝕率數值計算的模型為：

(6)

式中：Rerosion為彎管沖蝕率，kg/(m2·s)；C(dp)為離散相顆粒直徑函數；N為顆粒數目；mp為固體顆粒質量流量，kg/s；θ為固體顆粒與彎管壁面的碰撞角，(°)；f(θ)為侵入角函數；b(v)為滑移速度函數；Aface為彎管壁面計算單元面積，m2。

1.5 固體顆粒壁面碰撞模型

固體顆粒與彎管壁面碰撞后速度大小和方向都會發生變化。Grant模型通過壁面恢復系數來表示固體顆粒碰撞后方向與速度的變化，其中法向和切向的模型方程為：

εN=0.993-0.030 7θ+0.000 475θ2-
0.000 002 61θ3

(7)

εT=0.988-0.029θ+0.000 643θ2-
0.000 003 56θ3

(8)

式中：εN代表法向碰撞后恢復系數；εT代表切向碰撞后恢復系數。

2 地面流程彎管沖蝕數值模型

2.1 物理模型與網格劃分

選取地面流程中濾砂后的彎管幾何模型，如圖1所示，其管道分為入口段直管、彎曲段和出口段直管幾部分。采用掃掠的方式對地面流程彎管進行網格劃分。對彎曲段進行局部加密，入口段長度L1=300 mm，出口段長度L2=300 mm，管道內徑D=63.5 mm，彎管半徑R=200.0 mm。

圖1 幾何模型與網格劃分Fig.1 Geometric model and grid division

2.2 網格無關性分析

網格的質量及數量會對沖蝕磨損產生影響，因此有必要進行網格無關性檢驗[16]。將彎管模型劃分成472 656、641 646、1 085 175和1 954 554的網格數量，計算出不同網格數量下彎管沖蝕率，如表1所示。由表1可知：當網格數量從1 085 175增加到1 954 554時，網格數量增加80.12%，沖蝕率變化率為1.59%。為保證計算精度與速度，選用網格數量1 085 175進行分析計算。

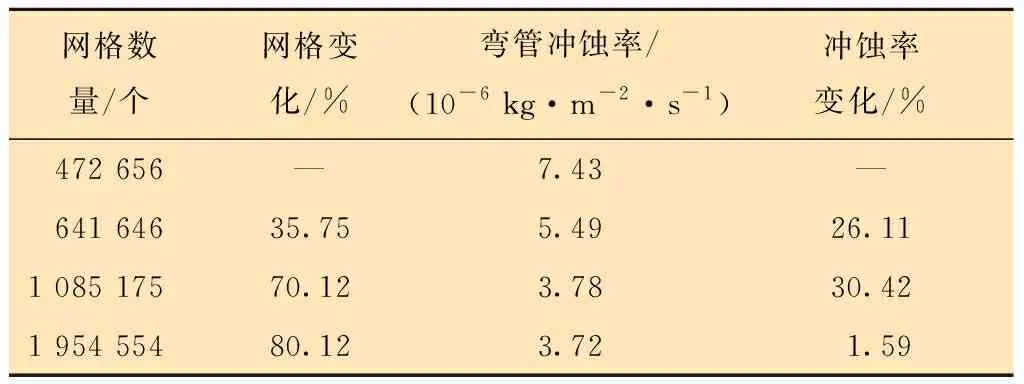
表1 不同網格數量下數值模擬結果Table 1 Numerical simulation results for different grid numbers

2.3 邊界條件

本文設置入口為速度入口，出口采用自由流出邊界，液相為連續相，固相顆粒為離散相。離散相通過注射的方式進入，其速度與流體速度相同。粒子類型設置為砂石，具體參數如表2所示。

表2 參數設置Table 2 Parameter setup

3 計算結果與分析

3.1 流場分析

由于地面流程井口流速在產量測試及開關井過程中變化較大，為分析地面流程測試作業過程中流體攜砂在彎管內部的流場變化情況，依據地面流程現場測試作業的相關數據進行數值模擬，選取入口速度為14～23 m/s，固體顆粒體積分數為0.05%，彎曲角度為90°進行分析。圖2為彎管壓力云圖。從圖2可以看出，在彎管幾何模型一定時，不同流速下彎管內部的壓力變化趨勢相同，具體分布為：從彎管入口段區域至彎管段，彎管內部壓力逐漸減小，當流體從直管入口段流經彎管段最后從直管出口流出，彎管段外側壓力變化趨勢為先增大后減小，彎管段內側與外側趨勢恰恰相反。這種現象是由于流體在流經彎管段時存在沿彎曲方向的離心力，使得流體由彎管內側向外側運動，導致彎管外側壓力大而內側壓力小。流體從彎管段流至直管出口段時，由于彎管處存在渦流，導致外側壓力逐漸減小、內側壓力逐漸增大。

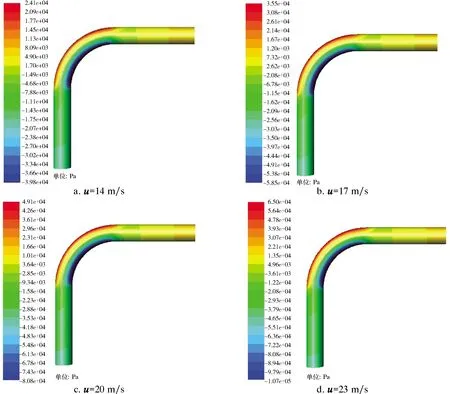
圖2 彎管壓力云圖Fig.2 Pressure cloud of bend pipe

3.2 顆粒運動軌跡及沖蝕磨損

選取固相顆粒體積分數0.05%，彎曲角度90°彎管作為計算模型，數值計算結果如圖3所示。

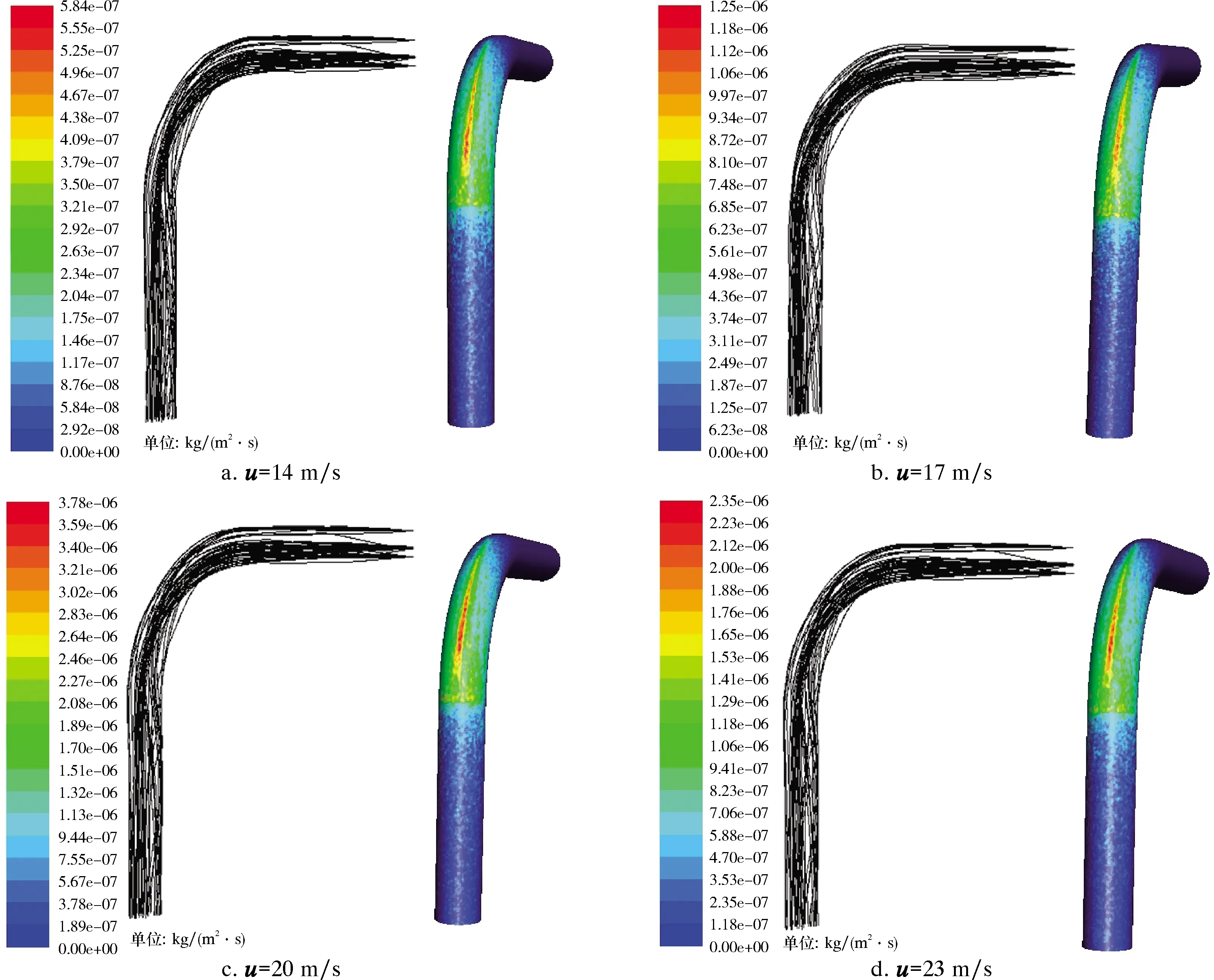
圖3 彎管顆粒運動軌跡及沖蝕磨損云圖Fig.3 Particle moving trajectory and erosion wear cloud of bend pipe

彎管沖蝕磨損最大位置在彎管段，在彎管直管入口段、出口段僅有著零星狀的沖蝕磨損，彎曲段處沖蝕磨損遠遠大于直管處。隨著入口速度增大，固體顆粒與壁面碰撞時的動能相應增大，同時單位時間內碰撞的顆粒個數增多，使得彎管外側沖蝕磨損增大較為明顯。流速與沖蝕率的關系曲線如圖4所示。而此時彎管段內側沖蝕磨損增大并不如外側明顯，主要原因在于，流速的增大導致彎管段壓力梯度以及離心力隨之增大，使得更多的固體顆粒向彎管段外側碰撞，固體顆粒碰撞后，隨流體繼續運動，在彎管段與直管出口段由于壓力改變產生的渦流導致固體顆粒的軌跡相較于直管入口段顆粒更加分散，直觀地反映在圖中，直管出口段的沖蝕效果更為明顯。

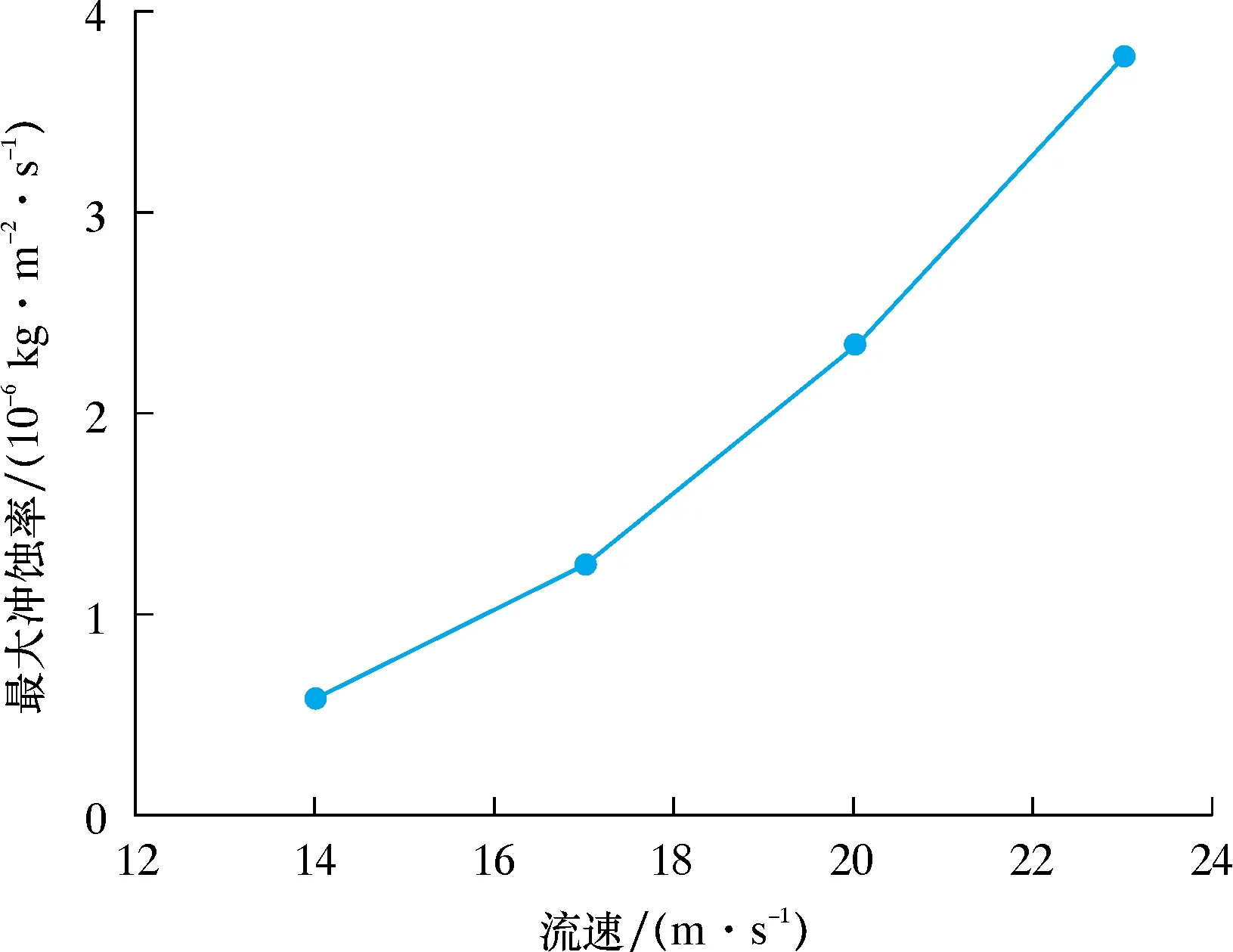
圖4 流速與沖蝕率的關系曲線Fig.4 Relationship between flow velocity and erosion

3.3 固相顆粒體積分數對彎管沖蝕的影響

選取流速23 m/s，彎曲角度90°彎管作為計算模型，固相顆粒體積分數與沖蝕率的關系曲線如圖5所示。地面流程彎管最大沖蝕率隨著顆粒體積分數的增加而近似呈線性增大，當顆粒體積分數增加時，同一時間內流體可攜砂數量上升，導致更嚴重的沖蝕。

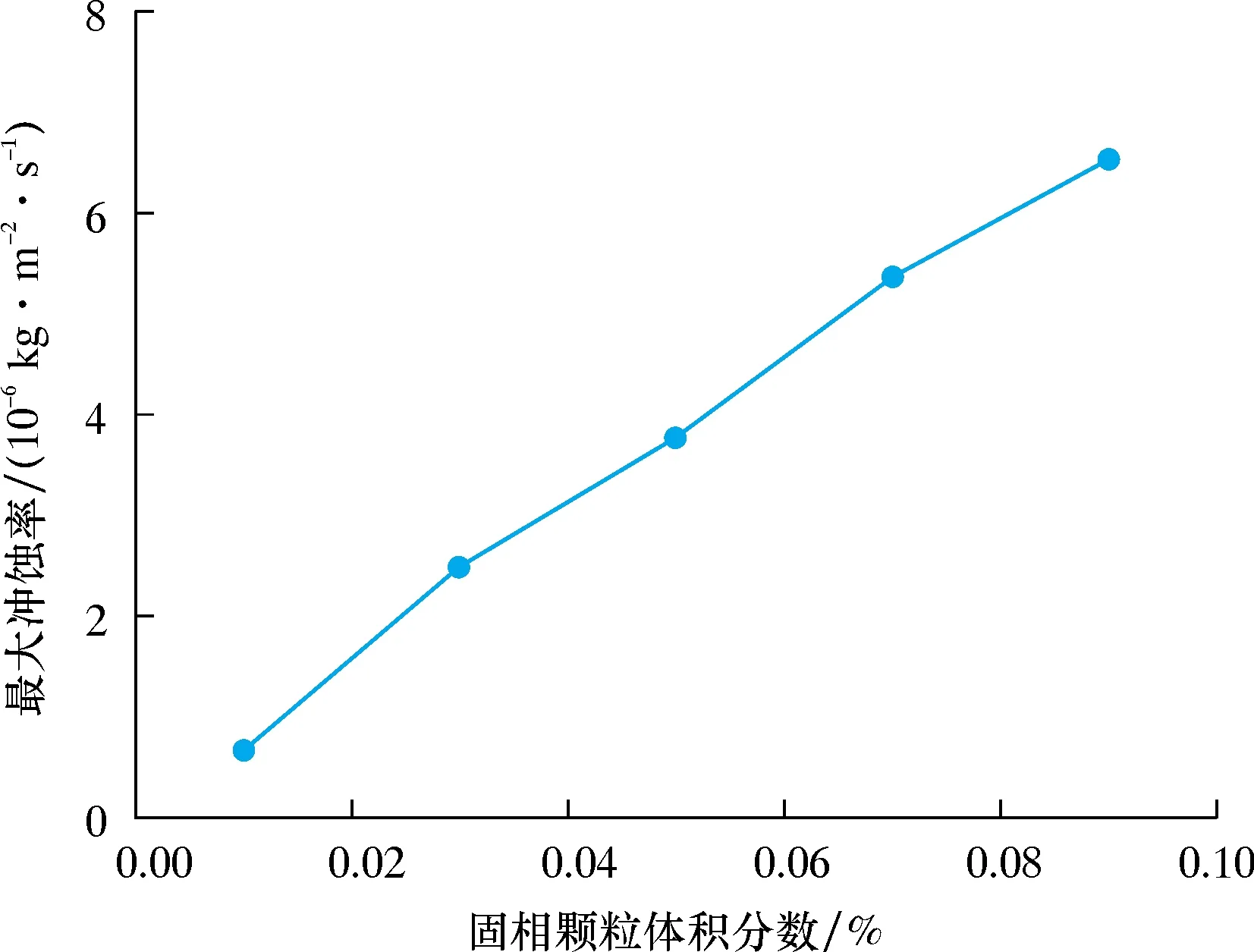
圖5 固相顆粒體積分數與沖蝕率的關系曲線Fig.5 Relationship between solid particle volume fraction and erosion

3.4 彎曲角度對彎管沖蝕的影響

選取流速23 m/s，固相顆粒體積分數0.05%彎管作為計算模型，彎曲角度與沖蝕率的關系曲線如圖6所示。

由圖6可以看出，地面流程彎管的最大沖蝕率隨著彎管彎曲角度的增加而增大，彎曲角度為45°時沖蝕率最小。主要是受其幾何模型影響，顆粒在彎管45°的彎曲角度時，固相顆粒碰撞角為小于90°的低攻角，使得彎管管壁法向速度分量較小；另一方面，隨著彎曲角度的增大，彎曲長度增加，可碰撞面長度增大，顆粒在流經該區域時彎曲段內壁受到顆粒多次碰撞。

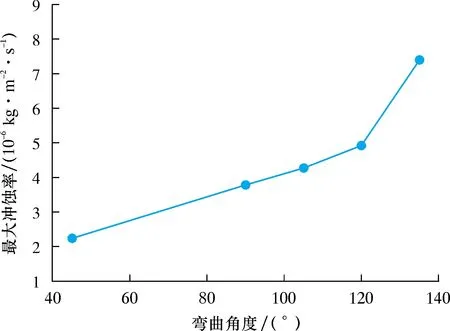
圖6 彎曲角度與沖蝕率的關系曲線Fig.6 Relationship between bending angle and erosion

3.5 流速與顆粒耦合沖蝕分析

考慮不同流速與不同顆粒體積分數的特征參數變化，綜合分析流速與顆粒體積分數耦合對地面流程彎管最大沖蝕率的影響，開展了流速為14～23 m/s，顆粒體積分數為0.01%～0.09%時地面流程彎管沖蝕磨損分析。不同固相顆粒體積分數與不同流速下彎管的最大沖蝕率曲面圖如圖7所示。

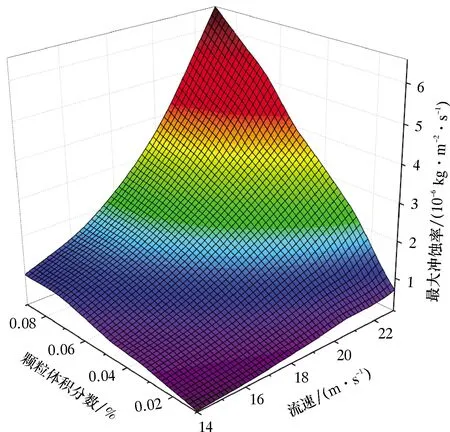
圖7 不同固相顆粒體積分數與不同流速下彎管的最大沖蝕速率曲面圖Fig.7 Surface diagram of the maximum erosion velocity of bend pipe under different solid particle volume fractions and different flow velocities

由圖7可以看出：當固相顆粒體積分數為0.01%、流速為14 m/s時，地面流程彎管最大沖蝕速率為1.29×10-7kg/(m2·s)，此時的沖蝕率為最小值；當固相顆粒體積分數為0.09%，流速為23 m/s時，地面流程彎管最大沖蝕速率為6.54×10-6kg/(m2·s)，此時的沖蝕率為最大值。隨著流速的增加可攜帶的固相顆粒能力隨之增大，流速與固相顆粒的耦合影響最高可達到50.7倍。當固相顆粒體積分數為0.07%～0.09%時，流體流速對沖蝕率的斜率小于固相顆粒體積分數改變對該斜率帶來的影響，即此時減小固相顆粒體積分數對減小沖蝕率更明顯。

3.6 流速與彎曲角度耦合沖蝕分析

考慮不同流速與不同幾何模型的特征參數變化，綜合分析流速與彎曲角度耦合對地面流程彎管最大沖蝕率的影響，開展了流速為14～23 m/s，彎曲角度為45°、90°、105°、120°及135°時地面流程彎管沖蝕磨損分析。不同彎曲角度與不同流速下彎管的最大沖蝕率曲面圖如圖8所示。

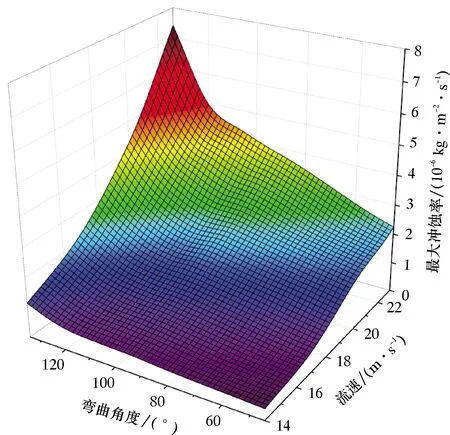
圖8 不同彎曲角度與不同流速下彎管的最大沖蝕率曲面圖Fig.8 Surface diagram of the maximum erosion rate of bend pipe under different solid particle volume fractions and different flow velocities

由圖8可以看出：在彎曲角度為135°，流速為23 m/s時，地面流程彎管最大沖蝕率為7.41×10-6kg/(m2·s)，此時沖蝕率為最大值；彎曲角度為45°，流速為14m/s時，地面流程彎管最大沖蝕速率為3.75×10-7kg/(m2·s)，此時沖蝕率為最小值，流速與彎曲角度的耦合影響最高可達到19.8倍，隨著流速的增大，彎管彎曲角度對沖蝕的影響增大。隨著彎管彎曲角度增大，最大沖蝕率增大，該趨勢伴隨流速增大漲幅趨勢更加明顯，設計時應優先考慮彎曲角度較小的彎管，若不可避免選取其他彎曲角度彎管時，建議調整該段流速以減小沖蝕率。

4 結 論

(1)地面流程彎管沖蝕磨損主要區域為彎曲段外側內壁，由于流體在流經彎管段時存在沿彎曲方向的離心力，使得流體由彎管內側向外側運動，彎管外側壓力大、內側壓力小，流體攜帶砂礫顆粒向彎管內壁外側碰撞，故應在主要沖蝕磨損區域進行重點監測。

(2)流速和固相顆粒體積分數對彎管的沖蝕規律相似，隨著流速和固相顆粒體積分數的增大，地面流程彎管的最大沖蝕速率增大，流速與固相顆粒的耦合影響最高可達到50.7倍；當固相顆粒體積分數處于0.07%～0.09%時，流速對沖蝕的影響小于固相顆粒體積分數改變帶來的影響；隨著彎管彎曲角度增大，最大沖蝕率呈現出增大趨勢，該趨勢伴隨流速增大漲幅趨勢更加明顯，流速與固相顆粒體積分數的耦合影響最高可達到19.8倍，地面流程彎管在彎曲角度為45°時沖蝕率最小。

(3)在實際地面流程布線和作業過程中，可以根據實際工況需求，綜合考慮不同彎曲角度帶來的影響，合理調整管道入口流體參數，這對于減小管道沖蝕磨損有著重要意義。