帶擾動的局部超二次Hamilton系統周期解的存在性

鄭玲玲，郭 飛

(天津大學數學學院，天津 300354)

1 主要結論

本文研究如下二階Hamilton系統：

(1)

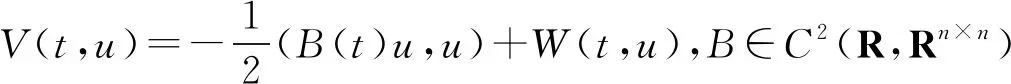
(A) 對任意x∈Rn，W(t，x)關于變量t是可測的；對a.e.t∈[0，T]，W(t，x)關于x是連續可微的；存在函數a1∈C([0，+∞)，[0，+∞))和a2∈L1([0，T]；[0，+∞))，使得

超二次條件在Hamilton系統研究中的使用可以追溯到20世紀.早在1978年，Rabinowitz[1]便提出了眾所周知的經典超二次條件(下稱(A-R)條件)，并得到了周期解的存在性.之后該條件在研究Hamilton系統周期解和同宿解等問題中被廣泛使用，如文獻[2].近年來，有許多學者使用了更弱的條件代替(A-R)條件.文獻[3]引進了比(A-R)條件更弱的超二次條件，即

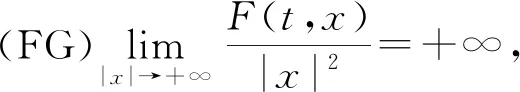
當f(t)≡0時，文獻[3]在條件(FG)下使用環繞定理得到Hamilton系統周期解的存在性.隨后，很多文獻都在(FG)條件下研究了系統(1)的周期解問題.[4-7]2018年，文獻[8]在研究非擾動系統同宿解的存在性時使用了比(FG)更弱的局部超二次條件.

當f(t)≡0時，研究擾動系統周期解問題的文獻極少.文獻[9]研究了一類帶擾動的一階Hamilton系統周期解的存在性和多重性，尚未發現對擾動系統(1)周期解問題的研究.關于擾動系統(1)同宿解存在性和多重性的研究的文獻也很少.文獻[10]在非線性項W滿足(A-R)條件下，得到了系統(1)同宿解的多重性.文獻[11]在非線性項W滿足(FG)條件下，得到了系統(1)同宿解的多重性.

受此啟發，本文對擾動系統(1)使用山路引理，考慮在非線性項W(t，x)滿足局部超二次條件(即下述條件(W3))時，系統(1)的周期解的存在性.本文結論如下：

定理1.1假設函數B(t)，W(t，x)，f(t)滿足條件(A)和下列條件：

(B)B∈C2(R，Rn×n)為對稱正定矩陣函數，且是T周期的.

(W1)W∈C2(R×Rn，R)，關于變量t是T周期的，W(t，0)≡0，W(t，x)≥0，對?(t，x)∈[0，T]×Rn成立.

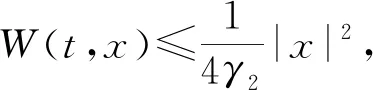
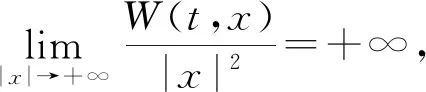
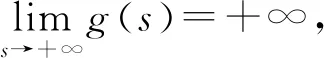
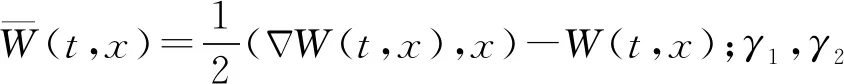
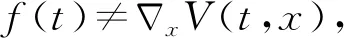
則系統(1)存在一個非平凡的周期解.

定理1.1在比(FG)條件更弱的局部超二次條件(W3)下，得到了擾動系統(1)周期解的存在性.本文擾動項f(t)為“真正的擾動”，即擾動勢能(f(t)，u(t))因為不滿足條件(W1)，所以不能被W(t，x)包含.有實例表明的確存在滿足本文定理1.1的函數，參見例4.1.

2 預備知識

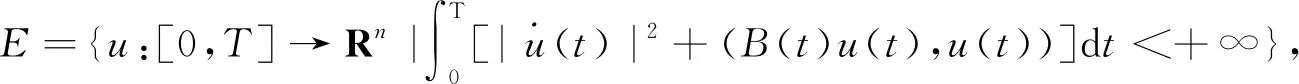
其上范數為

定義E上的泛函φ，

(2)

則有

(3)

由參考文獻[5]可知，在條件(A)下，φ∈C1(E，R)，且

(4)

引理2.1[12](嵌入定理)E緊嵌入Lp(ST，Rn)，p∈[1，+∞)，所以存在嵌入常數γp>0，使得

(5)

引理2.2[13](山路引理) 若X是一個Banach空間，I∈C1(X，Rn)，存在e∈X和常數ρ，α>0，使得

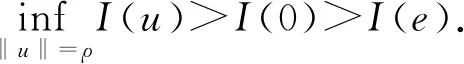
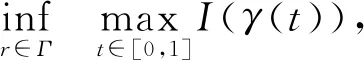
Γ∶={γ∈C([0，1]，X)|γ(0)=0，γ(1)=e}，

則c≥b是泛函I的一個臨界值.

注釋由文獻[14]可知，用(C)條件代替(PS)c條件，引理2.2依然成立，因此本文使用(C)條件.

3 定理1.1的證明

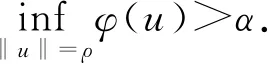
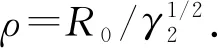
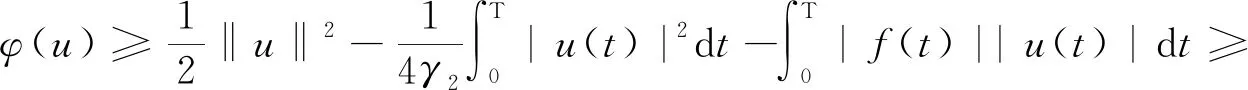
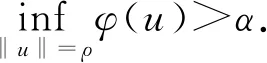
命題3.2假設(W1)，(W3)和(F)成立，則存在e∈EBρ，使得φ(e)<0.

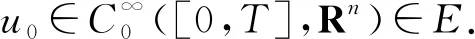
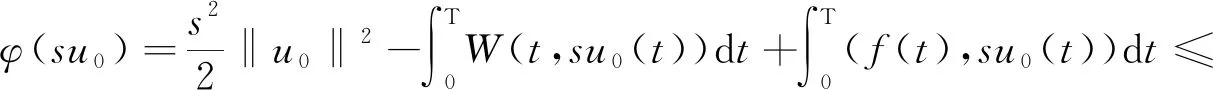
取s0>0，使得s0‖u0‖>ρ，則有φ(s0u0)<0=φ(0)，從而e∶=s0u0∈EBρ滿足要求.

命題3.3假設條件(W2)，(W4)和(F)成立.若存在{un}?E，滿足

φ(un)→c>0，〈φ′(un)，un〉→0，

(6)

則{un}在E上有界.

證明用反證法，不妨設‖un‖→+∞.令vn(t)=un(t)/‖un‖，則‖vn‖=1.由(3)，(5)，(6)式及假設(F)可得

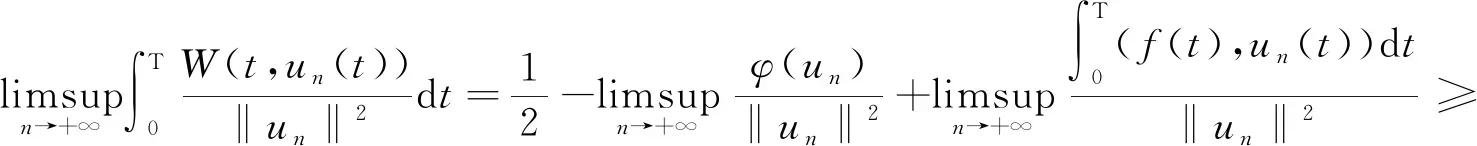
(7)

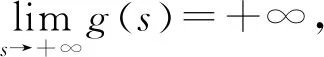
g(s)≥8(c+1)γ∞.

(8)

令

Θn={t∈[0，T]||un(t)|≥M}，

則由假設(W2)可得

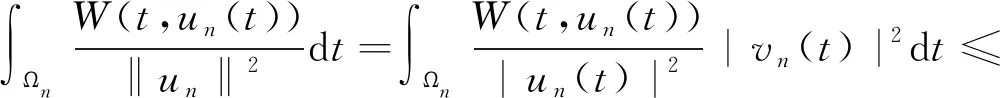
(9)

由(3)，(4)，(6)式及假設(F)，對?ε∈(0，1)可得

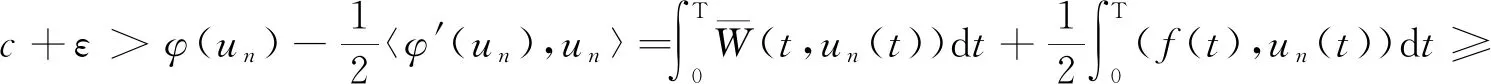
(10)

當n充分大時，由假設(W4)可得

(11)

因此，由假設(W4)，(8)，(10)和(11)式可得

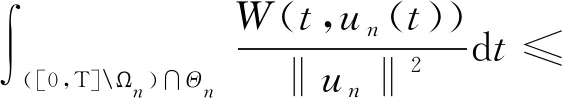
(12)

當n充分大時成立.同時有

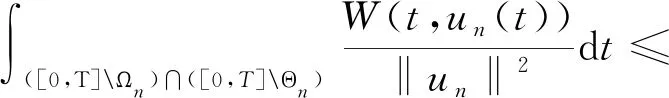
(13)

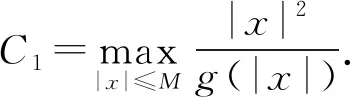
由(9)，(12)和(13)式可得

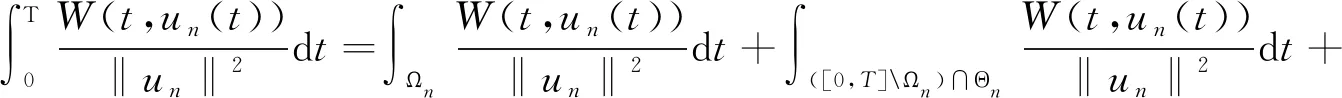
(14)

當n充分大時成立.(14)式兩邊同取上極限，由(7)式可得

顯然矛盾.因此，{un}在E上有界.

定理1.1的證明由引理2.2，命題3.1和命題3.2可得：存在c≥α，序列{un}?E，滿足

φ(un)→c>0，‖φ′(un)‖(1+‖un‖2)→0.

(15)

從而‖φ′(un)‖→0，且‖φ′(un)‖‖un‖→0，故〈φ′(un)，un〉→0.因此，由命題3.3可知{‖un‖}是有界的.從而存在u∈E，使得在E中un?u.因此當n→+∞時，

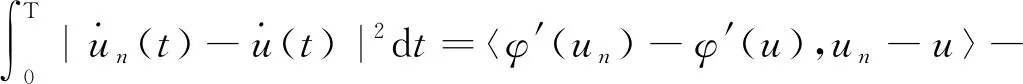
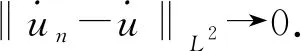
再由引理2.2可知，泛函φ存在一個臨界點u.所以

類似于文獻[15]96頁定理2的證明，在條件(B)，(W1) 和(F)下，u是系統(1)的經典解.

下面證明上述u是非平凡的.反之，存在u(t)≡u0∈Rn，使得

顯然和條件(F)矛盾.因此，系統(1)存在一個非平凡的周期解.

4 例子

例4.1定義G：R×Rn→R，

令

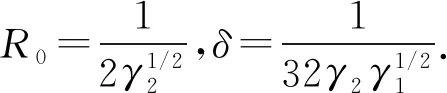
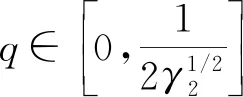
定義函數W(t，x)=(1-λ(|x|))|x|4+λ(|x|)G(t，x)，則B∈C2(R，Rn×n)和W∈C2(R×Rn，R)均關于t是2π周期的.取(a，b)=(0，π)，函數B(t)，W(t，x)顯然滿足條件(B)，(W1)，(W2)，(W3).

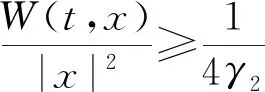
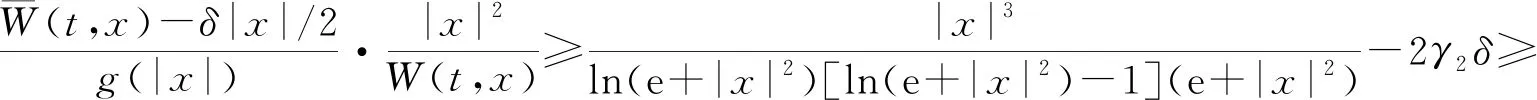
所以函數W(t，x)滿足條件(W4).

令

則

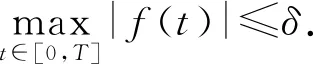
所以函數f(t)滿足條件(F).

因此，上述函數B(t)，W(t，x)和f(t)滿足定理2.1的所有條件.