考慮二次反射條紋的透明被測件多表面干涉測量

常 林，閆恪濤，王 陳，孫 濤，于瀛潔*

（1. 上海大學 機電工程與自動化學院，上海200444；2. 復旦大學 應用經濟學博士后流動站，上海200433；3. 浦發銀行博士后科研工作站，上海200002）

1 引 言

光學表面的精確測量對于量化和評估高精度光學元件具有重要意義［1］。光學干涉測量是一種高精度平面測量方法，其測量精度可以達到納米級［2-3］。隨著測量技術及儀器的發展，多表面透明透鏡的一次性非接觸式測量成為研究熱點。目前，被廣泛應用的測量方式是通過硬件壓電陶瓷干涉儀采集干涉圖，對透明平板非檢測面涂抹消光材料以抑制多表面反射信號，而后經清洗和旋轉，再對另一表面進行測量［4-5］。這種測量方法的缺陷十分明顯：使用硬件干涉儀無法實現多表面干涉信號的特異性區分，即各表面信號的移相值與干涉頻率是相同的，不存在差異性，因此無法通過算法進行區分；其次，被測件表面在涂抹和清洗消光材料時，被測件表面容易造成損傷，因此也無法一次性獲得多表面信號。

De Groot 提出了一種能夠實現單表面干涉圖相位求解的算法，該方法使用不同幀序數下干涉圖的系數加權計算即可得到被測件表面的相位分布信息［6］。Wang 等人發展了一種先進迭代算法，基于最小二乘原理可以計算出被測件干涉信息中的調制度和初始相位等信息，但是沒有考慮多表面干涉情形［7］。Hibino 等人提出一種使用特征多項式根系數分布作為采樣窗，從而進行離散傅里葉變換對目標信號進行提取的移相算法，但是這種算法的采樣窗計算較為復雜，只能使用近似的分段擬合窗函數，并且受采樣定理的限制，此系列算法只能求解固定腔長和厚度相對比值下的干涉信息［8］。

基于波長移相技術的干涉儀和相關算法近年來得到了發展。該技術通過波長可調諧激光器對輸出波長的精確控制進行移相操作，基于不同干涉位置的被測表面在相同波長調諧量的條件下可以實現數值不同的移相，使得各干涉信號具有不同的相移頻率，從而為信號的分離提供基礎。在移相算法中，可應用于多表面干涉測量的主要有兩類，一類是基于離散傅里葉變換的加權多步算法，另外一類是迭代最小二乘算法。加權多步移相算法通過時域加權實現各表面干涉信號的分離，從而獲得初始相位分布，完成表面重建。但是這種算法需要精確地計算干涉頻率，對線性移相的要求較高，當波長調諧線性程度不高時則無法完成相位解調。

本文基于最小二乘原理，提出一種能夠應用于多表面干涉測量的最小二乘迭代算法，并且考慮多次反射條紋，進一步提高求解精度。該算法在處理多表面干涉條紋時能夠獲得精確結果，并且通過實驗系統的搭建進一步驗證了它在實際測量過程中的有效性。

2 干涉測量原理

2.1 多表面干涉測量原理

使用波長移相干涉儀對多表面被測件進行測量時，因為各被測表面與參考面之間的光程差不同，各表面的干涉頻率是不同的，并且可以量化分析。通過移相算法求解出干涉信號中的初始相位，可以重建各被測面的形貌分布［9］。通過干涉儀采集的干涉圖中，各表面所反射的信號會重疊地分布在條紋圖中，因此使用傳統算法直接對條紋圖進行分離是不可能的，必須根據各干涉條紋之間不同的干涉頻率進行信號分離，從而得到目標信號的初始相位等關鍵信息。以單表面干涉為例，每一個像素點的光強照度可以表示為：

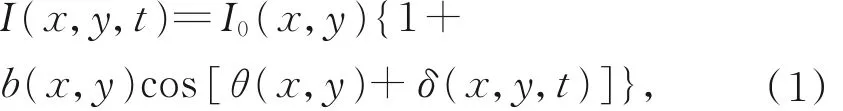
其中 δ ( x，y，t )為干涉圖在t 時刻的移相值。干涉光強I ( x，y，t ) 可以利用CCD 相機采集，移相步長通常作為已知或可測得的主動控制變量，式（1）中只有I0(x，y)，b(x，y)，θ(x，y)（分別對應干涉光強、調制度和初始相位）3 個未知數，故理論上需要采集3 幅或者3 幅以上的干涉條紋圖即可求 出 待 測 表 面 的 初 始 相 位 。 其 中δ(x，y，t)=2πvi(x，y)t，vi為移相頻率，該頻率與其光程差有關［10］。

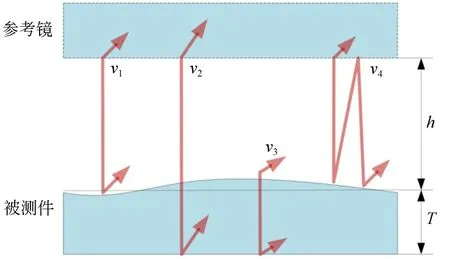
圖1 多表面檢測信號頻率示意圖Fig. 1 Frequency diagram of multi-surface signals

在圖1 中，vi(x，y) 中i=1，2，3，4，分別代表前表面信號、后表面信號、厚度變化信號和二次反射信號（寄生條紋）；T代表被測件的平均厚度，h代表前表面到達參考鏡之間的距離，數值上等同于干涉腔長。使用最小二乘迭代多算法時，通常忽略二次反射信號，本文將次信號納入求解，以提高求解精度。

2.2 最小二乘迭代移相算法

通過干涉儀對多表面透明平行平板進行形貌測量時，各表面信息與參考面之間均會產生干涉。與此同時，基于傳統的計算方法，如果要進一步精確地分析各干涉信息的具體組成和恢復表面形貌，必須考慮寄生條紋對于計算結果的影響。

基于上述分析，本文基于最小二乘法提取各表面的干涉信息，并且分析各誤差對于分離結果的影響。在工業CCD 相機采集到的干涉圖中，不僅存在各干涉信息混疊的復雜信號，還有背景光強和系統采集和處理過程中引入的噪聲。本文通過移相過程中的每一幀減去第一幀的方法進行降噪，目的在于最大程度地減少噪聲信息對結果的影響［11］。考慮多表面干涉混合信息，得到的各點光強如下：

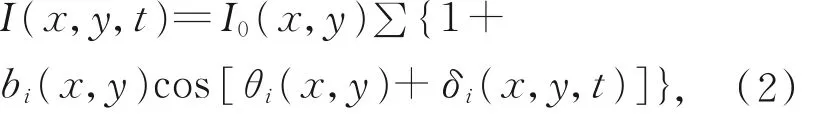
其中i=1，2，3，4，在此分別表示前表面、后表面、厚度以及寄生條紋干涉信息。

使用波長移相干涉儀進行移相操作時，通過改變激光波長達到相位變化的目的。當波長發生改變時，相應的相位變化可以通過對波長變化進行表示，仍以厚度變化信號為例，其第k幀的總相位值以σ1(k) 表示，為簡化描述，坐標不再列出。

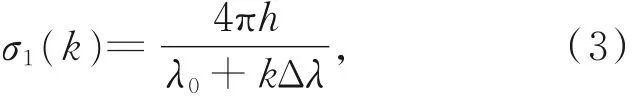
式中：λ0為起始調諧波長，Δλ為單次波長調諧量。移相時波長發生線性變化，相位的變化呈現非線性。對式（3）進行泰勒級數展開可得：

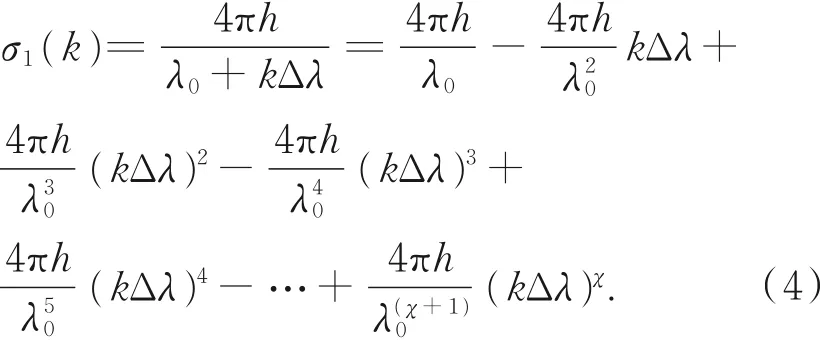
式（4）中，χ進行泰勒展開的最高冪次，k次移相后，相位的變化量為：

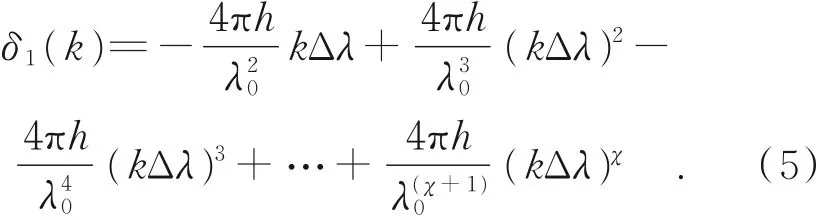
根據式（5）可以量化分析移相過程中的非線性誤差。 當起始調節波長λ0= 632.8 nm，腔長h= 0.1 m，波長調諧量Δλ= 10-4nm。若移相值第一項δ1(k)≈π/2，則第二項的移相值是第一項移相值的kΔλ/λ0≈1.58 × 10-7k倍，也就是說第二項非線性移相遠小于第一項的值，因此測量時忽略第二項及更高次項。 那么式（4）可以改寫為：

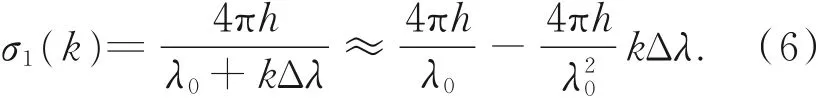
以上即為波長移相干涉技術的相位調諧原理。由于澤尼克多項式和光學檢測中觀測到的像差多項式的形式是相近的，因而常用它來描述波前特性［5-6］。

在實際測量時，需要精確求取前表面、后表面和厚度的變化，從而重建和表征前后表面的形貌分布和厚度均勻性等參數。此處的厚度變化信號指的是被測件前后表面上，去除被測件的平均厚度T 后，一束平行光所穿過的前后兩點之間的距離。因此，通過算法重建的前表面、后表面和厚度變化的微觀分布均可被視作平面大小與被測件表面相同而厚度很薄的微元。本文使用的計算方法所求取的二次反射信號在實際干涉波面重建中的作用是有限的，但是可以通過將該信號從其他信號中進行剝離，來進一步提高前后表面和厚度變化信號的求解精度。

當考慮被測件的多表面干涉信息對于結果的影響時，應當精確分析被測面之間多次反射的寄生信號。此處主要考慮在材料表面二次反射光束與參考面反射光束形成的干涉信號。基于最小二乘原理構建如下方程［12］：

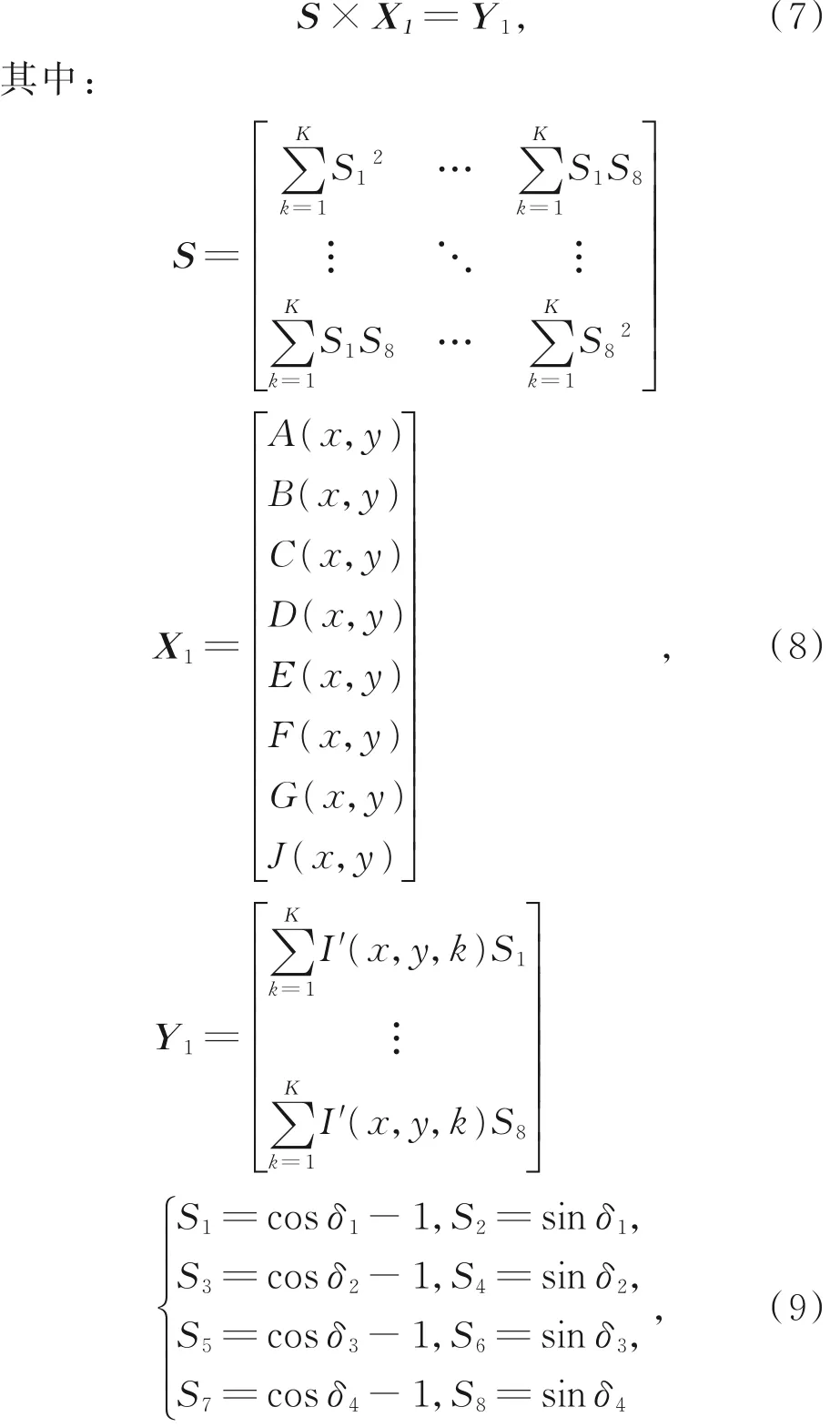
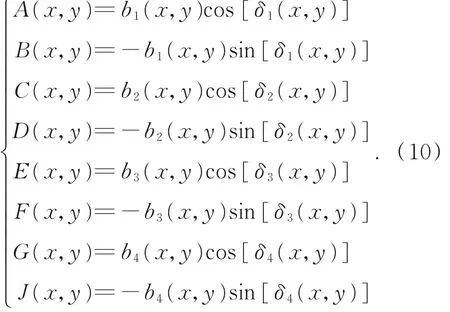
在進行移相時，需要考慮所使用的干涉儀的最大調諧范圍以及采樣點的分布，理論上可以通過減小移相值和增加采集幀數來提高求解精度。但是與此同時，更小的移相步距意味著對波長調諧激光器的調諧精度要求更高，更多的采集幀數會提高測量成本和增加采集過程中納入誤差的可能性，因此需要謹慎選取移相值。基于采樣定理分析，選取的移相值應當大于等于π/2，此時基頻信號滿足香農定理。在初始值的選取方面，如果所選取的初始值與真實值之間的偏離過大，則會致使計算精度降低，甚至導致算法失效。因此在預估移相值的初始值時，使用腔長值（h）和被測件的光學厚度（n1T，n1為被測件的材料折射率）對移相值進行估計，當基頻信號的移相值為π/2時，則根據光程關系，前表面信號為( h/n1T ) π/2，后表面信號為( h/n1T + 1 ) π/2。

按照式（7）～（10）的迭代計算方法，設定移相值為π/5，考慮計算精度和實現成本，迭代次數（也即干涉圖幀數）設為21，通過澤尼克多項式模擬波面，充分考慮寄生條紋對于多表面干涉系統的影響，得到的初始干涉條紋如圖2 所示。

圖2 包含寄生條紋的初始干涉圖Fig. 2 Initial interferogram with parasitic fringes

為了分析寄生條紋對整體計算結果的影響，本文首先使用不考慮寄生條紋的原始計算方法對上述包含多表面干涉信息的模型進行計算（即省去包含寄生項的部分），解相結果如圖3 所示。

圖3 原始算法的分離結果Fig. 3 Separation result of original algorithm

從圖3 可以看出，原始算法的解相結果較差。為了更好地分析解相結果，原始分離算法得到的復原值與真值的殘余誤差如圖4 所示。

通過圖4 可以看出，原始算法的誤差較大。因此，對存在寄生條紋的干涉系統進行精確檢測時，必須考慮寄生項。 本文基于移相值的精確計算，提出最小二乘的拓展計算方法，考慮寄生條紋的光程與腔長的關系，將移相系數與光程差相聯系，納入算法的設計過程以后，再次計算式（7）～式（10），可以得到各干涉信號的解相結果，如圖5 所示。

圖4 原始算法分離結果的殘差Fig. 4 Residual of separation result of original algorithm

圖5 考慮寄生條紋的算法分離結果Fig. 5 Separated results of algorithm considering parasitic fringes

通過上述計算，各信號的殘余誤差如圖6所示。

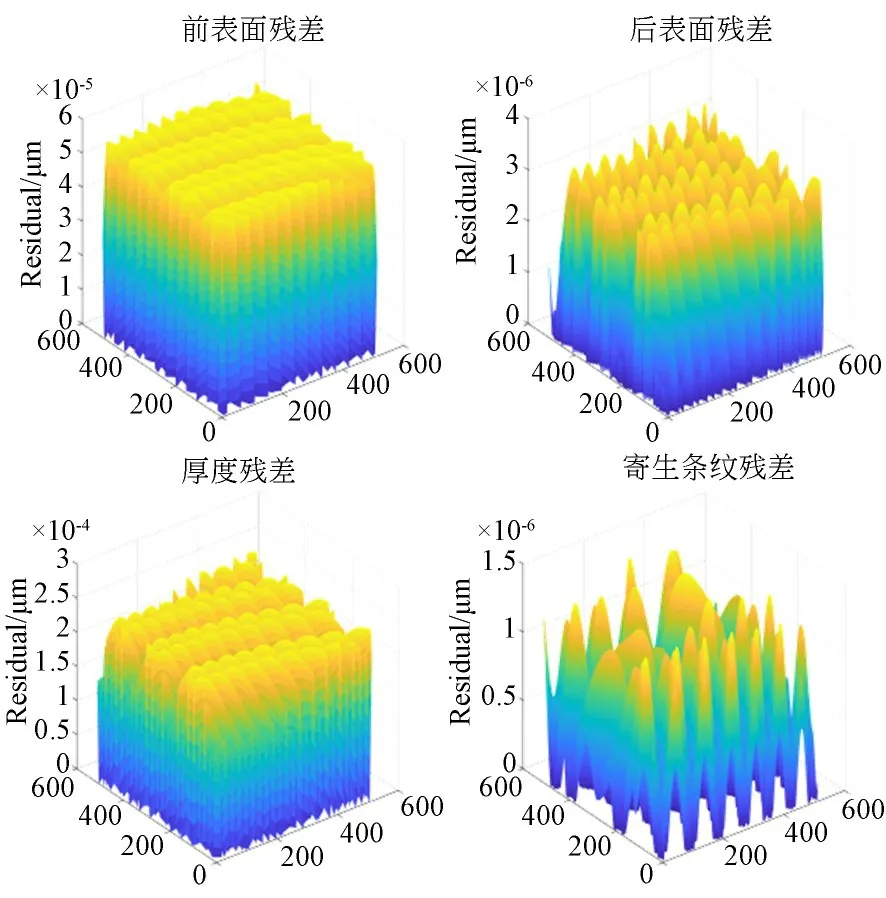
圖6 考慮寄生條紋的算法殘余誤差Fig. 6 Residual errors of algorithm considering parasitic fringes

通過如圖6 所示的殘余誤差結果可以明顯地看到算法分離結果具有很高的精度。由此可知：基于傳統算法分析，在不考慮寄生條紋的情況下對多表面干涉系統進行解相和恢復，結果誤差較大，不能很好地分離各表面信息。若綜合考慮移相值和各表面光程系數的不同，把寄生條紋對算法結果的影響納入算法設計中，可以得到較為精確的測量結果，能夠很好地解相和分離各干涉信號，證明了所設計的算法的有效性。

為充分考量所述算法的魯棒性和適用范圍，本文對所述算法在不同移相值以及不同移相誤差下的結果進行了分析。移相值對于移相算法而言是至關重要的，決定著算法精度，因此應當綜合考慮移相值設定對于結果的影響。將不同的移相值帶入算法設計過程并且進行循環迭代，取各結果的解相均方根值（Root Mean Square，RMS）作為觀察值，如圖7 所示。

圖7 不同移相值下的RMS 結果Fig. 7 RMS results under different phase shift values

在干涉儀實際工作過程中，由于環境的誤差以及激光器本身誤差的存在，移相值并非每一步都符合設計值，因此若綜合判定算法的魯棒性，應當觀察存在移相誤差時算法的結果。以厚度變換信號為例，當被測板較薄時，該信號被選取為基頻信號，其他干涉信號均可以用該信號的不同頻次來表示。 定義移相值的一階誤差如下：

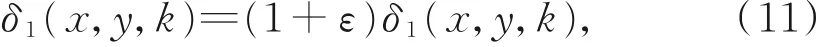
其中：ε是一階移相誤差，δ1(x，y，k)是第k次的設定基礎頻率信號的移相值。將式（11）帶入迭代過程，計算解相結果的RMS 分布如圖8 所示。

分析結果可知，所述最小二乘算法綜合考慮了二次反射寄生條紋對于結果的影響，能夠準確地解相以及提取多表面干涉信息，可以精確、完整地恢復樣品表面形貌，滿足高精度測量需求。同時，所述算法對于移相誤差具有較好的魯棒性，能夠很好地應用于移相誤差較大的情形，進一步證明了該算法的有效性。

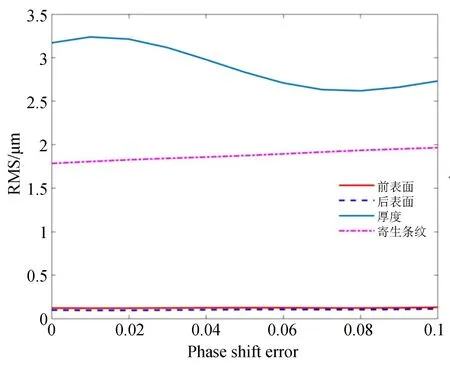
圖8 不同移相誤差下的RMS 結果Fig. 8 RMS results under different phase shift errors

3 實 驗

為驗證所述算法的有效性，實驗使用Fizeau干涉儀和New port 激光器，干涉儀原理如圖9所示。

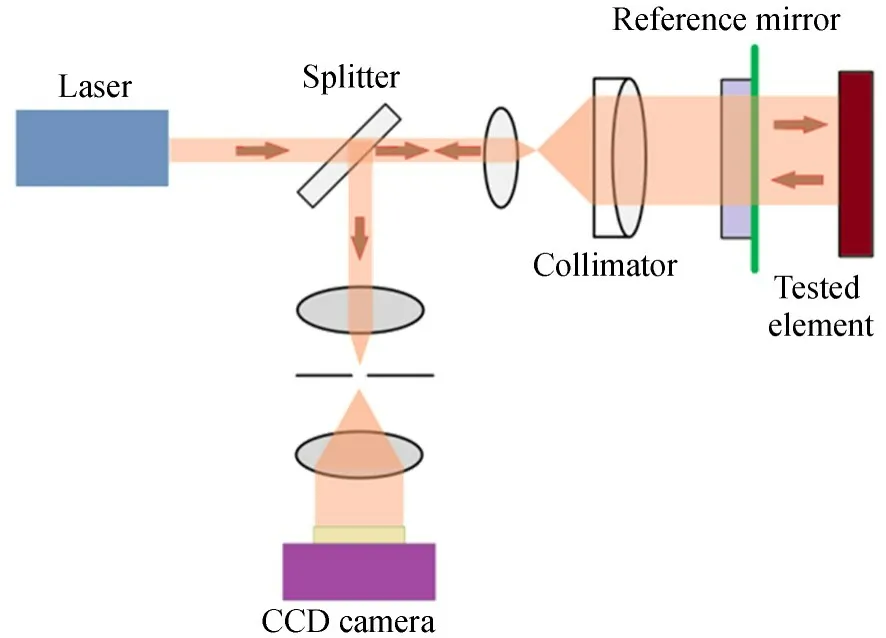
圖9 波長移相干涉儀原理Fig. 9 Schematic diagram of wavelength phase-shift interferometer

使用上述干涉儀與激光器，被測件的平均厚度T=10 mm、折射率n1=1. 52，腔長h=145 mm，中心波長為632. 8 nm，移相步距為π/2，移相總步數為21，計算結果如圖10 所示。

圖10 初始干涉圖和最小二乘算法的解相結果Fig. 10 Initial interferogram and calculated results of least square algorithm

通過上述結果可以看出，基于最小二乘原理的解相算法可以得到精確的解相結果，并且能夠準確地求取寄生條紋，將傳統算法中（包括加權多步算法）被隱藏的二次反射寄生項進行準確提取，該算法不受腔長分布的限制，可以實現任意腔長下的測量。但是也應注意，該算法需要對誤差進行綜合分析和抑制，其計算難度主要在于初始值的選取，若初始值選取不當則得不到精確結果。

4 結 論

本文闡述了基于最小二乘的多表面干涉信息提取算法，在該算法的設計過程中，考慮前表面二次反射信號，并且對比了原始算法及改進算法的計算結果和精度，分析了在不同的移相值和移相誤差下的最小二乘算法RMS 值。 結果表明，所述算法對移相誤差具有較好的魯棒性，可以應對高精度測量情形。考慮二次反射信號的迭代最小二乘算法的理論精度可以達到0. 3 nm，但是當在同等條件下不考慮二次反射信號時，其理論精度為10 nm，并且通過實測數據求解得到的初始相位分布清晰，無雜波干擾，分離結果較為準確。

傳統加權多步采樣算法的特點在于：能夠根據各信號分布的頻率不同從而進行時域傅里葉采樣，算法實現過程較為便捷，但是要符合一定的腔長系數條件，否則無法實現分離。而最小二乘算法則不需要嚴格地遵守腔長系數設置條件，可以在任意腔長下進行測量，但是初始值的預估對結果的影響較大，并且計算量較大，若初始值預估不精確則解相不一定收斂。 因此，根據實驗條件和測量要求的不同，要綜合考慮當前測量條件、誤差和精度，選擇合適的算法及測量方案。