顱面的徑向曲線統計復原模型

王 琳，趙俊莉*，黃瑞坤，李淑嫻，李守哲

（1. 青島大學 數據科學與軟件工程學院，山東 青島266071；2. 大連大學 機械工程學院，遼寧 大連116622；3. 威斯康星大學 麥迪遜分校文理學院，美國威斯康星州麥迪遜53706）

1 引 言

利用人的顱骨進行面貌復原是一個古老的課題。在公安法醫學領域，為了更快速地偵破案件，通常需要及時辨別死者的身份，由于尸體遺骨軟組織高度腐爛的情況時有發生，導致死者的容貌難以分辨，為了更高效地鑒定死者的身份，人們開始嘗試依據顱骨來復原死者的面貌.

早期顱面復原技術［1］采用手工復原方法，復原過程復雜，耗費時間長。近年來計算機技術的介入提高了顱面復原的準確性，使得復原結果更加客觀、高效。計算機輔助顱面復原技術可分為兩類：基于軟組織厚度的顱面復原法和統計模型法。前者是以面部軟組織厚度分布規律為前提進行的復原［2-5］。在此種方法下進行的顱面復原，很難做到準確描述顱面形態信息，顱面形態變化的高度復雜性難以得到體現。統計模型的融入通過對大量顱面數據的統計分析，獲取顱骨和相貌特征之間的本質關系，并依據這種關系進行面貌復原，使得顱面復原的效率和準確度得到了顯著提升，已成為顱面復原研究領域較為熱門的關注點［6］。

顱面統計復原方法一般是將顱骨數據和對應的人臉數據作為訓練樣本，采用統計模型的方法對給定的未知顱骨數據來估算面皮數據。Claes 等［7］首次在顱面復原研究中引入統計模型，并使用稠密點表示的面貌和52 個稀疏特征點表示的顱骨建立主成分分析（Pricinple Component Analysis，PCA）統計模型。Berar 等人［8］采用類似的統計模型建立了稀疏網格表示的顱面變形模型。Hu［9］等人提出了層次化統計模型，采用稠密點云來表示面皮和顱骨數據。 Zhang 等［10］將顱骨、面皮模型按照生理結構進行區域劃分，以分區為單位進行PCA 統計復原，融合后得到誤差較小的復原面貌。Berar 等人［11］利用稀疏網格來表示顱骨和面皮數據，并通過構建顱骨特征點到面皮的回歸模型來完成復原。Duan 等人［12-13］提出了面貌對顱骨的層次化回歸模型來實現面貌復原，且回歸模型構建過程中融合了偏最小二乘回歸的方法，建模效率獲得進一步提高。Madsen［14］等人創建了一個聯合面部形狀模型、顱骨形狀模型和軟組織厚度標記信息的概率模型來獲得給定頭骨形狀的合理面部形狀分布。在這些方法中，采用全部數據稠密點的顱面樣本計算量大，而手工標記特征點又費時費力且不準確；而且顱面形態復雜，生理特征點確定困難；因此如何自動選擇用于統計復原模型的特征點［15］是該方法的關鍵。

本文依據顱面形態的幾何結構，將顱面用一組從鼻尖出發的徑向曲線表示，使用顱骨和人臉面皮上提取的徑向曲線作為訓練樣本數據，構建了一種基于徑向曲線自動定位顱面特征點的顱面統計復原模型，可以減少模型中樣本數據的維度，提高顱面復原的精度和速度。

2 顱面的徑向曲線表示

依據顱面形態的幾何結構，徑向曲線由顱面對稱面和顱面表面的交點來確定。我們提取以鼻尖點為源點且均勻分布于人臉的徑向曲線［16］來表示顱面。

2.1 定位鼻尖點

鼻尖是人臉顯著的生理特征點，因而本文以鼻尖點作為源點，求取鼻尖點與顱面邊界等分點間的徑向曲線。在經過預處理統一坐標系后的標準姿態下的顱面模型，坐標軸Y 方向指向人臉外側，因此由Y 軸方向坐標值最大的點即可確定鼻尖點。如圖1（a）所示。

2.2 估計顱面對稱面

為了減少噪聲造成的影響并提高準確度，在估計顱面對稱面時，首先在經過標準化的目標顱面上取以鼻尖點作為球心、距鼻尖點距離為R =0.5 的球形區域內的點作為顱面裁剪區域FM。然后，以坐標系平面YOZ 為鏡像平面，求得FM的鏡像模型。接著以鼻尖點為標準點將鏡像模型對齊到FM，由FM和組成的新的點云集合可表示為：，其中-F 是一個自對稱模型，FM和FmM對應的平分線就是三維顱面模型的對稱面所在的平面。點集-F 中qi與qmi是左右臉的對稱點，-F 中可以得到N 對對稱點，利用這N對對稱點，采用最小二乘擬合的方法求取顱面對稱面，如圖1（b）所示。

2.3 計算徑向曲線

接下來通過顱面對稱面與顱面網格模型的交點計算第一條徑向曲線如圖1（c）所示，將顱面對 稱 面 繞 軸 線L0逐 次 旋 轉（180/m）°（0° ＜180/m ＜180°）即可獲取m 條徑向曲線（本文經過實驗取m = 30 條，如圖1（d）所示）。為了得到準確的對應點，需要對徑向曲線進行對齊工作，然后對這些點均勻重采樣，并使用均勻采樣點來表示徑向曲線，這里把每條徑向曲線重采樣點數K 取為200 個點。對每一條徑向曲線完成對齊與重采樣后，即可獲得每個顱面重采樣后的徑向曲 線J 表示為：J ={ A| A1，A2，A3，…，Am}。其中每條徑向曲線Ai( i = 1，2，…，m ) 為K 行3列的矩陣。

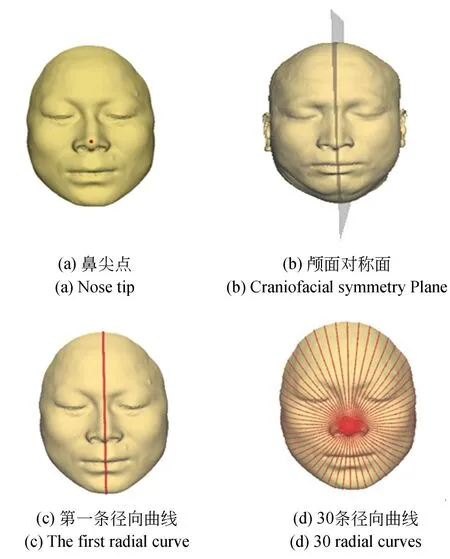
圖1 顱面徑向曲線提取Fig. 1 Extracted radial curves on craniofacial data

3 基于徑向曲線的顱面統計復原

統計模型借助統計的方法分析多樣本數據，并從中認識和學習樣本統計規律，主成分分析（PCA）是最經典的統計模型方法。由于稠密的顱面模型中存在大量噪音數據，本文按如下方法建立基于徑向曲線的顱面統計復原模型。

3.1 復原未知顱骨對應人臉的徑向曲線

本文經過配準后的每個顱骨數據有N 個點，以顱骨和人臉面皮上提取的徑向曲線作為訓練樣本數據，建立基于徑向曲線的統計模型，復原未知顱骨對應人臉的徑向曲線的步驟如下：

（1）建立訓練樣本的顱骨向量：C =[ C1，C2，...，Cn]T；

（2）建立訓練樣本面皮上的徑向曲線向量：J =[ J1，J2，...，Jm]T；

（3）將顱骨向量與面皮上的徑向曲線向量組合建立基于PCA 的統計模型：

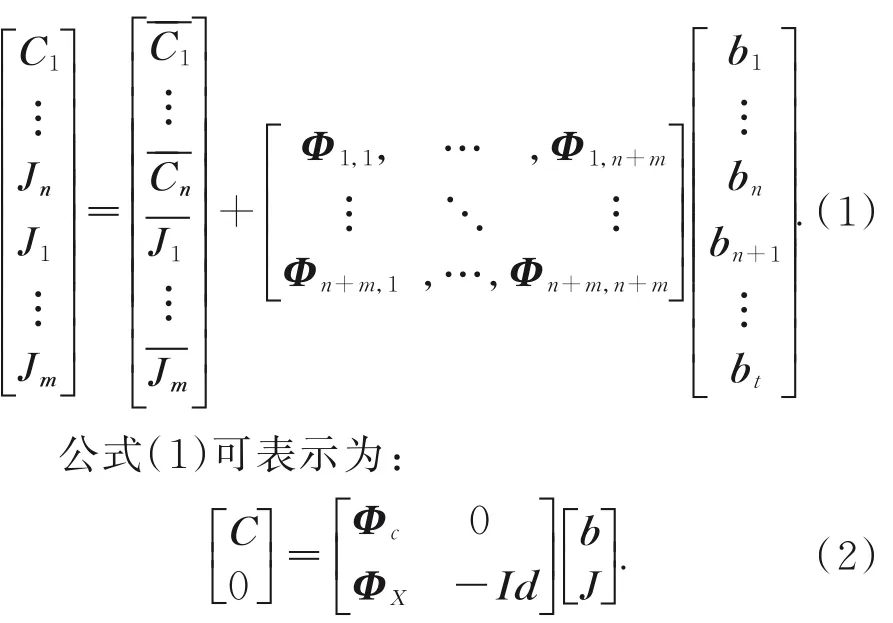
接著，由公式（2）中的部分方程C = Φcb 通過訓練樣本數據可求得到系數b：

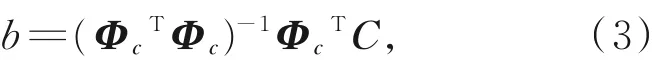
Φ 表示一個矩陣，它的列為協方差矩陣的特征向量，b 表示模型的形狀參數。對于待復原顱骨，將系數b 代入公式（1）后即可求得其對應人臉的徑向曲線。如圖2 所示為復原的一個人臉的徑向曲線。

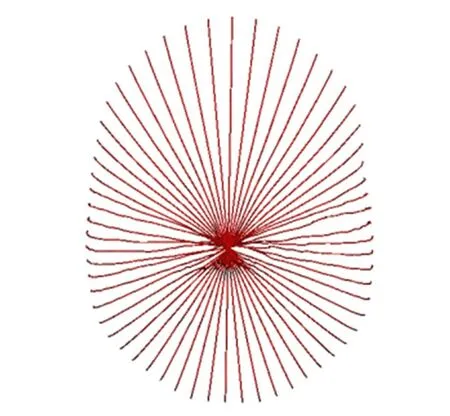
圖2 復原的一個人臉的徑向曲線Fig. 2 Reconstructed radial curves of a skin

3.2 利用復原出的徑向曲線估計人臉

3.2.1 建立人臉統計模型

統計模型通過學習大量樣本信息，能夠得到對象形狀信息的統計經驗，從而獲取更加精確的三維復雜對象的形狀信息。本文采用PCA 按照如下方式建立人臉統計模型：

將一套人臉的原始數據看作一個樣本向量，記 為，1≤i≤N，對于N個人臉樣本向量，首先計算其協方差矩陣：

接下來求CF的特征值和特征向量，將特征值按照降序排列，取前m個最大的特征值λ=(λ1，λ2，…，λm) 和 對 應 的 特 征 向 量U =(U1，U2，...，Um)。

hi代表樣本向量的主分量，可以由以下線性組合表示：

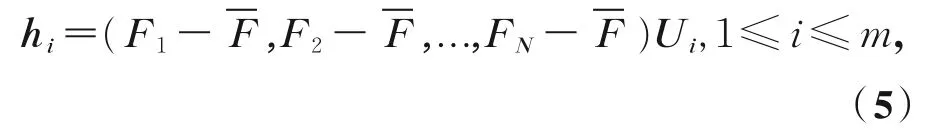
則人臉空間的任一形狀可利用主分量的組合形式近似表示為：

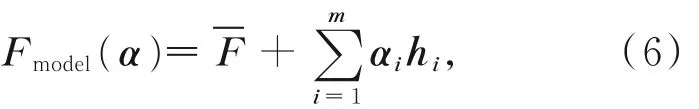
其中：α =(α1，α2，...，αm)為模型參數，同時αi服從高斯分布。在該模型中，參數α取不同的值可以得到不同的人臉。

3.2.2 由徑向曲線估計人臉

建立人臉模型后，本文通過復原出的徑向曲線估計人臉統計模型參數α，進而估計出待復原顱骨對應的面貌。為了使得基于徑向曲線的顱面復原效果達到最好的狀態，需要不斷調整模型參數α，以盡量縮小由徑向曲線估計出的模型與統 計 模 型 之 間 的 誤 差 ，即 最 小 化min‖‖Fmodel(α)-F*，F*表示根據徑向曲線復原出的模型。具體過程如下：

首先，設α初值為0，此時Fmodel(α)= -F，然后利用迭代最近點（ICP）算法確定模型Fmodel(α)中與復原出的徑向曲線J對應的點J′。

接下來由徑向曲線即可估計統計模型參數α：令J - J′= hg α，其中hg表示hi中與徑向曲線點對應的分量，通過最小二乘法可求得α =(hgThg)-1hgT(J′- J)。

新 的 系 數α確 定 后 ，人 臉 模 型Fmodel(α) 便 得以重新計算。迭代上述步驟，使模型之間的誤差達到最小的狀態，以此求得待復原的人臉模型。

4 實驗結果與討論

4.1 實驗數據獲取與預處理

本文用到的顱面數據來自教育部虛擬現實應用工程研究中心建立的顱面數據庫，包括192套完整的顱骨和面皮數據，由螺旋CT 掃描儀對年齡在19～75 歲志愿者的頭部掃描采集得到。首先，從原始CT 切片圖像中提取出顱面輪廓，并使用Marching Cubes 算法［17］完成顱面 的三維建模。然后將所有三維顱面數據統一至法蘭克福坐標系下［18-19］，以消除不同姿態等因素的影響。由于整個顱面的頂點過多，且面部特征主要集中在頭部的前面部分，因此本文選擇一組顱面數據作為參考模板，將其后面部分切除。最后，將所有顱面模型通過TPS（Thin Plate Spline）非剛性配準方法［9，20］進行配準，配準后每個顱骨和面皮數據分別包含41 059 和40 969 個頂點。

4.2 復原精度對比

對上述192 套顱面數據，分別采用本文提出的基于徑向曲線的顱面統計復原方法和經典的PCA 統計復原方法進行實驗。實驗采用留一法［21］，即把192 套中的1 套用來測試，另外191 套用來訓練，依次循環，復原出相應的192 個人臉，與原始面貌進行對比，利用歐式距離計算出誤差。兩種復原方法的復原結果如下表1 所示，誤差圖中藍色表示誤差為0，紅色表示誤差最大（彩圖見期刊電子版）。可看出基于徑向曲線的顱面復原效果更好，復原出的面貌與原始面貌更接近。

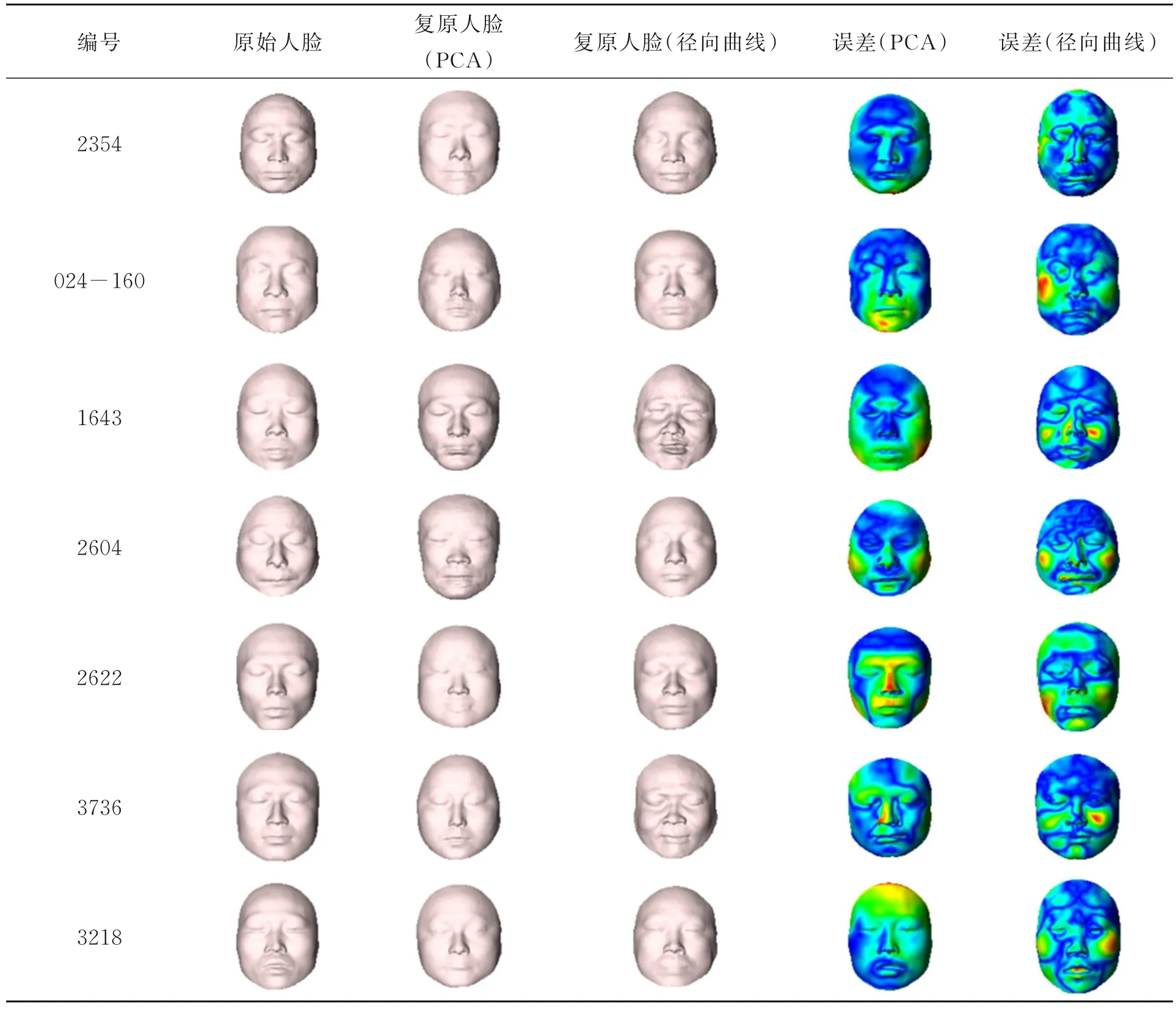
表1 復原結果比較Tab. 1 Comparison of reconstructed results

對于192 套測試樣本在兩種復原方法下得到的復原人臉，分別計算其與對應的原始人臉之間的距離誤差，包括最小值、平均值、最大值、方差4種指標，并最終求出192 個復原人臉各項距離誤差對應的均值，如表2 所示。顯然本文方法的各項平均距離誤差均顯著小于PCA 復原誤差。

表2 統計距離誤差的平均值Tab. 2 Average statistical distance error

為了更直觀地展示實驗結果，本文用折線圖表示192 套測試樣本對應的原始人臉與復原人臉的距離誤差，如圖3 所示，圖中橫坐標軸表示樣本編號（間隔為10），縱坐標軸表示原始人臉與復原人臉的距離誤差，很明顯基于徑向曲線的復原結果（綠色折線）與原始人臉的距離誤差比PCA 復原結果（藍色折線）更小，復原效果更好（彩圖見期刊電子版）。

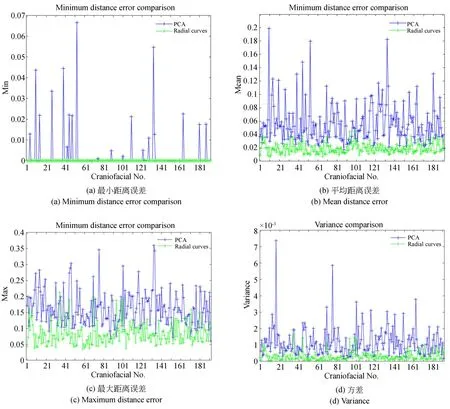
圖3 原始人臉與復原人臉統計距離誤差Fig. 3 Statistical distance error between original faces and reconstructed faces

4.3 復原速度對比

在復原速度方面，本文逐個對每個復原人臉分別用本文方法和PCA 顱面統計復原方法的復原時間進行統計，用直觀的折線圖表示，如圖4 所示；并分別計算兩類方法下192 個人臉復原時間的平均值，結果如表3 所示。圖4 橫坐標軸表示樣本編號（間隔為10），縱坐標軸表示單個樣本完成復原耗費的時間，可以觀察到本文方法（綠色折線）所用的每個人臉的復原時間均短于PCA 顱面統計復原（藍色折線）所用的時間（彩圖見期刊電子版）。這是由于采用本文提出的徑向曲線進行復原時，徑向曲線的點數遠少于進行PCA 統計復原時采用的顱面全部數據的點數，因而本文方法人臉復原耗費的時間更短，即基于徑向曲線的顱面復原速度更快。表3 和圖4 從復原速度的角度驗證了本文方法要優于PCA 顱面統計復原效率。

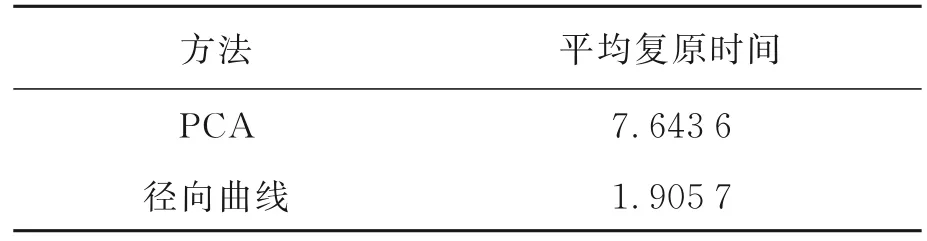
表3 平均復原速度對比Tab. 3 Average reconstructed speed comparison

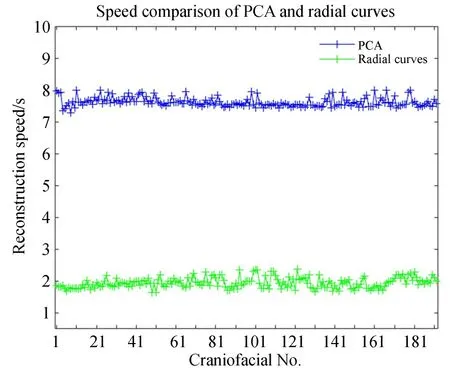
圖4 人臉復原時間對比Fig. 4 Time comparison of reconstructed faces

5 結 論

本文提出了一種新的基于徑向曲線的顱面統計復原模型，在三維顱面模型上提取了以鼻尖點為起點的均勻分布于人臉的徑向曲線作為顱面表示，自動定位顱面幾何特征點，以顱骨和人臉面皮上提取的徑向曲線建立顱面統計復原模型，采用留一法對192 套顱面數據進行實驗，實驗結果表明：與基于PCA 的顱面復原方法相比，本文提出的基于徑向曲線的顱面統計復原方法的復原精度提高了2. 95 倍，速度提高了4. 01 倍。綜合分析后可以看出基于徑向曲線的顱面復原方法降低了模型中樣本數據的維度，提高了顱面復原的精度和速度，顱面復原的效果得到進一步的改善。本文所提的基于徑向曲線的顱面統計復原方法不僅可以用于顱面復原中，也可用于三維顱骨或人臉的缺失補全等應用中，徑向曲線的表示方法也可用于三維人臉識別、顱骨相似性度量等應用中，對三維模型的分析、修補和識別也具有一定的借鑒意義。