從問題類屬談初中生數(shù)學(xué)建模能力培養(yǎng) ①

孫 凱

(江蘇省蘇州市陽山實驗初級中學(xué)校 215151)

1 問題提出

問題解決能力是21世紀(jì)人才應(yīng)具備的關(guān)鍵能力之一.數(shù)學(xué)建模作為連接數(shù)學(xué)與外部世界的橋梁，是將現(xiàn)實世界中的實際問題轉(zhuǎn)化為數(shù)學(xué)問題并用數(shù)學(xué)的知識解決問題的活動過程.進(jìn)入21世紀(jì)，數(shù)學(xué)教育發(fā)達(dá)國家的數(shù)學(xué)課程改革都尤為注重數(shù)學(xué)建模能力的培養(yǎng)，并將其作為最重要的數(shù)學(xué)教育目標(biāo).在我國初中數(shù)學(xué)教學(xué)中，提到數(shù)學(xué)建模教學(xué)，廣大一線教師最先想到的是方程模型、不等式模型、函數(shù)模型，進(jìn)一步還能想到幾何模型、概率模型等，大部分教師認(rèn)為運用這些數(shù)學(xué)模型解決問題(應(yīng)用題)就是數(shù)學(xué)建模，甚至將應(yīng)用題教學(xué)與數(shù)學(xué)建模教學(xué)畫上等號，認(rèn)為落實好應(yīng)用題教學(xué)就是培養(yǎng)學(xué)生的數(shù)學(xué)建模能力.顯然，這種觀點是對初中數(shù)學(xué)建模教學(xué)尤其是數(shù)學(xué)建模內(nèi)容的片面認(rèn)識，對數(shù)學(xué)建模教學(xué)構(gòu)成了一定的負(fù)面影響，阻礙了初中學(xué)生數(shù)學(xué)建模能力的有效培養(yǎng).

2 對初中生數(shù)學(xué)建模能力的認(rèn)識

2.1 數(shù)學(xué)建模的內(nèi)涵

什么是數(shù)學(xué)建模？數(shù)學(xué)建模就是通過建立模型的方法來求得問題解決的數(shù)學(xué)活動過程[1].從數(shù)學(xué)與現(xiàn)實世界的關(guān)系上看，數(shù)學(xué)建模就是將現(xiàn)實世界中的實際問題轉(zhuǎn)化為數(shù)學(xué)問題并用數(shù)學(xué)的知識解決問題(如圖1).這種從數(shù)學(xué)之外領(lǐng)域開始，移動到數(shù)學(xué)領(lǐng)域?qū)で蟠鸢福@得數(shù)學(xué)的結(jié)論并翻譯到數(shù)學(xué)之外領(lǐng)域的過程叫做數(shù)學(xué)建模[2].數(shù)學(xué)建模目的是利用形式化的數(shù)學(xué)模型去反映(模寫、刻畫、表征)現(xiàn)實系統(tǒng)中的關(guān)系結(jié)構(gòu)(關(guān)系——映射)，然后利用通過對模型的邏輯分析演繹得出的結(jié)論，把它反演(翻譯)回去解答現(xiàn)實原型中的某些問題(反演)[3].“數(shù)學(xué)建模”中的“數(shù)學(xué)”具有多重含義，其首要含義是指數(shù)學(xué)化，即將現(xiàn)實世界的實際問題抽象、簡化、假設(shè)、提煉轉(zhuǎn)化為數(shù)學(xué)問題，最終實現(xiàn)把外部世界的問題轉(zhuǎn)入數(shù)學(xué)內(nèi)部解決.“數(shù)學(xué)建模”中的“建模”是指建構(gòu)數(shù)學(xué)模型，數(shù)學(xué)模型是指反映特定問題或特定事物的系統(tǒng)特征或相互依賴的關(guān)系，運用形式化的數(shù)學(xué)語言，抽象、概括、近似地表達(dá)而形成的一種穩(wěn)定的、系統(tǒng)的數(shù)學(xué)結(jié)構(gòu).從廣義上看，初中數(shù)學(xué)教學(xué)上的數(shù)學(xué)概念、理論體系、公式、定理、算法系統(tǒng)等都屬于數(shù)學(xué)模型；而狹義的數(shù)學(xué)模型是指反映特定問題或特定事物的數(shù)學(xué)結(jié)構(gòu).

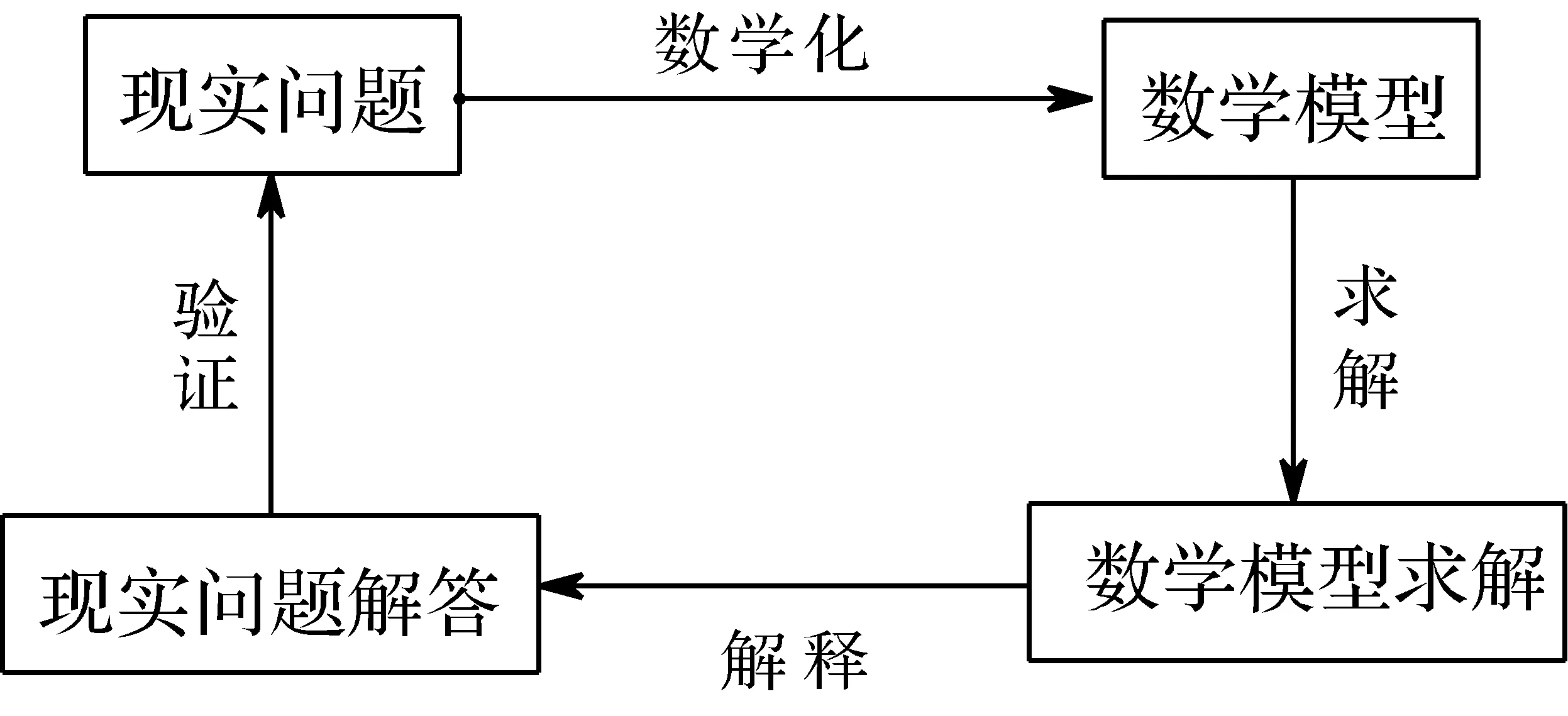
圖1 建模循環(huán)模型

2.2 初中生數(shù)學(xué)建模的內(nèi)容

從數(shù)學(xué)建模內(nèi)容維度來看，初中生數(shù)學(xué)建模所面對的現(xiàn)實問題一般分為三類：現(xiàn)實原型、實際模型、數(shù)學(xué)形式.這種從數(shù)學(xué)建模內(nèi)容視角對現(xiàn)實問題的分類就是“問題類屬”.現(xiàn)實世界中初看起來雜亂無章的生活現(xiàn)象，真實的實際問題，屬于現(xiàn)實原型；將現(xiàn)實原型進(jìn)行修改和簡化，形成一種比較精確和簡潔的表達(dá)，這時可稱之為一個實際模型[4](也稱為“現(xiàn)實模型”)；將實際模型進(jìn)一步簡化、假設(shè)，用數(shù)學(xué)符號表達(dá)實際模型中的變量和關(guān)系，形成數(shù)學(xué)形式，得到的結(jié)果就是一個數(shù)學(xué)模型.數(shù)學(xué)建模的最關(guān)鍵環(huán)節(jié)是“現(xiàn)實原型—實際模型—數(shù)學(xué)形式”這一子過程.

初中數(shù)學(xué)教材中呈現(xiàn)的實際問題(以下簡稱“應(yīng)用題”)是教材編寫者進(jìn)行一定的抽象、簡化、假設(shè)后的問題情境，屬于實際模型類問題.這類問題是既定的數(shù)學(xué)形式化結(jié)構(gòu)披上了一層現(xiàn)實世界的外衣，是一種標(biāo)準(zhǔn)數(shù)學(xué)模型的回譯，表現(xiàn)為從數(shù)學(xué)知識往外看(現(xiàn)實世界).而真正的數(shù)學(xué)建模起始于沒有“編輯”的現(xiàn)實世界，要求在問題解決之前進(jìn)行數(shù)學(xué)表述[5]，表現(xiàn)為從現(xiàn)實世界(現(xiàn)實問題)向內(nèi)看(數(shù)學(xué)問題)，思考運用或創(chuàng)造什么樣的數(shù)學(xué)知識和方法解決實際問題.從過程維度來看，應(yīng)用題教學(xué)是從實際模型到數(shù)學(xué)形式的活動過程，是數(shù)學(xué)建模最關(guān)鍵環(huán)節(jié)中的一個階段，不是完整意義上的數(shù)學(xué)建模教學(xué).事實上，數(shù)學(xué)建模區(qū)別于一般應(yīng)用題的一大特點是對現(xiàn)實問題的抽象假設(shè)，這對于學(xué)生而言是難點，但卻是數(shù)學(xué)建模的重要環(huán)節(jié)[6].初中數(shù)學(xué)教材上的數(shù)學(xué)概念、公式、定理等內(nèi)容一般歸類為數(shù)學(xué)形式類問題，課題學(xué)習(xí)、綜合實踐活動等內(nèi)容歸類為現(xiàn)實原型類問題.

2.3 初中生數(shù)學(xué)建模能力的內(nèi)涵及水平劃分

數(shù)學(xué)建模能力就是將現(xiàn)實問題表述為數(shù)學(xué)形式，并使用數(shù)學(xué)求解，將數(shù)學(xué)結(jié)果轉(zhuǎn)譯為現(xiàn)實結(jié)果并檢驗的能力[7].初中生數(shù)學(xué)建模能力是指初中學(xué)生利用形式化的數(shù)學(xué)模型去反映現(xiàn)實問題中的關(guān)系結(jié)構(gòu)，通過對數(shù)學(xué)模型的求解和檢驗，解答現(xiàn)實原型中某些問題的能力.PISA2012的數(shù)學(xué)測評框架把數(shù)學(xué)化能力當(dāng)作數(shù)學(xué)的一種基本能力來區(qū)分水平[5]288.數(shù)學(xué)化是數(shù)學(xué)建模的最關(guān)鍵成分，數(shù)學(xué)化能力是初中生數(shù)學(xué)建模能力的本質(zhì)和關(guān)鍵.因此，一般按照數(shù)學(xué)建模過程中數(shù)學(xué)化的復(fù)雜程度來劃分?jǐn)?shù)學(xué)建模能力水平.

一個來自現(xiàn)實原型中的實際問題，經(jīng)過數(shù)學(xué)化的過程，呈現(xiàn)為數(shù)學(xué)問題，能否有效建構(gòu)數(shù)學(xué)模型是解決數(shù)學(xué)問題的關(guān)鍵.在初中階段，根據(jù)學(xué)生將現(xiàn)實問題與數(shù)學(xué)形式之間來回轉(zhuǎn)譯的能力，根據(jù)數(shù)學(xué)化的復(fù)雜程度，將初中生數(shù)學(xué)建模水平按從低到高劃分為三個層次：再現(xiàn)、聯(lián)系、反思.再現(xiàn)是指在簡單熟悉的問題情境下，識別出標(biāo)準(zhǔn)模型解決問題，表現(xiàn)為標(biāo)準(zhǔn)數(shù)學(xué)模型的再現(xiàn)；聯(lián)系是指在較綜合的問題情境下，遷移、組合、轉(zhuǎn)化標(biāo)準(zhǔn)模型解決問題，表現(xiàn)為標(biāo)準(zhǔn)數(shù)學(xué)模型的組合與變形；反思是指在復(fù)雜的問題情境下，檢驗、評價、比較、改進(jìn)數(shù)學(xué)模型，表現(xiàn)為數(shù)學(xué)模型的改進(jìn)和創(chuàng)造.

初中數(shù)學(xué)教材上呈現(xiàn)的源于現(xiàn)實世界的應(yīng)用題往往是經(jīng)過教材編寫者抽象、簡化、假設(shè)的問題情境，并不是真實的現(xiàn)實原型，而是實際模型.在這里并非否定教材上諸多實際模型的教學(xué)價值，而是希望廣大初中教師對此有較為清晰的認(rèn)識，以便更好地開展數(shù)學(xué)建模教學(xué).從數(shù)學(xué)建模水平維度來看，初中數(shù)學(xué)教材上呈現(xiàn)的實際模型類問題多屬于再現(xiàn)水平，對初中生更高層次數(shù)學(xué)建模能力的培養(yǎng)以及應(yīng)用意識和創(chuàng)新能力的培養(yǎng)顯得力不從心.因此，在初中數(shù)學(xué)建模教學(xué)中，一方面要以教材上的實際模型類問題為基礎(chǔ)，引導(dǎo)學(xué)生積極參與數(shù)學(xué)建模活動，培養(yǎng)學(xué)生再現(xiàn)水平；另一方面要注重關(guān)聯(lián)或引入現(xiàn)實原型類問題情境，培養(yǎng)學(xué)生聯(lián)系和反思水平.

3 初中生數(shù)學(xué)建模能力次第水平示例

3.1 再現(xiàn)：銷售

一件夾克衫先按成本提高50%標(biāo)價，再以8折出售，獲利28元.這件夾克衫的成本是多少元？

說明這是一道源于現(xiàn)實原型的，以實際模型形式呈現(xiàn)的銷售問題.問題中的成本、標(biāo)價、折扣、售價、獲利等詞匯是學(xué)生分析和解決問題的主要障礙.弄清這些關(guān)鍵詞的意義，準(zhǔn)確理解題意，用數(shù)學(xué)符號表達(dá)售價、成本和利潤，是構(gòu)建一元一次方程模型解決問題的關(guān)鍵.這是一種數(shù)學(xué)標(biāo)準(zhǔn)模型的識別與運用，屬于直接套用，屬于數(shù)學(xué)建模能力再現(xiàn)水平.

3.2 聯(lián)系：方艙

為了應(yīng)對2020年2月在武漢發(fā)生的新型冠狀病毒疫情，國家衛(wèi)健委決定在武漢建立方艙醫(yī)院，其中一所方艙醫(yī)院的具體信息如下：

1.方艙醫(yī)院由四部分組成，分別是醫(yī)療功能單元、病房單元、技術(shù)保險單元、廢棄物處理單元；

2.整個方艙醫(yī)院面積為80000平方米；

3.廢棄物處理單元面積為總面積的5%；

4.病房單元面積是技術(shù)保障單元面積的4倍；

5.病房單元與醫(yī)療功能單元面積的和不高于總面積的85%.

求醫(yī)療功能單元的最大面積.

說明方艙醫(yī)院的建設(shè)問題是源于現(xiàn)實生活的真實問題.問題情境中給出部分信息，學(xué)生需要將現(xiàn)實原型信息進(jìn)一步抽象、假設(shè)、簡化為數(shù)學(xué)問題，用數(shù)學(xué)符號表示病房單元和醫(yī)療功能單元的面積，建構(gòu)一元一次不等式模型解決問題.問題情境中蘊涵方程模型、不等式模型，是數(shù)學(xué)標(biāo)準(zhǔn)模型的遷移、組合，屬于數(shù)學(xué)建模能力聯(lián)系水平.

3.3 反思：節(jié)水

我們常常聽到長輩告訴我們，洗澡時盡量用淋浴的方式，會比較節(jié)水.但事實是如此嗎？若某家庭有兩種可以選擇的洗澡方式，其中一種是泡澡浴缸：長為1.3米，寬為0.7米，高為0.7米的長方體浴缸(內(nèi)部測量)，通常在泡澡時水深為0.5米.另一種為淋浴，利用淋蓬頭沖澡，其中淋蓬頭可以調(diào)整水流速度，分成高速水流和低速水流兩種，高速水流的出水量為15升/分鐘，低速水流的出水量為10升/分鐘[8].若小明選用泡澡方式，而小華選用淋浴方式，問哪種方式比較節(jié)水？

說明洗澡節(jié)水問題是一個復(fù)雜的現(xiàn)實問題情境，考慮到初中生的知識儲備與認(rèn)知水平，對現(xiàn)實問題進(jìn)行了一定的簡化、假設(shè)，情境中給出了一些關(guān)鍵信息.學(xué)生解決這個問題，仍需考慮淋浴時間、水流速度等因素，從實際問題中抽象出數(shù)學(xué)模型或作必要的假設(shè)進(jìn)行探索，并對模型進(jìn)行檢驗、比較、優(yōu)化，屬于數(shù)學(xué)建模能力反思水平.

4 培養(yǎng)初中生數(shù)學(xué)建模能力的教學(xué)策略

4.1 立足教材，掌握標(biāo)準(zhǔn)模型，在實際模型類問題的解決中培養(yǎng)再現(xiàn)水平

模型思想是初中數(shù)學(xué)課程的十大核心概念之一.模型思想的建立是學(xué)生體會和理解數(shù)學(xué)與外部世界聯(lián)系的基本途徑，建立和求解模型的過程包括：從現(xiàn)實生活或具體情境中抽象出數(shù)學(xué)問題，用數(shù)學(xué)符號建立方程、不等式、函數(shù)等表示數(shù)學(xué)問題中的數(shù)量關(guān)系和變化規(guī)律，求出結(jié)果并討論結(jié)果的意義[9]7.為促進(jìn)學(xué)生模型思想的形成，教材編者注重數(shù)學(xué)知識與現(xiàn)實世界的聯(lián)系，在每個章節(jié)中都設(shè)置了應(yīng)用類的實際問題，意在促進(jìn)學(xué)生經(jīng)歷運用數(shù)學(xué)知識解決實際問題的過程，初步形成模型思想，體會數(shù)學(xué)的應(yīng)用價值，提高數(shù)學(xué)學(xué)習(xí)興趣和應(yīng)用意識.從建模教學(xué)內(nèi)容來看，學(xué)生的大部分時間是在學(xué)習(xí)數(shù)學(xué)內(nèi)部的內(nèi)容，比如數(shù)學(xué)概念、性質(zhì)、定理等，這種學(xué)習(xí)可以看作數(shù)學(xué)標(biāo)準(zhǔn)模型的學(xué)習(xí)，最終指向?qū)嶋H問題的解決.從數(shù)學(xué)建模過程來看(如圖2)，以教材為載體的初中數(shù)學(xué)教學(xué)中，用方程、不等式、函數(shù)、圖形、概率等數(shù)學(xué)模型解決實際問題屬于從實際模型到數(shù)學(xué)模型，這類問題情境中的數(shù)學(xué)模型容易識別，直接套用標(biāo)準(zhǔn)模型即可解決，是培養(yǎng)學(xué)生數(shù)學(xué)建模能力再現(xiàn)水平的重要途徑.在實際模型類問題教學(xué)中，應(yīng)引導(dǎo)學(xué)生將實際模型進(jìn)一步抽象化、符號化，經(jīng)歷識模、建模、解模等活動，提高數(shù)學(xué)建模能力的再現(xiàn)水平.

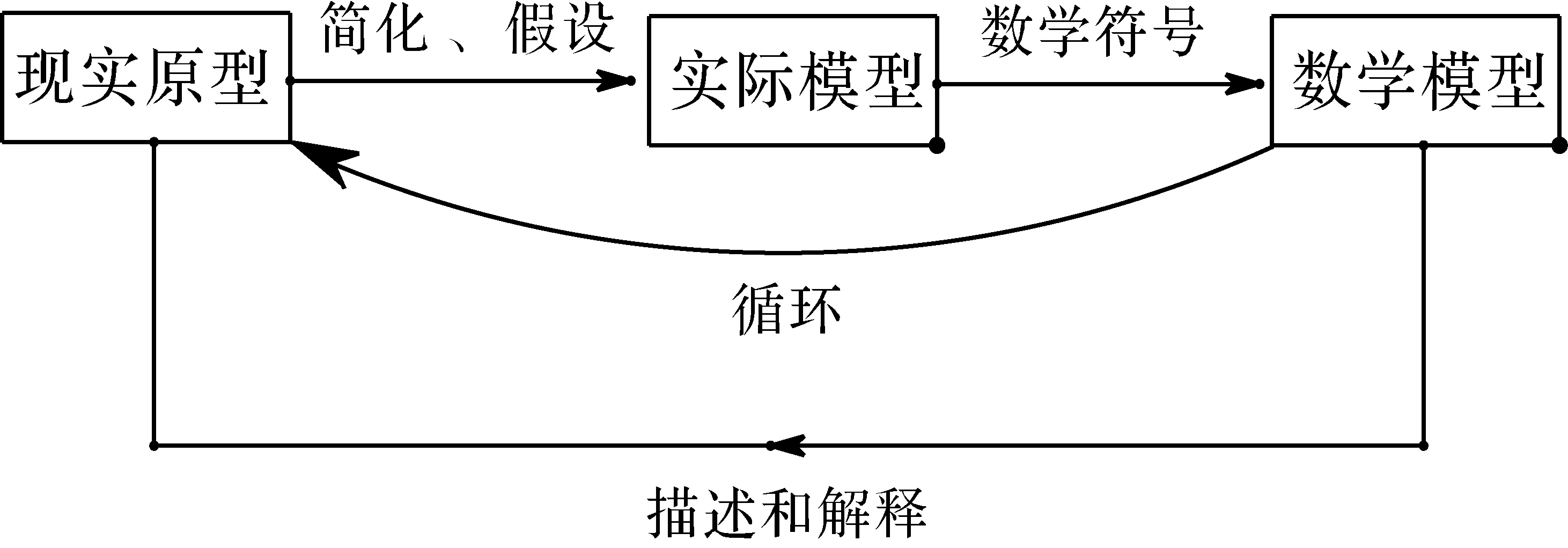
圖2 建模過程

4.2 觀察生活，發(fā)掘現(xiàn)實問題，在現(xiàn)實原型類問題的解決中培養(yǎng)聯(lián)系水平

數(shù)學(xué)學(xué)習(xí)的最終目標(biāo)是讓學(xué)習(xí)者會用數(shù)學(xué)眼光觀察現(xiàn)實世界、會用數(shù)學(xué)思維思考現(xiàn)實世界、會用數(shù)學(xué)語言表達(dá)現(xiàn)實世界.這里所謂的用數(shù)學(xué)語言表達(dá)現(xiàn)實世界其實質(zhì)就是數(shù)學(xué)建模.為彌補教材上實際模型類問題在培養(yǎng)學(xué)生數(shù)學(xué)建模能力聯(lián)系水平上的缺失，教師應(yīng)善于發(fā)掘現(xiàn)實世界中的實際問題，選擇適切的、真實的、綜合的問題情境，使學(xué)生完整經(jīng)歷現(xiàn)實問題——實際模型——數(shù)學(xué)模型——求解結(jié)果——檢驗解釋的建模活動，尤其是將現(xiàn)實問題簡化、假設(shè)、概括后抽象出實際模型的過程，培養(yǎng)學(xué)生將現(xiàn)實問題數(shù)學(xué)化的能力.現(xiàn)實原型類問題初看起來雜亂無序，這就要求教師在教學(xué)時引導(dǎo)學(xué)生精選變量和關(guān)系，保留問題的“主干”，削減問題的“枝杈”，簡化描述，提出合理的假設(shè)，建立相應(yīng)的數(shù)學(xué)模型，并用恰當(dāng)?shù)臄?shù)學(xué)符號表示，最終用數(shù)學(xué)知識解決問題，以培養(yǎng)學(xué)生數(shù)學(xué)建模能力的聯(lián)系水平.比如在“方艙”建模活動中，先由學(xué)生獨立閱讀獲取信息，再自主完成信息的分析、篩選、簡化、假設(shè)，將實際問題進(jìn)一步數(shù)學(xué)化，用數(shù)學(xué)語言正確表達(dá)模型的結(jié)構(gòu)特征以及相互關(guān)系，獲得數(shù)學(xué)模型并解決問題.

4.3 任務(wù)驅(qū)動，聯(lián)系現(xiàn)實世界，在綜合實踐類活動中培養(yǎng)反思水平

“綜合與實踐”是指學(xué)生運用學(xué)習(xí)掌握的數(shù)學(xué)知識、思想和方法解決現(xiàn)實問題，可以理解為數(shù)學(xué)探究和數(shù)學(xué)建模活動.其主要內(nèi)容為：結(jié)合實際情境，經(jīng)歷設(shè)計解決具體問題的方案，并加以實施的過程，體驗建立模型、解決問題的過程[9]41.綜合實踐活動在培養(yǎng)學(xué)生問題意識、應(yīng)用意識、創(chuàng)新意識等方面具有得天獨厚的優(yōu)勢，是培養(yǎng)學(xué)生數(shù)學(xué)建模能力的有效途徑.在初中數(shù)學(xué)教學(xué)中，受考試指揮棒和知識本位等因素影響，廣大一線教師特別注重數(shù)與代數(shù)、圖形與幾何、統(tǒng)計與概率三個部分的教學(xué)，往往忽視或直接放棄課程內(nèi)容中綜合與實踐部分的教學(xué).事實上，綜合與實踐課程內(nèi)容的主要功能是在數(shù)學(xué)與外部世界之間搭建橋梁，是學(xué)生主動運用數(shù)學(xué)知識以及其他學(xué)科知識解決實際問題的重要途徑，也是培養(yǎng)學(xué)生數(shù)學(xué)建模能力的有效路徑.因此，教師應(yīng)充分挖掘教材上綜合與實踐課程內(nèi)容的教學(xué)價值，注重發(fā)掘現(xiàn)實生活中的問題，每個月或每學(xué)期組織開展一次綜合實踐活動，驅(qū)動學(xué)生用數(shù)學(xué)的眼光觀察現(xiàn)實世界，發(fā)現(xiàn)和提出有價值的問題，自主探究、合作交流，動腦、動手、動口，經(jīng)歷建立數(shù)學(xué)模型解決問題的活動過程，使學(xué)生感悟數(shù)學(xué)來源于實踐，又應(yīng)用于實踐[10].比如將上述“節(jié)水”問題進(jìn)一步還原為更“原始”的形態(tài)，將一些數(shù)據(jù)信息剔除，呈現(xiàn)為現(xiàn)實原型問題：“我們常常聽到長輩告訴我們，洗澡時盡量用淋浴的方式，淋浴會比浴缸泡澡更節(jié)水.事實是如此嗎？”對學(xué)生而言，這樣的實際問題就是一種主題綜合實踐活動，解決這個問題需要學(xué)生完成數(shù)據(jù)收集、模型假設(shè)等工作，將實際問題轉(zhuǎn)化為數(shù)學(xué)問題，抽象出數(shù)學(xué)模型進(jìn)行探索，使學(xué)生完整經(jīng)歷引模、建模、解模、驗?zāi)５幕顒舆^程，從而有效培養(yǎng)學(xué)生數(shù)學(xué)建模能力的反思水平.