基于時間差分出租車智能規劃研究

張南楠，童 林，唐倩倩

（1.貴州電子信息職業技術學院，貴州 凱里 556000；2.六盤水師范學院，貴州 六盤水 553004）

引言

針對當前的出租車運輸體系，主要存在如下問題。出租車空載率高。在一些大型城市，例如北京、廣州，每天空駛距離在40%左右[1]。如此高的比例，必然占用了社會道路交通的資源，造成路面擁堵，大氣污染，也阻礙了出租車駕駛員的收益。對于出租車運營管理不全面和不規范，導致存在司機拒載，違規拼車，故意繞路的情況，而乘客往往很難取證投訴，或者投訴之后沒有得到及時的反饋，導致整個出租車行業形象受損，惡性循環，使得出租車行業整體的發展受到阻礙[2]。

近年來很多國內外研究者針對以上問題均開展了一系列研究，2017年，肖露艷[3]提出了一種基于啟發式搜索的夜間公交路線生成算法進行夜間公交路線規劃。同年，由大連理工大學的張翔[4]收集到的出租車上下客GPS 數據進行預處理，篩選出超時顧客的出行數據。提出了DBSCAN-PAM 混合聚類算法，選擇地球球面距離作為聚類算法中的相似度，從而提升聚類的精度，使用基本遺傳算法規劃最優路線，目的使班車行駛距離最短。Lam 等人[5]提出了基于歷史數據的及時響應方法。在當前的交通信息和歷史數據沒有明顯變化時，按照之前的路線。Lin Jing Jie[6]提出了一種基于集合算子的模擬二元交叉的進化多目標拼車算法，此方法有效的減少了司機因拼客繞路帶來的資源利用不合理問題。以上算法雖然在一定程度上改進了出租車資源利用不合理的問題，但是算法相對復雜，本文結合目前出租車智能規劃算法優點的基礎上，引進時間差分算法，對比其他算法的優劣，設計構造出出租車智能規劃仿真模型，實現出租車的智能規劃，以一片特定區域為標本，通過爬蟲的方式獲取一定時間內的真實數據，驗證模型的可靠性和高效性，發展不足和模型補充，實現出租車、乘客、社會資源的高效利用和利益最大化。

1 時間差分方法的基本思想

在機器學習的眾多模型中[7]，馬爾可夫決策過程是重要的數學模型之一，通過在該過程使用動態規劃、隨機采樣等方法，其可以求解使回報最大化的智能體策略，并在自動控制、推薦系統等主題中得到應用。該過程主要由兩部分組成，其中一部分被稱為基于模型的動態規劃方法，在該方法下區分有策略迭代、值迭代、策略搜索等方法，其另一部分被稱作無模型的強化學習方法[8]，常見的有蒙特卡洛方法和時間差分方法（TD 方法）。作為一個被廣泛用于強化學習領域的方法，時間差分方法是強化學習理論中最重要的內容，時間差分方法的核心思想可以用文字寫作為：

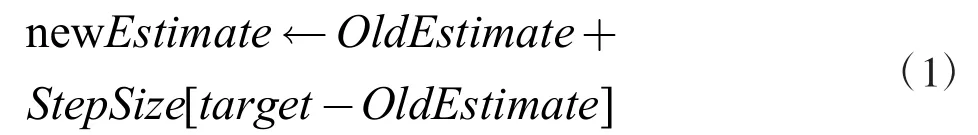
時間差分法是一個自展的算法[9]，意味著它可以運用估計的方法，針對前后兩個狀態值，可以用前一個狀態的估計值去預測另一個狀態的值。式中[target-OldEstimate]代表誤差，隨著智能個體不斷學習，能夠不斷縮小誤差值。StepSize 稱作學習率，范圍介于[0，1]，0 代表沒有學習，1 代表僅僅用了最近一步的信息，學習率會隨著時間增加而降低，直到飽和。

時間差分學習由蒙特卡洛算法演變而來[10]，稱之為contant-αMC，將其狀態更新值寫作：

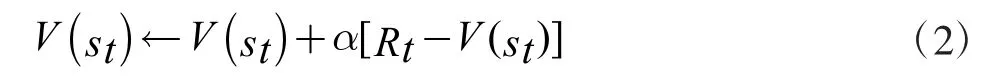
其中Rt 稱為實際積累的累計回報，α 是學習率，式子可以看作用累積回報作為狀態函數的估計值[11]，計算st 的實際積累回報Rt 和當前V（st）的偏差值，并用該偏差值乘學習率得到了V（st）的新估計值。為了解決蒙特卡洛算法中狀態值函數估計相互獨立[12]，需要經驗環境的弊端，將 Rt 換成得到了 TD（0）的狀態值函數過的更新公式：

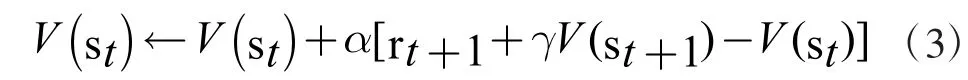
2 仿真實驗設計

2.1 實驗模型

本次實驗基于VISUAL STUDIO 平臺，嘗試在出租車智能規劃問題使用時間差分法來解決問題，結合時間差分法中的SARSA 和Q-learning 學習方法，得出和分析實驗結果。

為了使研究更加順利，我們將實際生活中的地圖抽取出規則的一部分，抽象成方格地圖用于研究，即將研究地圖的尺寸定義為長寬相等的一塊正方形區域，可以指定其地圖的尺寸分別是 5×5，10×10，20×20 等等。以長寬分別為十個單位為例，在地圖中以白色方格代表可行走路線，黑色方格代表障礙物即不允許行走路線。如圖1，我們選擇了10×10 共100 個格子組成的區域，將每一個方格從1 一直到100 進行編號，用文件將數據存儲。我們可以假定出發點，例如左上角的方格，設置成智能體開始行走的出發點，將右下角設置成終點，智能體出租車需要在避開障礙物，即黑色格子的前提下，尋找到達終點的最合適路線。并且在實驗的最后，能夠實現任意設置一個起點，一個終點，和一系列障礙點，都能夠讓智能體出租車找到一條移動距離最短的線路。

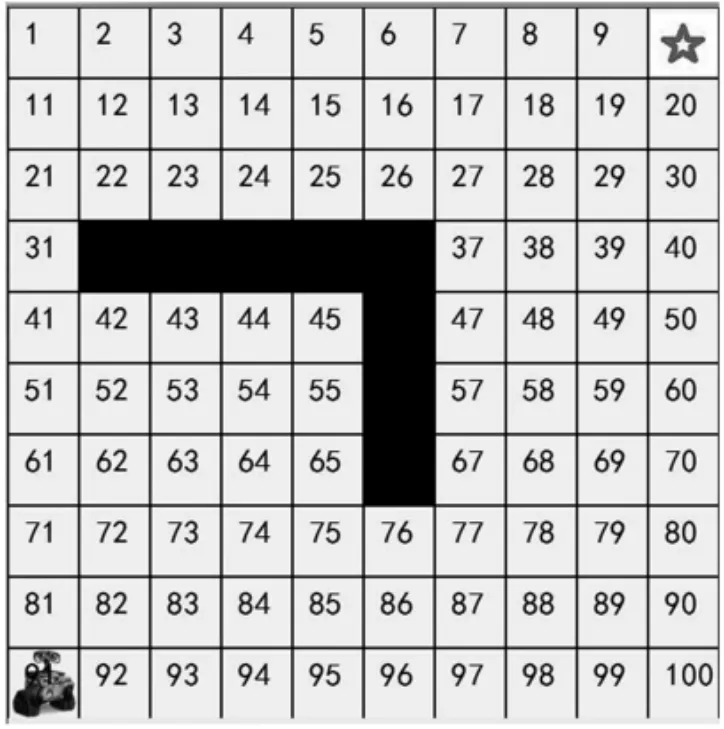
圖1 模擬實驗圖

2.2 實驗環境

作為馬爾科夫鏈的分支，時間差分法可以遵循馬爾科夫決策過程，針對該路徑規劃問題，將馬爾科夫四元組定義：

狀態：針對10×10 共一百個格子的區域，我們用1 到100 共一百個數將其表示，狀態1 定義為左上角格子對應的狀態，向下向右擴展，狀態100 定義為右下角格子的狀態，進行標號。同時使用二值的方法，將所有障礙點設置為-1，所有可通過的點設置為1，起始點定義為0，終點定義為2。當智能體運動過程中，一旦觸碰到障礙物，及賦值狀態為-1 的點，或智能體到達終點，即狀態賦值為2的點，則終止本次訓練，將智能體重新選擇初始位置，進行下一次循環訓練。

動作：規定在每一個方格中，智能體有且只有上下左右四個動作之一，從一個格子移動到相鄰的四個方格中間的一個，不能斜向沿著對角線移動，不能跨越一個格子向被跨越格子的相鄰及更遠的格子移動，每次移動都將被記錄，嘗試通過一個變量來表示和存儲這些動作。

獎勵：使用強化信號，對智能體的行為進行獎勵或者懲罰。若智能體到達右下角位置，給予1 的獎勵，當智能體到達障礙物所在的格子，會得-1 的獎勵，即懲罰。

轉移概率：假設成功按照預定進行轉移的概率為90%，即允許智能體收到動作指令后，有一定的概率偏差，不符合動作指令的預期，其有90%的概率能夠到達指定的位置，10%的概率不按照指令運動。

2.3 實驗參數

圖2 SARSA 方法

獎勵折扣因子：獎勵折扣因子決定智能體更看重眼前的立即回報，還是看重長遠的未來回報，取值介于0 和1 之間。當獎勵折扣因子越接近于0，說明智能體是“近視”，即智能體看重當前得到的立即回報；當獎勵折扣因子趨近于1，即智能體看重未來回報。在路徑規劃問題中，給予一定數量的訓練，智能體一般能夠找尋到最優路徑，即將實驗進行到終止狀態，因此將獎勵折扣因子設置成0.7，未來匯報和立即回報占據的比重接近。

學習速率：學習速率是一個取值0 和1 之間的實數。在參數設置過程中，如果學習速率的值太小，速度很慢，算法遲遲不收斂；若學習速率太大，算法反應過于劇烈，會導致算法收斂誤差較大獲得不正確的值。在本實驗中，將學習速率定義為0.01。

探索步數：探索步數是允許智能體移動次數的上限值，將探索步數設定在500，即允許智能體在一次訓練中做出500 個決策并對應運動，若在500 次之后仍然沒有到達終點，則說明這個策略是不夠優秀的，沒有必要繼續實驗，則選擇停止當前訓練，重新開始下一個訓練循環。

誤差閾值：由于時間差分法中使用的是一種迭代的思想，通過不斷迭代訓練可以將誤差盡可能縮小，為此設定一個終止條件，按照經驗將誤差閾值設定為1e-6。

當前算法中不需要進行輸入，只需要讓智能體運動，并且到達位置后給出相應的信號，在訓練的最后，以算法收斂或算法失敗作為一次訓練的終止。

3 仿真結果分析

在馬爾科夫決策過程的應用中，時間差分法具有重要應用，包括SARSA 和Q-learning 兩種方法，本設計中主要針對這兩種方法進行實驗。

針對路徑規劃，我們采用10×10 的格子作為實驗范圍，針對起點和終點，我們定義每次智能體向上移動，會有0.90 的概率向上移動，0.05 的概率向左移動，0.15 的概率向右移動；當智能體向右移動時，有0.90 的概率能夠向右移動，有0.05 的概率向上和向下移動，模擬了智能體在格子世界中獲得信號之后的行動判斷，模擬了不確定性。可以使用矩陣表示轉移概率：

圖3 Q-learning 方法

SARSA 算法是一種on-policy 的方法。設置好起始位置后，定義一個任意的初始動作，例如向左的動作，通過智能體與環境的交互，不斷更新算法策略，獲得獎懲。在規定的探索步數智能到達指定的重點位置，獲得函數的收斂和最優。

使用Q-learning 算法設置同樣的起始條件，它是一種off-policy 的方法，通過樣本和環境交互，與SARSA 通過下一步狀態決定下一步行動不同，Q-learning 的算法更為激進和冒險，通常直接選擇最優路線，同時也增大了智能體“失敗”觸碰到障礙物的危險。

由圖2 和圖3 中可以看出，針對該問題，SARSA 方法和Q-learning 方法從直觀上在大多數狀態都是最優，策略在每一個方格中采用的策略方法基本一致。針對每一次訓練中前后兩次策略的差值反映了每一次狀態和對應動作產生的錯誤偏差，針對兩種方法的收斂速度，在同一輪訓練中將誤差累加，就可以反映出收斂偏差，即所處的狀態和采取動作的改變情況。隨著訓練次數的變化，誤差越來越小趨近于零，當前輪次的訓練策略不再改變，能夠讓值函數收斂，停止訓練。當數值趨近于收斂之后，SARSA 的振幅會大于Q-learning，也符合Q-learning 更為激進的策略，即off-policy 的策略。

同時在實驗過程中，會出現SARSA 和Q-learning 獲得結果不同的策略，即相對次優策略。SARSA 采取的策略相對穩定，總是采取相對最優的策略，而Q-learning 根據當前策略產生的樣本決定當前動作，會導致比較冒險而造成不夠優秀的策略。隨著訓練次數的增加會逐漸固定路線，從而沿著當前路徑不斷優化，盡管可能探索和改變，還是能夠沿著原有的路線。

4 結束語

將時間差分方法引入出租車智能路徑規劃，智能出租車通過在模擬地圖中不斷與周圍環境交互來決定自己將會采取的行動，進而選擇當前步驟的最優策略，利用SARSA 和Q-learning 的方法，使智能體在模擬地圖中不斷尋找到路線，通過和環境進行交互來選擇當前狀態的動作，增加對環境的熟悉程度并且不斷更新路線策略。避免了傳統方法中收斂過早導致準確性不夠高的情況，實現得到最終的最優結果。通過模型仿真證明將時間差分法應用在基礎的路徑規劃中在模擬環境中是可行的，能夠合理避開障礙物和一些模擬的需要規避的禁行區域。