遷移與聯結：小學數學規定性知識的教學探析

李一婷

【摘 要】在小學數學教學中，規定性知識的教學存在著機械刻板、不夠深入的現象。本文以蘇教版數學一年級下冊“認識元角分”為例，通過分析教科書相關內容編排情況及學生學習情況，提出遷移關聯知識、突破認知瓶頸的具體對策：巧借“計數器”，理解新關系;利用整數豎式，創造新算法;聯系學生實際，調整學習內容。在規定性數學知識的教學中，教師不僅要善于轉變觀念，變“教”為“學”，更要做到瞻“前”顧“后”，促使有效遷移和聯結。

【關鍵詞】規定性知識 聯結 遷移

一、一次聽課引起的思考

筆者在一次教研活動中聽取了一節公開課——蘇教版數學一年級下冊“認識元、角、分”。在教學元、角、分的關系時，一個教學小片段引發了筆者的深思。其教學實錄如下：

師：同學們，一本練習本1元，我付10角可以嗎？

生：可以，10角就是1元。

師：對了，我們一起來數一數：1角、2角、3角、4角……9角、10角。10角就是1元，1元等于10角。那你們知道1角等于幾分嗎？

生：我知道，1角等于10分。

師：你是怎么知道的呢？

生：我媽媽告訴我的，1角就是10分。

師：真棒！那我們再來數一數：1分、2分、3分、4分……9分、10分。1角等于10分。這就是元、角、分之間的關系。

翻閱義務教育教科書，筆者發現教材編排與上述教學過程相同：①通過購物情境告知學生“10角就是1元”;②通過數數感受“1元=10角”“1角=10分”。一切看上去暢通無阻、水到渠成，但似乎又有些說不清楚、道不明白的遺憾。從知識類型角度來說，元、角、分之間的關系是數學中的一種規定性知識，對于規定性知識的教學，教師往往無從下手，似乎只要簡單告知學生就能完成教學，那學生對這些知識到底掌握得如何呢？課后，筆者對這個班的學生做了一個測試和訪談（見圖1）。

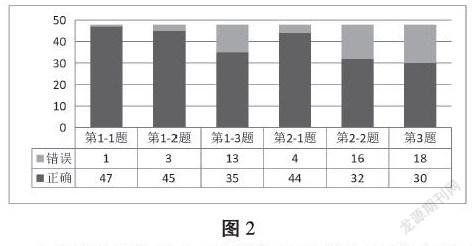
測試完成后情況統計如圖2。第1-1題、第1-2題和第2-1題學生完成情況較好，正確率均達到了90%以上，而第1-3題、第2-2題及第3題完成情況一般，正確率分別為72.9%、66.7%和62.5%。正確率較低的這三題均涉及了元角分之間的間接轉換，而不是像“2元=（ ）角”這樣的直接轉換。在訪談中，學生對于“怎么知道‘1元=10角’”這個問題的回答均為“老師教的”“家長說的”“看書的”三種情況中的一種，至于“為什么‘1元=10角’”則鮮有學生能回答。從測試和訪談的結果來看，通過上述教學，學生對于元、角、分關系的認識浮于表面，因此也只能完成較為簡單的、低水平的習題，并未真正理解三者之間的關系，故而對于稍復雜的、中高水平的習題完成效果較差。

在小學數學教學中，像這樣“人為規定”“約定俗成”的知識并不少見，在教學時也無不存在著機械刻板、不夠深入的現象，學生往往掌握效果極其一般。如何讓學生理解規定背后的原因，體會規定的合理性和必然性，讓“規定性的知識”的學習變得有意義、有意思呢？這都是值得我們深入思考和躬身實踐，尋求解決辦法的問題。

二、遷移關聯知識，突破“元、角、分”認知瓶頸

德國數學家康托說過：“數學的本質在于它的自由。”任何數學規定性知識在其“被規定”“被濃縮”之前，并不是無中生有的，也不是枯燥乏味的，而是有著其背后深刻的“故事”和“原理”。那么，元、角、分關系背后的“原理”又是什么呢？如何讓學生深刻理解它們三者之間的關系呢？筆者做了以下一些思考和嘗試。

（一）巧借“計數器”，理解新關系

“認識元、角、分”是一年級下冊第五單元的內容，此前，學生已經通過計數器認識了“個位”“十位”和“百位”，感知了“10個一是1個十”和“10個十是一百”。整數的三個數位與人民幣的三種單位似乎可以對應，而“滿十進一”的規則也同樣適用于元、角、分之間的換算。因此，筆者靈機一動，能不能借助計數器來認識新的關系呢？

師：同學們，為了便于計算，我們規定了元、角、分之間的關系與百位、十位和個位之間的關系類似。我們可以在計數器上來撥一撥、數一數。

（出示貼好“元”“角”“分”的計數器）

師：老師撥，大家一起來數。1角、2角……

生：1角、2角、3角……9角、10角（1元）。

師：對，10個1角就是1元，所以我們說，1元=10角。

師：那你們知道1角等于多少分嗎？

生：可以在計數器上撥一撥、數一數。

師：那你來撥一撥，我們一起數一數。

生：1分、2分、3分……9分、10分（1角）。

師：那你知道了什么？

生：10個1分是1角，所以1角=10分。

師：看來，計數器的作用真大，不僅可以幫助我們數數，還可以幫助我們數“錢”。（學生開心地笑了起來）那從這個“計錢器”上，你還能知道些什么知識呢？

生：我想到了“元”和“分”之間的關系。因為“10個十是一百”，那“10個1角是1元”“10個1角就是100個1分”，所以“1元等于100個1分”。

師：哇，你真是個會思考、會推理的孩子。掌聲送給你！

在這個過程中，改編原有的學具——“計數器”，制作新學具——“計錢器”，讓學生在熟悉的數數的情境中遷移已有的知識，從而內化新知識，達到了輕松而高效的學習效果。荷蘭數學教育家弗賴登塔爾認為：數學教育方法的核心是學生的“再創造”。作為教師，我們不必將各種固定性的知識灌輸給學生，這樣的學習對學生來說是不加判斷的機械記憶，是一種零散的淺層學習。教師應該創造合適的條件，引發學生的深度學習，讓學生充分聯系自己的已有知識經驗，主動地理解、聯系、遷移和建構知識，這樣，統一的規則、法則和定律在課堂中自然就會呼之欲出，學生自然也掌握得更牢固，記憶也更深刻。

（二）利用整數豎式，創造新算法

通過初步嘗試，筆者感受到了利用計數器來認識人民幣的相關知識對學生大有益處。那么整數計算的方法是否同樣可以適用于人民幣的計算呢？筆者開始了第二次嘗試。

通常情況下，學生在計算諸如“5角和8角合起來一共是多少錢”的問題時，普遍采用三種方法——①學具操作：先擺出5張1角，再擺出8張1角，數一數一共有多少個1角，再說一說是幾元幾角。②先計算后換算：5角+8角=13角，10角=1元，1元+3角=1元3角。③分與合推想：把8角分成5角和3角，先算5角+5角=10角，10角=1元，再算1元+3角=1元3角。這三種方法思路雖然都比較清晰，但都有各自的弊端：方法①需要借助學具擺一擺，再想一想、算一算，這種側重依賴于具體形象的方法往往過于煩瑣，不夠簡便;方法②與方法③則需要學生經過三步思考才能逐步推導出答案，完全脫離了具體的實物，這種方法對于一年級的學生來說過于抽象，學生難以在頭腦中直接有條理地進行思考和計算。

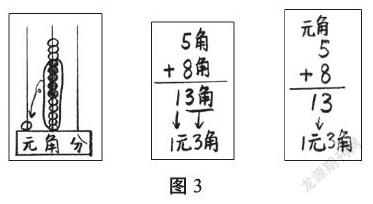
在教學中，筆者鼓勵學生繼續借助計數器，并嘗試列豎式進行計算，學生積極思考，想出了多種方法（如圖3）：

而后，又利用“元、角、分豎式”計算了“2元-1元8角”（如圖4），學生紛紛表示：用豎式來計算人民幣的加減法太方便了！

小學生思維發展經歷著從具體形象思維為主向抽象邏輯思維過渡的階段，純粹的具體形象（擺學具）或純粹的抽象（推理）都不利于學生的數學學習。因此，我們要遷移整數豎式計算的方法，架起具體與抽象之間的橋梁，幫助學生掌握數學知識，發展思維能力。縱觀小學階段的數學學習，像這樣利用計數器或豎式進行計算的方法同樣適用于“每相鄰兩個單位之間的進率是10”的長度單位“米”“分米”“厘米”“毫米”之間的換算和計算。

（三）聯系學生實際，調整學習內容

蘇教版數學一年級下冊第五單元“元、角、分”的學習內容一共安排了3個課時，分別是“認識1元及1元以下的人民幣”“認識大于1元的人民幣”，以及“練習十”。但在實際教學中，3個課時是遠遠不夠的，并且學習的內容跨度較大，因此應根據學生的實際情況，適當地進行調整。

可以調整章節學習內容的順序。如，在教學第五單元“元、角、分”時，練習中經常會出現超過20的退位減法及兩位數加兩位數的進位加法，而這部分學習內容被安排在第六單元，顯得有些滯后。因此，在教學中，教師可以根據自己的教學情況，合理調整單元教學內容的順序，這樣更有助于學生學習計算人民幣。

可以適當增加變式練習內容。在蘇教版教學教材中，“元、角、分”這一單元的練習十第一題直接出示了元、角、分的換算，但在前面的兩節新授課中并未對人民幣的換算和計算加以強化，由此導致大部分學生不會換算和計算。人教版的一年級教材編排了“簡單的計算”這一課時，將人民幣的單位換算和加減法計算作為例題進行教學，進而拓展到解決實際問題，這樣有梯度的習題安排有助于學生深入掌握。因此，在教學時，我們可以適當增加課時和練習內容。

三、遷移與聯結：數學深度學習的關鍵

在小學數學的學習內容中，有大量的規定性知識，主要是一些數學概念、名稱、術語、表示方法等，這一類知識往往比較抽象，學生不易理解和掌握。在教學中，我們要努力做到以下幾點：

（一）轉變觀念，變“教”為“學”

史寧中教授說：“數學素養的培養，特別是創新人才的培養，是‘悟’出來的而不是‘教’出來的。”在教學中，我們要關注規定性知識的教學，轉變教學的方式方法，根據學生已有的知識經驗，設計或提供可探索的情境，讓學生在探索的過程中遷移、運用所學知識，“悟”出解決問題的方法，從而更好地理解數學，實現深度學習。

（二）瞻“前”顧“后”，促使有效遷移和聯結

作為一名小學數學教師，要熟悉學生的已有知識經驗，更要十分熟悉學生將要學習的知識，要掌握整個小學階段的數學內容及其體系，要了解規定性知識的“來龍去脈”，進一步展現“濃縮”背后的精華，這樣才能全面而準確地對規定性知識展開教學。

一次小小的嘗試，僅僅只是規定性知識教學探索的一個開端，規定性知識創新教學方法的研究任重而道遠。了解規定性知識的主觀特征和產生背景，理解規定背后存在的合理性，帶領學生經歷知識產生的過程，才能形成規定性知識有效學習的路徑。