造境·串問·靈動:從中考題談情境教學*
——以“直尺作圖”為演示案例

江蘇省鎮江市宜城中學(212028) 張 潔

1 問題的提出

省視當下,尺規作圖復習題與中考題都會考查經典的尺規作圖問題,結合復習課,目前面臨著以下問題: 尺規作圖基本概念掌握不牢固、數學復習課堂單向傳輸、尺規作圖到直尺作圖創新轉化困難. 這些問題使尺規作圖復習課堂效率不高,有必要在教學方式上進行創新,下文擬從“情境”與“問題串”的視角作一些探討.

2 情境教學課堂演示案例

2.1 示例1

(2019年浙江· 嘉興卷· 改編) 在6×6 的方格紙中, 點A、B、C都在格點上,按要求畫圖:

問題1: 在圖1 中找一個格點D,使以點A、B、C、D為頂點的四邊形是平行四邊形.

圖1

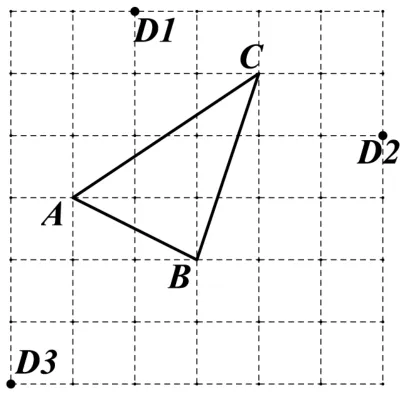
圖2

師: 我們學習過尺規作圖和網格作圖,你能找到對應的點嗎,你是如何找到呢?

生: 如圖2,根據平行四邊形的性質,對邊平行且相等,數格子可以找到對應的D1,D2,D3.

問題2: 在圖3 中僅用無刻度的直尺,把線段AB三等分(保留畫圖痕跡,不寫畫法).

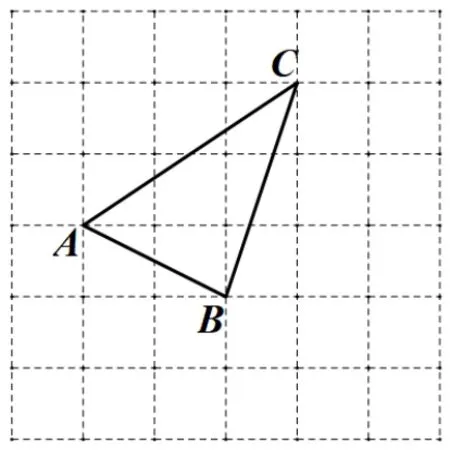
圖3

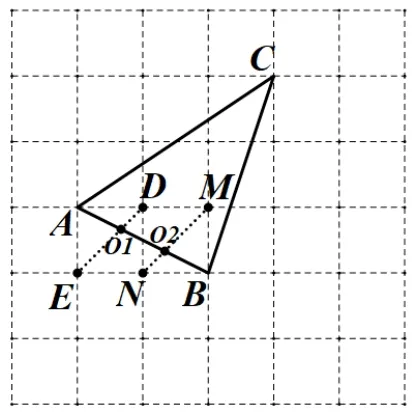
圖4

師: 根據我們復習的尺規作圖、直尺作圖的內容,你會畫什么平分線呢?

生: 垂直平分線.

師: 雖然沒有復習過三等分點的畫法,你能借助直尺與網格以及圖形的性質找出三等分點嗎?

生: 可以,如圖4,我們可以找到格點D、E、M、N,連接DE、MN,與AB交于O1,O2,所以AO1:AO2= 1 : 2,同理得出O1,O2是三等分點.

問題3: (改編題) 在圖5 中僅用無刻度的直尺, 畫出∠APD的角平分線(保留畫圖痕跡,不寫畫法).

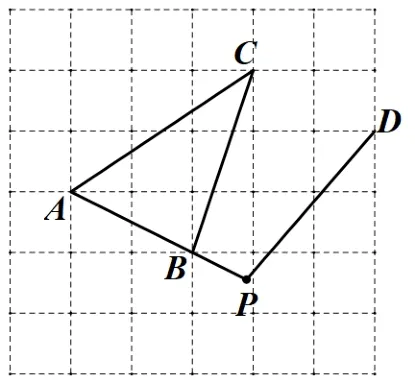
圖5

圖6

師: 三等分點我們運用了相似三角形的知識,而圖5 出現了非格點,你會利用什么工具解決呢?

生: 直尺和圓規.

師: 但是問題3 給出的限定條件是: 僅用無刻度的直尺.你有解決辦法嗎?

生: 我們探討發現,D是問題1 中的D2點,我們可以利用問題1 中的平行四邊形的性質,連接CD、AD、BD,AD與BC交于O,再根據等腰三角形的性質,連接PO并延長,即PO為角平分線.

評析: 在蘇科版八年級上冊課本中,提到垂直平分線的尺規作圖. 本題三等分點難度較大,借助九年級已學相似三角形的有關知識,從垂直平分線引出三等分點的問題串. 由問題改編加入問題3,因為在直尺作圖的情境問題串的條件下,無法用圓規作圖,只能利用直尺,所以本題又回到八年級等腰三角形的基本性質的知識點上,問題迎刃而解. 問題3的加入,可以讓學生充分利用問題1 與2 的結論思考并解決問題,從“造境”到“串問”,環環相扣,讓學生變得靈動.

2.2 示例2

(2019年天津卷· 改編) 邊長為1 的正方形網格中, ΔABC的定點A是格點,B是中點, ∠ABC= 50°,∠BAC=30°,經過A、B兩點的圓,圓心在AC上.

問題1:AB=____;

師: 如圖7,如何利用網格計算線段長度?

生: 根據勾股定理知:AB=

問題2: (改編題)用無刻度的直尺,找出圓心O;

師: 在復習過示例1 的前提下,你會利用直尺作圖嗎? 你能說出理由嗎?

生: 如圖8,找到格點E、F,連接EF,與AC的交點即為圓心O.

問題3: 請你在給定的網格中, 用無刻度的直尺, 在ΔABC的內部畫P,使其滿足∠PAC= ∠PBC= ∠PCB,并簡要說明P的位置是如何找到的(不要求證明)_______.

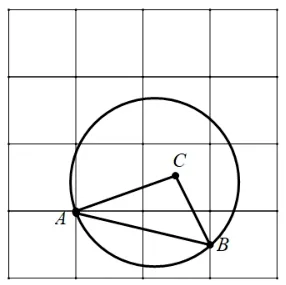
圖7

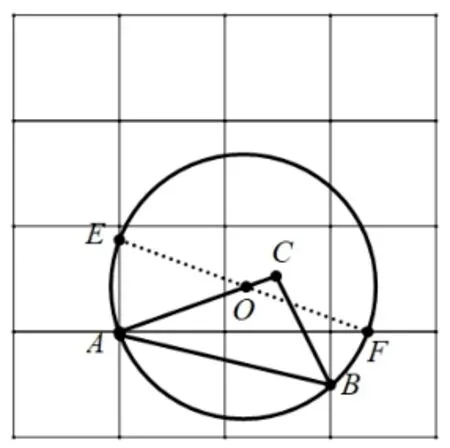
圖8

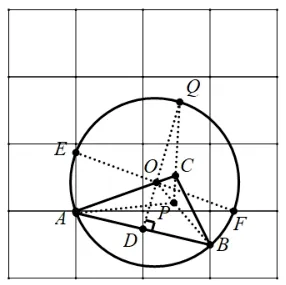
圖9

師: 畫角相等你會用什么方法呢?

生: 尺規作圖畫一個角等于已知角.

師: 問題3 的限定條件仍然是直尺作圖,你是用什么基本知識解決的呢?

生: 如圖9, 設AB與格子交于D點, 連接DO并延長交于Q, 因為D是AB的中點, 所以OD⊥AB,易 知ΔQOC∽= ΔBOC, 所 以QC=BC, ∠QCO=∠OCB= 100°, 所以得∠PCB= ∠PBC= 20°, 由此得ΔAOP∽= ΔQOP,即∠PAC=∠PCB=∠PBC=20°.

評析: 本題難點在于問題,大部分學生不明所以. 本題根據圓的有關性質,改編加入問題2,造境、串問并讓學生感到題目不再陌生. 結合三角形全等的性質得出推導過程,重現本題的重難點,讓學生讀透問題串,掌握問題三角形全等與圓有關性質的本質,讓課堂變得如此靈動.

2.3 基礎知識的回歸——追根溯源

仔細閱讀上述3 道中考題及改編題,可以看出,題目中的情境問題串已經指向課本中的三角形、平行四邊形、圓的相關知識點,但學生在復習過程中很難看透問題中的知識點.此時,需要教師引導學生復習書本知識,系統整理課本關聯知識,找到其知識本源,回歸課本知識,以不變應萬變.

3 尺規作圖情境教學探討

3.1 引導——從單一到系統

由已學知識轉化為對未知問題的解決,需要對知識的整理、消化. 中考復習課,教師可以根據中考真題加入情境以及問題串, 作好知識鋪墊, 引導學生不斷探討, 提高學習興趣.以上文中“直尺作圖”為例, 由2 道中考題引申到n個知識點,舉一反三. 九年級學生學習習慣已經養成,可以在教師的引導下, 改變過去單純由教師講解知識點的傳統教學模式,通過題串讓學生動起來,把自主權交給學生.

3.2 設問——從單向到互動

九年級學生在掌握了3年的數學知識的基礎上,復習時間較長,難度較大,部分學生對數學感到厭倦. 新題型的情境問題串引入,可以提高學生的學習興趣和學習能力,也使教學不再枯燥無趣. 上文的中考題都是以情境問題串為核心內容,以“直尺作圖”作為切入點,以情境問題作為探討的線索,循序漸進地貫徹到中考題的每一個問題中. 改編題型以課本的知識為情境,圍繞三角形、平行四邊形、圓的有關性質進行情境層層設問,自然過渡到已經復習的知識點. 為此,教師在復習過程中,需要肯定學生的創造性,引導其透過表象看本質,提高復習效率,促進核心素養提升.

3.3 引申——從舊知到新知

從2019年尺規作圖的題型可以看出,“直尺作圖”并不是書本上提到的內容,學生遇到新題型感到束手無策,其主要原因在于對書本知識掌握不夠牢固. 嘉興題則是從平行四邊形入手,問題串“直尺作圖”的切入點則是相似三角形的基本性質、等腰三角形的三線合一基本性質;天津題則是從圓的相關知識作為切入點,問題串的解決是結合三角形全等的基本判定定理. 這些知識是我們中考復習中書本的基礎知識,也是復習重點. 直尺作圖雖然是新題型,但是教師復習時加入題串可以讓學生自然地過渡到新知.

4 結語

中考復習中,教師要根據新課標的要求,引導學生從中考題看基礎知識,也就是說,要促使學生在原有的數學活動經驗基礎上,思考數學知識的發生、發展過程. 中考復習時間緊、任務重,要在有限的時間內提高復習效率,就要系統地復習書本基礎知識,回歸課本. 教師在中考復習中根據真題設置情境問題串,引導學生牢固掌握舊知,并結合情境的引導,讓學生不斷從舊知引申出新知,理解、掌握新知,有效提高考試成績.