六何引導數學教學 先行組織培養思維*
——以“對數函數及其性質”教學設計為例

廣西師范大學數學與統計學院(541006) 林素安 劉存華 周 瑩

1 問題提出

《普通高中數學課程標準(2017年版)》明確指出“在數學課堂中要培養學生的邏輯推理能力,將學生思維能力的培養貫徹于整個教學過程中”[1]. 可見高中數學是關注“過程”的教學,注重學生思維能力的培養,傳統課堂提問的問題層次太低,過于注重知識的記憶,缺少思維性[2]. 許多一線教師在教授新授課時往往會忽略學生的最近發展區,在課堂中的提問超出了學生的能力范圍,體現不出學生思考的過程,導致學生學習新授課時思路不清晰,難以理解新知的本質. 因此,如何在新授課中使學生明晰知識的本質,由淺入深的培養學生的思維能力是一個亟待解決的問題. 本文嘗試在新授課中以“六何”認知鏈指導先行組織者的應用,構建以先行組織者為載體,培養學生思維能力為主線的課堂教學模式,并給出教學設計過程,以期為幫助學生明晰新知的本質、培養思維能力提供新的方法路徑.

2 “六何”認知鏈與先行組織者的整合

2.1 “六何”認知鏈理論

“六何”認知鏈是周瑩教授基于如何在新授課中培養學生思維提出的一種教學過程理論.“六何”認知鏈以問題情境出發,從問題意識的角度進行教學設計,展現了知識的來龍去脈,具有問題性、可操作性、層序性以及完整性,具體內容如下[3]:

“從何”: 新知從哪里而來;“是何”: 新知的本質屬性和特征是什么;“與何”: 新知與舊知有何區別及聯系;“如何”: 所學新知如何學以致用;“變何”: 對新知或問題的條件、結論、方法進行螺旋上升的變式;“有何”: 總結歸納本節課在知識、情感、方法上有何收獲[3].

2.2 先行組織者理論

先行組織者由美國的奧蘇貝爾于上個世紀60年代提出.“先行組織者”指先于數學知識前,呈現給學習者的一種引導性材料,可幫助學習者建立新舊知識間的聯系,進而加強新知識的學習[4].“先行”二字指知識建構過程的先行,引導材料可在學習過程中的任意階段呈現. 因此,先行組織者的功能是為新知識提供觀念上的固著點,通過對學習者原有的知識結構進行加強,從而達到促進學習者的有意義學習和記憶保持的目的. 根據學習者對新知識學習的熟悉程度,先行組織者可分為陳述型組織者和比較型組織者;根據組織者和新的學習內容之間的包容層次和抽象程度可分為上位組織者、下位組織者和并列組織者[5].

2.3 “六何”認知鏈與先行組織者整合的教學模式

“六何”認知鏈做為一種理論指導需要應用于具體的教學實踐中,而先行組織者作為一種應用型材料則需要系統的理論指導. 將先行組織者進行分類后的“陳述型組織者、比較型組織者、下位組織者、并列組織者”與“六何”認知鏈有著互通點,都注重知識的來龍去脈、構建認知過程的手腳架. 因此,將“六何”認知鏈與先行組織者進行有機的整合,并凝結于教學設計當中,可幫助學生搭建認知的手腳架,做好知識間的過渡,明晰新知的本質,逐步培養學生的思維能力[6]. 將分類后的先行組織者與“六何”認知鏈整合成教學模型(如圖1),并依此進行新授課的教學設計.

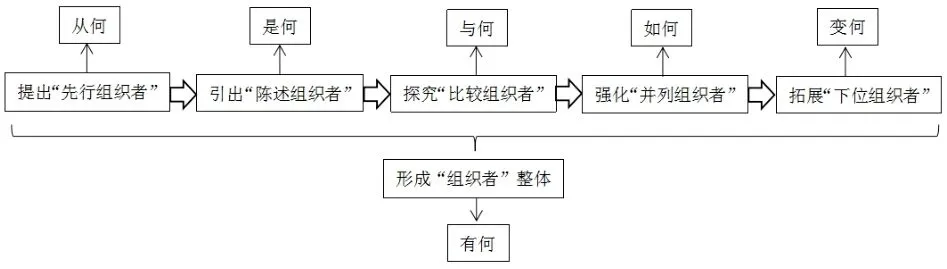
圖1 教學模型

3 先行組織者在“六何認知”指導下的教學設計

先行組織者是為開啟學生思維提供的教學材料,在課堂上得到很好的實施需要一定的理論指導. 本文在中國知網近幾年與“對數函數”相關文獻的研究基礎上,嘗試運用上述教學模型整合、優化“對數函數及其性質”一節內容,并將教學過程設計如下:

3.1 課例背景

“對數函數及其性質”選自《高中數學人教A 版》(必修一)2.2.2 節,繼指數函數的圖形與性質的學習之后,是對函數圖像的深入認識,也是研究基本初等函數圖像及性質的基礎,在本章中具有銜接的作用. 本節課的主要內容是通過對比指數函數性質的探究學習方式,進而探究得出對數函數的圖像及性質,并將其運用于解決實際問題中. 學生在本節課的學習之前已具有一定的探究函數圖像能力. 以“六何”認知鏈指導先行組織者在各教學環節中的運用,培養學生的思維能力.

3.2 教學過程

(1)追溯從何,引入新知

基于“對數函數從哪里來? ”的思考,通過引入生活中的例子創設問題情境,提出“先行組織者”,在觀察具體函數例子的過程中,得出對數函數的定義.

問題1考古學家一般通過提取附著在出土文物、古遺址上死亡生物體的殘留物,利用估算出土文物或古遺址的年代. 根據問題的實際意義可知,對于每一個碳14 含量p,通過對應關系都有唯一確定的年代t與它對應,那么t和p有什么函數關系?

問題2大西洋鮭魚每年都要逆流而上, 游回產地產卵. 研究鮭魚的科學家發現鮭魚的游速可以表示為函數單位是m/s,其中o表示魚的耗氧的單位數,那么v和o有什么函數關系?

設計意圖巴金說:“方向比努力更重要”. 故以“從何”為教學的起點,對“對數函數從何而來”進行思考,創設生活中的“問題情境”這個先行組織者,使學生找準本節課的學習目標,激發學生濃厚的學習熱情,從觀察具體函數中完成對對數函數的首次感知,形成對數函數模型,為探究對數函數的性質做鋪墊.

(2)探究是何,把握本質

基于“對數函數的性質有哪些? ”的思考,在學生探究的過程中引出“陳述組織者”,把握對數函數性質的本質.

問題3在數學中如何定義上述問題中形如y= logax的函數? 其值域和定義域的取值范圍是什么?

問題4為什么在對數函數解析式y= logax中,a ＞0,且a ?=0,x ＞0?

問題5如何利用函數的性質研究y= log2x和的圖像? 繪制并觀察這兩個函數圖像, 可以得到哪些結論?

設計意圖“是何”目的是明晰知識點,把握所學知識的本質屬性. 從學生的最近發展區出發,使用問題導向法提出問題3、4,使學生明晰對數函數的本質屬性,理解每個字母及取值范圍的含義. 再基于學生已有的探究能力,引導學生繪制出兩個最基本的對數函數圖像. 在學生對比觀察的過程中引出“陳述組織者”,把握對數函數圖像的本質內容,完成對對數函數的二次感知,從中滲透數形結合的數學思想,培養學生的思維能力.

(3)關聯與何,拓展概念

基于“對數函數的性質與哪些知識有關? ”的思考,引導學生對比探究“比較組織者”,設計如下問題:

問題6回憶上節課所學習的內容,有哪些知識點與對數函數有聯系?

問題7用類似探究指數函數的方法,小組內進行合作探究,選取底數a的若干個不同的值,觀察不同底數的對數函數在同一直角坐標系內的圖像,你們有什么發現?

問題8能不能把你們的發現整理成表格?

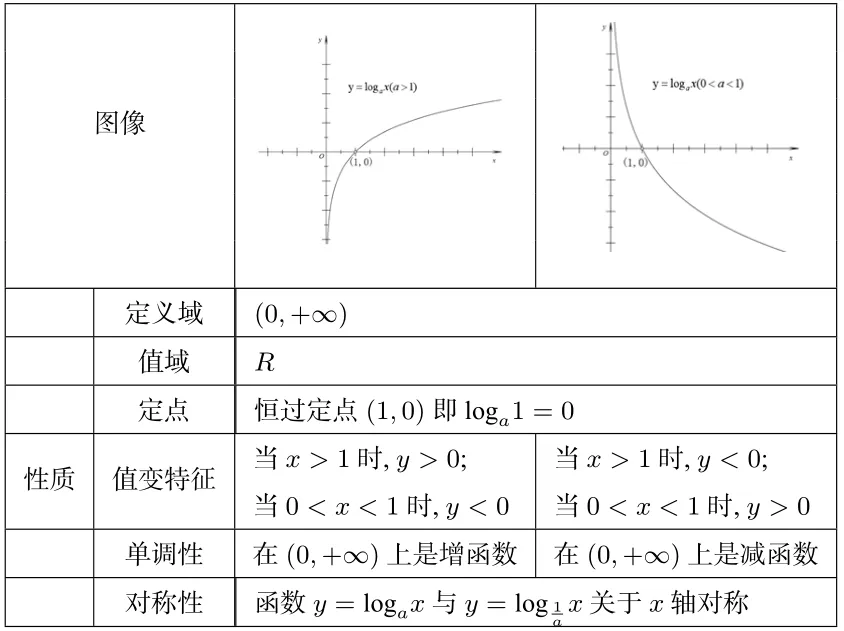
表2:對數函數的性質

設計意圖“與何”目的在于聯系相關知識,完善知識體系. 教師再次充分利用學生的最近發展區,在學生的能力范圍內引導學生進行小組合作,探究“比較組織者”. 通過比較底數在0＜a ＜1、a ＞1 范圍內不同對數函數的圖像,將抽象的對數函數直觀化,體會不同底數對對數函數性質的影響,從而培養學生的直觀感知能力及數形結合思想,完成對對數函數的第三次感知,拓展對數函數的概念. 在問題8 整理歸納中,使學生形成系統的知識框架(如表2),為“如何”打下堅實的知識基礎.

(4)操作如何,學以致用

學生探究出對數函數的性質后,掌握的效果如何? 對學生進行當堂檢測:

問題9求下列函數的定義域

(1)y=logax2;(2)y=loga(4-x)

問題10比較下列各組中兩個值的大小

(1)y=log23.4,y=log28.5

(2)y=log0.31.8,y=log0.32.7

(3)y=loga5.1,y=loga5.9(a ＞0,且a ?=1)

(4)如圖3 所示,有四個對數函數

①y=logax, ②y=logbx, ③y=logcx, ④y=logdx

試比較a,b,c,d的大小

圖3

設計意圖“如何”是本節課的關鍵點. 教師通過強化“并列組織者”,對學生提出了兩道簡單的求定義域問題和比較大小問題. 目的在于考查學生是否掌握了對數函數的定義域為x ＞0,以及如何應用圖像比較對數值的大小. 在學生的實際操作過程中,體會如何應用對數函數的性質解決簡單的問題,再次深化學生數形結合的思想,培養學生的思維,加深對對數函數的理解,完成對對數函數的第四次感知.

(5)拓展變何,深化概念

基于“拓展對數函數的性質”,引導學生拓展“下位組織者”,設計如下問題:

問題11在指數函數y= logax中,x為自變量,y為因變量. 如果把y當成自變量,x當成因變量,那么x是y的函數嗎?

問題12運用對指互化公式,繪制y= log2x與y= 2x的圖像,你們有什么新的發現?

問題13通過觀察可以發現這兩個函數關于y=x對稱,如何給這樣的函數下定義? 還可以繪制出其他類似的函數嗎?

設計意圖“變何”是本節課的高潮部分.“變式拓展”可以幫助學生多角度地理解知識本質,生長出對對數函數性質新的認識. 教師通過拓展“下位組織者”,學生可發現對數函數的新性質: 與同底的指數函數互為反函數. 通過問題13 讓學生自己給函數下定義,體驗數學的嚴謹性,深化對數函數的性質,發散數學思維,完成對對數函數的第五次感知.

(6)反思有何,構建體系

基于“學習本節課后有什么收獲”,師生共同進行小結:

問題14今天的課堂即將接近尾聲,讓我們共同梳理本節課學習的流程有哪些?

問題15有哪位同學可以將今天的收獲用思維導圖呈現出來嗎? (師生共同完成)

設計意圖“有何”在一堂課中起到了畫龍點睛的作用.先通過梳理本節課的學習思路,加深學生對所學內容的印象.再通過充分運用先行組織者策略關聯相關知識,師生用思維導圖共同繪制本節課的框架體系(如圖4),將所學知識納入已有認知體系,形成“組織者”整體,完善學生的知識結構,培養學生的系統思維[7].

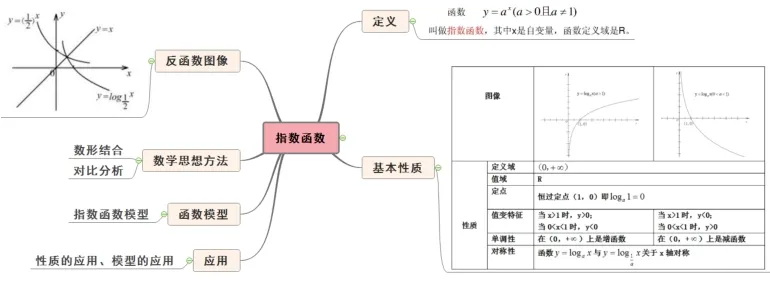
圖4 指數函數思維導圖

4 教學反思

4.1 在教學目標的設計上,選擇組織者

一堂好課離不開教師精心的設計. 要在一堂課中由淺入深的培養學生的思維,教師在教學目標的確定時就要充分考慮學生的最近發展區,利用學生已有的知識經驗來設計教學過程. 在哪個教學過程中應用哪個組織者來引導學生進行學習? 怎樣通過組織者來培養學生的思維? 都要在教學設計中有所體現,體現出先行組織者的可操作性. 將“六何”認知鏈與先行組織者進行整合,形成教學模型,使得每個教學過程都有理論指導,幫助教師梳理教學思路,選擇合適的組織者進行教學.

4.2 在六何認知的指導中,應用組織者

依據學生的最近發展區,開展教學活動,應用先行組織者: 在“從何”中提出“先行組織者”;在“是何”中引出“陳述組織者”;在“與何”中探究“比較組織者”;在“如何”中強化“并列組織者”;在“變何”中拓展“下位組織者”;在“有何”中形成“組織者”整體. 以指數函數的教學為例,在課堂導入環節以具體的例子呈現“先行組織者”,降低學生的理解難度,并在接下來的學習中依次應用不同的組織者,發揮各自不同的優勢,逐步培養學生的思維.

4.3 在教學問題的設計下,培養思維力

在“六何”認知指導下的問題設計由淺入深,逐步帶領學生由潛意識的思維進入到深層次的思維,調動學生學習的積極性,并給予學生學習的成就感. 如在“與何”環節的合作探究,由三個由淺入深的引導性問題,引領學生進入數學探究的世界,在探究中發現成就并培養思維. 學生思維的培養不僅體現在一節課中,還需要在整個教學中不斷的滲透. 教師對學生思維的培養任重而道遠,需要教師不斷地進行教學反思,嘗試將該教學模型應用于其他類型課程,嘗試新的教學方法,探究出一條發展學生系統思維的道路.