Bootstrap法與H-L法中位數差值區間檢驗在非劣效試驗中的模擬比較研究*

成都醫學院公共衛生學院(610500) 毛 昂 曾子倩 魏 敏 陳曉芳 陳衛中

【提 要】 目的 比較Bootstrap法和Hodges-Lehmann法(H-L法)在中位數差值非劣效性檢驗中的特點，為相關研究中統計學方法的選擇提供依據。方法 以某臨床試驗中試驗組與對照組咽痛消失時間的比較為基礎，通過計算機模擬生成單組樣本量分別為20、30、50、100、200各500個兩獨立樣本，分別服從參數為90h(試驗組)、100 h(對照組)的Poisson分布。針對每個樣本采用基于正態近似和百分位數的Bootstrap法、H-L法求得中位數差值的置信區間，并通過置信區間下限與非劣性界值進行比較，得出三種方法的檢驗效能。結果 三種方法均隨著樣本量增加，檢驗效能增加。在樣本量為20時，H-L法與正態近似法檢驗效能相當(25% vs.24%)，且都高于百分位數法(19%)。在樣本量為30、50、100時，H-L法檢驗效能高于正態近似法與百分位數法，且正態近似法高于百分位數法。在樣本量為200時，三種方法的檢驗效能相當，均在95%以上。結論 整體來看，H-L法獲得的區間最窄且最穩定，檢驗效能最高，尤其在樣本量不大時建議選擇H-L法。

非劣效性試驗(non-inferiority trials)被廣泛應用于藥物臨床試驗研究。有關非劣效性檢驗的方法主要有假設檢驗法和區間檢驗法兩種[1]。目前針對定量資料均數非劣效性檢驗的方法較為成熟，如t檢驗法、均數差的置信區間法，以及基于模型邊緣均數置信區間法等[5]。但越來越多的臨床試驗中以某一臨床事件發生或達到預先規定標準的時間分布情況作為藥物的療效指標[2]，其觀察結果多呈偏態分布，且存在不確切值為開口資料，采用中位時間作為療效描述和比較指標更為恰當[3-4]。針對中位數的非劣效性區間檢驗的主要有H-L法和Bootstrap法兩種，關于兩種方法在非劣效試驗中的檢驗效能比較報道較少。因此，本文以評價某醫藥公司生產的七味清咽氣霧劑咽痛緩解時間為例，比較上述兩種區間檢驗方法在不同樣本量下的檢驗效能，為相關研究中統計學方法的選擇提供依據。

對象與方法

1.對象

為評價某公司生產的七味清咽氣霧劑的有效性，以標準藥物作為對照，共納入280名受試對象，隨機等分為試驗組和對照組。以疼痛消失時間為有效性評價指標，在6天的臨床用藥觀察中，對于咽痛未消失患者的疼痛消失時間記為“>144h”，為典型的開口資料。試驗結果顯示對照組的咽痛消失時間的中位數為90h，試驗藥物組疼痛消失時間中位數為100h，非劣效性臨界值Δ設定為15h，即中位數差值>-15可做出試驗藥物非劣于標準藥物的結論。

2.方法

(1)數據分布及參數的選擇

本研究中，假定數據服從Poisson分布，即試驗組和對照組的結局變量X1、X2分別服從參數為1和2的Poisson分布，結合試驗結果記為X1～P(90)，X2～P(100)。

(2)樣本量的確定

根據經驗，結合臨床實際，模擬研究中單組樣本量分別設定為20、30、50、100和200，以考察不同樣本量下檢驗方法的表現與檢驗效能。

(3)Hodges-Lehmann法

(1)

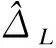
(U(Cα)，U[(n1×n2)+1-Cα])

(2)

其中Cα是一個小于等于置信區間下限的最大整數，表達為：

(3)

(4)Bootstrap可信區間法

Bootstrap方法最早由美國斯坦福大學統計學教授Efron[9]在1979年提出的。本研究中，在每種樣本含量下通過數學模擬產生500個Poisson分布樣本，并對每個樣本進行有放回、且樣本量不變的重復抽樣，獲得500個Bootstrap樣本，計算得到其中位數差值的置信區間。其具體步驟為：

①計算Poisson分布樣本數據的中位數M1、M2及M1-M2；

②對兩樣本分別進行有放回樣本例數固定的Bootstrap抽樣，獲得用于計算標準差的Bootstrap樣本；

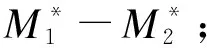
④重復②-③步驟500次，獲得500個Bootstrap樣本及500個中位數之差；

⑤置信區間計算方法：

L(M1-M2)B=(M1-M2)-ZαSE(M1-M2)B

(4)

b.Bootstrap百分位數法：用500個Bootstrap樣本獲得的500個中位數之差，并將中位數之差P2.5作為中位數之差的置信區間下限。

(5)檢驗結論及檢驗效能估計

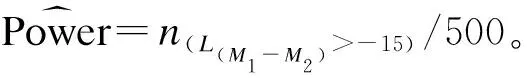
(6)軟件實現過程

通過SAS 9.4進行數據模擬，并完成兩種中位數差值的置信區間檢驗方法在非劣效性試驗中的比較。非劣效性檢驗中檢驗水準α設定為0.025。

結 果

1.H-L法、正態近似法和百分位數法95%置信區間的比較

H-L法的95%置信區間明顯比正態近似法波動范圍小，置信區間的寬度也要小于正態近似法，且每種方法的置信區間都包含中位數真實差異10h。同時，各組樣本量上H-L法置信下限的標準差均小于Bootstrap正態近似法和百分位數法。具體見表1和圖1。

表1 H-L法、正態近似法和百分位數法中位數差值95%置信下限的比較

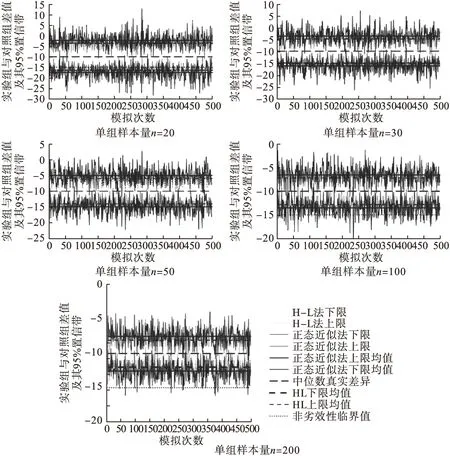
圖1 正態近似法和H-L法95%置信區間比較

2.三種方法的檢驗效能比較

三種方法的檢驗效能都隨著樣本增加而增加。在n=20時正態近似法和H-L法相當，但隨著樣本量的增大，H-L法均好于正態近似法和百分位數法。且在n≥100時，H-L法明顯好于正態近似法和百分位數法，而正態近似法和百分位數法相差不大。具體見表2和圖2。

表2 三種方法檢驗效能的比較[n(%)]

3.兩組受試者咽痛消失時間的比較

兩組受試者咽痛消失時間的比較中，三種檢驗方法的置信下限均大于非劣效性界值，均得出試驗藥非劣于對照藥的結論。但H-L法的置信區間最窄。具體見表3。

表3 兩組受試者咽痛消失時間差值及其95%可信區間(h)

討 論

本研究探討了兩種中位數差值的區間檢驗方法在非劣效試驗中的模擬比較研究。在樣本量為20時，正態近似法的檢驗效能和H-L法的檢驗效能相差不大。但隨著樣本量的增大H-L法的檢驗效能先是明顯高于正態近似法，在樣本量到200時，兩種方法的檢驗效能趨于一致。不論樣本量是多少，正態近似法的置信區間波動范圍都大于H-L法，且不如H-L法穩定，其原因可能和兩種方法利用樣本信息程度有關。H-L法充分利用每一個樣本信息，每一個觀測都要與另一組的每個觀測進行相減，且在后續計算中所占權重相等，并對極端值有較為穩健的處理[10]。而正態近似法則較多的考慮了原始樣本中位數的差異，其次，Bootstrap法還與原始樣本量有關，本研究中在單組樣本量為200時，正態近似法得到的置信區間波動范圍較樣本量為100時有了明顯改善，應注意的是在應用Bootstrap法估計中位數置信區間時是基于樣本很好地代表總體的假設[11]。

正態近似法和百分位數法的檢驗效能在樣本量大的時候趨于一致，但在小樣本時正態近似法明顯優于百分位數法。由于百分位數法單純的利用了Bootstrap樣本的P2.5和P97.5信息，其計算置信區間原理屬于一種非參數的方法，而正態近似法既利用了原始抽樣樣本中位數差值的真實差異又利用了Bootstrap樣本的信息，根據中心極限定理計算其置信區間屬于一種參數方法，故正態近似法的檢驗效能要優于百分位數法。臨床判斷非劣效性的一個重要問題是非劣效性界值Δ標準的選擇[12]。本研究中，當把非劣效性臨界值Δ設置為13、14時，三種方法的檢驗效能同時降低，但仍然是H-L法優于正態近似法和百分位數法。但由于H-L法的區間寬度最小且穩定，改變非劣效性臨界值對其影響較小。

本研究主要針對以時間作為效應指標，且可能存在不確切值的右截尾數據，并以中位數作為比較的指標進行非劣效性檢驗。除本研究介紹的兩類置信區間法外，也可以考慮選擇生存分析的方法。但理論上針對右截尾的數據中位生存時間和時間的中位數是相等的，而且如果仍采用Bootstrap法估計中位數差的置信區間結果與本研究中使用的方法也應該是一致。Jinheum指出也可以利用分層Cox比例風險模型計算中位生存時間差的置信區間[13]，但其標準誤計算較為復雜。因此，針對右截尾時間數據計算中位數差值的置信區間，應首先考慮基于中位數差的Bootstrap法或H-L法。但如果數據中存在其他類型的刪失數據，如研究對象中途退出等，此時中位數比較法已不再適用，應考慮利用分層Cox比例風險模型得到中位數差的置信區間。

從本次研究的結果來看，在藥物的非劣效試驗中，三種中位數差值的區間檢驗方法所獲得的區間都包含了總體中位數的真實差異。整體來看，H-L法獲得的區間最窄且最穩定，檢驗效能最高，且對極端值有較為穩健的處理，尤其在樣本量不大時建議選擇H-L法。其在實際應用中H-L法的操作復雜程度也要低于Bootstrap法。