融合信息技術突破數(shù)學建模教學環(huán)節(jié)的難點

摘? 要：數(shù)學建模探究活動要求學生能運用所學知識解決實際數(shù)學問題，體驗數(shù)學建模活動的完整過程.“茶水口感最佳問題”的教學要重點體現(xiàn)數(shù)據(jù)收集與處理，以及模型的選擇、檢驗和求解的過程.在難點的突破中，要注重引導學生利用信息技術探究、比較和分析多種模型的選擇方案.

關鍵詞：數(shù)學建模;信息技術;模型選擇

《普通高中數(shù)學課程標準（2017年版）》指出，數(shù)學建模是對現(xiàn)實問題進行數(shù)學抽象，用數(shù)學語言表達問題、用數(shù)學方法構建模型解決問題的素養(yǎng). 人教A版《普通高中教材·數(shù)學》（以下統(tǒng)稱“教材”）必修第一冊新增的數(shù)學建模案例“茶水口感最佳問題”就是一個很好的實例，體現(xiàn)了數(shù)學在人類生活、科學技術、社會發(fā)展中的應用. 同時，作為數(shù)學建模探究活動與學生初次接觸，引起了教師的廣泛關注，很多教學設計與反思都展現(xiàn)了數(shù)學建模案例的教學過程. 那么，這些教學設計是否都很好地突破了數(shù)學建模環(huán)節(jié)中的教學難點呢？這不免引起了筆者的思考.

一、“茶水口感最佳問題”教學難點突破中的問題

1. 教材情境呈現(xiàn)

情境：中國茶文化博大精深. 茶水的口感與茶葉類型和水的溫度有關. 經(jīng)驗表明，某種綠茶用85°C的水泡制，再等到茶水溫度降至60°C時飲用，可以產(chǎn)生最佳口感. 那么，在25°C室溫下，剛泡好的茶水大約需要放置多長時間才能達到最佳飲用口感？

顯然，如果能建立茶水溫度隨時間變化的函數(shù)模型，那么就能容易地解決這個問題. 為此，需要收集一些茶水溫度隨時間變化的數(shù)據(jù)，再利用這些數(shù)據(jù)建立適當?shù)暮瘮?shù)模型. 某研究人員每隔[1 min]測量一次茶水溫度，得到表1的一組數(shù)據(jù).

2.“選擇函數(shù)模型”教學難點與實際處理方式

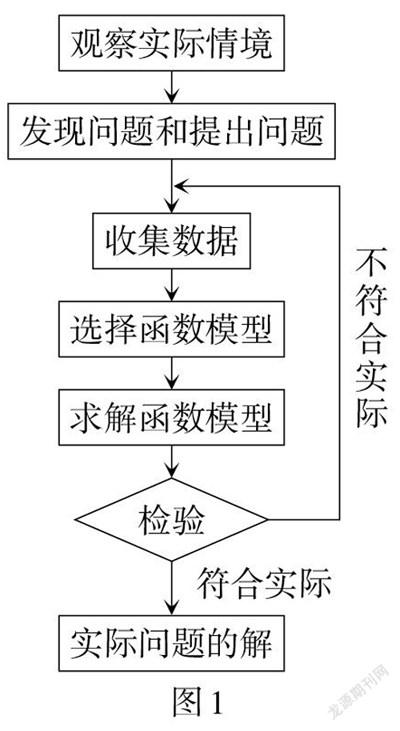
我們知道，建立函數(shù)模型解決實際問題的基本過程如圖1所示. 根據(jù)數(shù)學建模素養(yǎng)的內(nèi)涵，“茶水口感最佳問題”數(shù)學建模案例的教學重點可以設為將實際問題轉化為數(shù)學問題、數(shù)據(jù)的收集與函數(shù)模型的選擇和建立;教學難點可以設為數(shù)據(jù)的收集，函數(shù)模型的選擇. 而在實際教學中，數(shù)學模型的選擇卻在很大程度上被忽視，很

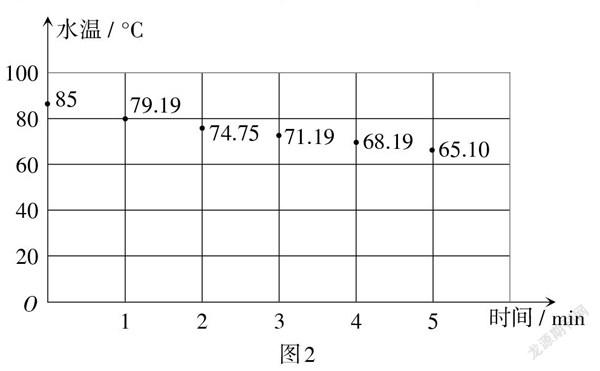
多教學過程都是“對照散點圖分布，考慮到茶水溫度降至室溫不能再降的事實”直接就確定函數(shù)模型為? [y=kax+25 k∈R，0<a<1，x≥0]. 因此，在接下來的模型求解中，得到表1對應的散點圖，如圖2所示. 同時，根據(jù)教材的處理方式，對表1進行處理，得到表2.

如果取[a]的平均值0.922 7，就可以得到函數(shù)模型[y=60×0.922 7x+25 x≥0]. 將數(shù)值代入，就可以得到[x≈6.699 7 min].

整個教學過程好像都是按照“事先既定”的數(shù)學模型進行求解，至于在收集數(shù)據(jù)和選擇模型的環(huán)節(jié)，學生“如何選擇模型”的教學過程呈現(xiàn)很少，甚至缺失.

3.“選擇函數(shù)模型”應關注的實際教學問題

本節(jié)課的編寫意圖及教學建議指出，通過觀察發(fā)現(xiàn)散點圖的分布狀況呈遞減狀態(tài)，學生可能會提出各種遞減函數(shù)作為備選模型. 教師應引導學生注意到茶水溫度降至室溫就不能再降這一重要事實，再結合幾類基本初等函數(shù)的變化特征，指導學生做出選擇. 需要注意的是，實驗所得的數(shù)據(jù)并不一定具有很強的規(guī)律性，函數(shù)模型的選擇也是多樣的，并不局限于指數(shù)型函數(shù)，所選擇的函數(shù)一般也只能大致反應茶水溫度變化的局部規(guī)律. 因此，建立模型后需要對模型進行檢驗. 教學建議還指出，建立模型與檢驗模型是實例教學的重點，除了教材提供的方法外，有條件的學校還可以指導學生利用信息技術工具選擇擬合功能建立模型，并利用相關系數(shù)檢驗吻合程度，幫助學生建立合適的函數(shù)關系式，然后利用特定參數(shù)值驗證模型，并解決實際問題. 因此，在“選擇函數(shù)模型”的實際教學環(huán)節(jié)，完全可以從信息技術與數(shù)學教學融合的視角，就以下問題進行深入思考.

問題1：除了指數(shù)函數(shù)模型，還有其他擬合模型嗎？如果有，與指數(shù)函數(shù)模型比較，擬合度分別怎么樣？

問題2：基于茶水溫度在降至室溫后就不能再降的事實，教學中如何引導學生進行模型選擇、比較和檢驗分析？

二、基于信息技術的模型選擇，突破教學難點

基于問題1，筆者就我們學習過的函數(shù)模型及散點圖來分析. 如果用線性模型、多項式模型或冪函數(shù)模型，與指數(shù)函數(shù)模型相比，誰的擬合度更高呢？采用不同的信息技術手段，對相關函數(shù)模型的擬合度進行了分析.

1. 采用WPS進行數(shù)據(jù)擬合

WPS有進行數(shù)據(jù)分析、算法的實現(xiàn)、函數(shù)模型擬合及圖象與性質(zhì)探究等功能，界面相對友好，操作方便，是教師和學生最熟悉的軟件之一，其中包含了大量的函數(shù)、公式.

首先，新建一張WPS表格，分兩列輸入時間和溫度數(shù)據(jù)（為了方便與上述函數(shù)模型對比，可以采用表2的數(shù)據(jù)處理）. 其次，選中數(shù)據(jù)區(qū)域，點擊“插入圖表”中的“[xy]散點圖”，然后點擊散點圖就會出現(xiàn)“圖表元素”項目，如圖3所示. 可以勾選“坐標軸”“數(shù)據(jù)標簽”“趨勢線”，在“趨勢線”下會有屬性欄“線性”“指數(shù)”“多項式”“冪”等選項，如圖4所示.

分別點擊“線性”“指數(shù)”“多項式”等選項，相應勾選“顯示公式”“顯示[R]平方值”，就會顯示圖4中的相關信息，得到線性模型[y-25=-3.887 4x+58.622]，[R2=0.982]，指數(shù)函數(shù)模型[y-25=59.053e-0.079x]，[R2=][0.993 5]，多項式模型[y-25=0.345 7x2-5.616x+59.774]，[R2=0.998 6]. 我們知道，在數(shù)學統(tǒng)計中，用[R2=1-][i=1nyi-y2i=1nyi-y2]來刻畫擬合效果，[R2]的值越大，擬合效果越好. 從而可知多項式模型的擬合效果最好. 其中，指數(shù)模型擬合與模型[fx=60×0.922 7x+25 x≥0]有些許差別，因為是信息技術工具通過估算得到的. 事實上，[e-0.079=0.924 04]，但是在WPS中不方便直接計算[fx=60×0.922 7x+25 x≥0]的擬合度. 另外，在散點圖中去掉[0，60]這個點后可以采用冪函數(shù)模型進行擬合，得到[y-25=55.248x-0.182，R2=0.962 8]. 因此，可以將通過上面各個模型得到的最佳飲用時間的[x]值列表，如表3所示.

從表3發(fā)現(xiàn)，四種模型的擬合度都十分不錯. 其中，雖然多項式模型的擬合度最高，但是在基于“60℃飲用口感最佳”的假設下最佳飲用時間不存在;冪函數(shù)模型達到最佳口感經(jīng)歷時間最長. 從數(shù)據(jù)來看，還不能完全回答問題1中的所有疑問. 因為基于WPS的數(shù)據(jù)分析，不能反映出各模型的函數(shù)圖象變化趨勢，也不能對原模型[fx=60×0.922 7x+25 x≥0]的擬合度進行估算. 因此，還需要借助GeoGebra軟件進行數(shù)據(jù)擬合再分析.

2. 采用“GeoGebra經(jīng)典”數(shù)據(jù)擬合

GeoGebra是一款十分重要的數(shù)學軟件. 它具有字母的邏輯運算、統(tǒng)計、微積分等功能，集幾何圖形、數(shù)據(jù)處理、代數(shù)運算于一體.

啟動“GeoGebra經(jīng)典6”，在表格區(qū)域輸入表2的數(shù)據(jù). 構造點列，軟件會將點列自動記為“[l]1”，圖形區(qū)域也會畫出散點圖. 在命令輸入欄輸入“指數(shù)擬合”，得到指數(shù)函數(shù)模型[y=59.053e-0.079x]. 在命令輸入欄輸入“可決系數(shù)[R]方[l1，f]”，得到關于[fx]的[R2]的值[0.993 5]. 繼續(xù)輸入函數(shù)模型[qx=60×0.922 7x]及“可決系數(shù)[R]方[l1，q]”，得到函數(shù)模型[y=60×0.922 7x+][25 x≥0]的[R2]的值[0.984 7]，如圖5所示. 同樣地，在命令欄分別輸入“多項式擬合[l1，1]”“可決系數(shù)[R]方[l1，h]”“多項式擬合[l1，2]”“可決系數(shù)[R]方[l1，g]”，就會得到線性模型和二次多項式模型. 去掉點[0，60]構造新點列[l2]，輸入冪函數(shù)擬合就會得到冪函數(shù)擬合模型，具體數(shù)值與WPS的數(shù)據(jù)都一致. 通過GeoGebra軟件不僅能方便地看到各個模型的擬合程度，還能了解每個模型的曲線形狀，如圖6所示. 從而一目了然地排除一些不符合實際條件的假設模型. 例如，二次多項式模型中最低點的值（即因變量的值）約不低于38°C;冪函數(shù)模型由于下降趨勢平穩(wěn)，長時間內(nèi)因變量的值可能不會低于20°C. 這就是表3中的二次多項式模型無解與冪函數(shù)模型時間長的原因，也充分說明了模型的選擇要與現(xiàn)實情況相結合，是對問題2的直觀回答.

3. 線性模型與指數(shù)模型的檢驗分析

根據(jù)情境假設，60℃是茶水飲用效果最佳的關鍵點. 教學中，教師和學生有必要思考在大于60℃這個高溫區(qū)間內(nèi)的數(shù)據(jù)檢驗與分析情況.

在選擇模型的過程中，如果缺少在大于60℃這個高溫區(qū)間內(nèi)對線性模型的分析與比較，就沒有很好地突破教學難點的表現(xiàn). 為什么這樣說呢？

首先，從表3中可以發(fā)現(xiàn)，線性模型與教材中估算得到的函數(shù)模型[y=60×0.922 7x+25 x≥0]的擬合度[R2]分別為0.982和[0.984 7]，得到最佳飲用時間分別為[6.077]和[6.699 7]，這兩個結果是十分接近的.

其次，我們知道，水在溫度較高時，溫度隨時間下降較快，當溫度接近室溫時，溫度下降越來越慢，從而在大于60℃這個高溫區(qū)間內(nèi)，結合采集的6組數(shù)據(jù)散點圖，學生很有可能采用線性模型進行求解.

最后，表2中的溫度和時間的數(shù)據(jù)線性相關性很強，不妨利用Excel（或WPS）中的“數(shù)據(jù)分析”進行線性回歸分析，如圖7所示.

圖7的數(shù)據(jù)表明，水在高溫區(qū)間（大于等于60℃）時，時間與溫度的線性相關系數(shù)為0.99，從而線性相關性是非常強的. 同時，[P=0.000 122<0.001]，說明線性回歸效果顯著性水平十分明顯，置信度達到99.9%以上. 這都說明有足夠的理由需要在大于60℃這個高溫區(qū)間內(nèi)對線性模型進行分析. 基于此分析，結合“茶水溫度在降至室溫就不能再降的事實”，比較之后選擇指數(shù)函數(shù)模型，教學過程更為自然.

三、反思與教學建議

用函數(shù)構建數(shù)學模型解決實際問題時，除了對變化過程中的常量、變量及相互關系進行分析之外，數(shù)據(jù)收集、數(shù)據(jù)處理和數(shù)據(jù)分析的過程也顯得尤為重要. 數(shù)學建模教學中包含復雜的數(shù)據(jù)采集與分析、多種建模求解方案的嘗試，是一個不斷探索、創(chuàng)新、完善和提高的過程. 那么，如何更好地開展高中數(shù)學建模探究活動教學呢？

1. 根據(jù)不同問題的相應特征收集盡可能多的數(shù)據(jù)

在組織學生開展數(shù)學建模活動時，需要根據(jù)不同問題的相應特征收集盡可能多的數(shù)據(jù). 教材中的案例給出了6組數(shù)據(jù)，在實際教學中還可以根據(jù)茶水冷卻時間的快慢收集更多數(shù)據(jù).

2. 引導學生進行不同數(shù)學模型的探究活動

不同的探究方向往往能觸發(fā)學生的創(chuàng)新思維，培養(yǎng)學生的創(chuàng)新意識. 因此，在解決問題的過程中，要引導學生進行不同數(shù)學模型的探究活動，讓學生經(jīng)歷不同數(shù)學模型對結果帶來的影響.

3. 選取能用確定的標準來衡量的實際問題

在數(shù)學建模教學初期選題時，盡量選取能用確定的標準來衡量的實際問題. 情境中所謂的“口感最佳”的數(shù)學本質(zhì)實際上就是計算溫度在60℃時建立的數(shù)學模型的函數(shù)值.

4. 引導學生了解要解決問題的相關背景

在數(shù)學建模教學時，要引導學生了解要解決問題的相關背景（如飲茶文化的相關知識）. 實際上，學生對飲茶文化的相關知識并沒有生活積累. 曾有國外專家研究，飲用65℃ ～ 69℃茶的人群，患食道癌的風險是飲用溫度低于65℃茶者的2倍;再有研究表明，食道的黏膜只能耐受50℃ ～ 60℃的溫度，超過這個溫度范圍就會被燙傷，而60℃恰好處于臨界點.

在數(shù)學建模教學時，還要注重與信息技術的融合. 信息技術能提高學生學習數(shù)學的興趣和應用數(shù)學的意識與能力，盡量引導學生利用熟悉的數(shù)學軟件及WPS處理數(shù)據(jù)的意識，將數(shù)學、計算機有機地結合起來，解決實際生活中的問題.

參考文獻：

[1]中華人民共和國教育部制定. 普通高中數(shù)學課程標準（2017年版）[M]. 北京：人民教育出版社，2018.

[2]周威. 例談回歸分析在學校評價中的實際應用[J]. 中學數(shù)學，2015（5）：49-50.

收稿日期：2021-06-23

基金項目：湖北省教育科學規(guī)劃課題——基于課程標準的教學與質(zhì)量測評研究（2020JB348）;

恩施州教育科學規(guī)劃課題——區(qū)域教研中推進高中數(shù)學教師踐行課程標準的教學與質(zhì)量測評研究（ZGH202045）.

作者簡介：周威（1985— ），男，中學一級教師，主要從事高中數(shù)學教研與質(zhì)量測評研究.