無限長載流薄板磁場的矢勢與磁感應(yīng)強(qiáng)度計算及可視化*
周群益
(廣州理工學(xué)院 廣東 廣州 510540)
莫云飛
(長沙學(xué)院電子信息與電氣工程學(xué)院 湖南 長沙 410022)
周麗麗
(贛南醫(yī)學(xué)院信息工程學(xué)院 江西 贛州 341000)
侯兆陽
(長安大學(xué)理學(xué)院應(yīng)用物理系 陜西 西安 710064)
1 引言
求無限長均勻通電薄板的磁場是電磁場理論中的一個典型習(xí)題,一般教材只計算中垂面或(和)板平面上的磁感應(yīng)強(qiáng)度[1],有的習(xí)題解答計算了全部空間的磁感應(yīng)強(qiáng)度[2,3],其根據(jù)是無限長直線電流的磁感應(yīng)強(qiáng)度公式和場強(qiáng)疊加原理.但這些教材和習(xí)題解答沒有圖像,也沒有對結(jié)果進(jìn)行分析.本文根據(jù)無限長直線電流磁場的矢勢公式和矢勢疊加原理求薄板電流磁場的矢勢,再利用磁感應(yīng)強(qiáng)度與矢勢的關(guān)系簡單地求出磁感應(yīng)強(qiáng)度,并將公式無量綱化,計算和繪制了矢勢和磁感應(yīng)強(qiáng)度的分布曲面以及二維磁感應(yīng)線,充分顯示了磁場的分布規(guī)律.
2 薄板電流磁場的矢勢
無限長直導(dǎo)線通有電流I,其磁場矢勢的方向與電流方向相同,大小為[4]
(1)
其中,R是場點(diǎn)到直線電流的距離,R0是矢勢零點(diǎn)到直線電流的距離.
設(shè)薄板的寬度為2L,電流為I,則面電流的線密度
如圖1所示,在直角坐標(biāo)系Oxyz中電流方向沿著z方向(垂直紙面向外),矢勢A和磁感應(yīng)強(qiáng)度B的分布與坐標(biāo)z無關(guān).
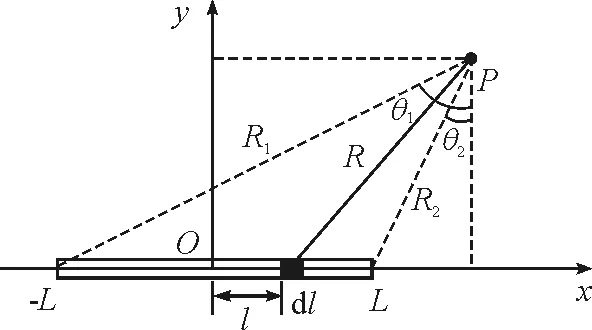
圖1 無限長通電薄板的截面和磁場的矢勢
取Oxy截面,在距離為l處取長度dl,那么,電流元為
dI=jdl
場點(diǎn)P(x,y)到電流元dI的距離為
(2)
電流元在點(diǎn)P產(chǎn)生磁場的矢勢大小為
薄板電流在點(diǎn)P產(chǎn)生磁場的矢勢大小為
(3)
利用分部積分法可得
2y(arctank2-arctank1) + 4L+ 4LlnR0]
(4)
其中
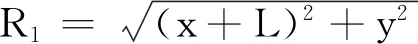
(5)
(6)
這里,R2和R1分別是場點(diǎn)P到薄板右端和左端的距離,k2和k1分別是角度θ2和θ1的正切.取(0,0)為矢勢零點(diǎn),可得
lnR0=lnL-1
(7)
因此
(8)
當(dāng)x=0時,可得中垂面上的矢勢大小
(9)
當(dāng)y→0時,可得板平面上的矢勢大小
(10)
當(dāng)x=0時,可得原點(diǎn)處的矢勢A(0,0) = 0.
3 薄板電流的磁感應(yīng)強(qiáng)度
根據(jù)矢勢的旋度可求磁感應(yīng)強(qiáng)度
B=▽×A
(11)
在直角坐標(biāo)系中可得
分量為
(12)
將式(4)代入上式,可得磁感應(yīng)強(qiáng)度的兩個分量
(13)
(14)
合磁感應(yīng)強(qiáng)度大小為
(15)
方向由角度確定
(16)
討論:(1)當(dāng)x= 0時,由式(13)、(14)可得中垂面上磁感應(yīng)強(qiáng)度的兩個分量
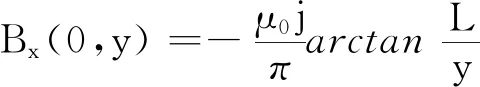
(17)
當(dāng)y→±0時,可得原點(diǎn)處的磁感應(yīng)強(qiáng)度
(18)
(2)當(dāng)y→0時,由式(13)、(14)可得板平面上磁感應(yīng)強(qiáng)度的兩個分量
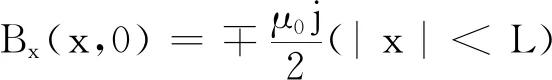
(19)
(20)
(3)當(dāng)L→∞時,由式(13)可得

(21)
由式(14)可得
(22)
說明無限大薄板電流在兩邊產(chǎn)生的是勻強(qiáng)磁場.
(4)當(dāng)|x|?L且|y|?L時,由式(13)可得
(23)
由式(5)可得
將R1和R2代入式(14),可得
(24)
將Bx和By代入式(15),可得
(25)
這是無限長直線電流產(chǎn)生的磁感應(yīng)強(qiáng)度公式.
4 磁場公式的無量綱化
取L作為坐標(biāo)單位,則
二者均為無量綱的坐標(biāo).取
為矢勢的單位,將式(7)代入式(1),可得直線電流磁場的無量綱的矢勢
(26)
其中
薄板電流磁場的無量綱的矢勢為
arctank2-arctank1)
(27)
其中
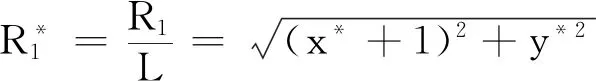
(28)
(29)
同理可得中垂面和板平面上無量綱的矢勢.
設(shè)
顯然
取B0作為磁感應(yīng)強(qiáng)度的單位,則無量綱的磁感應(yīng)強(qiáng)度分量分別為
(30)
(31)
無量綱的合磁場大小和方向分別為
(32)
同理可得中垂面和板平面上無量綱的矢勢和磁感應(yīng)強(qiáng)度的分量.
5 磁場的可視化
(1)無限長薄板電流在中垂面上磁場的矢勢Az(0,y)的曲線如圖2(a)所示,Az(0,y)是y的偶函數(shù),離板越近,矢勢越高,y= 0處是一個尖點(diǎn);當(dāng)|y|很大時,其矢勢接近于直線電流磁場的矢勢.中垂面上的磁場Bx(0,y)的曲線如圖2(b)所示,中垂面上的磁場分量By(0,y)=0,而分量Bx(0,y)是y的奇函數(shù),說明薄板兩邊磁場的方向相反,離板越近,磁場越大.磁場在y=0處發(fā)生跳躍,這是因?yàn)锳z(0,y)在此處是尖點(diǎn).當(dāng)|y|很大時,其磁場接近于直線電流產(chǎn)生的磁場.
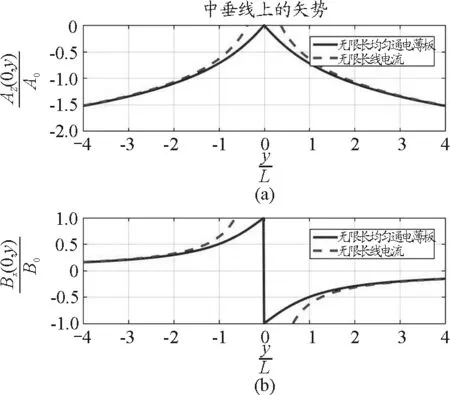
圖2 無限長均勻通電薄板中垂面上的矢勢和磁場
(2)薄板電流在板平面磁場的矢勢Az(x,0)的曲線如圖3(a)所示,Az(x,0)是x的偶函數(shù),軸心的矢勢最高;在板的邊緣x=±L處的矢勢是拐點(diǎn),當(dāng)|x|很大時,其矢勢接近于直線電流磁場的矢勢.板平面上的磁場By(x,0)的曲線如圖3(b)所示,By(x,0)是x的奇函數(shù),板內(nèi)磁場是單調(diào)上升的曲線,板外磁場是單調(diào)下降的曲線,板的邊緣x=±L處的磁場在理論上是無窮大;當(dāng)|x|很大時,其磁場接近于直線電流產(chǎn)生的磁場.
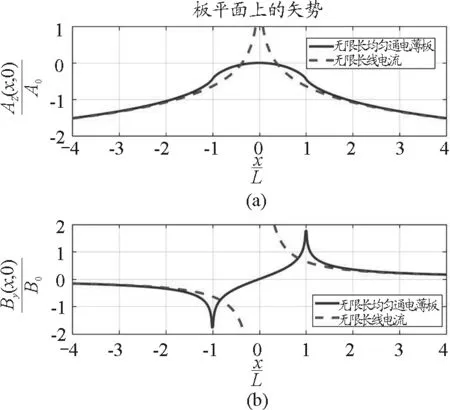
圖3 無限長均勻通電薄板平面上的矢勢和磁場
(3)薄板電流磁場的矢勢Az(x,y)分布面如圖4所示,點(diǎn)(0,0)的矢勢最高;中垂面上的矢勢Az(0,y)的曲線和板平面上的矢勢Az(x,0)的曲線分布在曲面上.
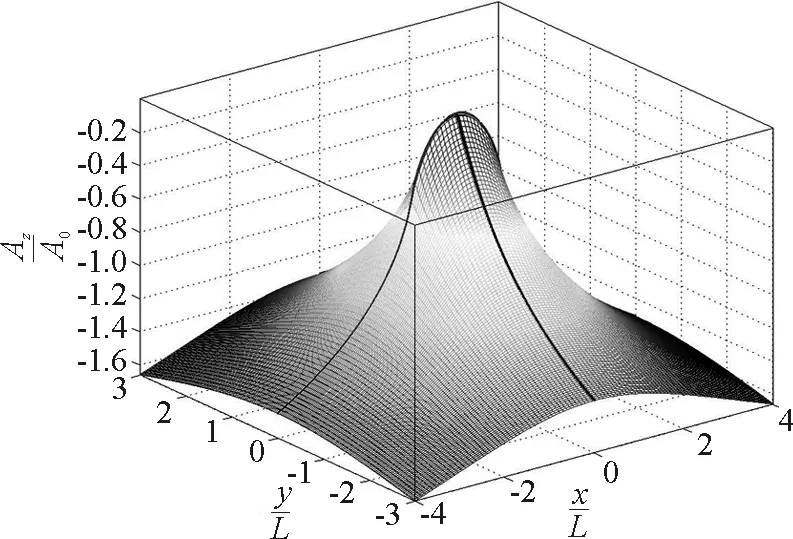
圖4 無限長均勻通電薄板磁場的矢勢分布面
(4)薄板電流磁場的x分量Bx(x,y)的曲面如圖5所示,Bx有一個“峭壁”,位于薄板所在處,在板的表面(x,0+),磁場為-B0;在板的表面(x,0-),磁場為B0.
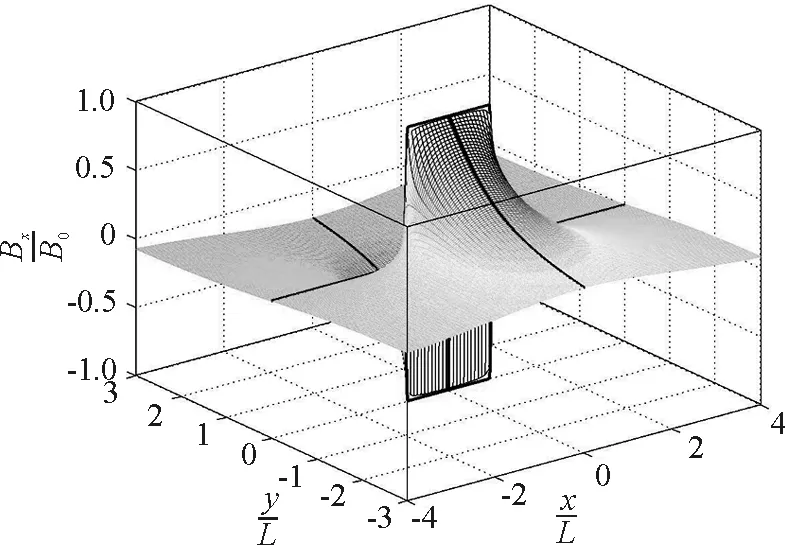
圖5 無限長均勻通電薄板磁場的x分量分布面
(5)薄板電流磁場的y分量By(x,y)的曲面如圖6所示,By有一對對稱的“峰”和“谷”,這是薄板邊緣的By,(±L,0)處的By在理論上是無窮大.
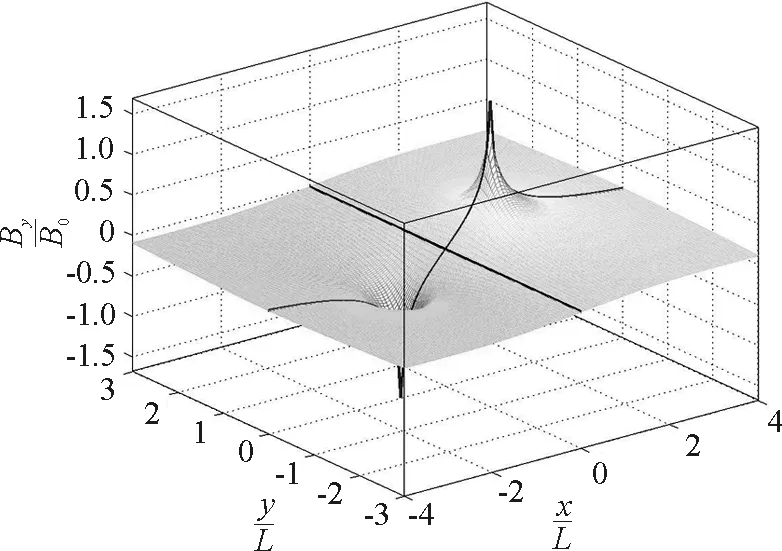
圖6 無限長均勻通電薄板磁場的y分量分布面
(6)合磁場B(x,y)的曲面如圖7所示,點(diǎn)(0,0)是B的一個鞍點(diǎn).B有一對犄角,說明薄板邊緣的磁場在理論上是無窮大.
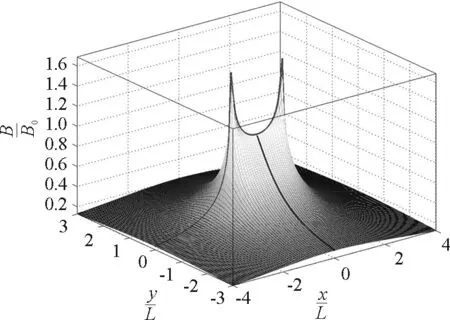
圖7 無限長均勻通電薄板合磁場的分布面
(7)合磁場B的方向角α(x,y)曲面如圖8所示,α隨著極角的增加而增加.在x=0,y>0的正軸上,α發(fā)生從π到-π的躍變;在y= 0,-L 圖8 無限長均勻通電薄板磁場方向的分布面 (8)薄板電流磁場在截面上的磁感應(yīng)線如圖9所示,在薄板附近,磁感應(yīng)線比較密集,磁場比較強(qiáng);離板越遠(yuǎn),磁感應(yīng)線越稀疏,磁場越弱;遠(yuǎn)處的磁感應(yīng)線接近于圓. 圖9 無限長均勻通電薄板的磁感應(yīng)線 本文建立了均勻通電薄板在直角坐標(biāo)系中的矢勢和磁感應(yīng)強(qiáng)度公式,通過無量綱化處理,解決了有關(guān)的計算和可視化的問題.如果將這種方法解決均勻帶電薄板的電勢和電場強(qiáng)度的問題,將發(fā)現(xiàn)兩個問題的解答和圖片有許多相似之處.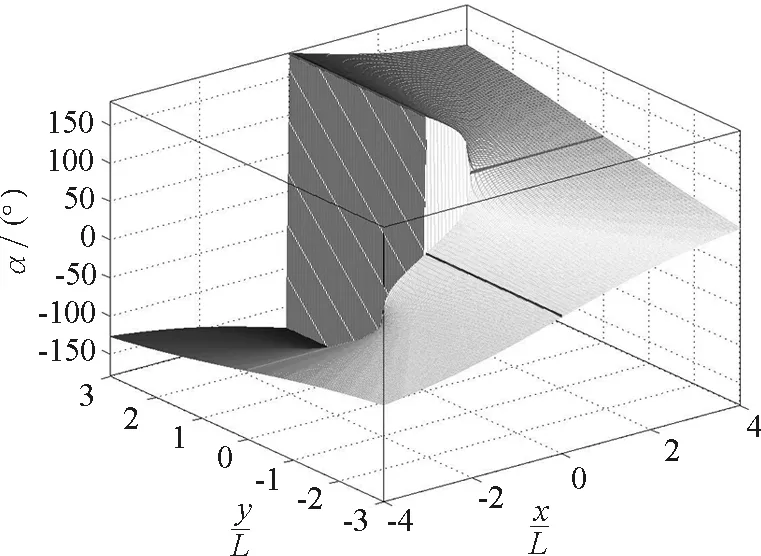

6 結(jié)束語

