深水測試管柱與隔水管的橫向承載特性

孫巧雷 李 中 王爾鈞 馮 定 陳文康 劉統亮 嚴淳鳀

1.長江大學機械工程學院 2.湖北省油氣鉆完井工具工程技術研究中心 3.中海油研究總院有限責任公司

0 引言

海上測試作業是進行海洋油氣勘探開發、儲層評價的基礎，能為海洋油氣的高效開采提供直接依據[1-2]。海上測試作業過程中，測試管柱位于隔水管內部，隔水管通過張緊裝置與平臺連接，測試管柱懸掛在頂驅大鉤上，海水、隔水管、環空流體、測試管柱及管內流體組成了海上測試的“管中管”結構體系[3-6]。由于風、波浪、海流等環境載荷的激勵，測試水深的增加，深水測試作業易導致隔水管與測試管柱產生復雜的橫向動態特性，從而引起測試管柱的彎曲、碰撞、磨損等。

此前，在海上管柱力學方面，國內外研究主要圍繞隔水管下入、立管渦激振動、隔水管與井口的耦合作用等方面[7-15]，而測試管柱力學研究則主要集中在地層段[16-17]，近幾年海水段的研究才逐漸增多。唐海雄等[18]結合海上高溫井測試特性，進行了溫度對測試管柱伸縮變化量的研究；謝鑫等[19]應用有限元法，進行了波浪載荷作用下的管柱動力響應分析；楊志等[20]通過建立井筒溫度預測模型，進行了深水測試水深變化下循環液溫度的變化規律分析；結合深水測試過程，劉康等[21-23]、楊紅君等[24]對測試密封插管安全長度的確定、測試作業的運作模式與測試技術、管柱螺紋連接密封、開關井管柱的安全窗口等進行了研究；何玉發等[25]應用Abaqus軟件，開展了深水測試管柱的優化研究；劉紅兵等[26]通過建立隔水管—測試管柱渦激振動模型，對渦激振動機理、疲勞損傷規律等展開了研究。但現有的測試管柱相關研究主要是集中測試管柱的工藝、管柱連接安全、天然氣水合物等方面[27-28]，少有針對隔水管—測試管柱組成的結構進行橫向承載特性分析。

筆者針對我國南海測試使用“管中管”體系結構及作業水深超過900 m的特點，建立了考慮內外流體影響下的測試管柱及隔水管橫向動態受力模型；應用數值求解方法，研究了隔水管張緊力、測試管柱懸掛力、海流流速及平臺漂移量對“管中管”結構橫向承載參數的影響，以期為海上安全測試作業的控制提供理論支撐。

1 海水段井筒溫壓及軸向力計算模型

井筒溫度、壓力及管柱軸向力分布是進行測試管柱橫向承載特性分析的前提，針對海水段多立管的溫壓場計算，眾多學者已開展了研究[29-32]，筆者結合已有的研究成果，應用傅里葉傳熱定律、多層圓管傳熱特性、能量守恒方程，建立了海上測試作用海水段井筒的溫壓場計算模型；結合測試管柱多變截面、內部流體流動等特性，建立了海水段測試管柱軸向力計算模型。

1.1 井筒溫度場模型

測試作業海水段的井筒位于泥線以上，測試管柱內部流體與海水間經油管、環空測試液、隔水管進行換熱，井筒結構及其剖面如圖1所示。為了簡化溫度場的計算，分析前作如下基本假設：①忽略測試管柱內部流體及環空流體軸向熱傳導，即僅考慮徑向上的傳熱；②測試作業內部流體、環空流體及其海域的海水溫度場是連續的；③測試管柱內部天然氣及環空測試液為一維穩態流動及傳熱，管柱簡化為等截面體；④內部流體無逃竄，環空流體充滿。

圖1 海水段測試管柱井筒剖面圖

基于以上假設，管內流體微元與環空流體微元換熱量Qia、環空微元與海水微元的換熱量Qas方程為：

式中ma表示環空流體質量流量，kg/s；ca表示環空流體的比熱，J/(kg·℃)；Ti表示測試管柱內流體的溫度，℃；Ta表示環空流體的溫度，℃；Tsea表示海水溫度，℃；A、B表示中間變量，；Ro表示隔水管外徑，m；ro表示測試管柱外徑，m；Ui表示管柱內流體與環空間傳熱系數，W/(m2·℃)；Ua表示環空流體與海水的傳熱系數，W/(m2·℃ )。

對于流體微元的流動，應用能量守恒方程，可得到環空流體及管內流體微元的控制方程，然后通過高斯消元法及齊次微分方程的求解，可獲得管內流體溫度的解析解：

其中

式中a、b分別表示待求量，C、D、E、r1、r2分別表示中間量；mi表示管內流體質量流量，kg/s；CJ表示環空流體的焦湯系數，CJi表示管柱內流體的焦湯系數，ci表示管內流體的平均比定熱容，J/(kg·℃)；va表示環空流體流速，m/s；vi表示管內流體流速，m/s；θ表示微元段中心軸線與z軸（垂直于地心）間的夾角，（°）；pi表示管內流體壓力，Pa；pa表示環空流體壓力，Pa。

該模型的求解需結合井筒壓力場及泥線處的環空溫度與管內溫度進行求解。

1.2 井筒壓力場模型

1.2.1 環空測試液壓力場

對于測試過程中環空流體的壓力，忽略壓力對液體性能的影響，簡化條件的環空流體壓力可按下式計算：

式中ρfo表示環空流體密度，kg/m3；L表示水深，m；p0表示環空井口處壓力，Pa。

1.2.2 測試管柱內部流體壓力場

由于當前我國深水測試主要以氣井為主[33-34]，在考慮內部天然氣特性的基礎上，可通過分段求解內部流體的壓力：

式中pout表示微元段出口壓力，Pa；pin表示微元段進口壓力，Pa；，qsc表示管內流體當量產量，m3/d；，γg表示管內流體密度，kg/m3；K表示中間變量，，Kin、Kout分別表示進出口計算參數；λ表示管內流體與油管間的流動摩阻系數。

1.3 測試管柱軸向力計算模型

測試作業時，考慮內外流體、截面效應、彎曲效應等對管柱軸向力的影響[35]，忽略測試管柱軸向與橫向的方向的夾角，則深度距泥線處zm處t時刻海水段測試管柱單元的軸向力為：

式中To(t)表示的大鉤懸掛力，N；We(z,t)表示測試管柱有效浮重，N；表示內外流體壓差產生的虛構拉力，N；Ff(z,t)表示內外流體沿管體軸向流動產生的摩擦阻力，N；Fv表示管柱內外變截面引起的附加力[35]，N ；表示管柱橫向彎曲產生的附加軸向力，N；ρfo和ρfi分別表示管內、管外流體的密度，kg/m3；Aro和Ari分別管外部、管內部的截面積，m2；As表示管柱有效截面積，m2；g表示重力加速度，一般取9.81 m/s2。

2 “管中管”結構理論模型建立

2.1 管柱微元力學平衡方程

圖2 測試管柱微元受力圖

海上測試過程中，隔水管和測試管柱的內外壁均與流體相互作用，對于穩定流動下的管柱受力，以測試管柱微元段為例進行受力分析，如圖2所示。假設單元為小變形量時，以管柱中心為原點，管柱中點的傾角為，管柱端面的力包括軸向力T、彎矩M、和剪力N，以及內外流體及隔水管對測試管柱微元的橫向作用合力為Fx、軸向作用的合力為Fz，管柱重力We。根據單元水平方向上的力學平衡方程，可得：

在小變形的假設下，忽略二階小量，即認為，

結合材料力學剪力、彎矩、曲率與變形間的關系[36-37]，可得：

式中E表示測試管柱的彈性模量，Pa；I表示測試管柱慣性矩，m4；Fo(z,t)表示管柱單元的橫向綜合載荷。

在考慮管柱內外流體慣性力、管柱慣性力、管柱與流體相互作用的橫向摩阻分量、隔水管與測試管柱相互作用力、管柱阻尼，管柱微元的橫向綜合載荷Fo(z,t)可表示為：

將式（9）代入式（8），最終獲得考慮測試管柱與內外流體間相互作用的橫向動態微分方程為：

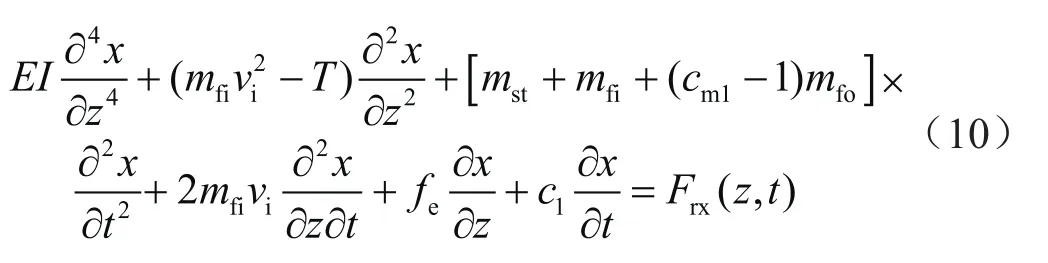
2.2 隔水管橫向微分方程

對于測試作業的“管中管”結構體系，分別以隔水管與測試管柱微元為研究對象，建立其力學平衡方程。基于上述測試管柱微元的受力分析，隔水管與其內外流體的橫向耦合作用動態微分方程為：

式中Er表示隔水管的彈性模量，Pa；Ir表示隔水管的慣性矩，m4；mfo表示單位長度環空流體質量，kg；mr表示單位長度隔水管質量，kg；vo表示環空流體流速，m/s；c2表示隔水管粘性阻尼系數；Tr表示隔水管軸向力分布，N。

2.3 海水對隔水管作用力

波浪力和海流力的載荷計算可應用莫里森方程表達[38]：

式中De表示隔水管外徑，m；vc表示海流引起的水質點橫向速度，m/s；vw表示波浪引起的水質點橫向速度，m/s；表示波浪引起的水質點橫向加速度，m2/s；CD表示拖拽力系數，取值范圍介于0.6～1.2；CM表示慣性力系數，取值范圍介于1.5～2.0。

3 模型定解條件與求解方法

3.1 模型求解方法

在產量測試過程中，由于環空流體不循環，因體積變化下的相對流速也較小，此時可忽略環空測試液的牽連慣性力、科氏慣性力，則測試過程中的隔水管與測試管柱構成的管柱體系的耦合受力模型為：

式（13）即為測試作業過程中“管中管”結構隔水管與測試管柱的橫向動態受力模型，在隔水管與測試管柱整體產生穩定的橫向變形時，此時可將上式聯立進行求解。求解前，式中微分方程可應用差分法進行求解，此外還需對整個時間與空間內的求解域進行網格離散，如圖3所示。

圖3 求解網格離散圖

在求解域內，各階導數的計算可用積差表達：

式中ΔL表示空間網格長度，m；Δt表示時間網格長度，s。

同時，在分析計算時，周期性載荷變化下可認為管柱的橫向變形具有周期性，即

3.2 模型定解條件

對于測試管柱與隔水管的邊界情況，測試管柱上端與平臺的大鉤相連，下端通過插入式懸掛器與水下井口頭連接，在上部補償情況下，懸掛器可產生小幅轉動；隔水管上端與張緊器連接，下端也與水下井口連接，兩者下端均可視為鉸接，上端可隨平臺存在一定的漂移[39]。在進行模型求解時，主要分析測試管柱與隔水管的最大承載特性，忽略時間域的影響，并假設兩者的最大橫向承載一致，其下端邊界條件可表示為：

上端的邊界條件為：

4 實例分析

4.1 相關基本參數

以我國南海已完成測試的某A井為例，該井是典型的深水井，水深為975 m，隔水管設計的初始頂張力大于隔水管柱串的浮重，隔水管與測試管柱的環空流體密度為1 300 kg/m3，作業期間的平均波浪周期約為6 s，波高2.2 m，表層海流速度為0.35 m/s，隔水管外徑為533.4 mm，測試管柱外徑為114.3 mm，產量為100×104m3/d時，基于井筒溫壓分布的計算結果，海水段測試管柱內部平均溫度為315 K，平均壓力為21.95 MPa，對應壓縮因子取0.86，計算得管內天然氣的平均密度為161 kg/m3，流速為8.37 m/s。對比不同模型下的軸向力計算結果如圖4所示，圖中考慮內外徑及油管浮重、僅考慮油管浮重下的計算沒有考慮溫壓的影響。

圖4 考慮不同因素下軸向力計算結果圖

將上述兩種結果與考慮溫度壓力特性下的測試管柱軸向力結果進行對比可知，水深越深，兩者的差值越大，由式（10）可知，軸向力的差異性勢必引起管柱受力特性的變化，因此，在后續分析中，筆者將考慮溫壓、浮重、變徑及內流摩阻下管柱軸向力模型作為橫向動態受力模型求解和承載分析基礎。

此外，隔水管、測試管柱作為整體穩定變形時，認為測試管柱、隔水管的位移、轉角一致，彎矩變化規律相同。對于海上測試管柱與隔水管的等效應力，可應用第四強度理論進行計算，等效應力σc可表示為：

式中σz表示管柱的軸向應力；σρ表示管柱的徑向應力；σφ表示管柱的環向應力。

根據相關研究結果[35,40]，隔水管與測試管柱的等效應力隨著軸向應力的增大而增大；同時由式（6）以及軸向應力公式和彎矩計算公式，在管柱截面慣性矩一定情況下，彎矩的增長能反映管柱軸向應力的增長，即彎角、彎矩的增大，管柱的軸向應力也增大。在管柱周期性橫向變形下，橫向位移、彎角、彎矩的增大會導致管柱周期性應力的增大，從而減小管柱的疲勞壽命。因此，本文以隔水管—測試管柱組成的管柱體系的最大位移、最大轉角、最大彎矩作為管柱體系橫向承載特性進行分析[41]。

4.2 頂張力與懸掛力影響

以隔水管實際重力G為基準，分析頂張力為1.2 G、1.4 G、1.6 G、1.8 G下的橫向承載，得到不同頂張力作用下管柱體系的橫向最大位移、最大轉角、最大彎矩如圖5所示。在A井測試管柱坐掛懸掛力為1 066 kN的基礎上，以1 066 kN懸掛力波動±20%內進行分析，獲得的不同懸掛力下的管柱橫向承載參數如圖6所示。

由圖5、6可知，隨著隔水管頂張力、測試管柱懸掛力的增加，隔水管與測試管柱體系各水深處的最大位移、最大轉角、最大彎矩均減小；在海平面至泥線100 m處附近，各水深處管柱體系的最大位移、最大轉角、最大彎矩的絕對值隨頂張力、懸掛力的增大而減小，靠近泥線處相關參數隨頂張力、懸掛力增大而增大；在海平面至泥線100 m以上，各水深處的彎矩絕對值隨著頂張力、懸掛力的增大而減小，泥線處附近彎矩隨著頂張力、懸掛力的增大而增大。

圖5 頂張力變化下隔水管—測試管柱體系的最大橫向位移、轉角和彎矩圖

圖6 懸掛力變化下隔水管—測試管柱體系的最大橫向位移、轉角和彎矩圖

在隔水管頂張力、測試管柱懸掛力變化時，橫向承載相關參數隨水深的變化趨勢基本一致，增加隔水管頂張力、測試管柱懸掛力均有助于減小管柱體系的最大橫向位移，同比例增加頂張力的效果更明顯。測試作業增加隔水管的頂張力有助于增加隔水管的橫向剛度及振動阻尼、從而減小管柱體系的橫向位移、轉角及彎矩，在橫向最大位移減小的基礎上，管柱的振動應力幅值及大小也會有一定的減小[42]。但由于隔水管的張緊力過大也會導致其自振頻率、軸向應力的增加，影響隔水管的抗疲勞[43]，因此隔水管的頂張力也不宜過大。

同時將上述結果與隔水管、測試管柱分別受相同海洋環境載荷時的結果進行對比，如圖7所示。根據圖7相關結果可知，管柱的最大位移、最大轉角、最大彎矩在僅考慮隔水管時要大于考慮隔水管—測試管柱體系的值；將海洋環境載荷直接作用于測試管柱時，測試管柱的相關參數要小于管柱體系值，主要是由于海流與波浪對測試管柱截面的作用力、測試管柱的慣性矩等都減小；但對于管柱體系下的測試管柱而言，計算的測試管柱彎矩比將海洋環境載荷直接作用于測試管柱時的彎矩小，因此，將海洋載荷直接作用于測試管柱進行測試管柱力學分析與測試管柱位于隔水管內部的實際工況有較大差別。

圖7 相同海洋環境載荷下立管的最大橫向位移、轉角和彎矩圖

4.3 波浪影響

根據A井作業海域海流參數的統計數據，分析作業區域常規流速、最大流速及不同年限周期所遇最大流速下的管柱體系的橫向承載特性，相關海流參數如表1所示，通過計算得到不同海流流速下的隔水管—測試管柱體系的橫向承載參數如圖8所示。

由圖8結果可知：當測試海域海流由0.35 m/s增加到2.27 m/s時，管柱體系各水深處的最大橫向位移、轉角、彎矩有明顯增加，整個管柱參數出現極值點的水深均一定程度上增大，這是由于泥線處海流流速不為0，海流隨水深的變化率增大。從總體上看，海流流速對管柱體系的橫向承載參數作用明顯，測試作業海域海流流速的增加，加大了管柱體系失效的風險，因此，在實際測試作業時一般會根據相關監測的相關海域的海洋環境載荷優選時間，同時現場測試作業也需密切監測作業海域的海流流速，以便應對潛在的風險。

表1 A井海域海流流速統計參數表 單位：m/s

4.4 平臺漂移影響

由于海洋環境載荷的作用，鉆井平臺在測試過程中可能會產生一定的漂移，以A井水深5%范圍的5 m、10 m、20 m、30 m、50 m的偏移量進行“管中管”結構體系橫向承載特性的研究，相關結果如圖9所示。

由圖9結果可知，管柱體系的最大位移隨著平臺漂移量的增加顯著增加，管柱體系的最大橫向位移幅值逐漸靠近海平面；最大轉角及彎矩幅值隨著平臺漂移量的增加，先減小后增大；主要是由于海流作用使管柱和平臺會產生一定程度的橫向偏移量，要使平臺井口與水下井口對中或作業超過平臺自然橫向偏移量，均會導致管柱上端懸掛處的彎矩和轉角增大；因此，就管柱的理論最大彎矩和轉角而言，在測試作業時，順海流方向使平臺產生的合理偏移，會使管柱體系彎角和彎矩減小，在一定程度上能改善管柱體系的承載，以A井為例，平臺漂移量為10～20 m間有助于改善測試橫向承載。

圖9 漂移量變化下隔水管—測試管柱體系的最大橫向位移、轉角和彎矩圖

5 結論

1）通過分析海上測試管柱海水段井筒溫度傳遞過程、傳熱特性，考慮測試管柱內外流體壓力的影響，建立了海上測試作業井筒的溫壓場模型；結合測試管柱內外多變徑引起的截面效應、流體流動引起的摩阻效應、彎曲作用產生的附加軸向力等影響，建立了海水段測試管柱的軸向力模型。

2）基于管柱微元的受力模型，考慮內外流體流動下的慣性力、摩阻力、管柱結構慣性力、阻尼等建立了管柱微元的橫向受力平衡方程；結合海水、隔水管、環空流體、測試管柱、管內流體構成的海上測試“管中管”結構特點，建立了“管中管”結構隔水管和測試管柱的橫向動態受力模型，并結合其邊界條件，對模型的求解方法及定解條件進行了確定。

3）基于建立的理論模型，在假設隔水管與測試管柱共同產生橫向變形的基礎上，分析了海上測試作業過程中測試管柱懸掛力、隔水管頂張力、海流及平臺漂移量對管柱體系橫向承載參數的影響，相關結果表明：增加隔水管頂張力、測試管柱懸掛力均有助于減小管柱體系的橫向承載參數，同比例幅度增加隔水管的頂張力、測試管柱懸掛力，頂張力對管柱橫向承載參數的影響更明顯；海流流速的增加使得管柱體系的最大橫向位移、轉角、彎矩增大明顯；順著海流方向平臺產生合理的漂移量有助于減小管柱體系的轉角及彎矩，以A井為例，10～20 m的平臺漂移量為宜。