深水區地震資料處理變參數振幅恢復技術

陳殿遠 劉仕友 孫萬元

中海石油（中國）有限公司湛江分公司

0 引言

處理中的變參數振幅補償技術，有效地解決了淺水—坡折帶—深水區域資料的保幅性問題。

現今油氣勘探的重點領域逐漸轉向深水區油氣藏，從海洋地震資料中可以發現，深水區的地震資料存在諸多問題[1-3]。目前，大多數技術手段都是假設地下介質近似水平層狀，未考慮海水的物理特征以及大陸坡折帶地區的實際情況。在淺水地震資料處理中，往往可忽略海水的聲學性質，然而在深水地震勘探中，海水深度介于1 000～3 000 m，海水的聲學性質也明顯不同于巖石，地震波在海水中的傳播速度（以下簡稱海水速度）具有明顯的分層性[4-6]。宋洋等[7]提出利用地震剖面獲取海水層溫度、鹽度、密度等物理參數，證明海水非單一均勻介質。韓復興等[8-9]從影響海水速度變化的主要因素（海水溫度、鹽度和深度）的經驗公式出發，建立海水速度模型，分析討論了海水速度變化對地震波走時、射線路徑及振幅的影響。Berryhill[10]首次針對崎嶇海底提出波動方程解決思路，鄧盾等[11-12]從疊前深度域保幅偏移算法、雙方位地震資料聯合成像兩方面對崎嶇海底成像進行研究。

另一方面，海水不是理想的無損耗介質，當聲波在海水中傳播時，隨著距離的增加，聲強將逐漸減弱。很多學者都對海底沉積物的吸收性質開展了理論研究和實際測量[13-19]，但是，目前還沒有學者針對地震波在海水中振幅的衰減規律開展研究。Bevc等[20-23]采用疊前深度域偏移方法來保證崎嶇海底成像并以此達到振幅補償的目的，但其崎嶇海底起伏范圍均為幾百米內，未達到深水勘探的1 000～3 000 m。Claerbout等[24-25]對海洋地震資料進行了衰減補償，但也未考慮不同介質的振幅衰減差異問題。

為了解決上述問題，筆者采用深水機器人、海水實驗室測量及深水VSP等多種方法定量測量了地震波在海水中的速度，明確了其分層特征，建立了分層模型，提出了在深水區特別是深水坡折帶地震資料

1 海水與海底沉積物聲學性質

1.1 水下機器人實測

2013年12月，在南海北部瓊東南盆地深水區首次利用水下機器人對海水進行了多次速度測量，最大測量水深1 500 m，并開展了系統的研究工作，得到如下認識：①深水區海水的速度具有明顯的三層結構（圖1-a），淺層（80 m以上）海水速度變化較小；②深度介于100～1 200 m，由于海水溫度逐漸降低（圖1-c），地震波在海水中的速度快速降低后逐漸降低到1 485 m/s；③1 200 m以下，海水溫度不再明顯降低，海水鹽度逐步控制了海水速度（圖1-b），鹽度升高，海水速度逐漸升高。海水聲學性質受多方面影響，具有明顯的分層成帶現象。

1.2 實驗室測定

實驗室測定海洋參數是海洋油氣資源研究的重要手段。筆者采用流體聲波測試儀測試不同靜水壓力下海水和海底沉積物的聲學性質，其承壓能力高達60 MPa，最高承受溫度為180 ℃。聲波速度采用透射法測量原理，縱波發射縱波接收，獲得如表1所示參數。實驗室成像結果顯示（圖1-d），雖然數值與海洋實測參數有所不同，但得到的規律與水下機器人的測量結果基本相同：①海水速度在水深0～800 m區域隨深度增加快速遞減；②水深800～1 500 m，海水速度隨深度增加而緩慢遞減；水深1 500～2 000 m，海水速度隨深度增加快速遞減；③水深大于2 000 m，海水速度則隨深度增加而快速遞增。淤泥速度在0～500 m水深區域隨水深增加而快速遞減，同時小于海水速度；在大于500 m水深區域，淤泥速度基本無變化，而在水深500～1 700 m，淤泥速度低于海水速度，超過1 700 m，淤泥速度則大于海水速度。

圖1 陵水深水區海水參數實測與實驗室測量結果圖

表1 實驗室測得的海水與海底沉積物聲學性質表

1.3 海水與地層衰減規律差異

為了更精確地測量地震波在海水中垂向傳播的球面擴散規律，定量研究在海水和地層兩種介質中地震波衰減規律的差異。除了實驗測定外，還在南海深水區開展了VSP測量。通過測量不同深度地震波的振幅，就可以直接擬合出其振幅的衰減規律。測量方法：將VSP測量儀器直接放入海水中，其依靠自身重力直接沉入水下。測量過程：儀器在進入海平面時對零，每隔50 m放炮，測量完畢時在海平面再次對零。通過疊加，噪聲得到了有效壓制，有效信息得到了增強。提取了每一個深度點的地震子波的均方根振幅，用指數函數A＝aRb進行擬合，其中A表示相對振幅，a、b表示衰減系數，R表示傳播距離。當擬合振幅衰減函數A＝1.0R－0.705，即a=1.0、b=－0.705（圖2），而以上述水體聲學物理特征結果正演的振幅衰減函數則為A=1.0R－0.66。

圖2 海水中地震波傳播距離和振幅的關系圖

海水可近似認為是均勻介質，經典的球面擴散理論預測的結果是A=1.0R－0.1。這與實際測量的結果并不吻合，表明海水的振幅衰減規律比球面擴散理論的預計要弱得多。

筆者從南海北部多個盆地挑選多口已鉆井的VSP資料進行處理和分析（表2中1井、2井、3井）。在波場分離的基礎上，提出了直達下行波的子波振幅，并對子波振幅進行歸一化處理，還去除了水深變化的因素，僅考慮在地層中傳播的振幅衰減問題。用指數函數A=aRb擬合測量數據，結果表明：在地層中衰減系數b介于1.8～2.3，而在海水中衰減系數b介于0.60～0.75（表2）。從表2中可以看出，海水和地層的振幅衰減規律存在巨大的差別，地震波傳播相同的距離，在海水中的振幅衰減比地層要弱很多。這個差異是目前深水地震振幅恢復技術沒有考慮的因素。

通常地層的振幅衰減規律變化不大，通過時變振幅恢復等辦法就可以解決不同地層的振幅衰減差異問題，但時變振幅恢復方法在大陸坡折帶地區的應用效果并不理想，主要原因在于海水和地層的振幅衰減規律差異大且突變。

從理論上講，單炮可以作為一個點震源產生的球面波場。經典的球面擴散理論認為：對于沒有衰減、均勻、水平層狀介質而言，地震波的能量衰減正比于1/r2（r為球面半徑），振幅隨傳播半徑的增大而減弱。一般而言，地震縱波速度隨深度增加，使地震波進一步發散，振幅衰減也隨距離的增加而加快。

表2 地震波的振幅衰減隨傳播距離的規律表

在地震波實際傳播過程中，振幅衰減機制卻是十分復雜的問題。地震波振幅衰減因素大體上可以分為5個因素[17]。筆者列舉和對比了這些因素在海水和地層兩種介質中的差異（表3）。不難得到結論，在海水和地層兩種介質中，地震波振幅衰減的因素存在差異。

表3 海水、地層兩種介質中地震波振幅的衰減因素差異表

2 深水地震資料解釋保真處理技術

2.1 變海水速度對深水資料深度偏移成像的影響

速度建模是深度偏移中非常關鍵的一步，速度模型的準確與否直接關系到深度偏移成像的好壞。PSDM是解決復雜地質體成像的有力工具，其成像的質量主要取決于所用的速度—深度模型的精度。在淺水區，海水深度橫向變化小，海水速度相對穩定，對下伏地層成像的影響很小，可以忽略。而當地震工區跨越淺水、坡折帶、深水地區時，海水深度的橫向快速變化導致速度場劇烈橫向變化，嚴重違背了疊前深度偏移方法對速度場的基本假設，成為影響地震偏移成像的關鍵因素。

海水速度隨著海底深度的變化而變化，在進行疊前深度偏移處理時，通常情況下海水速度給定常數值,若海底比較平坦，則對后期成像基本無影響。但如果海底是崎嶇變化的，水深變化比較大的情況下，會對下伏地層造成很大的影響，必須考慮海水速度隨水深的變化。對模型數據進行試算，結果表明：在崎嶇海底條件下，如果不考慮這種變化，直接用常速充填，會對下伏地層造成假構造。如圖3所示，圖3-b為在常數海水速度下，水平界面出現假的背斜構造特征（圖3-d圓圈部分），圖3-a將海水的分層特征信息轉化成平均層速度模型，其水平界面歸位準確。

將層狀海水速度應用到實際資料的處理中，從圖3中可以看出，相較于常數海水速度偏移剖面（圖3-f），層狀海水速度偏移效果（圖3-e）具有同相軸更為連續、信噪比更高的伏點，提高了整體成像分辨率與成像精度。

2.2 不同海水深度衰減對地震真振幅恢復的影響

在地震剖面上，地震響應的可信度取決于資料處理的保真度。在巖性勘探中，地震資料保真處理是關鍵[26-28]。只有最大限度將儲層物性的地震響應真實反映到地震剖面上，才能有效利用地震數據識別巖性儲層。保真地震資料處理主要包含：保持相對振幅關系、保護有效頻帶、保護地震低頻、保持地震相位。其中，保持相對振幅關系占有最重要的地位，是保真地震資料處理的核心。因此，地震資料的振幅恢復不僅是地震資料處理的重要課題，也直接影響了烴類檢測、儲層研究、聲波阻抗反演等很多課題。

2.2.1 球面擴散補償方法

依據射線理論Ursin等[29]給出的水平層狀、彈性介質下偏移距相關的球面擴散公式，并用泰勒級數展開。

在垂直入射時，地震波的振幅恢復函數D可以表示為：

其中

式中t表示雙程旅行時；表示速度平方的平均值；ti、vi分別表示第i層的時間和速度。

球面擴散恢復增益函數定義為:

式中v0表示對應時刻t0時的速度值。

如果不是零偏移距地震數據，對于水平層狀介質其球面擴散的公式為：

其中

式中X表示偏移距；θi表示第i層的入射角；di表示第i層的厚度。

圖3 變海水速度對深度偏移成像影響圖

在實際中，常用的公式還有Claerbout[24]提出的根據時間的恢復函數：

Claerbout[24]推薦a的取值為2。通常a的取值范圍介于1.6～2.2。

2.2.2 變參數振幅補償方法

筆者提出了變參數振幅補償方法，該方法充分考慮不同介質具有不同的振幅衰減規律。具體做法為：沿地震波傳播路徑將地下介質分成各小段，分別計算每一小段的旅行時間和補償系數，總的補償系數D就是各小段補償的乘積。

通常地，假設地下介質是水平層狀介質。把地下分為n層，每一個小層的厚度分別記做d1,d2, …,dn。地震波在每一小層的傳播路徑分別是r1,r2, …,rn。在垂直入射時，得到的振幅和傳播距離的關系：

其中

式中a1,a2, …,an表示每一段小層的補償系數。由于每一小層的補償系數是不一樣的，就可以妥善處理不同介質振幅衰減規律不一致的情況。

引入補償系數ai對每一個小層進行精細補償，并可控制海水和地層補償函數的界面。對于偏移距域的水平層狀介質，可以得到：

變參數補償主要針對水深變化大的區域，在相同旅行時情況下，其在海水和地層中的傳播距離并不一致，能量衰減和補償也不一樣，如圖4中的路徑1和路徑2就具有相同的旅行時。

路徑1、2的補償系數分別為：

由此即可有效消除因海水與地層具有不同衰減系數而帶來的地震資料保幅不一致的問題。

圖4 深淺水等時路徑補償差異示意圖

2.2.3 瓊東南坡折帶實際地震資料變參數振幅補償

圖5 坡折帶處地震資料圖

本文處理的地震資料來自南海北部大陸邊緣的瓊東南盆地，其海水深度介于150～3 000 m。從三維工區截取一條主測線可以看出（圖5-a），在純波剖面中，振幅以坡折帶為界，深淺水存在明顯差異：深水的海底反射明顯強于淺水；從T20～T50，淺水反射明顯強于深水反射。從純波剖面中提出了海底、T27兩層反射的振幅屬性更能說明這個問題（圖5-b），從圖中可以看出，分為淺水振幅屬性和深水振幅屬性兩個區域，兩個區域的振幅屬性完全不一樣，并且與坡折帶高度吻合。

圖6是采用不同振幅恢復方法得到的疊加剖面（沿海底拉平）。傳統補償方法的結果（圖6-b），淺水振幅明顯強于深水振幅，坡折帶兩側相同地層的振幅無法對比。變參數振幅補償方法的結果（圖6-c），深水和淺水的振幅在橫向上和垂向上更加均衡；同一反射層位可以從淺水區連續追蹤到深水區，振幅是連續、可靠的。由于淺水海底沉積物的反射系數大于深水沉積物的反射系數，所以淺水海底的反射應該強于深水海底反射。傳統方法補償后，淺水海底反射振幅弱于深水海底反射振幅，這主要是由于Newman補償函數帶來的過補償問題。在變參數振幅補償結果中，淺水區的海底反射是一個強反射，強于深水海底反射。所以，變參數振幅補償結果才是真實地下反射系數的表達。在CRP道集中，傳統方法補償結果在遠偏移距出現了強振幅異常問題（圖7-a）。變參數振幅補償的結果在偏移距方向的振幅均衡，AVO屬性更加合理，避免了遠偏移距的強振幅異常現象（圖7-b）。

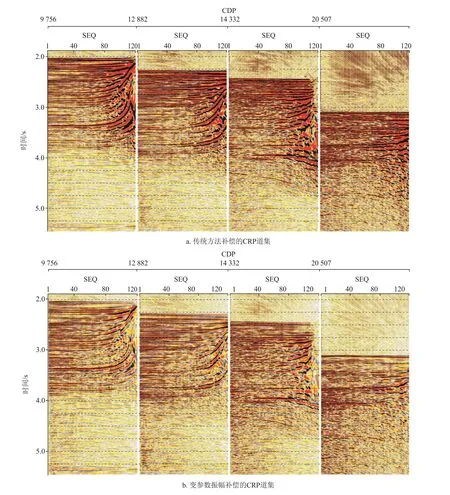
圖7 不同水深的CRP道集補償效果對比圖

3 深水區高保幅地震資料的應用

深水峽谷水道LSX10井區靠近峽谷水道壁，側封條件優越，具有較大的油氣勘探潛力，準確評價其物性與含氣性至關重要。常規AVO分析結果如圖8所示，從2個設計井點的AVO分析可以看出（圖8），該目標的G（梯度）屬性較小，振幅隨偏移距的微弱變化呈Ⅲ—Ⅳ類變化，從砂體頂界面原始AVO特征（圖9-a）和PXG屬性（圖9-c）可以看出，該砂體的AVO類型具有多變性。根據從變振幅恢復后AVO交匯圖（圖9-b）得出的含氣性指示因子（圖9-d），預測含氣邊界清晰、含氣范圍可靠；同時可以得到孔隙度指示因子（圖9-e），預測儲層物性好，砂體孔隙度預測為30%。在2020年部署LSX10探井，實鉆結果顯示鉆遇厚套氣層，孔隙度為32.1%，滲透率為861 mD，證實了海水聲學物理特征研究及基于其上的變參數振幅補償技術對于含氣性及孔隙度預測的有效性。

圖8 典型地震剖面及AVO變化規律特征圖

4 結論與建議

1）基于實際野外測量數據與實驗室測量數據融合，明晰海水與海底沉積物聲學特性隨水深變化呈現明顯分層性，同時考慮海水與地層衰減差異，針對水深變化區域，提出了變參數地震振幅恢復技術，有效解決了淺水—坡折帶—深水區域資料保幅性問題。

2）在瓊東南實際資料處理中，該方法補償的振幅更加均衡，同一反射地層可以連續追蹤；在偏移距方向，近、中、遠偏移距的地震振幅變化更加合理。保幅的地震信息為后續的儲層預測和烴檢奠定了重要的資料基礎。本研究成果在深水以及超深水等水深變化劇烈區帶勘探中具有重要的應用價值。

圖9 砂體頂界面AVO特征圖