兩種荷載對地下結構影響的對比分析

饒 飛，王國波

(武漢理工大學道路橋梁與結構工程湖北省重點實驗室,武漢 430070)

地下空間的應用在城市建設中變得越來越重要，許多城市的地下都建有地鐵車站、地下商場、停車場等地下結構，開發和利用地下空間已成為城市發展的熱點[1]。但地下結構在使用過程中也面臨著爆炸沖擊、碰撞沖擊等方面的威脅。因此，對于地下結構在爆炸荷載和強沖擊作用下的安全性分析和保護也成為研究的重點[2]。國內外許多學者分析了爆炸沖擊對地下結構的影響。蔡路軍等[3]利用DYNA模擬了上穿公路隧道油罐車偶然爆炸對下方供水隧洞穩定的影響，發現下方供水隧洞的拱頂、拱腰對爆炸沖擊波的響應較大，且拱頂、拱腰部位的最大振動速度大于水工隧洞的安全質點振動速度。孫金山等[4]結合鐵四院前大樓拆除工程，利用有限元軟件模擬了沙堤和減振溝對樓房拆除時塌落觸地沖擊的減振效果，結果發現多排小間距高沙堤可有效減少建筑物拆除時的塌落觸地振動。Koneshwaran等[5]分析了土體性質、土體覆蓋、爆炸距離等參數對隧道在爆破沖擊下破壞的影響，結果表明飽和土體中的隧道比埋在部分飽和或干燥土體中的隧道更容易受到嚴重破壞，這是由于埋在飽和土體中的隧道在爆炸沖擊下其周圍土體的有效正應力和剪切應力會減少，而部分飽和土體中的孔隙水起到了液體阻尼器的作用，另外發生在隧道中心正上方的地面爆炸更容易引起隧道的破壞。De等[6]研究了地表爆炸對地下結構的影響，分析了保護屏障的緩解作用，發現減振層的效果隨著厚度的增加而增加，但存在一個臨界厚度。Hassan等[7]研究了爆破荷載下保護屏障的作用，發現泡沫屏障對沖擊動荷載有很好的緩沖效果。Zhao等[8]提出了一種泡沫水泥基材料作為隧道的保護層，可有效減輕由爆破載荷引起的結構動態響應。

由上可見：許多學者對地下結構在爆炸沖擊下的響應進行了分析，并提出了有效的保護措施，同時現行地下結構設計相關規范也規定了地下結構設計時需要考慮的爆炸荷載，如《軌道交通工程人民防空設計規范》(RFJ 02-2009)[9]和《人民防空設計規范》(GB 50225-2005)[10]等。但是對于塌落觸地沖擊荷載對鄰近地下結構安全影響的研究十分匱乏，也未見相關規范對此進行說明。人防荷載和坍塌觸地沖擊荷載都屬于偶然荷載，作用時間短，消減快。但人防荷載本質上是在空氣中傳播的壓縮波作用于土體或結構上；而坍塌觸地沖擊荷載則是直接作用于土體的一種沖擊荷載，二者在本質上是不同的。因此，對于已考慮人防荷載而設計的地下結構在坍塌觸地沖擊荷載作用下是否會破壞尚需進一步深入探討。而荷載的確定是結構分析的基礎和前提，因此本文先側重介紹這兩類荷載，然后將二者進行對比分析。

1 人防荷載分析

根據有關人防荷載的相關規范[9,11]：地下結構在設計時需要考慮人防荷載。規范規定在進行地下結構設計時爆炸偶然荷載可采用等效靜荷載法來計算，并給出了常規武器及核武器在地表爆炸時所產生等效荷載的計算公式，人防武器在地表爆炸如圖1所示。

注：L1和L2分別為爆炸點到左側和右側頂板中心的水平距離，m；h、h1、h2為計算深度，m，計算頂板時，取頂板的覆土厚度h，計算外墻時，取防空地下室結構土中外墻中點至室外地面的深度h1、h2。圖1 人防武器地面爆炸Fig.1 Civil air defense ground explosion

1.1 軌道交通工程人民防空設計規范(常規武器)

地下結構頂蓋計算板塊上的均布等效靜荷載標準值可按式(1)～式(4)計算確定[9]：

p1=cakd1krph

(1)

(2)

(3)

(4)

式中：p1為地面常規武器爆炸下地下結構頂板均布等效靜載標準值，N/mm2；ca為土體拱效應系數；kd1為頂蓋計算板塊的動力系數；kr為頂蓋的綜合反射系數；ph為計算板塊中心處的土中壓縮波峰值壓力，MPa；h為頂蓋覆土厚度，m；△pi為常規武器在地面爆炸時所產生的空氣沖擊波的最大超壓，N/mm2；n為產生的沖擊在覆土介質中的衰減系數；C為等效TNT裝藥量，kg；Li為爆心至作用點的距離，m；ti為計算板塊中心處的地面沖擊波按等沖量簡化的等效作用時間，s。

1.2 人民防空地下室設計規范(常規武器)

常規武器地面爆炸作用下，地下結構頂板均布等效靜載標準值按式(5)與式(6)計算確定[11]：

p1=cekd1kr1ph

(5)

(6)

式中：ce為頂板荷載均布化系數；kr1為頂板綜合反射系數；v1為土的峰值壓力波速，m/s；δ為土的應變恢復比；η為修正系數。

文獻[9,11]中規定的防常規武器人防荷載隨結構埋深的變化如圖2所示。

圖2 常規武器人防荷載與結構埋深的關系Fig.2 The relationship between the load of conventional weapons and the buried depth of the structure

由圖2可見：文獻[9]規定的防常規武器人防荷載隨結構埋深的增加呈指數型衰減，文獻[11]規定的防常規武器人防荷載隨結構埋深呈線性衰減；文獻[9]規定的防常規武器人防荷載隨結構埋深增加而衰減的較快，隨著結構埋深增加，二者規定的防常規武器人防荷載接近，且此時的人防荷載都較小。

1.3 核武器

核武器爆炸作用下地下結構均布等效靜載標準值按式(7)與式(8)計算[9,11]：

p2=kd1kpdh

(7)

(8)

式中：p2為核武器爆炸作用下地下結構均布等效靜載標準值；△pm為空氣沖擊波超壓計算值，kN/m2；pdh為核武器在地面爆炸產生的土中壓縮波的最大壓力，kN/m2；k為頂板綜合反射系數；t2為地面空氣沖擊波按等沖量簡化的等效作用時間，s。

1.4 規范相關規定

文獻[9]給出了在地面常規武器和核武器爆炸下，一定覆土厚度的地下結構頂板在某些防抗級別下的等效靜載標準值，如表1和表2所示。

表1 常規武器作用地下結構均布頂板等效靜載標準值

表2 核武器作用下地下結構均布頂板等效靜荷載標準值

從表1和表2可以看出：防常規武器為5級和6級時，地面常規武器于地面爆炸時在地下結構頂板上產生的等效靜載不超過0.11 MPa，且隨著覆土厚度的增加頂板等效荷載逐漸減小，這是由于常規武器爆炸產生的壓縮波在土體中傳播時被消耗了，上部覆土對地下結構起到了保護作用；在防核武器中頂板等效靜載會隨著頂板區格最大短邊凈跨的增大而減小。

2 塌落觸地沖擊荷載分析

隨著拆除工程的增多，建筑物拆除時的塌落觸地影響逐漸引起了人們的關注，一些學者對塌落觸地的沖擊進行了分析，文獻[12]提出了基于Hertz定律的碰撞沖擊力模型，如式(9)～式(12)所示：

(9)

(10)

(11)

(12)

式中：p為碰撞沖擊力；n為接觸剛度系數；R為球形碰撞體或壓頭的半徑；a為變形位移；k為與材料有關參數；E為彈性模量；μ為泊松比；下標1和2分別代表碰撞體和被碰撞體。

在建筑物拆除塌落觸地的過程中，根據能量守恒可得：

(13)

式中：a1為最大形變位移；v為碰撞初始速度。

根據式(13)可得a1，再代入式(9)有：

(14)

把式(10) ～式 (12) 代入式(14)得：

(15)

根據Hertz方程可知，接觸區半徑a與沖擊力p的關系如式(16)所示，接觸區的壓力分布如式(17)所示：

(16)

(17)

式中：p0為接觸中心處的表面壓力；px,y為接觸區距接觸中心點(x,y)處的壓力。

對作用于接觸區的所有壓力求和，令總壓力等于p可得：

(18)

可得出接觸區和接觸中心壓力的方程為

(19)

(20)

將n的表達式代入式(20)得：

(21)

文獻[13]提出在強沖擊作用下，沖擊中心線下深度h處的壓力按式(22)計算：

(22)

式中：h為計算深度；ph為深度h處的壓力。

一般塌落體是被拆除的鋼筋混凝土結構，取其彈性模量為30 000 MPa，密度為2 500 kg/m3，泊松比為0.2。從上式可以看出當被拆建筑物材料確定以后，塌落觸地沖擊壓力主要與塌落體的質量、觸地速度和接觸半徑以及地面土體介質有關，地下結構所受的沖擊壓力主要與結構埋深有關，塌落觸地沖擊壓力隨各參數變化的定性關系如圖3所示。

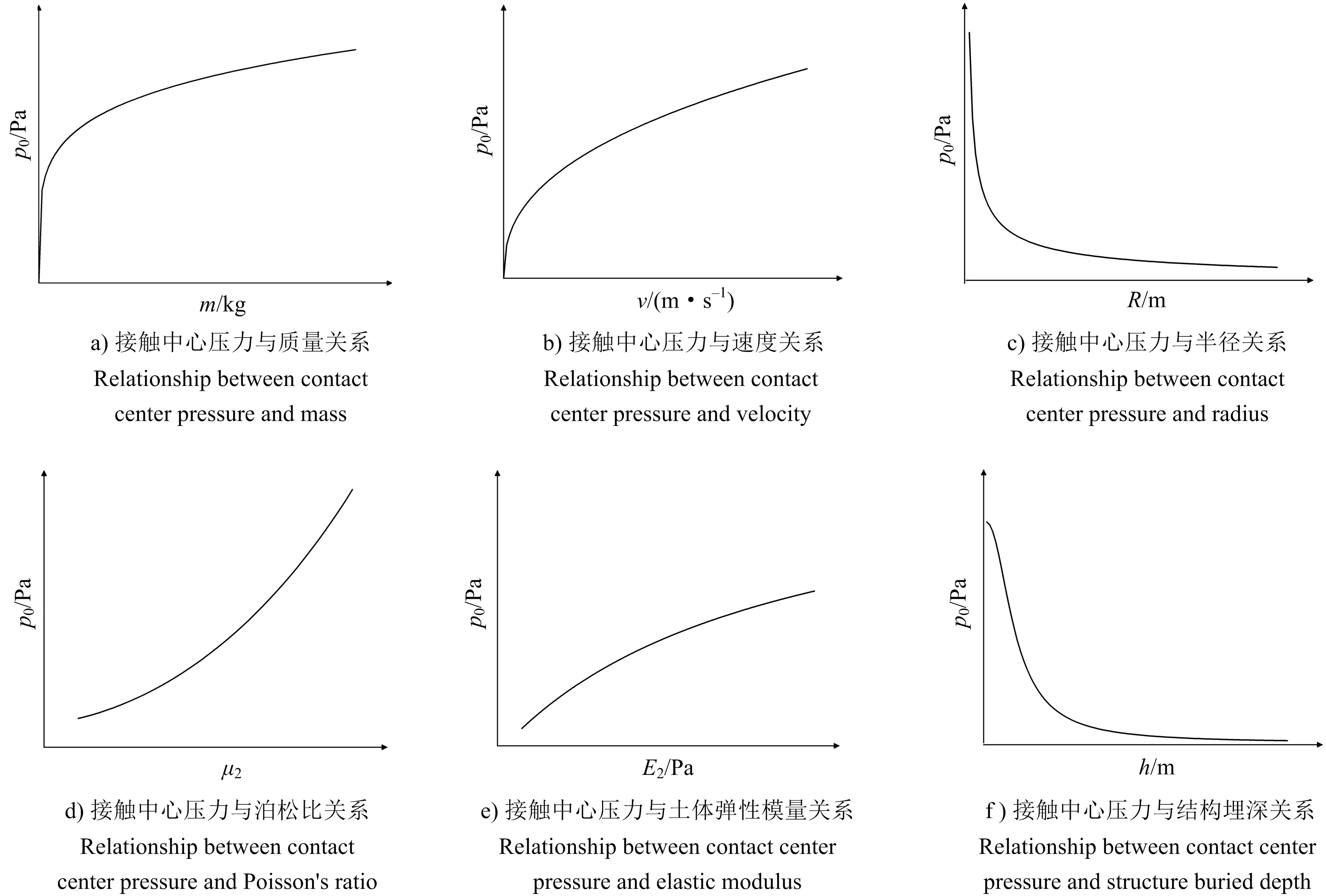
圖3 塌落觸地沖擊壓力與各參數關系Fig.3 Relationship between collapse impact pressure and various parameters

由圖3可見：

1)接觸中心的壓力隨觸地物體質量和速度的增加而增大，且在開始階段增長較快，超過一定值后增加速度又會變緩；

2)當質量、速度等其他條件一定時，觸地中心的沖擊壓力隨著塌落物體觸地半徑的增大而快速衰減，之后衰減速度又會降慢；

3)塌落觸地的沖擊壓力也會隨著地表土體彈性模量和泊松比的增加而增大，這是因為土體彈性模量越大，碰撞越趨近于彈性碰撞，損耗的能量也越少，沖擊壓力也會越大；

4)地表沖擊對地下結構的影響會隨著結構的埋深快速衰減，當結構埋深較小時，塌落觸地沖擊會對地下結構造成很大影響。

3 工程實例對比分析

3.1 實例計算

為對比分析人防荷載和坍塌觸地沖擊荷載作用下地下結構響應的大小，在此選取某矩形地鐵車站和圓形盾構隧道作為工程實例進行計算比較。

3.1.1 人防荷載計算

由于在人防荷載下，地下結構在頂板處受荷較大，因此這里僅計算地下結構頂板的情況。以某地鐵車站為例，其人防設計如表3和表4所示。

表3 某矩形地鐵車站頂板防常規武器設計

表4 某矩形地鐵車站頂板防核武器設計

再以某圓形隧道為例，該地區人防等級為5級，在進行隧道的人防設計時，由于隧道埋深為3 m大于2.5 m，由表1的注釋可知頂板可不考慮防常規武器的計算。其防核武器設計參數如表5所示。

表5 某圓形隧道防核武器設計

3.1.2 塌落觸地沖擊荷載計算

利用第2節討論的公式計算塌落觸地的沖擊荷載，假定塌落體為鋼筋混凝土結構，密度為2 500 kg/m3，標準工況為底面半徑0.5 m，高1 m的圓柱形混凝土結構以初速度為0從3 m的高度落下，計算結果如表6所示。

表6 塌落觸地荷載計算

由表6可見：

1)對比工況1和工況2可以看出塌落觸地最大沖擊壓力隨塌落物質量的增加而增大，地下結構所受的沖擊壓力隨地表沖擊壓力的增加而增大；

2)對比工況1和工況3可以看出塌落觸地最大沖擊壓力隨塌落高度的增加而增大；

3)對比工況1和工況4可以看出塌落觸地最大沖擊壓力隨初速度的增加而增大；

4)對比工況1和工況5可以看出，塌落觸地在地表處產生的最大沖擊壓力會隨著接觸半徑的減小而增大，但其對地下結構的影響會衰減的更快；

5)對比工況1和工況6可以看出塌落觸地沖擊壓力隨地面土體彈性模量的增加而增大；

6)對比ph1和ph2可以看出隨著結構埋深的增加，地表沖擊在地下結構上產生的影響會減小。

3.2 對比分析

人防荷載是壓縮波作用于土體，塌落觸地是直接作用于土體的沖擊荷載；在對比分析人防荷載和塌落觸地荷載時，先將兩種荷載在地表產生的壓力進行比較，然后將兩種荷載在地下結構上產生的等效荷載進行對比。人防荷載與塌落觸地沖擊荷載的對比如表7所示。由式(22)可知，當其他參數確定以后，地下結構所受壓力主要與接觸半徑和結構埋深有關，故在此只繪出了工況1和工況5兩種工況以及人防荷載下地下結構上的壓力隨結構埋深的變化曲線，兩種荷載在地下結構上產生的壓力與結構埋深關系如圖4所示。

表7 坍塌觸地荷載與人防荷載的對比

圖4 地下結構所受荷載與結構埋深的關系Fig.4 Relationship between the load on the underground structure and the buried depth of the structure

由表7和圖4可見：

1)塌落觸地沖擊在地表產生的荷載大于人防在地表處的荷載，坍塌觸地在矩形車站和圓形隧道上產生的荷載也大于相應的人防荷載；

2)塌落觸地沖擊在地下結構上產生的荷載隨結構埋深的增加而減小，人防荷載隨結構埋深變化不明顯；

3)當結構埋深較小時，坍塌觸地沖擊在地下結構上產生的壓力是遠大于相應的人防荷載的，當地下結構埋深達到一定深度時，人防荷載和坍塌觸地沖擊荷載在地下結構上產生的壓力接近，但此時的值很小，對地下結構的影響也較小。

4 結語

1)塌落觸地沖擊壓力隨塌落體質量、塌落體初速度、地面土體彈性模量和泊松比的增加而增大；隨接觸半徑的增大而減小。

2)塌落觸地沖擊在地下結構上產生的壓力隨結構埋深的增加而衰減，且當接觸半徑較小時，衰減的更快。

3)在所選取的塌落觸地工況下，當結構埋深較小時，塌落觸地在地下結構上產生的荷載遠大于地下結構設計時考慮的人防荷載；且所選取的工況是偏于保守的，而實際的塌落體質量、塌落體初速度等會更大，對地下結構產生的影響也會更大，因此在建筑物拆除時鄰近若有地下結構需要考慮塌落觸地沖擊壓力對地下結構的影響。